머리말:

이번 호에서는 접두어와 알고리즘에 대해 알아보도록 하겠습니다! ! !

1. [템플릿] 접두사 및

2. [템플릿] 2차원 접두어 합

3. K로 나눌 수 있는 하위 배열을 합산합니다.

요약하다

(1) 접두사 합 알고리즘이란 무엇입니까?

접두어 합 알고리즘은 배열의 접두어 합을 효율적으로 계산하기 위한 알고리즘 입니다 . 접두사 sum은 배열의 시작 위치부터 특정 위치까지의 모든 요소의 합을 나타냅니다 .

다음은 접두사 합계 알고리즘의 기본 단계입니다.

원래 배열과 동일한 길이의 접두사 합계 배열을 만듭니다. 처음에는 접두사 합계 배열의 첫 번째 요소가 원래 배열의 첫 번째 요소와 동일합니다.
두 번째 요소부터 시작하여 원래 배열을 순회하고 각 위치의 접두사 합계를 계산합니다. 즉, 이전 위치의 접두사 합계를 현재 위치의 요소에 추가합니다.
계산된 접두사 합계를 접두사 합계 배열의 해당 위치에 저장합니다.
순회가 완료된 후 원래 배열의 각 위치에 대한 접두사와 값이 접두사와 배열에 저장됩니다.

접두사 합 알고리즘의 가장 큰 장점은 매번 계산을 다시 순회할 필요 없이 O(n)의 낮은 시간 복잡도로 지정된 범위에 있는 요소의 합을 계산할 수 있다는 것입니다.

다음은 접두사 합계 알고리즘을 사용하여 배열의 접두사 합계를 계산하는 방법을 보여주는 예입니다.

원래 배열: [1, 2, 3, 4, 5]
접두사 합계 배열: [1, 3, 6, 10, 15]

【설명하다】

원래 배열의 접두사 합계: [1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5] = [1, 3, 6, 10, 15]

(2) 주제 설명

1. [템플릿] 접두사 및

링크는 다음과 같습니다 . [템플릿] 접두사 및

[알고리즘 아이디어]

a. 먼저 "접두사 합계" 배열을 전처리합니다.

dp[i]를 사용하여 다음을 나타냅니다. [1, i] 구간에 있는 모든 요소의 합, dp[i - 1]에 저장되는 내용은 구간 [1, i-1]에 있는 모든 요소의 합입니다. 그러면 다음과 같은 재귀 공식을 얻을 수 있습니다: dp[i] = dp[i - 1] + arr[i]

b. "특정 간격으로" 모든 요소의 합을 "빠르게" 찾으려면 접두사와 배열을 사용합니다.

쿼리된 간격이 [l, r]인 경우: 간격에 있는 모든 요소의 합계는 dp[r] - dp[l - 1] 입니다.

[코드 표시]

#include <iostream>
using namespace std;

const int N = 100010;
long long arr[N], dp[N];
int n, q;

int main()
{
    cin >> n >> q;
    // 读取数据
    for(int i = 1; i <= n; i++) cin >> arr[i];
    // 处理前缀和数组
    for(int i = 1; i <= n; i++) dp[i] = dp[i - 1] + arr[i];
    while(q--)
    {
        int l, r;
        cin >> l >> r;
        // 计算区间和
        cout << dp[r] - dp[l - 1] << endl;
    }
    return 0;
}

출력 표시:

【성능 분석】

시간 복잡도:

접두어 합계 배열 초기화: 전체 원래 배열을 순회해야 하며 시간 복잡도는 O(n)입니다.
각 쿼리에 대한 간격 합계를 계산합니다. 일정한 수의 작업만 필요하며 시간 복잡도는 O(1)입니다.
전체 시간 복잡도는 O(n + q)입니다. 여기서 n은 배열 길이를 나타내고 q는 쿼리 수를 나타냅니다.

공간 복잡도:

공간 복잡도는 O(n)입니다. 여기서 n은 배열 길이를 나타냅니다. 계산된 접두사 합계를 저장하려면 추가 접두사 합계 배열이 필요합니다.

【알아채다】

여기에 자세한 질문이 있습니다. 아래 첨자가 0부터 시작하지 않고 1부터 시작하는 이유는 무엇입니까?

사실 매우 간단한데, 이 코드에서 배열 인덱스가 1부터 시작하는 이유는 접두어 합 계산을 용이하게 하기 위함입니다.

접두사 합계 알고리즘에서는 각 요소가 처음부터 현재 위치까지 원래 배열의 누적 합계를 나타내는 접두사 합계 배열을 유지해야 합니다.
배열 인덱스가 0부터 시작하는 경우 접두사 합을 계산할 때 인덱스가 0인 경우를 특별히 처리해야 하므로 코드가 복잡해집니다.

배열 인덱스를 1부터 시작하면 접두어 합계 계산 논리를 더 간단하고 직관적으로 만들 수 있습니다. 예를 들어, i번째 위치의 접두어 합은 dp[i] = dp[i-1] + arr[i]인덱스 0인 경우를 추가로 처리하지 않고도 로 계산할 수 있습니다.

2. [템플릿] 2차원 접두어 합

링크는 다음과 같습니다 . [템플릿] 2차원 접두어 합

[알고리즘 아이디어]

1차원 배열의 형태와 유사하게 [0, 0] 위치부터 [i, j] 위치까지의 영역에 있는 모든 요소의 누적합을 처리할 수 있다면 O(1)에서 처리할 수 있습니다. 시간 행렬의 모든 영역에 있는 모든 요소의 누적 합계입니다. 따라서 다음 두 단계만 완료하면 됩니다.

1단계 : 접두사 및 행렬 가져오기

여기서는 1차원 배열에 대한 확장된 지식을 활용해야 하는데, 행렬의 상단과 왼쪽에 0의 행과 열을 추가해야 하므로 많은 경계 조건의 처리를 절약할 수 있습니다(동창 우리 접두사와 행렬을 스스로 생각해내려고 시도할 수 있지만 경계 조건을 처리하면 무너질 것입니다. 처리된 행렬은 다음과 같습니다.

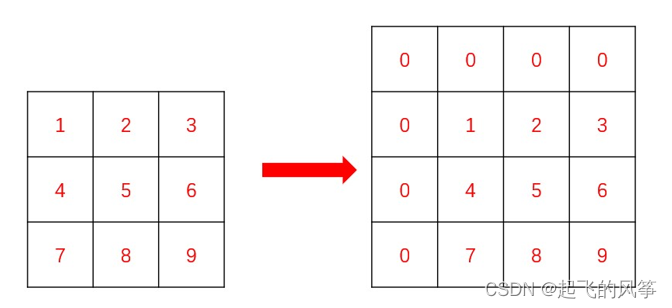
이런 식으로 접두사와 행렬 배열을 채울 때 첨자는 1부터 바로 시작하는데, i - 1 과 j - 1 위치의 값을 과감하게 사용할 수 있다 .

dp 테이블과 원래 배열 행렬의 요소 간의 매핑 관계에 유의하세요.

i. dp 테이블에서 행렬 행렬까지 수평 및 수직 좌표를 1만큼 줄입니다.
ii. 행렬 행렬에서 dp 테이블까지 가로 및 세로 좌표에 1을 추가합니다.

접두합 행렬에서 sum[i][j]의 의미와 2차원 접두합 방정식을 재귀적으로 사용하는 방법

a. sum[i][j]의 의미:

sum[i][j]는 [0, 0] 위치에서 [i, j] 위치까지의 영역에 있는 모든 요소의 누적 합계를 나타냅니다. 아래 그림의 빨간색 영역에 해당합니다.

b. 재귀 방정식:

사실 이 재귀 방정식은 초등학교에서 그래프의 넓이를 구하던 문제와 매우 유사하며, 그 넓이를 [0, 0] 위치에서 [i, j] 위치로 분해하면 다음 부분:

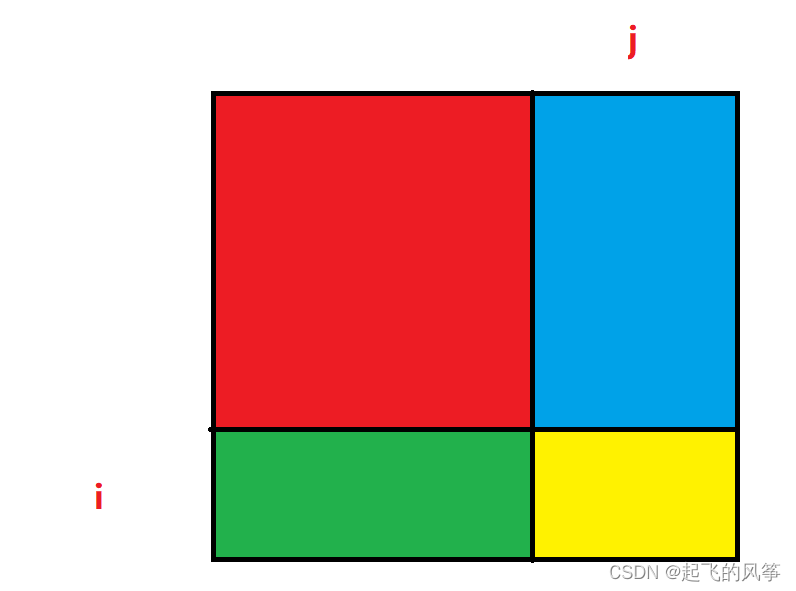
sum[i][j] = 빨간색+파란색+녹색+노란색, 다음 네 가지 영역을 분석합니다.

i. 노란색 부분이 가장 간단하며 배열의 행렬[i - 1][j - 1]입니다(좌표의 매핑 관계에 유의하세요).
ii. 단일 파란색을 찾는 것은 어렵습니다. 이는 우리가 정의한 상태 표현의 영역이 아니기 때문이고 마찬가지로 단일 녹색도 마찬가지입니다.
iii.하지만 빨간색 + 파란색인 경우 dp 배열의 sum[i - 1][j] 값이 됩니다.
iv. 마찬가지로 빨간색 + 녹색이면 dp 배열의 sum[i][j - 1] 값이 됩니다.
v. 위에서 계산한 3가지 값을 더하면 흰색+빨간색+파란색+빨간색+녹색이 되는데, 빨간색의 면적이 과대계산된 것을 발견하여 의 면적을 빼면 된다. 빨간색은 별도로;
vi. 빨간색 영역은 dp 배열의 정의, 즉 sum[i - 1][j - 1] 과 정확히 일치합니다.

요약하면 재귀 방정식은 다음과 같습니다.

sum[i][j]=sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j -1]+matrix[i - 1][j - 1]

2단계 : 접두어 합 행렬 사용

제목의 인터페이스에 제공된 매개변수는 원본 행렬의 첨자입니다. 첨자 매핑 오류를 방지하기 위해 첨자는 dp 테이블의 해당 첨자에 직접 매핑됩니다: row1++, col1++, row2++, col2++

다음으로, 아래와 같이 이 접두사 합계 행렬을 사용하는 방법을 분석합니다(여기서 행과 열은 합계 행렬의 아래 첨자에 따라 처리되었습니다).

왼쪽 위 모서리(row1, col1)와 오른쪽 아래 모서리(row2, col2)로 둘러싸인 영역의 경우 빨간색 부분이 발생합니다. 따라서
우리에게 필요한 것은 빨간색 부분의 면적이며, 우리는 계속해서 여러 영역을 분석할 것입니다:

i. 노란색은 직접 계산할 수 있는데, 합[row1 - 1, col1 - 1] 입니다. (왜 1씩 줄이나요? 행 행과 열 열을 제거해야 하기 때문에)
ii.녹색은 직접 찾기는 어렵지만 노란색과 결합하면 합 테이블의 sum[row1 - 1][col2]의 데이터가 된다.
iii. 마찬가지로 파란색은 찾기 어렵지만 파란색 + 노란색 = sum[row2][col1 - 1];
iv. 전체 지역을 살펴보겠습니다. 찾기 쉽나요? 찾기가 매우 쉽습니다. sum[row2][col2];
v. 그러면 빨간색 = 전체 영역 - 노란색 - 녹색 - 파란색이지만 녹색과 파란색은 찾기 어렵습니다. 전체 영역 - (녹색 + 노란색) - (파란색 + 노란색)과 같이 뺄 수 있습니다. 많은 것과 동일합니다. 하나를 빼고 더하세요.

요약하자면: 빨간색 = 전체 영역 - (녹색 + o) - (파란색 + o) + o이므로 빨간색 영역에 있는 요소의 합은 다음과 같이 얻을 수 있습니다.

sum[row2][col2]-sum[row2][col1 - 1]-sum[row1 - 1][col2]+sum[row1 -1][col1 - 1]

[코드 표시]

#include <iostream>
using namespace std;

const int N=1010;
int arr[N][N];
long long dp[N][N];
int n,m,q;

int main() 
{
    cin >> n >>m >>q;

    // 读⼊数据
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++){
            cin >> arr[i][j];
        }
    }
    // 处理前缀和矩阵
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j -1];
        }  
    }
    
    // 使⽤前缀和矩阵
    int x1, y1, x2, y2;
    while(q--)
    {
        cin >>x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 -1] << endl;
    }
    return 0;
}
// 64 位输出请用 printf("%lld")

출력 표시:

【성능 분석】

시간 복잡도:

접두합 행렬 초기화: 원본 행렬 전체를 순회해야 하며 시간 복잡도는 O(n * m)입니다. 여기서 n은 행 수, m은 열 수를 나타냅니다.
각 쿼리에 대한 면적 합계를 계산합니다. 일정한 수의 작업만 필요하며 시간 복잡도는 O(1)입니다.
전체 시간 복잡도는 O(n * m + q)입니다. 여기서 n은 행 수, m은 열 수, q는 쿼리 수를 나타냅니다.

공간 복잡도:

공간 복잡도는 O(n * m)입니다. 여기서 n은 행 수를 나타내고 m은 열 수를 나타냅니다. 계산된 접두어 합을 저장하려면 추가적인 접두어 합 행렬이 필요합니다.

3. K로 나눌 수 있는 하위 배열을 합산합니다.

링크는 다음과 같습니다 . K로 나눌 수 있는 하위 배열

[해결책] (무차별 대입 솔루션은 모든 하위 배열의 합계를 계산하는 것이므로 여기서는 자세히 설명하지 않겠습니다.)

이 질문에 필요한 전제 지식:

동여 정리

(a - b) % n == 0이면 a % n == b % n이라는 결론을 얻을 수 있습니다. 말로 설명하자면, 두 숫자의 차이가 n으로 나누어지면 두 숫자의 모듈로 n의 결과는 동일합니다.

예: (26 - 2) % 12 == 0, 26 % 12 == 2 % 12 == 2

C++에서 음수 모듈로의 결과 및 "음수 모듈로"의 결과를 수정하는 방법

a.C++에서 음수의 모듈로 연산과 관련하여 결과는 "음수를 양수로 처리하고 모듈로 결과에 음수 부호를 추가합니다."입니다. 예: -1 % 3 = -(1 % 3) = -1
b.음수가 있으므로 "음수"의 발생을 방지하기 위해 (a % n + n) % n 형식의 출력은 양수를 보장합니다.

예: -1 % 3 = (-1 % 3 + 3) % 3 = 2

[알고리즘 아이디어]

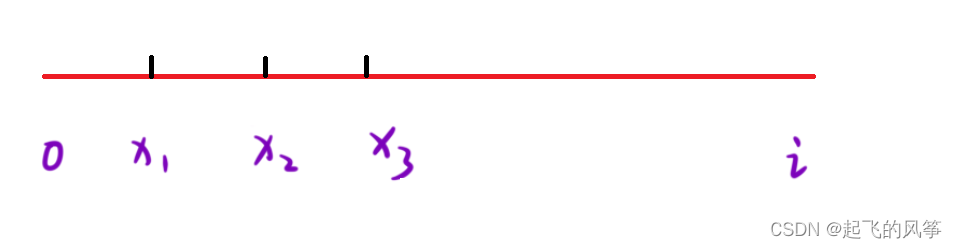
i를 배열의 임의의 위치로 두고 sum[i]를 사용하여 간격 [0, i]에 있는 모든 요소의 합을 나타냅니다.

1. "i로 끝나고 k로 나누어지는 하위 배열"의 수를 알고 싶다면 간격 [x, i의 모든 배열이 x1, x2, x3...이 되는 시작 위치 수를 찾아야 합니다. ] 요소의 합은 k로 나누어집니다.
2. 구간 [0, x - 1]에 있는 모든 요소의 합이 a와 같고, 구간 [0, i]에 있는 모든 요소의 합이 b와 같다고 가정하면 (b - a를 얻을 수 있습니다. ) %k == 0
.
3. 합동 정리에 따르면 구간 [0, x - 1]의 접두어 합은 구간 [0, i]와 일치합니다. 따라서 질문은 다음과 같습니다.

간격 [0, i - 1]에서 나머지가 sum[i] % k와 동일한 접두어 합계의 수를 알아보세요.

접두사와 배열을 초기화할 필요는 없습니다. 왜냐하면 위치 i 이전에 접두사와 합계가 sum[i] - k인 수에만 관심이 있기 때문입니다. 따라서 해시 테이블을 이용하여 현재 위치의 접두어 합계를 구하고 동시에 각 접두어 합계의 발생 횟수를 저장하면 됩니다.

[코드 표시]

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int, int> tmp;
        tmp[0 % k] = 1; // 0 这个数的余数
        int sum = 0;
        int res = 0;
        for(auto x : nums)
        {
            sum += x; // 算出当前位置的前缀和
            int r = (sum % k + k) % k; // 修正后的余数
            if(tmp.count(r)) 
                res += tmp[r]; // 统计结果
            tmp[r]++;
        }
    return res;
    }
};

[출력 표시]

【성능 분석】

시간 복잡도:

원래 배열을 순회하고 접두사 합계를 계산합니다. 원래 배열은 한 번 순회해야 하며 시간 복잡도는 O(n)입니다. 여기서 n은 원래 배열의 길이를 나타냅니다.
각 위치에서 해시 테이블을 업데이트하고 결과를 계산합니다. 각 요소에 대해 접두어 합계를 계산하고 해시 테이블 작업을 수행하고 결과를 계산하는 데 일정한 시간만 걸립니다. 전체 시간 복잡도는 O(n)입니다.

공간 복잡도:

공간 복잡도는 O(n)입니다. 여기서 n은 원래 배열의 길이를 나타냅니다. 주로 접두어 합계를 저장하는 데 사용되는 해시 테이블입니다.

요약하다

접두어 합 알고리즘은 문제 해결의 효율성을 향상시킬 수 있는 중요하고 실용적인 알고리즘입니다. 접두사와 알고리즘의 원리와 응용을 익힌 후에는 이를 다양한 문제에 유연하게 활용하여 알고리즘의 효율성을 높일 수 있습니다.

[선호 알고리즘] - 접두사 합계 알고리즘

(1) 접두사 합 알고리즘이란 무엇입니까?

(2) 주제 설명

1. [템플릿] 접두사 및

2. [템플릿] 2차원 접두어 합

3. K로 나눌 수 있는 하위 배열을 합산합니다.

요약하다

Supongo que te gusta