Optimización: Modelado, Algoritmos y Teoría
Actualmente estoy estudiando el libro Optimización: Modelado, Algoritmos y Teoría. Lo registraré aquí y tomaré algunas notas. También agregaré algo de mi propio conocimiento y trataré de no escribir de una manera tan rígida (por supuesto, la más básico Todavía tengo que tenerlo)
El texto completo tiene 28,365 palabras, por lo que es agotador
Capítulo 2 Conocimientos básicos
2.1 Norma
2.1.1 Norma vectorial
Definición 2.1 (Norma) Una función no negativa ||·|| del espacio vectorial R n al campo de números reales R se llama norma si satisface:
(1) Definitividad positiva: para todo v ∈ R nv{\in }R^nv ∈ Rn,有∣ ∣ v ∣ ∣ > = 0 ||v|| >= 0∣∣v ∣∣ _>=0 , y∣ ∣ v ∣ ∣ = 0 ||v|| = 0∣∣v ∣∣ _=0 si y sólo siv = 0 v=0v=0
(2) Homogeneidad: para todov ∈ R nv{\in}R^nv ∈ Rn和α ∈ R {\alpha}{\in}Rα ∈ R , hay∣ ∣ α v ∣ ∣ ||{\alpha}v||∣∣ α v ∣∣ =∣ α ∣ |{\alpha}|∣ α ∣ ∣ ∣ v ∣ ∣ ||v||∣∣ v ∣∣
(3) Desigualdad triangular: Para todov , w ∈ R nv,w{\in}R^nv ,w∈R _ _n ,有∣ ∣ v + w ∣ ∣ < = ∣ ∣ v ∣ ∣ + ∣ ∣ w ∣ ∣ ||v+w|| <= ||v|| + ||w||∣∣v _+w∣∣ _<=∣∣v ∣∣ _+∣∣ w ∣∣La
norma vectorial más comúnmente utilizada es lpnorma (p >= 1)
∣ ∣ v ∣ ∣ p = ( ∣ v 1 ∣ p + ∣ v 2 ∣ p + … + ∣ vn ∣ p ) 1 / p ||v||_{p} = (|v_{1}|^p + |v_{2}|^p + \ldots + |v_{n}|^p)^{1/p}∣∣ v ∣ ∣p=( ∣v _1∣p+∣v2∣p+…+∣vn∣p)1/p
显而易见,高数应该都学过,如果 p = ∞ p={\infty} p=∞,那么 l ∞ l_\infty l∞范数定义为 ∣ ∣ v ∣ ∣ ∞ = m a x ∣ v i ∣ ||v||_\infty = max|v_i| ∣∣v∣∣∞=max∣vi∣
记住 p = 1 , 2 , ∞ p = 1,2,{\infty} p=1,2,∞的时候最重要,有时候我们会忽略 l 2 l_2 l2范数的角标
也会遇到由正定矩阵 A A A诱导的范数,即 ∣ ∣ x ∣ ∣ A = x T A x ||x||_A = \sqrt{x^TAx} ∣∣x∣∣A=ximpuestos __
para l 2 l_2yo2Norma, existe la desigualdad de Cauchy comúnmente utilizada, sea a, b ∈ R na,b{\in}R^nun ,segundo ∈ Rn,则
∣ a T b ∣ < = ∣ ∣ a ∣ ∣ 2 ∣ ∣ b ∣ ∣ 2 |a^Tb|<=||a||_2||b||_2∣ unT segundo∣<=∣∣ un ∣ ∣2∣∣ b ∣ ∣2
El signo igual se cumple si y sólo si a está linealmente relacionado con b
2.1.2 Norma matricial
La norma matricial primero debe satisfacer las mismas tres características, es decir, debe satisfacer certeza positiva, homogeneidad y desigualdad triangular . Las más utilizadas son l 1, l 2 l_1, l_2yo1,yo2norma, cuando p = 1 p = 1pag=Cuando 1 , matriz A ∈ R m ∗ n A{\in}R^{m*n}Un ∈ Rm∗n的范数定义
∣ ∣ A ∣ ∣ 1 = ∑ i = 1 m ∑ j = 1 n ∣ a i j ∣ ||A||_1={\sum_{i=1}^m}{\sum_{j=1}^n}|a_{ij}| ∣∣A∣∣1=i=1∑mj=1∑n∣aij∣
当 p = 2 p=2 p=2时,也叫矩阵的Frobenius范数(F范数),记为 ∣ ∣ A ∣ ∣ F ||A||_F ∣∣A∣∣F,其实就是所有元素的平方和然后开根号,具体定义如下
∣ ∣ A ∣ ∣ F = T r ( A A T ) = ∑ i , j a i j 2 ||A||_F=\sqrt{Tr(AA^T)}=\sqrt{\sum_{i,j}a_{ij}^2} ∣∣A∣∣F=Tr(AAT)=i,j∑aij2
T r Tr aquíT r representa la traza de la matriz cuadrada. La suma de cada elemento en la recta se llama traza (o número de traza) de la matriz A, generalmente denotada como tr(A)), y la norma F de la matriz tiene ortogonalidad. invariancia.
La invariancia ortogonal significa que para matrices ortogonalesU ∈ R m ∗ n , V ∈ R m ∗ n U{\in}R^{m*n},V{\in}R^{m*n}U ∈ Rmetro ∗ norte ,V∈R _ _m ∗ n , tenemos
∣ ∣ UAF ∣ ∣ F 2 = ∣ ∣ A ∣ ∣ F 2 ||UAF||_F^2=||A||_F^2∣∣ U A F ∣ ∣F2=∣∣A∣∣ _ _ _F2
No escribiré la derivación específica aquí, es demasiado problemático escribir la fórmula jaja, si estás interesado, puedes leer la página 24 de este libro o venir a verme ^^
矩阵范数也可以由向量范数给诱导出来,一般称这种算数为诱导范数,感觉用的不是很多,这里先不扩展开了
除了上诉的1范数,2范数,另一个常用的矩阵范数是核范数,给定矩阵 A ∈ R m ∗ n A{\in}R^{m*n} A∈Rm∗n,核范数定义为
∣ ∣ A ∣ ∣ ∗ = ∑ i = 1 r σ i ||A||_*=\sum_{i=1}^r{\sigma}_i ∣∣A∣∣∗=i=1∑rσi
其中 σ i , i = 1 , 2 , . . . , r {\sigma}_i,i=1,2,...,r σi,i=1,2,...,r为 A A A的所有非0奇异值, r = r a n k ( A ) r=rank(A) r=rank(A),类似于向量的 l 1 l_1 l1范数可以保稀疏性,我们也通常通过限制矩阵的核范数来保证矩阵的低秩性。
2.1.3 矩阵内积
内积一般用来表征两个矩阵之间的夹角,一个常用的内积—Frobenius内积, m ∗ n m*n m∗n的矩阵 A A A和 B B B的Frobenius内积定义为
< A , B > = T r ( A B T ) = ∑ i = 1 m ∑ j = 1 n a i j b i j <A,B>=Tr(AB^T)=\sum_{i=1}^m\sum_{j=1}^na_{ij}b_{ij} <A,B>=Tr(ABT)=i=1∑mj=1∑naijbij
De hecho, es la multiplicación de elementos correspondientes uno a uno de dos matrices.
De manera similar, también tenemos la desigualdad de Cauchy correspondiente a la norma matricial. Sea A, B ∈ R m ∗ n A,B{\in}R ^{m*n}un ,segundo ∈ rm ∗ n,则
∣ < A , B > ∣ < = ∣ ∣ A ∣ ∣ F ∣ ∣ B ∣ ∣ F |<A,B>|<=||A||_F||B||_F∣<un ,B>∣<=∣∣A∣∣ _ _ _F∣∣ B ∣ ∣F
El signo igual se cumple si y sólo si A y B están relacionados linealmente
2.2 Derivados
2.2.1 Matriz de gradiente y Hessor
La definición de gradiente (esto debería ser algo que nunca haya visto antes): función dada f: R n → R f:R^n{\rightarrow}RF:Rnorte →R, yfff en el puntoxxEs significativo dentro de una vecindad de x , si hay un vector g ∈ R ng{\in}R^ngramo ∈ Rn满足
lim p → 0 f ( x + p ) − f ( x ) − g T p ∣ ∣ p ∣ ∣ = 0 \lim_{p{\rightarrow}0}\frac{f(x+p)-f(x)-g^Tp}{||p||}=0 p→0lim∣∣p∣∣f(x+p)−f(x)−gTp=0
就称 f f f在点 x x x处可微,此时 g g g称为 f f f在点 x x x处的梯度,记作 ∇ f ( x ) {\nabla}f(x) ∇f(x),如果对区域D上的每一个点 x x x都有 ∇ f ( x ) {\nabla}f(x) ∇ f ( x ) existe, entonces se llamafff es diferenciable en D
Luego, después de una serie de derivaciones, podemos obtener la conocida fórmula de gradiente
∇ f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , . . . , ∂ f ( x ) ∂ xm ] T {\nabla}f(x)=\left[ \begin{matrix} {\frac{ {
\partial}f(x)}{
{\partial}x_1}} , {\frac{
{\partial} f(x)}{
{\partial}x_2}} ,...,{\frac{
{\partial}f(x)}{
{\partial}x_m}} \end{matrix} \right ]^T∇f ( x ) _=[∂ x1∂f ( x ) _,∂ x2∂f ( x ) _, ... ,∂ xm∂f ( x ) _]TPara
una función multivariada, podemos definir su matriz de Hessor: si funciónf ( x ) : R n → R f(x):R^n{\rightarrow}Rf ( x ):Rn →Ren el puntoxxDerivada parcial de segundo orden en x ∂ 2 f ( x ) ∂ xi ∂ xji , j = 1 , 2 , . . . , n \frac{ { \
partial}^2f(x)}{
{\partial}x_i{\ parcial}x_j}i,j=1,2,...,n∂ xyo∂ xj∂2f (x)_yo ,j=1 ,2 ,... ,n都存在,则
∇ 2 f ( x ) = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x 1 ∂ xn ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 ⋯ ∂ 2 f ( x ) ∂ x 2 ∂ xn ⋮ ⋮ ⋮ ∂ 2 f ( x ) ∂ xn ∂ x 1 ∂ 2 f ( x ) ∂ xn ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ xn 2 ] {\nabla}^2f(x)=\left[ \begin{matrix} \frac{ {\partial}^2f(x)}
{
{ \partial}x_1^2} & \frac{
{\partial}^2f(x)}{
{\partial}x_1{\partial}x_2} & \cdots& \frac{ {
\partial}^2f(x)}{
{\partial}x_1{\partial}x_n}\\ \frac{ {
\partial}^2f(x)}{
{\partial}x_2{\partial}x_1} &\frac{ {
\partial}^2f(x )}{
{\partial}x_2^2} & \cdots & \frac{
{\partial}^2f(x)}{
{\partial}x_2{\partial}x_n} \\ \vdots & \vdots & &\vdots\\ \frac{ {
\partial}^2f(x)}{
{\partial}x_n{\partial}x_1} & \frac{
{\partial}^2f(x)}{
{\partial}x_n{\partial}x_2} & \cdots &\frac{ {
\partial}^2f(x)}{
{\partial}x_n^2 } \end{matriz} \right]∇2f (x)_=
∂ x12∂2f (x)_∂ x2∂ x1∂2f (x)_⋮∂ xnorte∂ x1∂2f (x)_∂ x1∂ x2∂2f (x)_∂ x22∂2f (x)_⋮∂ xnorte∂ x2∂2f (x)_⋯⋯⋯∂ x1∂ xnorte∂2f (x)_∂ x2∂ xnorte∂2f (x)_⋮∂ xnorte2∂2f (x)_
convertirse en fff en el puntoxxMatriz de arpillera en x
cuando∇ 2 f ( x ) {\nabla}^2f(x)∇2 f(x)xxdel área DSi x existe, se llamafff es diferenciable de segundo orden en D. Si es continua en D, se puede demostrar que la matriz de Hesse en este momento es una matriz simétrica.
Cuandof: R n → R mf:R^n{\rightarrow}R^ metroF:Rnorte →RCuando m es una función con valores vectoriales, podemos definir su matriz jacobianaJ ( x ) ∈ R m ∗ n J(x){\in}R^{m*n}J ( x ) ∈ Rm ∗ n , su componente de la i-ésima filafi ( x ) f_i(x)Fyo( x )梯度的转置,即
J ( x ) = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ⋯ ∂ f 1 ( x ) ∂ xn ∂ f 2 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 2 ⋯ ∂ f 2 ( x ) ∂ xn ⋮ ⋮ ⋮ ∂ fm ( x ) ∂ x 1 ∂ fm ( x ) ∂ x 2 ⋯ ∂ fm ( x ) ∂ xn ] J(x )=\left[ \begin{matrix} \frac{
{\partial}f_1(x)}{
{\partial}x_1} & \frac{
{\partial}f_1(x)}{ {
\partial}x_2} & \cdots& \frac{
{\partial}f_1(x)}{
{\partial}x_n}\\ \frac{ {
\partial}f_2(x)}{
{\partial}x_1} & \frac{ {
\partial} f_2(x)}{
{\partial}x_2} & \cdots& \frac{
{\partial}f_2(x)}{
{\partial}x_n}\\ \vdots & \vdots & &\vdots\\ \frac{
{\partial}f_m(x)}{
{\partial}x_1} & \frac{
{\partial}f_m(x)}{
{\partial}x_2} & \cdots& \frac{
{\partial}f_m(x) }{
{\partial}x_n} \end{matrix} \right]J ( x )=
∂ x1∂f _1( x )∂ x1∂f _2( x )⋮∂ x1∂f _m( x )∂ x2∂f _1( x )∂ x2∂f _2( x )⋮∂ x2∂f _m( x )⋯⋯⋯∂ xnorte∂f _1( x )∂ xnorte∂f _2( x )⋮∂ xnorte∂f _m( x )
Es fácil ver que el gradiente ∇ f ( x ) {\nabla}f(x)La
matrizjacobiana de ∇ f (
__ ^n{\rightarrow}RF:Rn →Res continuamente diferenciable,p ∈ R np{\in}R^np∈Rn,那么
f ( x + p ) = f ( x ) + ∇ ( x + t p ) T p f(x+p)=f(x)+{\nabla}(x+tp)^Tp f(x+p)=f(x)+∇(x+tp)Tp
其中 0 < t < 1 0<t<1 0<t<1,进一步,如果说 f f f是二阶连续可微的
f ( x + p ) = f ( x ) + ∇ f ( x ) T p + 1 2 p T ∇ 2 f ( x + t p ) p f(x+p)=f(x)+{\nabla}f(x)^Tp+\frac{1}{2}p^T{\nabla}^2f(x+tp)p f(x+p)=f(x)+∇f(x)Tp+21pT∇2f(x+tp ) p
其中0 < t < 1 0<t<10<t<1
Finalmente, este capítulo también presenta un tipo especial de función diferenciable: la función continua de Lipschitz de gradiente. Este tipo de función juega un papel clave en demostrar la convergencia de muchos algoritmos de optimización. Función continua de Lipschitz de gradiente Definición: Dada una función
diferenciable fff , si existeL > 0 L>0l>0 , para cualquierx , y ∈ domfx,y{\in}domfx ,y ∈ d o m f tiene (domf domfd o m f esffdominio de f
) ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ≤ L ∣ ∣ x − y ∣ ∣ ||{\nabla}f(x)-{\nabla}f(y)|| { \le}L||xy||∣∣ ∇ f ( x )−∇f(y)∣∣≤L∣∣x−y∣∣
则称 f f f是梯度利普希茨连续的,相应利普希茨常数为 L L L,有时候也会称为 L L L-光滑,或者梯度 L L L-利普希茨连续
梯度利普希茨连续表明, ∇ f ( x ) {\nabla}f(x) ∇f(x)的变化可以被自变量 x x x的变化所控制,满足该性质的函数有很多很好的性质, 一个重要的性质就是具有二次上界
具体证明我这里我就不再过多阐述了,有二次上界就是说 f ( x ) f(x) f(x)可以被一个二次函数上界所控制,即要求说 f ( x ) f(x) f(x)的增长速度不超过二次
还有一个推论就是说,如果 f f f是梯度利普希茨连续的,且有一个全局最小点 x ∗ x^* x∗,我们可以利用二次上界来估计 f ( x ) − f ( x ∗ ) f(x)-f(x^*) f(x)−f(x∗)的大小,其中 x x x可以是定义域中任意一点
1 2 L ∣ ∣ ∇ f ( x ) ∣ ∣ 2 ≤ f ( x ) − f ( x ∗ ) \frac{1}{2L}||{\nabla}f(x)||^2{\le}f(x)-f(x^*) 2L1∣∣∇f(x)∣∣2≤f(x)−f(x∗)
具体的证明我这里就不写了哈,想知道的可以百度或者我们讨论一下
2.2.2 矩阵变量函数的导数
La definición de gradiente de función multivariada también se puede extender al caso donde la variable es una matriz, con m ∗ nm*nmetro∗n matrizXX_X es la función f (X) f(X)de la variable independientef ( X ) , si hay una matrizG ∈ R m ∗ n G{\in}R^{m*n}GRAMO ∈ Rm ∗ n满足
lim V → 0 f ( X + V ) − f ( X ) − < G , V > ∣ ∣ V ∣ ∣ = 0 \lim_{V{\rightarrow}0}\frac{f(X+ V)-f(X)-<G,V>}{||V||}=0V → 0lím∣∣ V ∣∣f ( X+V )−f ( X ) −<GRAMO ,V>=0donde∣ ∣ ⋅ ∣ ∣ ||·
||∣∣ ⋅∣∣是任意矩阵范数,就称矩阵向量函数 f f f在 X X X处 F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微,就称G为 f f f在 F r a ˊ c h e t Fr\acute{a}chet Fraˊchet可微意义下的梯度,其实矩阵变量函数 f ( X ) f(X) f ( X )的梯度也可以用其偏导数表示为
∇ f ( x ) = [ ∂ f ∂ x 11 ∂ f ∂ x 12 ⋯ ∂ f ∂ x 1 n ∂ f ∂ x 21 ∂ f ∂ x 22 ⋯ ∂ f ∂ x 2 n ⋮ ⋮ ⋮ ∂ f ∂ xm 1 ∂ f ∂ xm 2 ⋯ ∂ f ∂ xmn ] {\nabla}f(x)=\left[ \begin{matrix} \frac{ {\partial}f
} {
{\partial}x_{11}} & \frac{
{\partial}f}{
{\partial}x_{12}} & \cdots& \frac{
{\partial}f}{ {
\partial}x_{1n }}\\ \frac{
{\partial}f}{
{\partial}x_{21}} & \frac{
{\partial}f}{
{\partial}x_{22}} & \cdots& \frac{
{ \partial}f}{
{\partial}x_{2n}}\\ \vdots & \vdots & &\vdots\\ \frac{ {\
partial}f}{
{\partial}x_{m1}} & \frac{
{\partial}f}{
{\partial}x_{m2}} & \cdots& \frac{
{\partial}f}{
{\partial}x_{mn} } \end{matriz} \right]∇f ( x ) _=
∂ x11∂f _∂ x21∂f _⋮∂ xmetro 1∂f _∂ x12∂f _∂ x22∂f _⋮∂ xmetros 2∂f _⋯⋯⋯∂ x1 norte∂f _∂ x2 norte∂f _⋮∂ xmn∂f _
F ra ˊ chet Fr\acute{a}chetfr _aˊ La definición y el uso de chetdiferenciable son a menudo engorrosos, por lo que existe otra definición -----G a ^ teaaux G\hat{a}teauxGRAMOa^teaux可微
定义:设 f ( X ) f(X) f(X)为矩阵变量函数,如果存在矩阵 G ∈ R m ∗ n G{\in}R^{m*n} G∈Rm∗n对任意方向 V ∈ R m ∗ n V{\in}R^{m*n} V∈Rm∗n满足
lim t → 0 f ( X + t V ) − f ( X ) − t < G , V > t = 0 \lim_{t{\rightarrow}0}\frac{f(X+tV)-f(X)-t<G,V>}{t}=0 t→0limtf(X+tV)−f(X)−t<G,V>=0
则称 f f fAcerca de XX_X是G a ^ téaux G\hat{a}teauxGRAMOa^ teaux, llame aGfff在G a ^ teaux G\hat{a}teauxGRAMOa^ teauxgradiente en el sentido diferenciable
siF ra ˊ chet Fr\acute{a}chetfr _aˊ chetes diferenciable y podemos deducirG a ^ teaaux G\hat{a}teauxGRAMOa^ teauxes diferenciable, pero no al revés, pero las funciones analizadas en este libro son básicamenteF ra ˊ chet Fr\acute{a}chetfr _aˊ chetes diferenciable, por lo que no es necesario discutirlo por el momento. Es bueno que todos entiendan ~, función variable de matriz unificadaf (X) f(X)La derivada de f ( _
_
_∂ X∂f _O ∇ f ( X ) {\nabla}f(X)∇f ( X ) _
Por poner un ejemplo, en caso de que no sepas para qué sirve,
considera una función lineal: f (X) = T r (AXTB) f(X)=Tr(AX^TB)f ( X )=T r ( A XT B),其中A ∈ R p ∗ n , B ∈ R m ∗ p , X ∈ R m ∗ n A{\in}R^{p*n},B{\in}R^{m*p} ,X{\in}R^{m*n}Un ∈ Rp ∗ norte ,segundo ∈ rmetro ∗ pag ,X∈R _ _m ∗ n para cualquier direcciónV ∈ R m ∗ n V{\in}R^{m*n}V∈R _ _m ∗ n以及t ∈ R t{\in}Rt ∈ R,有
lim t → 0 f ( X + t V ) − f ( X ) t = lim t → 0 T r ( A ( X + t V ) TB − T r ( AXTB ) ) t \lim_ {t{\rightarrow}0}\frac{f(X+tV)-f(X)}{t}=\lim_{t{\rightarrow}0}\frac{Tr(A(X+tV)^TB -Tr(AX^TB))}{t}t → 0límtf ( X+t V )−f ( X )=t → 0límtT r ( A ( X+t V )TB _−T r ( A XT B) )
= T r ( AVTB ) = < BA , V > =Tr(AV^TB)=<BA,V>=T r ( A VTB )_=<BA , _V>
Entonces,∇ f ( X ) = BA {\nabla}f(X)=BA∇f ( X ) _=B A
Cuando supe esto, tuve una pregunta, es decir,T r (AVTB) = <BA, V> Tr(AV^TB)=<BA,V>T r ( A VTB )_=<BA , _V> ¿ Por qué?
Sabemos queT r (AVTB) = T r (BAVT) Tr(AV^TB)=Tr(BAV^T)T r ( A VTB )_=T r ( B A VT )Esta es la propiedad básica de la traza,BA BAB A sumaVVV son todosm ∗ nm*nmetro∗n的,那么这时候又有一个性质,假设C和D是相同规模的矩阵,那么 T r ( A T B ) = < A , B > Tr(A^TB)=<A,B> Tr(ATB)=<A,B>
我这里是参考知乎jordi的,这是他的一个关于3*3矩阵的推导
链接:https://www.zhihu.com/question/274052744/answer/1521521561

那么这样就可以推出 T r ( A V T B ) = T r ( V T , B A ) = < B A , V > Tr(AV^TB)=Tr(V^T,BA)=<BA,V> Tr(AVTB)=Tr(VT,BA)=<BA,V>啦
2.2.3 自动微分
自动微分是使用计算机导数的算法,在神经网络中,我们通过前向传播的方式将输入数据 a a a转化为 y ^ \hat{y} y^,也就是将输入数据 a a a作为初始信息,将其传递到隐藏层的每个神经元,处理后输出得到 y ^ \hat{y} y^。
通过比较输出得到 y ^ \hat{y} y^与真实标签y,可以定义一个损失函数 f ( x ) f(x) f(x),其中 x x x表示所有神经元对饮的参数集合, f ( x ) f(x) f(x)一般是多个函数复合的形式,为了找到最优的参数,我们需要通过优化算法来调整 x x x使得 f ( x ) f(x) f(x)达到最小,因此,对神经元参数 x x x的计算是不可避免的
这一块就是讲了一个神经网络的前向传播和后向求导,自动微分有两种方式,前向模式和后向模式,前向模式就是变传播变求导,后向模式就是前传播再一层层求导,很显然现在大家学的都是后向模式这种的吧,因为他复杂度更低,计算代价小
2.3 广义实值函数
En el curso del análisis matemático, aprendimos el concepto básico de función: una función se deriva del espacio vectorial R n R^nRn al campo de datosRREl mapeo de R , en el campo de la optimización, a menudo implica realizar una operación inf(sup) en una variable de una función, lo que da como resultado que el valor de la función posiblemente sea infinito. Para describir el problema de optimización de manera más conveniente, necesitamos La definición de la función se amplía de alguna manera.
Entonces, ¿qué es una función de valor real generalizada?
SeaR ˉ = R ⋃ ∞ \bar{R}=R{\bigcup}{\infty}Rˉ=R ⋃ ∞ es un espacio de números reales generalizado, entonces el mapeof : R n → R ˉ f:R^n{\rightarrow}\bar{R}F:Rnorte →Rˉ se llama función generalizada de valor real. Puede ver que hay dos valores especiales más en el rango de valores, más y menos infinito.
2.3.1 Funciones apropiadas
Función adecuada: Dada una función de valor real generalizada fff y el conjunto no vacíoXXX , si existex ∈x ∈ X tal quef ( x ) < + ∞ f(x)<+{\infty}f ( x )<+ ∞ , y para cualquierx ∈x ∈ X , todos tienenf ( x ) > − ∞ f(x)>-{\infty}f ( x )>− ∞ , entonces llamamos a la funciónfffAcerca de la colecciónXXX es apropiado.
En resumen, significa que la función apropiadaffEn cuanto a f , al menos un valor no es infinito positivo y el valor en todas partes no es infinito negativo. Para problemas de optimización, las funciones apropiadas pueden ayudarnos a eliminar algunas funciones poco interesantes y considerar el problema desde una clase de función más razonable. Esto debería ser fácil de entender. Analicemos un problema mínimo. Al menos uno de sus valores no puede ser infinito positivo. De lo contrario, cómo obtener mínimo, y luego los valores en todas partes no pueden ser infinito negativo. De lo contrario, ¿cuál es el punto? de discutirlo, ¿no?
Estamos de acuerdo en que,a menos que se especifique lo contrario en este libro, las funciones analizadas en el teorema son todas funciones apropiadas.
Para la función apropiadafff , especificando su dominio
domf = { x ∣ f ( x ) < + ∞ } domf=\{x|f(x)<+{\infty}\}d o m f={
x ∣ f ( x )<+ ∞ }
Porque ciertamente es imposible obtener el valor mínimo de una función apropiada en el infinito positivo ^^
2.3.2 Función cerrada
Las funciones cerradas son otro tipo importante de funciones generalizadas de valor real. Las funciones cerradas pueden verse como una generalización de funciones continuas.
Antes de hablar de funciones cerradas, primero presentamos algunos conceptos básicos:
1. Conjunto de nivel inferior
El conjunto de nivel inferior es un concepto importante para describir el valor de una función de valor real: para este propósito, existe la siguiente definición
( α \alphaα - conjunto de nivel inferior) para funciones generalizadas de valores reales:f : R n → R ˉ f:R^n{\rightarrow}\bar{R}F:Rnorte →Rˉ
C α = { x ∣ f ( x ) ≤ α } C_{\alpha}=\{x|f(x)\le{\alpha}\}Ca={
x ∣ f ( x )≤α }
se llamaffα \alfade fα - nivel inferior establecido
significa que el valor no puede excederα \alphaα Bueno, siC α C_{\alpha}CaNo vacío, sabemos que f ( x ) f(x)f(x)的全局最小点一定落在 C α C_{\alpha} Cα中,无需考虑之外的点
2.上方图
上方图是从集合的角度来描述一个函数的具体性质,有如下定义:
对于广义实值函数 f : R n → R ˉ f:R^n{\rightarrow}\bar{R} f:Rn→Rˉ
e p i f = { ( x , t ) ∈ R n + 1 ∣ f ( x ) ≤ t } epif=\{(x,t){\in}R^{n+1}|f(x){\le}t\} epif={(x,t)∈Rn+1∣f(x)≤t}
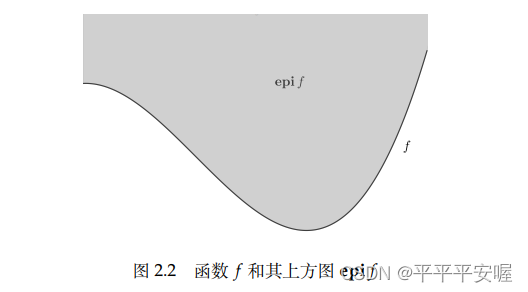
说人话就是函数 f f f上方的东西小于等于t(t取任意值), f f f的很多性质都可以通过 e p i f epif e p i f se puede obtener a través deepif epifAlgunas propiedades de e p i f ffpropiedades de f
3. Funciones cerradas y funciones semicontinuas inferiores.
Función cerrada: Sea f : R n → R ˉ f:R^n{\rightarrow}\bar{R}F:Rnorte →Rˉ es una función de valor real generalizada, siepif epife p si f es un conjunto cerrado, entonces se llamafff es una función cerrada.
La función semicontinua inferior: Sea la función de valor real generalizadaf : R n → R ˉ f:R^n{\rightarrow}\bar{R}F:Rnorte →Rˉ , si para cualquierx ∈ R nx{\in}R^nx∈R _ _n,有
lim inf y → xf ( y ) ≥ f ( x ) \liminf_{y{\rightarrow}x} f(y)\ge{f(x)}y → xLiminff ( y )≥f ( x )
entoncesf ( x ) f(x)f ( x ) es una función semicontinua inferior
Creo que si no comprende este límite inferior, sería mucho mejor leer el texto directamente.
De hecho, está en x 0 x_0X0En la vecindad de , si f( x 0 x_0X0) menos un valor pequeño positivo, de modo que siempre sea menor que todos los f ( x ) f(x) en la vecindadf ( x ) , se dice que hay una semicontinuidad inferior en el punto de discontinuidad.
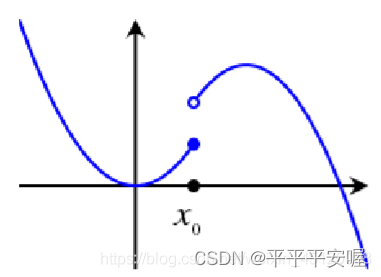
Si se parece a la imagen de abajo,
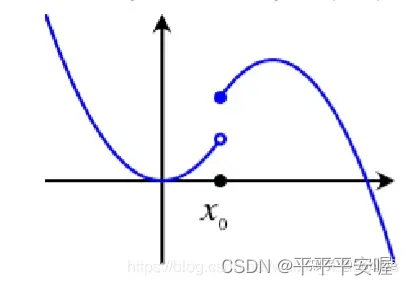
tux 0 x_0X0Si avanzas aunque sea un poquito más hacia la izquierda, caerá bruscamente y no llegarás a x 0 x_0X0xx en el barrio dex比f ( x 0 ) − ε f(x_0)-{\varepsilon}f ( x0)−ε es grande, y si es la primera imagen, podemos garantizarx 0 x_0X0El lado izquierdo de no caerá bruscamente , eso es más o menos lo que significa
Sea la función generalizada de valor real f : R n → R ˉ f:R^n{\rightarrow}\bar{R}F:Rnorte →Rˉ . Entonces las siguientes proposiciones son equivalentes:
(1)f ( x ) f(x)Cualquierα \alpha de f ( x )Los conjuntos de nivel inferior α son todos conjuntos cerrados
(2)f ( x ) f(x)f ( x ) es semicontinuo inferior
(3)f ( x ) f(x)F ( _ _ _
_
_ , entonces el conjunto es cerrado.
Podemos ver que, de hecho, las funciones cerradas y las funciones semicontinuas inferiores pueden ser equivalentes. En el futuro, a menudo solo aparecerá una definición.
Operaciones simples entre cerradas (inferiores semicontinuas) las funciones mantendrán las propiedades originales
(1) suma, sifff yggg son funciones cerradas apropiadas, ydomf ⋂ domg ≠ ∅ domf {\bigcap}domg{\neq}∅d o m f ⋂ d o m g= ∅entoncesf + g f+gF+g también es una función cerrada, es apropiado evitar la situación de fórmula indeterminada, es decir,
la combinación de infinito negativo + infinito positivo (2) mapeo afín, sifff es una función cerrada, entoncesf (A x + b) f(Ax+b)f ( Un x+b ) también toma la cota suprema para la función cerrada
(3), si toda funciónf α f_{\alpha}Fason todas funciones cerradas, entonces sup α f α ( x ) sup_{\alpha}f_{\alpha}(x)sup _ _aFa( x ) también es una función cerrada.
2.4 colección convexa
2.4.1 Definiciones relacionadas de conjuntos convexos
Para ser honesto, siempre había oído hablar de conjuntos convexos antes, pero nunca entendí la definición específica. Aprendamos sobre esto ahora ~
Para R n R^nRDos puntos en n x 1 ≠ x 2 x_1{\neq}x2X1= x2,形如
y = θ x 1 + ( 1 − θ ) x 2 y={\theta}x_1+(1-{\theta})x_2y=θ x1+( 1−yo ) x2
Los puntos forman el punto de paso x 1 x_1X1y x 2 x_2X2línea recta, cuando 0 ≤ θ ≤ 1 0{\le}{\theta}{\le}10 ≤ θ ≤ 1 , dichos puntos forman el punto de conexiónx 1 x_1X1con x 2 x_2X2
Definimos el segmento de recta : si pasa por el conjunto CCLa rectaentre dos puntos cualesquiera de C se encuentra enCC.Dentro de C , se llamaCC.C esun conjunto afín, es decir,
x 1 , x 2 ∈ C ⟶ θ x 1 + ( 1 − θ ) x 2 ∈ C , ∀ θ ∈ R x_1,x_2{\in}C{\longrightarrow}{\theta }x_1+ (1-{\theta})x_2{\in}C,{\forall}{\theta}{\in}RX1,X2∈ C ⟶ θx _1+( 1−yo ) x2∈ C , ∀ θ ∈ R
Es obvio que el sistema de ecuaciones linealesA x = b Ax=buna x=El conjunto solución de b es un conjunto afín, por el contrario, cualquier conjunto afín puede expresarse como un conjunto solución de un sistema de ecuaciones lineales.
Entonces, ¿cuál es la definición de conjunto convexo?
Conjunto convexo: Si conecta el conjunto CCLos segmentos de rectade dos puntos cualesquiera en C están enCCDentro de C , se llamaCC.C为凸集,即
x 1 , x 2 ∈ C ⟶ θ x 1 + ( 1 − θ ) x 2 ∈ C , ∀ 0 ≤ θ ≤ 1 x_1,x_2{\in}C{\longrightarrow}{\theta} x_1+(1-{\theta})x_2{\in}C,{\forall}0{\le}{\theta}{\le}1X1,X2∈ C ⟶ θx _1+( 1−yo ) x2C _ _ _ _ _ _ _ _
_
_
_ = θ 1 x 1 + θ 2 x 2 + ⋯ + θ kxkx={\theta}_1x_1+{\theta}_2x_2+\cdots+{\theta}_kx_kX=i1X1+i2X2+⋯+ikXk
1 = θ 1 + θ 2 + ⋯ + θ k , θ i ≥ 0 , i = 1 , 2 , ⋯ , k 1={\theta}_1+{\theta}_2+\cdots+{\theta}_k,{\theta }_i{\ge}0,i=1,2,\cdots,k1=i1+i2+⋯+ik, yoyo≥ 0 ,i=1 ,2 ,⋯,
Los puntos de k se llaman x 1 , x 2 , ⋯ , xk x_1,x_2,\cdots,x_kX1,X2,⋯,XkCombinación convexa de , conjunto SSEl conjunto de todas las combinaciones convexas de puntos medios en S se llama SS.El casco convexo de S se denota comoconv S conv Sconv S , en resumen,conv S convScon v S contieneSS _El conjunto convexo más pequeño de S
Si θ i ≥ 0 {\theta}_i{\ge}0 se elimina de la definición de combinación convexaiyoRestricción ≥ 0 , podemos obtener el concepto de paquete afín
Paquete afín: LetSSS esRnR^nREl subconjunto de n
se llama el siguiente conjunto como bolsa afín de S: { x ∣ x = x = θ 1 x 1 + θ 2 x 2 + ⋯ + θ kxk , x 1 , x 2 , ⋯ , xk ∈ S , θ 1 + θ 2 + ⋯ + θ k = 1 } \{x|x=x={\theta}_1x_1+{\theta}_2x_2+\cdots+{\theta}_kx_k, x_1,x_2,\cdots,x_k{\in } S,{\theta} _1+{\theta}_2+\cdots+{\theta}_k=1\}{
x ∣ x=X=i1X1+i2X2+⋯+ikXk,X1,X2,⋯,Xk∈ S ,i1+i2+⋯+ik=1 }
denotado comoafín S afínSa ff in e S
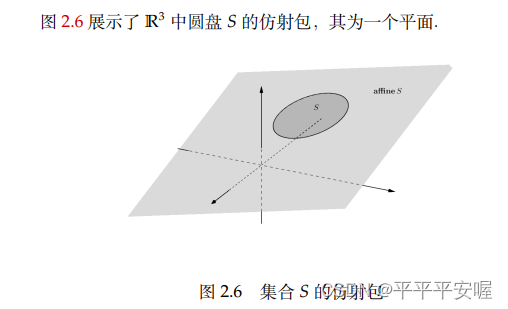 fangshebao
fangshebao
En términos generales, el paquete afín de un conjunto es en realidad el conjunto afín más pequeño que contiene el conjunto,
como
x = θ 1 x 1 + θ 2 x 2, θ 1 > 0, θ 2 > 0 x= {\theta}_1x_1+{\theta}_2x_2,{\theta}_1>0,{\theta}_2>0X=i1X1+i2X2,i1>0 ,i2>El punto de 0
se llama puntox 1 , x 2 x_1,x_2X1,X2combinación de cono, si el conjunto SSLa combinación de conos de cualquier punto en S está en SSen S , entonces S se llama cono convexo
2.4.2 Conjuntos convexos importantes
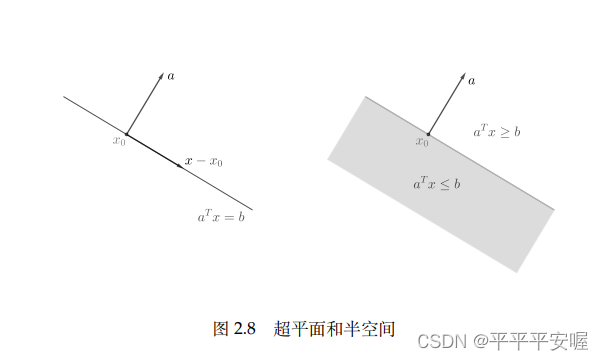
1. Hiperplano y medio espacio.
Tome cualquier vector aa distinto de ceroa,形如{ x ∣ a T x = b } \{x|a^Tx=b\}{
x ∣ aT x=El conjunto de b } se llama hiperplano, que tiene la forma{ x ∣ a T x ≤ b } \{x|a^Tx{\le}b\}{
x ∣ aEl conjunto de T x≤b}se llama medio espacio,aaa es el vector normal del correspondiente hiperplano y medio espacio. Un hiperplano seráR n R^nRn se divide en dos semiespacios. Es fácil ver que el hiperplano es un conjunto afín y un conjunto convexo, y el semiespacio es un conjunto convexo pero no un conjunto afín (esto debería ser fácil de entender si entiendes los conceptos de conjuntos afines y conjuntos convexos)
2. Esfera, elipsoide, cono
La esfera y el elipsoide también son conjuntos convexos comunes. No introduciremos la esfera aquí. La
forma es
{ x ∣ ( x − xc ) TP − 1 ( x − x ) c ) ≤ 1 } \{x|(x-x_c) ^TP^{-1}(xx)_c){\le}1\}{
x ∣ ( x−Xc)TP _− 1 (x−x )c) ≤ 1 }
se llama elipsoide, donde P es simétrico y definido positivo. Otra expresión del elipsoide es{ xc + A u ∣ ∣ u 2 ∣ ∣ ≤ 1 } \{x_c+Au||u_2||{\ le }1\}{
xc+A tu ∣∣ tu2∣∣ ≤ 1 } , A es una matriz cuadrada no singular
Además, llamamos al conjunto
{ ( x , t ) ∣ ∣ ∣ x ∣ ∣ ≤ t } \{(x,t)|||x|| {\le}t\}{( x ,t)∣∣∣x∣∣≤t}
为范数锥,欧几里得范数锥也称为二次锥,范数锥是凸集
别忘了 t t t也是变量噢,看这个图应该就很好理解范数锥了

知乎链接:https://zhuanlan.zhihu.com/p/126072881
3.多面体
我们把满足线性等式和不等式组的点的集合称为多面体,即
{ x ∣ A x ≤ b , C x = d } \{x|Ax{\le}b,Cx=d\} {
x∣Ax≤b,Cx=d}
多面体是有限个半空间和超平面的交集,所以是凸集
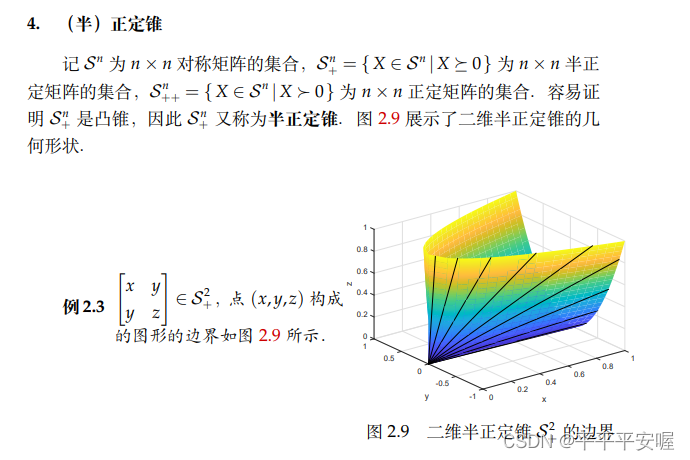
4.(半)正定锥
这个我直接把书上的先贴过来把,我目前也不太懂,就不能细说
2.4.3 保凸的运算
证明一个集合是凸集有两种方式,第一种就是利用定义
x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 ⟶ θ x 1 + ( 1 − θ x 2 ) ∈ C x_1,x_2{\in}C,0{\le}{\theta}{\le}1{\longrightarrow}{\theta}x_1+(1-{\theta}x_2){\in}C x1,x2∈ C ,0 ≤ θ ≤ 1 ⟶ θx _1+( 1−θ x2) ∈ C para demostrar el conjuntoCCC es un conjunto convexo.
El segundo método consiste en explicar que el conjunto C se puede obtener a partir de un conjunto convexo simple (el hiperplano, el medio espacio, la esfera normal, etc. que acabamos de mencionar) mediante operaciones de preservación de la convexidad.
Teorema 1: La intersección de múltiples conjuntos convexos es un conjunto convexo
Teorema 2: Seaf : R n → R mf:R^n{\rightarrow}R^mF:Rnorte →Rm是仿射变换(f ( x ) = A x + b , A ∈ R m ∗ n , b ∈ R nf(x)=Ax+b,A{\in}R^{m*n},b{ \en}R^nf ( x )=una x+segundo ,Un ∈ Rmetro ∗ norte ,segundo ∈ Rn ), entonces
(1) el conjunto convexo está enffLa imagen bajo f
es un conjunto convexo: S es un conjunto convexo → f ( S ) → { f ( x ) ∣ x ∈ S } es un conjunto convexo S es un conjunto convexo {\rightarrow}f(S){\rightarrow }\{f (x)|x{\in}S\} es un conjunto convexoS es un conjunto convexo → f ( S ) → {
f ( x ) ∣ x ∈ S } es un conjunto convexo
(2) El conjunto convexo está enffLa imagen original bajo f
es un conjunto convexo C es un conjunto convexo → f − 1 ( C ) → { x ∈ R n ∣ f ( x ) ∈ C } es un conjunto convexo C es un conjunto convexo {\rightarrow}f^ {-1} (C){\rightarrow}\{x{\in}R^n|f(x){\in}C\} es un conjunto convexoC es un conjunto convexo → f− 1 (C)→{
x∈Rn ∣f(x)∈C}es un conjunto convexo
, es decir, sigue siendo un conjunto convexo después de escalado, traslación o proyección.
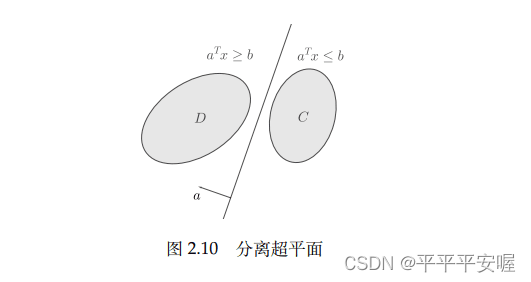
2.4.4 Teorema del hiperplano de separación
Esta es una propiedad importante de los conjuntos convexos, es decir, los conjuntos convexos disjuntos pueden separarse mediante hiperplanos. Los resultados más básicos son el teorema del hiperplano de separación y el teorema del hiperplano de apoyo. El teorema del hiperplano de separación: si C y D son dos conjuntos convexos
disjuntos , entonces hay un vector distinto de cero aaa y changshubbb,使得
a T x ≤ b , ∀ x ∈ C , 且 a T x ≥ b , ∀ x ∈ D a^Tx{\le}b,{\forall}x{\in}C,且a^Tx{ \ge}b,{\forall}x{\in}DaT x≤b,∀ x ∈ C ,y unT x≥b,∀ x ∈ D
es el hiperplano{ x ∣ a T x = b } \{x|a^Tx=b\}{
x ∣ aT x=b } CCseparadosC yDDD
teorema de separación estricta: es decir, el signo de desigualdad estricta se establece arriba. No ampliaré los detalles.
Hiperplano de soporte: conjunto dadoCCUn punto x 0 x_0en C y su fronteraX0, si a ≠ 0 a{\neq}0a= 0满足a T x ≤ a T x 0 , ∀ x ∈ C a^Tx{\le}a^Tx_0,{\forall}x{\in}CaT x≤aT x0,∀ x ∈ C , entonces el conjunto
{ x ∣ a T x = a T x 0 } \{x|a^Tx=a^T{x_0}\}{
x ∣ aT x=aT x0}
paraCCC está en el punto límitex 0 x_0X0El hiperplano de soporte
en es geométricamente hablando, este hiperplano es idéntico al conjunto CCC está en el puntox 0 x_0X0tangente al
teorema del hiperplano de soporte: si C es un conjunto convexo, entonces hay un hiperplano de soporte en cualquier punto límite de C.
Este teorema en realidad tiene una intuición geométrica muy fuerte, es decir, después de que se da un plano, el límite del conjunto convexo puede ser Cualquier punto del conjunto convexo se utiliza como punto de apoyo para colocar el conjunto convexo en el plano, y los conjuntos de otras formas generalmente no tienen esta propiedad.
2.5 funciones convexas
Todo el mundo debe haber oído hablar de la función convexa, echemos un vistazo a su definición específica (todavía no sé mucho al respecto)
2.5.1 Definición de función convexa
Función convexa: deja que la función fff es una función apropiada sidomf domfd o m f en el campo, de
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f({\theta}x+(1-{\theta })y){\le}{\theta}f(x)+(1-{\theta})f(y)f ( θx _+( 1−θ ) y ) ≤ θ f ( x )+( 1−θ ) f ( y )
Para todox , y ∈ domf , 0 ≤ θ ≤ 1 x,y{\in}domf,0{\le}{\theta}{\le}1x ,y ∈ re o m f ,0 ≤ θ ≤ 1 es verdadero y se llamafff es una función convexa.
Intuitivamente hablando, el segmento de línea que conecta dos puntos cualesquiera en la imagen de la función convexa está por encima de la imagen de la función.
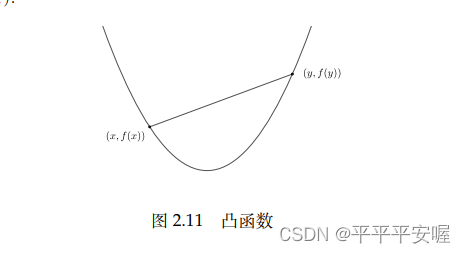
En consecuencia, también tenemos una función cóncava, si− f -f− f es una función convexa, entonces se llamafff es una función convexa. Muchas propiedades de las funciones convexas se pueden aplicar a funciones cóncavas simplemente cambiando el signo.
Además, sidomf domfd o m f rango, desde
f ( θ x + ( 1 − θ ) y ) < θ f ( x ) + ( 1 − θ ) f ( y ) f({\theta}x+(1-{\theta }) y)<{\theta}f(x)+(1-{\theta})f(y)f ( θx _+( 1−i ) y )<θ f ( x )+( 1−θ ) f ( y )
y seax , y ∈ domf , x ≠ y , 0 ≤ θ ≤ 1 x,y{\in}domf,x{\neq}y,0{\le}{\theta}{ \ y 1x ,y ∈ re o m f ,X= y,0 ≤ θ ≤ 1 es cierto, entonces se llamafff es una función estrictamente convexa.
Hay otro tipo de función convexa de uso común,la función fuertemente convexa
. Función convexa fuerte, si hay una constantem > 0 m>0metro>0 , haciendo
g ( x ) = f ( x ) − m 2 ∣ ∣ x ∣ ∣ 2 g(x)=f(x)-\frac{m}{2}||x||^2g ( x )=f ( x )−2m∣∣ x ∣ ∣2
es una función convexa, entonces se llamaf ( x ) f(x)f ( x ) es una función fuertemente convexa, dondemmm esuna función fuertemente convexa, que también se puede llamar función m-fuertemente convexa.
Seag (x) g(x)Aplicando g ( x ) a la definición de función convexa, podemos obtener
Si hay una constantem > 0 m>0metro>0 , tal que para cualquierx, y ∈ domf, 0 < θ < 1 x,y{\in}domf, 0<{\theta}<1x ,y ∈ re o m f ,0<i<1 , si
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) − m 2 θ ( 1 − θ ) ∣ ∣ x − y ∣ ∣ 2 f( {\theta}x+(1-{\theta})y){\le}{\theta}f(x)+(1-{\theta})f(y)-\frac{m}{2}{ \theta}(1-{\theta})||xy||^2f ( θx _+( 1−θ ) y ) ≤ θ f ( x )+( 1−yo ) f ( y )−2myo ( 1−yo ) ∣∣ x−y ∣ ∣2
se llamaf ( x ) f(x)f ( x ) es una función fuertemente convexa, dondemmm es un parámetro fuertemente convexo.
De estas dos definiciones, podemos ver que:
(1) Una función fuertemente convexa menos una función cuadrática definida positiva sigue siendo convexa
(2) Una función fuertemente convexa debe ser una función estrictamente convexa,m = 0 metro=0metro=Degenera en una función convexa en 0.

Un teorema importante: Seafff es una función fuertemente convexa y tiene un valor mínimo, entonces su punto de valor mínimo es único. La
prueba específica se puede probar por contradicción. Es bastante simple. Supongamos que hay dos puntos de valor mínimox, yx, yx ,y , y luego sustitúyalo en la definición de función fuertemente convexa
. Cabe señalar queffLa existencia de un valor mínimo de f es una premisa; de lo contrario, es posible que no exista necesariamente el punto mínimo global de una función fuertemente convexa.
2.5.2 Teorema de determinación de la función convexa
Uno de los métodos más básicos para determinar una función convexa es limitarla primero a cualquier línea recta y luego determinar si la función unidimensional correspondiente es convexa.
Teorema 1: f (x) f(x)f ( x ) es una función convexa si y solo si para cualquierx ∈ domf , v ∈ R n , g : R → R x{\in}domf,v{\in}R^n,g:R{\rightarrow }Rx ∈ re o m f ,v ∈ Rnorte ,gramo:R → R,
g ( t ) = f ( x + tv ) , domg = { t ∣ x + tv ∈ domf } g(t)=f(x+tv), domg=\{t|x+tv{\ en}domf\}g ( t )=f ( x+televisión ) , _domg={
t∣x+tv∈domf}
是凸函数
具体证明说难也不难说简单也不简单,想弄明白的百度或者来和我探讨一下哈(我是看了大概二十分钟半小时才看懂TT)
这里先给出一些实际中经常遇到的一些凸(凹)函数吧
(1)指数函数: e a x , a , x ∈ R e^{ax},a,x{\in}R eax,a,x∈R是凸函数
(2)幂函数: x a ( x > 0 ) x^a(x>0) xa(x>0),当 α ≥ 1 \alpha{\ge}1 α≥1或 α ≤ 0 {\alpha}{\le}0 Cuando α ≤ 0 , es una función convexa
(3) entropía negativa:xlnx ( x > 0 ) xlnx(x>0)x l norte x ( x>0 ) es una función convexa
(4) Todas las normas son funciones convexas (versiones vectoriales y matriciales)ff
definida en un conjunto convexof,fff es una función convexa si y sólo si
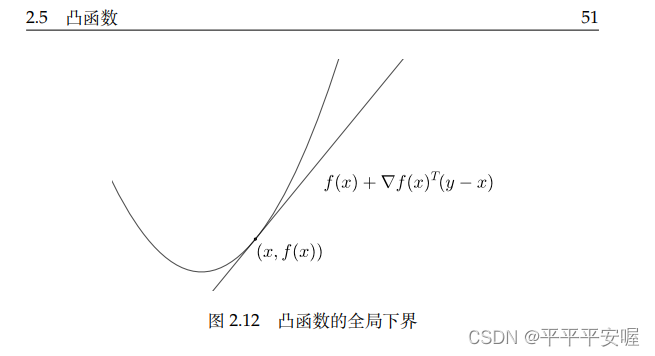
f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) , ∀ x , y ∈ domff(y){\ge}f(x)+{ \ nabla}f(x)^T(yx),{\forall}x,y{\in}dom ff ( y ) ≥ f ( x )+∇f ( x ) _T (y−x ) ,∀ x ,
La prueba específica de y ∈ do m f es la misma que la anterior. Esta prueba es relativamente simple. Este
teorema muestra que la función convexa diferenciableffLa gráfica de f siempre está por encima de la tangente de cualquier punto, por lo tanto, con la función convexa diferenciableffLa aproximación de primer orden de f en cualquier punto se puede obtener comoffUn límite inferior global de f
Teorema 3: Monotonicidad del gradiente, seaff es una función derivable, entoncesfff es una función convexa si y sólo sidomf domfd o m f es convexo y∇ f {\nabla}f∇ f es un mapeo monótono, es decir:
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 0 , ∀ x , y ∈ domf ({\nabla}f(x)-{\ nabla} f(y))^T(xy){\ge}0,{\forall}x,y{\in}domf( ∇f ( x ) _−∇f ( y ) ) _T (x−y ) ≥ 0 ,∀ x ,y ∈ d o m f
No se mencionará la prueba específica
Inferencia: Seafff es una función diferenciable ydomf domfd o m f es un conjunto convexo, entonces
(1)fff es estrictamente convexa si y sólo si
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) > 0 , ∀ x , y ∈ domf ({\nabla}f(x)-{\nabla } f(y))^T(xy)>0,{\forall}x,y{\in}domf( ∇f ( x ) _−∇f ( y ) ) _T (x−y )>0 ,∀ x ,y ∈ re o m f
(2)fff es una función m-fuertemente convexa si y sólo si
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ m ∣ ∣ x − y ∣ ∣ 2 , ∀ x , y ∈ domf ({ \ nabla}f(x)-{\nabla}f(y))^T(xy){\ge}m||xy||^2,{\forall}x,y{\in}domf( ∇f ( x ) _−∇f ( y ) ) _T (x−y ) ≥ metro ∣∣ x−y ∣ ∣2 ,∀ x ,y ∈ re o m f
Además, si la función es continuamente diferenciable de segundo orden, podemos obtener el siguiente
teorema de la condición de segundo orden:
Sea fff es una función diferenciable continua de segundo orden definida en un conjunto convexo, entoncesfff es una función convexa si y sólo si
∇ 2 f ( x ) ≥ 0 , ∀ x ∈ domf {\nabla^2f(x){\ge}0},{\forall}x{\in}domf∇2 f(x)≥0,∀ x ∈ do m f
si∇ 2 f ( x ) > 0 , ∀ x ∈ domf {\nabla}^2f(x)>0,{\forall}x{\in} domf∇2f (x)_>0 ,∀ x ∈ d o m f , entoncesfh fhf h es una función estrictamente convexa.
Este número también se aprende y es bastante fácil de usar. Cuando la función es continua de segundo orden y diferenciable, suele ser más conveniente usar este
2.5.3 Operaciones de conservación de la convexidad
Primero resumamos los tres métodos utilizados para demostrar que una función es convexa:
(1) Uno es usar la definición para verificar la convexidad, generalmente limitando la función a una línea recta
(2) El otro es usar condiciones de primer orden y condiciones de segundo orden para probar la función La convexidad de
(3) La tercera es estudiar directamente ffLa imagen superior de f epif epif.e p si
ahora ff _f se puede obtener a partir de una función convexa simple mediante algunas operaciones que preservan la convexidad.Teorema
:
(1) Sifff es una función convexa, entoncesα f {\alpha}fα f es una función convexa, dondeα ≥ 0 {\alpha}{\ge}0α ≥ 0
(2) Sif 1 , f 2 f_1,f_2F1,F2es una función convexa, entonces f 1 + f 2 f_1+f_2F1+F2es una función convexa
(3) si fff es una función convexa, entoncesf ( A x + b ) f(Ax+b)f ( Un x+b ) es una función convexa
(4) sif 1 , f 2 , . . . , fm f_1,f_2,...,f_mF1,F2,... ,Fmes una función convexa, entonces f ( x ) = max { f 1 ( x ) , f 2 ( x ) , . . . , fm ( x ) } f(x)=max\{f_1(x),f_2(x ) ,...,f_m(x)\}f ( x )=ma x {
f1( x ) ,F2( x ) ,... ,Fm( x )} es una función convexa
(5) si para caday ∈ A , f ( x , y ) y{\in}A,f(x,y)y ∈ A ,f ( x ,y ) Acerca dexxx es una función convexa, entonces
g ( x ) = supy ∈ A f ( x , y ) g(x)={sup}_{y{\in}A}f(x,y)g ( x )=sup _ _y ∈ Af ( x ,y )
es una función convexa
(6) Función dadag : R n → R , h : R → R g:R^n{\rightarrow}R,h:R{\rightarrow}Rgramo:Rnorte →R,h:R → R,令f ( x ) = h ( g ( x ) ) f(x)=h(g(x))f ( x )=h ( g ( x )) siggg es una función convexa,hhh es una función convexa y monótonamente no decreciente, entoncesfff es una función convexa, siggg es una función cóncava,hhh es una función convexa y no aumenta monótonamente, entoncesfff es una función convexa
(7) Función dadag : R n → R k , h : R k → R g:R^n{\rightarrow}R^k,h:R^k{\rightarrow}Rgramo:Rnorte →Rk ,h:Rk →R,
f ( x ) = h ( g ( x ) ) = h ( g 1 ( x ) , g 2 ( x ) , . . . , gk ( x ) ) f(x)=h(g(x ))=h(g_1(x),g_2(x),...,g_k(x))f ( x )=h ( g ( x ))=h ( gramo1( x ) ,gramo2( x ) ,... ,gramok( x
) ) gi g_igramoyoes una función convexa, hhh es una función convexa y monótonamente no decreciente con respecto a cada componente, entoncesfff es una función convexa, sigi g_igramoyoes una función cóncava, hhh es una función convexa y no aumenta monótonamente, entoncesfff es una función convexa
(8) sif ( x , y ) f(x,y)f ( x ,y )关于( x , y ) (x,y)( x ,y ) es una función convexa en general,CCC es un conjunto convexo, entonces
g ( x ) = infy ∈ C f ( x , y ) g(x)=inf_{y{\in}C}f(x,y)g ( x )=en fy ∈ Cf ( x ,y )
es una función convexa
(9) Defina la funciónf : R n → R f:R^n{\rightarrow}RF:RFunción de perspectiva g de n →R: R n ∗ R → R g:R^n*R{\rightarrow}Rgramo:Rnorte∗R → R
g ( x , t ) = tf ( xt ) , domg = { ( x , t ) ∣ xt ∈ domf , t > 0 } g(x,t)=tf(\frac{x}{t}) ,domg=\{
{(x,t)}|\frac{x}{t}{\in}domf,t>0\}gramo ( x ,t )=t f (tx) ,d o mg _={
( x ,t ) ∣tx∈ re o metro f ,t>0 }
Si f es una función convexa, entonces g es una función convexa
2.5.4 Propiedades de funciones convexas
1. Continuidad
首先先说明,前面的任何定理或者证明都没有说明凸函数是连续函数,但下面这个定理说明凸函数在定义域中内点是连续的
定理:设 f : R n → ( − ∞ , + ∞ ) f:R^n{\rightarrow}(-{\infty},+{\infty}) f:Rn→(−∞,+∞)为凸函数,对任一点 x 0 ∈ i n t d o m f x_0{\in}intdomf x0∈intdomf,有 f f f在 x 0 x_0 x0处连续,这里 i n t d o m f intdomf intdomf表示定义域 d o m f domf domf的内点
内点定义:这个点存在一个领域全含于定义域

推论:设 f ( x ) f(x) f ( x ) es una función convexa ydomf domfd o m f es un conjunto abierto, entoncesf ( x ) f(x)f ( x ) endomf domfd o m f es continuo.
La razón es muy simple: los puntos del conjunto abierto son todos puntos interiores.
2. Conjunto de nivel inferior convexo
Todos los conjuntos de nivel inferior de una función convexa son conjuntos convexos, es decir, se obtienen los siguientes resultados:
Sea f ( x ) f(x)f ( x ) es una función convexa, entoncesf (x) f(x)f ( x ) para todosα {\alpha}α -conjunto de nivel inferiorC α C_{\alpha}Caes un conjunto convexo,
para revisar el contenido anterior, probémoslo:
sea x 1 . x 2 ∈ C α x_1.x_2{\in}C_{\alpha}X1. X2∈C _a, para cualquier θ ∈ ( 0 , 1 ) {\theta}{\in}(0,1)θ ∈ ( 0 ,1 ) , primero segúnf (x) f(x)f ( x ) invariancia de
f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) ≤ θ α + ( 1 − θ ) α = α f({\theta}x_1+(1-{\theta})x_2){\and}{\theta}f(x_1)+(1-{\theta})f(x_2){\and}{ \theta} {\alpha}+(1-{\theta}){\alpha}={\alpha}f ( θx _1+( 1−yo ) x2) ≤ θ f ( x1)+( 1−yo ) f ( x2) ≤ θ α+( 1−yo ) un=αDe esta
manera podrás completar la certificación, si aún no entiendes, puedes regresar y echar un vistazo.
3. Límite inferior cuadrático
La función fuertemente convexa tiene la propiedad de límite inferior cuadrático
(límite inferior cuadrático). Sea f ( x ) f(x)f ( x ) es el parámetrommSi m es una función diferenciable fuertemente convexa, se cumple la siguiente desigualdad:
f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) + m 2 ∣ ∣ y − x ∣ ∣ 2 , ∀ x , y ∈ domff(y){\ge}f(x)+{\nabla}f(x)^T(yx)+{\frac{m}{2}}||yx||^2,{\forall } x,y{\in}domff ( y ) ≥ f ( x )+∇f ( x ) _T (y−x )+2m∣∣y _−x ∣ ∣2,∀x,La prueba de y ∈ d o m f
no se da aquí. Usando el límite inferior cuadrático, es fácil deducir que los conjuntos de nivel inferior de funciones diferenciables fuertemente convexas están todos acotados.
Corolario: Seafff es una función diferenciable fuertemente convexa, entoncesffTodoα {\alpha} de fα -el conjunto de niveles inferiores está limitado
2.6 Función conjugada
2.6.1 Definición y ejemplos de funciones conjugadas
La función conjugada es un concepto importante en el análisis convexo.
Definición de función conjugada: cualquier función apropiada ffLa función conjugada de f
se define como f ∗ ( y ) ≤ sup { y T x − f ( x ) } , x ∈ domff^*(y){\le}sup\{y^Tx-f(x)\ } ,x{\in}domfF∗(y)≤sup{
yT x−f ( x )} ,x ∈ d o m f
es simplemente una función linealy T xy^TxyLa diferencia máxima entre T x
Para cada y, deberíamos poder entenderla fácilmente mirando la imagen.
deja fff esRRFunción apropiada en R , para cualquier función ffSe pueden definir funciones conjugadas para f , y la función conjugada f ∗ f^*F∗ es siempre una función convexa.
Tomemos prestada la explicación del papel de las funciones conjugadas de Zhihu.

Para funciones conjugadas, tenemos las siguientes desigualdades importantes:
Desigualdad de Fenchel
f ( x ) + f ∗ ( y ) ≥ x T yf(x) +f ^*(y){\ge}x^Tyf ( x )+F∗ (y)≥xT y
A continuación damos las funciones conjugadas de algunas funciones comunes.
1. Función cuadrática
Considere la función cuadrática
f ( x ) = 1 2 x TA x + b T x + cf(x)=\frac{1}{2}x^TAx+b^Tx+cf ( x )=21Ximpuestos __+bT x+c
(1) convexidad fuerte (A > 0 A>0A>0):
f ∗ ( y ) = 1 2 ( y − b ) TA − 1 ( y − b ) − cf^*(y)=\frac{1}{2}(yb)^TA^{-1} (yb)-cF∗ (y)=21( y−segundo )TA _− 1 (y−segundo )−c
(2) Caso convexo general (A ≥ 0 A{\ge}0A ≥ 0 ):
f ∗ ( y ) = 1 2 ( y − b ) TA + ( y − b ) − c , domf ∗ = R ( A ) + bf^*(y)=\frac{1}{2 }(yb)^TA^+(yb)-c,domf^*=R(A)+bF∗ (y)=21( y−segundo )TA _+ (y−segundo )−c ,d o m f∗=R ( A )+bAquí
R (A) es el espacio de imagen de A.
El espacio de imagen es el rango de valores, estoA + A^+A¿Qué significa +? Aún no lo he descubierto.
2. Función indicativa del conjunto convexo.
Dado un conjunto convexo C, su función indicadora es
IC ( x ) = { 0 x ∈ C + ∞ x ∉ C I_C(x)= \begin{cases} 0& \text{x$\in$C}\\ + { \infty}& \text{x$\notin$C} \end{casos}IC( x )={
0+ ∞X∈CX∈/C
Se puede ver que la función conjugada correspondiente es
I c ∗ ( y ) = supx { y T x − IC ( x ) } = supx ∈ C y T x I_c^*(y)=sup_x\{y^Tx-I_C (x) \}=sup_{x{\in}C}y^TxIC∗( y )=sup _ _x{
yT x−IC( x )}=sup _ _x ∈ CyT xaquíIC∗ I_C^
*IC∗También conocido como conjunto convexo CCFunción de soporte de C
3.Norma
La función conjugada de la norma es la función representativa de su esfera unitaria de norma dual, es decir, si f ( x ) = ∣ ∣ x ∣ ∣ f(x)=||x||f ( x )=∣∣ x ∣∣ ,则
f ∗ ( x ) = { 0 ∣ ∣ y ∣ ∣ ∗ ≤ 1 + ∞ ∣ ∣ y ∣ ∣ ∗ > 1 f^*(x)= \begin{cases} 0& \text{
{ $||y||_*$}$\le$1}\\ +{\infty}& \text{ {
$||y||_*$}$>$1} \end{casos}F∗ (x)={
0+ ∞∣∣ y ∣ ∣∗≤1∣∣ y ∣ ∣∗>1

2.6.2 Función conjugada cuadrática
(Función conjugada cuadrática) cualquier función ffLa función conjugada cuadrática de f
se define como f ∗ ∗ ( x ) = supy ∈ domf ∗ sup { x T y − f ∗ ( y ) } f^{**}(x)=sup_{y{\in}domf ^*}sup\{x^Ty-f^*(y)\}F∗∗ (x)=sup _ _y ∈ re o m f∗sup { x _ _
T y−F∗ (y)}
Obviamentef ∗ ∗ f^{**}F*** es siempre una función convexa cerrada (aunque no sé dónde es obvia). A partir de la desigualdad de Fenchel, podemos saber que
f ∗ ∗ ( x ) ≤ f ( x ) , ∀ xf^{**}( x){\le}f( x),{\forall}xF∗∗ (x)≤f(x),∀ x
o equivalente,epif = epif ∗ ∗ epif=epif^{**}e p i f=e p i f***
Teorema: Sifff es una función convexa cerrada, entonces
f ∗ ∗ ( x ) = f ( x ) , ∀ xf^{**}(x)=f(x),{\forall}xF∗∗(x)=f(x),∀x
或等价的, e p i f = e p i f ∗ ∗ epif=epif^{**} epif=epif∗∗
具体的证明这里就不过多阐述了
2.7 次梯度
2.7.1 次梯度的定义
前面介绍了可微函数的梯度,但是对于一般的函数,之前定义的梯度不一定存在,对于凸函数,类比梯度的一阶性质,我们可以引入次梯度的概念
(次梯度)设 f f f为适当凸函数, x x x为定义域 d o m f domf domf中的一点 ,若向量 g ∈ R n g{\in}R^n g∈Rn满足
f ( y ) ≥ f ( x ) + g T ( y − x ) , ∀ y ∈ d o m f f(y){\ge}f(x)+g^T(y-x),{\forall}y{\in}domf f ( y ) ≥ f ( x )+gramoT (y−x ) ,∀ y ∈ d o m f
se llamaggg es la funciónfff en el puntoxxUn subgradiente en x , además, se llama conjunto
∂ f ( \partial}f(x)=\{g|g{\in}R^n,f(y){\ge}f(x)+g^ T(yx),{\forall}y{\in} domf\}∂f ( x ) _={
gramo ∣ gramo ∈ Rnorte ,f ( y ) ≥ f ( x )+gramoT (y−x ) ,∀ y ∈ d o m f }
esfff en el puntoxxSubdiferenciación en
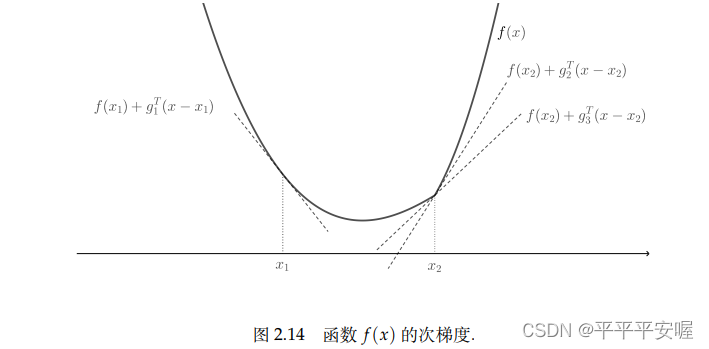
_
_ Siggg esf (x) f(x)f ( x ) atx0x_0_X0subgradiente en , entonces la función
l ( x ) = f ( x 0 ) + g T ( x − x 0 ) l(x)=f(x_0)+g^T(x-x_0)l ( x )=f ( x0)+gramoT (x−X0)
es una función convexaf ( x ) f(x)Un límite inferior global para f ( x ) , además, el subgradienteggg puede inducir la imagen de arribaepif epife p i f en el punto( x , f ( x ) ) (x,f(x))( x ,Un hiperplano de soporte en f ( x ))
La siguiente pregunta es, ¿bajo qué condiciones existe el subgradiente? De hecho, para la función convexa generalffEn términos de f ,ffEs posible que f no tenga subgradientes en todos los puntos, pero para puntos interiores en el dominio,ffEl subgradiente de f
siempre existe.Teorema : Seafff es una función convexa,domf domfd o m f es su dominio, six ∈ intdomfx{\in}intdomfx ∈ en t re o m f , entonces∂ f ( x ) {\partial}f(x)∂ f ( x ) es un subgradiente no vacío
, puedes entenderlo como una función que no es diferenciable en ciertos puntos. En este caso, podemos calcular el conjunto de subgradientes, que representan el rango de todos los gradientes posibles de la función en ese punto.
2.7.2 Propiedades de subgradientes
Función convexa f ( x ) f(x)El subgradiente y la subdiferenciación de f ( x ) tienen muchas propiedades útiles. El siguiente teorema establece que el subdiferencial∂ f ( x ) {\partial}f(x)∂ f ( x )
son respectivamente conjuntos convexos cerrados y conjuntos acotados no vacíos (teorema)bajo ciertas condiciones.f es una función convexa,∂ f ( x ) {\partial}f(x)∂ f ( x ) tiene las siguientes propiedades:
(1) Para cualquierx ∈ domfx{\in}domfx ∈ re o m f,∂ f ( x ) {\partial}f(x)∂ f ( x ) es un conjunto convexo cerrado (posiblemente vacío)
(2) Six ∈ intdomfx{\in}intdomfx ∈ en t re o m f , entonces∂ f ( x ) {\partial}f(x)∂ f ( x ) es un conjunto acotado no vacío
PS: conjunto cerrado: un conjunto que contiene todos sus puntos límite (un conjunto cuyo complemento es un conjunto abierto). La
demostración se omite aquí.
Cuando la función convexa f ( x ) f(x)Cuando f ( x ) es diferenciable en algún punto,∇ f ( x ) {\nabla}f(x)∇ f ( x ) esf ( x ) f(x)El único subgradiente de f ( x )
en este punto es establecerf ( x ) f(x)f ( x )在x 0 ∈ intdomf x_0{\in}intdomfX0∈ en t d o m f es diferenciable, entonces
∂ f ( x 0 ) = { ∇ f ( x 0 ) } {\partial}f(x_0)=\{ { \
nabla}f(x_0)\}∂ f ( x0)={
∇ f ( x0)}
Teorema (monotonicidad de subgradientes): Sea f: R n → R f: R^n{\rightarrow}Rf : Rn →Res una función convexa,x , y ∈ domfx,y{\in}domfx ,y ∈ re o m f,则
( u − v ) T ( x − y ) ≥ 0 (uv)^T(xy){\ge}0( tú−v )T (x−y ) ≥ 0
其中u ∈ ∂ f ( x ) , v ∈ ∂ f ( y ) u{\in}{\partial}f(x),v{\in}{\partial}f(y)tu ∈ ∂ f ( x ) ,La prueba de v ∈ ∂ f ( y )
es bastante fácil
Para funciones convexas cerradas (es decir, funciones semicontinuas convexas), el subgradiente también tiene cierta continuidad.Teorema
: Sea f (x) f(x)f ( x ) es una función convexa cerrada y∂ f ( x ) {\partial}f(x)∂ f ( x ) en el puntoxxexiste y no está vacía cerca de x , si la secuenciaxk → x ˉ x^k{\rightarrow}\bar{x}Xk →Xˉ,gk ∈ ∂ f ( xk ) g^k{\in}{\partial}f(x^k)gramok ∈∂f(xk )esf ( x ) f(x)f ( x ) está en el puntoxkx^kXsubgradiente en k , y gk → g ˉ g^k{\rightarrow}\bar{g}gramok →gramoˉ,则g ˉ ∈ ∂ f ( x ˉ ) \bar{g}{\in}{\partial}f(\bar{x})gramoˉ∈ ∂ f (Xˉ )
demuestra que la continuidad es útil, aquí se omite
2.7.3 Derivadas direccionales de funciones convexas
En fracciones conocemos el concepto de derivadas direccionales, suponiendo fff es una función apropiada, dado un puntox 0 x_0X0y la dirección d ∈ R nd{\in}R^nre ∈ Rn , la derivada direccional (si existe) se define como
lim t ↓ 0 ϕ ( t ) = lim t ↓ 0 f ( x 0 + td ) − f ( x 0 ) t \lim_{t{\downarrow} 0}\ phi(t)=\lim_{t{\downarrow}0}\frac{f(x_0+td)-f(x_0)}{t}t ↓ 0límϕ ( t )=t ↓ 0límtf ( x0+td ) _−f ( x0)
donde t ↓ 0 t{\downarrow}0t ↓ 0 significattt disminuye monótonamente hacia 0, para la función convexaf ( x ) f(x)f ( x ) , es fácil saberϕ ( t ) {\phi(t)}ϕ ( t ) en( 0 , + ∞ ) (0,+{\infty})( 0 ,+∞)上是单调不减的,上述此时极限总是存在(可以为无穷),所以凸函数总是可以定义方向导数
定义(方向导数):对于凸函数 f f f,给定点 x 0 ∈ d o m f x_0{\in}domf x0∈domf以及方向 d ∈ R n d{\in}R^n d∈Rn,其方向导数定义为
∂ f ( x 0 ; d ) = inf t > 0 f ( x 0 + t d ) − f ( x 0 ) t {\partial}f(x_0;d)=\inf_{t>0}\frac{f(x_0+td)-f(x_0)}{t} ∂f(x0;d)=t>0inftf(x0+td)−f(x0)
方向导数可能是正负无穷,但在定义域的内点处方向导数是有限的
即设 f ( x ) f(x) f(x)为凸函数, x 0 ∈ i n t d o m f x_0{\in}intdomf x0∈intdomf,则对任意 d ∈ R n , ∂ f ( x 0 ; d ) d{\in}R^n,{\partial}f(x_0;d) d∈Rn,∂f(x0;d)有限
凸函数的方向导数和次梯度之间有很强的联系,以下结果表明,凸函数 f ( x ) f(x) f(x)关于 d d d的方向导数 ∂ f ( x ; d ) {\partial}f(x;d) ∂f(x;d)正是 f f f在点 x x x处的所有次梯度与 d d d的内积的最大值
定理:设 f : R n → ( − ∞ , + ∞ ] f:R^n{\rightarrow}(-{\infty},+{\infty}] f:Rn→(−∞,+∞]为凸函数,点 x 0 ∈ i n t d o m f x_0{\in}intdomf x0∈intdomf, d d d为 R n R^n Rn中任一方向,则
∂ f ( x 0 ; d ) = max g ∈ ∂ f ( x 0 ) g T d {\partial}f(x_0;d)=\max_{g{\in}{\partial}f(x_0)}g^Td ∂f(x0;d)=g∈∂f(x0)maxgTd _
El teorema anterior se puede aplicar a x ∈ domfx{\in}domf generalx ∈ d o m f se puede generalizar de la siguiente manera:
Teorema: Seafff es una función convexa apropiada y enx 0 x_0X0Cuando el subdiferencial no es un conjunto vacío, entonces para cualquier d ∈ R nd{\in}R^nre ∈ Rn有
∂ f ( x 0 ; d ) = sup g ∈ ∂ f ( x 0 ) g T d {\partial}f(x_0;d)=\sup_{g{\in}{\partial}f(x_0 )}g^Td∂ f ( x0;re )=gramo ∈ ∂ f ( x0)supgramoT d
当∂ f ( x 0 ; d ) {\partial}f(x_0;d)∂ f ( x0;d ) no es infinito, se puede obtener el supremo
2.7.4 Reglas de cálculo para subgradientes
Cómo calcular el subgradiente de una función convexa no diferenciable es una cuestión muy importante en el diseño de algoritmos de optimización. Si el subgradiente se calcula de acuerdo con la definición, generalmente es más engorroso. Introduzcamos algunas reglas de cálculo de subgradiente. Esta sección analiza El valor predeterminado es x ∈ intdomfx{\in}intdomfx ∈ en t re o m f
1. Reglas básicas
Primero damos algunas reglas básicas para calcular subgradientes (subdiferenciales) sin prueba
(1) Funciones convexas diferenciables: Sea fff es una función convexa, sifff en el puntoxxDiferenciable en x , entonces ∂ f ( x ) = { ∇ f ( x ) } {\partial}f(x)=\{ { \
nabla}f(x)\}∂f ( x ) _={
∇ f ( x )}
(2) Combinación lineal no negativa de funciones convexas: Seaf 1 , f 2 f_1,f_2F1,F2为凸函数,且满足
i n t d o m f ! ∩ i n t d o m f 2 ≠ ∅ intdomf_!{\cap}intdomf_2{\not=}{\varnothing} intdomf!∩intdomf2=∅
而 x ∈ i n t d o m f ! ∩ i n t d o m f 2 x{\in}intdomf_!{\cap}intdomf_2 x∈intdomf!∩intdomf2,若
f ( x ) = α 1 f 1 ( x ) + α 2 f 2 ( x ) , α 1 , α 2 ≥ 0 f(x)={\alpha}_1f_1(x)+{\alpha}_2f_2(x),{\alpha}_1,{\alpha}_2{\ge}0 f(x)=α1f1(x)+α2f2(x),α1,α2≥ 0
entoncesf ( x ) f(x)f ( x )的次微分
∂ f ( x ) = α 1 ∂ f 1 ( x ) + α 2 ∂ f 2 ( x ) {\partial}f(x)={\alpha}_1{\partial}f_1( x)+{\alpha}_2{\partial}f_2(x)∂f ( x ) _=a1∂f _1( x )+a2∂f _2( x )
(3) Sustitución de variable lineal: Seahhh es una función apropiada y la funciónfff满足
f ( x ) = h ( A x + b ) , ∀ x ∈ R mf(x)=h(Ax+b),{\forall}x{\in}R^mf ( x )=h ( Un x+segundo ) ,∀ x ∈ Rm
其中A ∈ R n ∗ m , b ∈ R n A{\in}R^{n*m},b{\in}R^nUn ∈ Rnorte ∗ metro,segundo∈Rn , si existex ∗ ∈ R mx^*{\in}R^mX∗ ∈R_m , tal queA x ∗ + b ∈ intdomh Ax^*+b{\in}intdomhuna x∗+b ∈ in t d o mh,则
∂ f ( x ) = AT ∂ h ( A x + b ) , ∀ x ∈ intdomf {\partial}f(x)=A^T{\partial}h(Ax+b ),{\forall}x{\in}intdomf∂f ( x ) _=AT ∂h(Ax+segundo ) ,∀ x ∈ en t d o m f
2. Subgradiente de la suma de dos funciones
Otros M oreau − R ockafellar Moreau-RockafellarMás a ti _−El teorema de R oc ka f e ll a r proporciona el método de cálculo de la subdiferencial de la suma de dos funciones convexas:
Teorema (Moreau-Rockafellar): Seaf 1 , f 2 : R n → ( − ∞ , + ∞ ] f_1 ,f_2 :R^n{\rightarrow}(-{\infty},+{\infty}]F1,F2:Rnorte →(−∞,+ ∞ ] son dos funciones convexas, entonces para cualquierx 0 ∈ R n x_0{\in}R^nX0∈R _n,
∂ f 1 ( x 0 ) + ∂ f 2 ( x 0 ) ⊆ ∂ ( f 1 + f 2 ) ( x 0 ) {\partial}f_1(x_0)+{\partial}f_2(x_0){\subseteq}{\partial}(f_1+f_2)(x_0) ∂f1(x0)+∂f2(x0)⊆∂(f1+f2)(x0)
进一步的,若 i n t d o m f 1 ∩ i n t d o m f 2 ≠ ∅ intdomf_1{\cap}intdomf_2{\not=}{\varnothing} intdomf1∩intdomf2=∅,则对任意的 x 0 ∈ R n x_0{\in}R^n x0∈Rn
∂ ( f 1 + f 2 ) ( x 0 ) = ∂ f 1 ( x 0 ) + ∂ f 2 ( x 0 ) {\partial}(f_1+f_2)(x_0)={\partial}f_1(x_0) +{\parcial}f_2(x_0)∂ ( f1+F2) ( x0)=∂f _1( x0)+∂f _2( x0)
se omite la prueba
3. El supremo de la familia de funciones.
Es fácil verificar que la función suprema de una familia de funciones convexas es una función convexa, tenemos los siguientes resultados importantes:
Teorema (Dubovitskii-Milyutin) Sea f 1 , f 2 , ⋯ , fm : R n → ( − ∞ , + ∞ ] f_1, f_2,\cdots,f_m:R^n{\rightarrow}(-{\infty},+{\infty}]F1,F2,⋯,Fm:Rnorte →(−∞,+∞]均为凸函数,令
f ( x ) = m a x { f 1 ( x ) , f 2 ( x ) , ⋯ , f m ( x ) } , ∀ x ∈ R n f(x)=max\{f_1(x),f_2(x),\cdots,f_m(x)\},{\forall}x{\in}R^n f(x)=max{
f1(x),f2(x),⋯,fm(x)},∀x∈Rn
对 x 0 ∈ ∩ i = 1 m i n t d o m f i x_0{\in}{\cap_{i=1}^m}intdomf_i x0∈∩i=1mintdomfi,定义I ( x 0 ) = { i ∣ fi ( x 0 ) = f ( x 0 ) } I(x_0)=\{i|f_i(x_0)=f(x_0)\}yo ( x0)={
yo ∣ fyo( x0)=f ( x0)},则
∂ f ( x 0 ) = conv ∪ i ∈ I ( x 0 ) ∂ fi ( x 0 ) {\partial}f(x_0)=conv{\cup}_{i{\in}I(x_0 )}{\partial}f_i(x_0)∂ f ( x0)=co n v ∪yo ∈ yo ( x0)∂f _yo( x0)
Se omite la prueba específica y puede que no quede claro qué es conv aquí, de la siguiente manera

4. Valor mínimo de función con componentes fijos
Sea h : R n ∗ R m → ( − ∞ , + ∞ ] h:R^n*R^m{\rightarrow}(-{\infty},+{\infty}]h:Rnorte∗Rmetro →(−∞,+ ∞ ] se trata de( x , y ) (x,y)( x ,y ) , entoncesf ( x ) = inf yh ( x , y ) f(x)=\inf_yh(x,y)f ( x )=en fyh ( x ,y ) es aproximadamentex ∈ R nx{\in}R^nx∈R _ _Función convexa de n , los siguientes resultados se pueden utilizar para resolver fff en el puntoxxUn teorema del subgradiente en x
: considere la función
f ( x ) = inf yh ( x , y ) f(x)=\inf_yh(x,y)f ( x )=yen fh ( x ,y)
其中
h : R n ∗ R m → ( − ∞ , + ∞ ] h:R^n*R^m{\rightarrow}(-{\infty},+{\infty}] h:Rn∗Rm→(−∞,+∞]
是关于 ( x , y ) (x,y) (x,y)的凸函数,对 x ^ ∈ R n \hat{x}{\in}R^n x^∈Rn,设 y ^ ∈ R m {\hat{y}{\in}R^m} y^∈Rm满足 h ( x ^ , y ^ ) = f ( x ^ ) h({\hat{x}},{\hat{y}})=f(\hat{x}) h(x^,y^)=f(x^),且存在 g ∈ R n g{\in}R^n g∈Rn tal que( g , 0 ) ∈ ∂ f ( x ^ ) (g,0){\in}{\partial}f(\hat{x})( g ,0 ) ∈ ∂ f (X^ ),则g ∈ ∂ f ( x ^ ) g{\in}{\partial}f(\hat{x})gramo ∈ ∂ f (X^ )
Para ser honesto, estas cosas son bastante abstractas y puede que sea mucho mejor hacer algunos ejercicios más adelante.
5. Función compuesta
Para el subgradiente de la función compuesta, tenemos el siguiente
teorema de la regla de la cadena: Sea f 1 , f 2 , ⋯ , fm : R n → ( − ∞ , + ∞ ] f_1,f_2,\cdots,f_m:R^n{ \ flecha derecha}(-{\infty},+{\infty}]F1,F2,⋯,Fm:Rnorte →(−∞,+ ∞ ] son m funciones convexas,h : R m → ( − ∞ , + ∞ ] h:R^m{\rightarrow}(-{\infty},+{\infty}]h:Rmetro →(−∞,+ ∞ ] es una función convexa con componentes monótonamente crecientes, sea
f ( x ) = h ( f 1 ( x ) , f 2 ( x ) , ⋯ , fm ( x ) ) f(x)=h(f_1(x ) ,f_2(x),\cdots,f_m(x))f ( x )=h ( f1( x ) ,F2( x ) ,⋯,Fm( x ))
设z = ( z 1 , z 2 , ⋯ , zm ) ∈ ∂ h ( f 1 ( x ^ ) , f 2 ( x ^ ) , ⋯ , fm ( x ^ ) ) z=(z_1,z_2 ,\cdots,z_m){\in}{\partial}h(f_1(\hat{x}),f_2(\hat{x}),\cdots,f_m(\hat{x}))z=( z1,z2,⋯,zm)∈∂h(f1(x^),f2(x^),⋯,fm(x^)),以及 g 1 ∈ ∂ f i ( x ^ ) g_1{\in}{\partial}f_i(\hat{x}) g1∈∂fi(x^),则
g = z 1 g 1 , z 2 g 2 , ⋯ , z m g m ∈ ∂ f ( x ^ ) g=z_1g_1,z_2g_2,\cdots,z_mg_m{\in}{\partial}f(\hat{x}) g=z1g1,z2g2,⋯,zmgm∈∂f(x^)
就是 g g g为 f f f在点 x ^ \hat{x} x^的一个次梯度
感觉就跟正常的链式法则一样
到此为此,第二章基础知识已经过完啦,当然后面的章节肯定会有用到这部分内容的,到时候再回头看巩固一下,第三章是优化建模哦!