Notas introductorias del método de Monte Carlo

Introducción

Principio: De acuerdo con el método de muestreo en el escenario del problema, el sistema se simula a través de una gran cantidad de muestras aleatorias para obtener los parámetros de cálculo requeridos.

Se puede considerar que los métodos de Monte Carlo se dividen aproximadamente en dos categorías. El primer tipo es que el problema a resolver es intrínsecamente aleatorio, y este proceso aleatorio se puede simular directamente con la ayuda de la potencia de cálculo de la computadora. En esta categoría, en la investigación de la física nuclear, el análisis del proceso de transmisión de neutrones en el reactor es un ejemplo más típico. La segunda categoría es que el problema a resolver se puede transformar en una determinada distribución aleatoria de números característicos, como estimar aproximadamente la circunferencia del círculo mediante el método de lanzar puntos, calcular aproximadamente la integral definida, la probabilidad de eventos aleatorios, o el valor esperado de variables aleatorias.

Este artículo se centra en explicar el segundo tipo de situación.

Aproximación de Monte Carlo para encontrar el pi (método de apuntamiento)

import random

def monte_carlo():
    n = 1000000
    r = 1.0
    a, b = (0.0, 0.0)
    x_neg, x_pos = a - r, a + r
    y_neg, y_pos = b - r, b + r

    count = 0
    for i in range(0, n):
        x = random.uniform(x_neg, x_pos)
        y = random.uniform(y_neg, y_pos)
        if x*x + y*y <= 1.0:
            count += 1

    print (count / float(n)) * 4

Monte Carlo Encuentra Integral Definida

Los primeros métodos de Monte Carlo son todos para resolver algunos problemas de suma o integración que no son fáciles de resolver.

Comencemos con un ejemplo simple donde la distribución de probabilidad es uniforme :

Suponiendo que la variable independiente x se distribuye uniformemente entre [a, b], para que


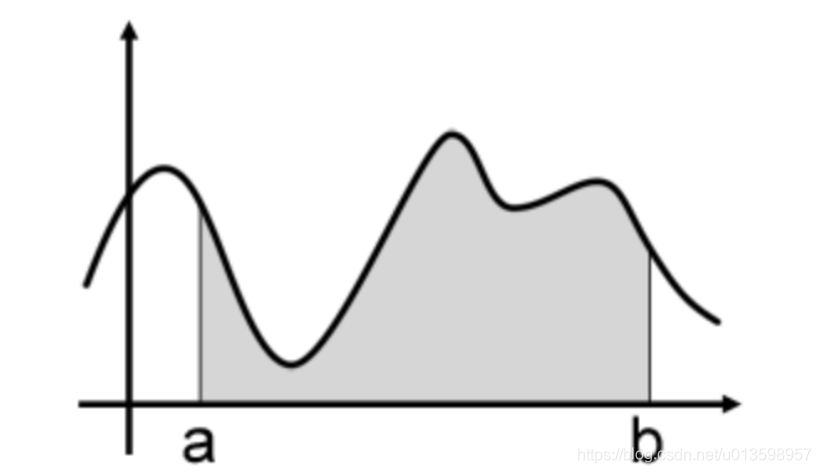
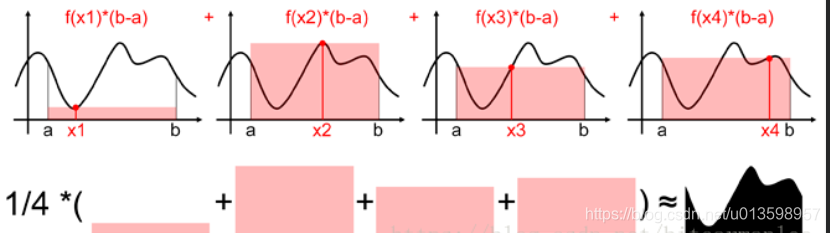
un valor de muestreo (el proceso de muestreo, que se mencionará más adelante) represente todos los valores de f (x) en el intervalo [a, b], la solución es demasiado rugosa. Luego, puede muestrear n valores en el intervalo [a, b]: x0, x1, ... xn − 1, y usar su promedio para representar todos los valores de f (x) en el intervalo [a, b], a saber:

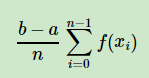
Pero en la mayoría de los casos, la distribución de probabilidad no se distribuye uniformemente.

Si conoce la función de distribución de probabilidad p (x) de x en el intervalo [a, b], la suma se puede realizar así:

esta forma es la forma general del método de Monte Carlo. (La forma de función continua, pero lo mismo se aplica cuando es discreta).

Sustituyendo la condición de distribución uniforme, es decir 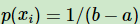, no es difícil encontrar que la distribución uniforme también se puede utilizar como un caso especial de p (x).

Registro simple sobre muestreo

Se obtiene la función de distribución de probabilidad p (x) de x, y luego se puede muestrear un conjunto de muestra que contenga n x que también obedezca a esta distribución en base a ella. ¿Cómo probarlo?

Para el uniforme de distribución uniforme común (0,1) , el muestreo de muestras es fácil. De hecho, se pueden obtener otras distribuciones de probabilidad comunes , ya sean distribuciones discretas o distribuciones continuas, transformando sus muestras a partir de muestras uniformes (0,1) .

Para una distribución que no es una distribución de probabilidad común, un método factible es utilizar un muestreo de aceptación-rechazo para obtener, o una muestra cercana a la distribución. Si p (x) es muy complicado, puede establecer una distribución común q (x) que el programa pueda muestrear, como la distribución gaussiana, y luego rechazar algunas muestras de acuerdo con un método determinado.

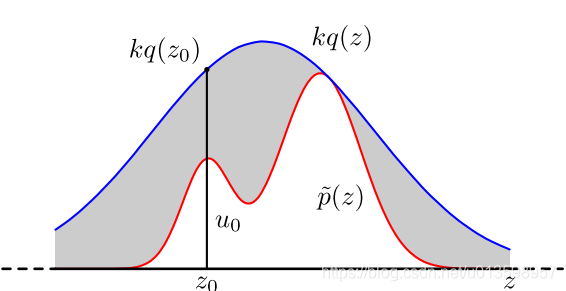
En el ejemplo anterior, primero establezca una distribución gaussiana q (x) y una constante k para que p (x) esté siempre por debajo de kq (x).

A continuación, se muestrea el muestreo conveniente q (x) de acuerdo con el método mencionado anteriormente. Luego, muestrea de la distribución uniforme (0, kq (z0)) para obtener un valor u. Si no cae en el área de distribución real, se rechaza el muestreo. Repita el proceso anterior para obtener n muestras aceptadas: z0, z1, ... zn − 1, finalmente

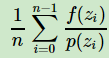
visibles, establezca una distribución fácil de muestrear y luego rechace algunas muestras de acuerdo con un método determinado, para lograr cerca de la distribución de probabilidad real p (x) El propósito de la distribución.

Sin embargo, el muestreo de aceptación-rechazo solo puede satisfacer parcialmente nuestras necesidades.En muchos casos, todavía es difícil obtener un conjunto muestral de distribuciones de probabilidad, como algunas distribuciones bidimensionales ligeramente especiales y distribuciones inusuales de alta dimensión.