Introducción
En la serie anterior de artículos, hablamos sobre el conocimiento relevante y la implementación de los árboles de búsqueda binarios (árbol binario (1) - descripción general (con implementación de árbol de búsqueda binaria) ). Al final del artículo, resumimos la complejidad del tiempo de búsqueda del árbol de búsqueda binaria:
对于一个节点分布相对均衡的二叉查找树来说,如果节点总数是n,那么搜索节点的时间复杂度是O(logn),和树的深度是一样的。
但对于极端情况(每次插入数据大小都是增大的,或者减小的),外形上看就只有一半的树,查找时间复杂度就会退化成O(n)的
Para resolver el problema de la degradación de la complejidad del tiempo de búsqueda del árbol de búsqueda binaria, se necesita el autoequilibrio de los datos binarios, que es de lo que se hablará en esta sección 平衡二叉树. A través de su propio ajuste de balance, las operaciones de búsqueda, inserción y eliminación son O (logn) en el promedio y el peor de los casos. La altura del árbol del árbol de búsqueda binaria afecta la eficiencia de la búsqueda, y la altura del árbol debe reducirse tanto como sea posible. El árbol AVL es uno de esos árboles.
Introducción a los árboles AVL
El árbol binario equilibrado también se llama árbol AVL El nombre del árbol AVL proviene de sus inventores GM Adelson-Velsky y EM Landis. El árbol AVL es el primer árbol de búsqueda binaria autoequilibrado (árbol de búsqueda binaria autoequilibrado, denominado árbol de búsqueda binaria equilibrada) inventado.
Definición de árbol binario equilibrado (AVL):
Es un árbol vacío o un árbol de clasificación binaria con las siguientes propiedades: el valor absoluto de la diferencia (factor de equilibrio) entre las profundidades de sus subárboles izquierdo y derecho no excede 1, y sus subárboles izquierdo y derecho El subárbol es un árbol binario equilibrado.
Un árbol AVL tiene las siguientes condiciones necesarias:
- Debe ser un árbol de búsqueda binaria (consulte el árbol de búsqueda binaria para obtener una definición específica )
- La diferencia de altura entre el subárbol izquierdo y el subárbol derecho de cualquier nodo es como máximo 1.
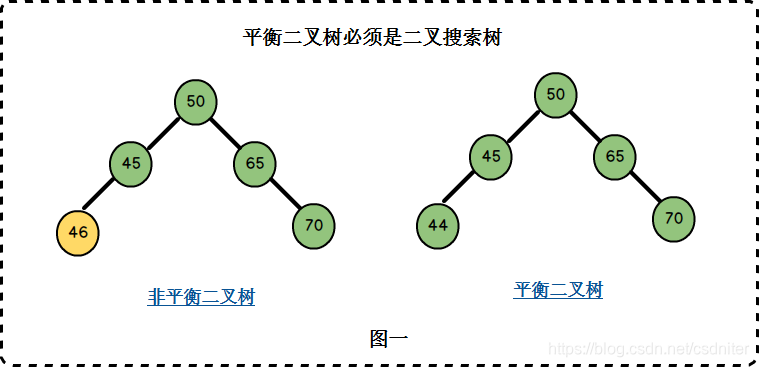
El hijo izquierdo 46 del nodo 45 del árbol binario de la izquierda en la Figura 1 es mayor que 45, lo que no cumple las condiciones del árbol de búsqueda binaria, por lo que no es un árbol binario equilibrado.
El árbol binario de la derecha satisface la condición del árbol de búsqueda binaria y, al mismo tiempo, satisface la condición dos, por lo que es un árbol binario equilibrado.

El nodo 45 del árbol binario de la izquierda tiene una altura del subárbol izquierdo de 2 y una altura del subárbol derecho de 0. La diferencia de altura de los subárboles izquierdo y derecho es 2-0 = 2, lo que no satisface la condición dos;
los nodos del árbol binario de la derecha cumplen como máximo la diferencia de altura de los subárboles izquierdo y derecho 1. Cumple los requisitos de un árbol de búsqueda binario, por lo que es un árbol binario equilibrado.
AVL树的查找、插入、删除操作在平均和最坏的情况下都是O(logn),这得益于它时刻维护着二叉树的平衡。
如果我们需要查找的集合本身没有顺序,在频繁查找的同时也经常的插入和删除,AVL树是不错的选择。
不平衡的二叉查找树在查找时的效率是很低的,因此,AVL如何维护二叉树的平衡是我们的学习重点。
Conceptos relacionados con el árbol AVL
-
平衡因子: El valor de la altura del subárbol izquierdo menos la altura del subárbol derecho del nodo en el árbol binario se denomina factor de equilibrio BF (Factor de equilibrio) del nodo.
En el árbol AVL a la derecha de la Figura 2: la
altura del subárbol izquierdo del nodo 50 es 3, la altura del subárbol derecho es 2, BF = 3-2 = 1; la
altura del subárbol izquierdo del nodo 45 es 2, y la altura del subárbol derecho es 1., BF = 2-1 = 1; la
altura del subárbol izquierdo del nodo 46 es 0, la altura del subárbol derecho es 0, BF = 0-0 = 0; la
altura del subárbol izquierdo del nodo 65 es 0, y la altura del subárbol derecho es 1., BF = 0-1 = -1;
Para un árbol binario balanceado, el rango de valores de BF es [-1,1] . Si encuentra que el valor BF de un nodo no está en este rango, necesita ajustar el árbol. -
最小不平衡子树: El nodo más cercano al nodo insertado y cuyo valor absoluto del factor de balance es mayor que 1 es el subárbol de la raíz.
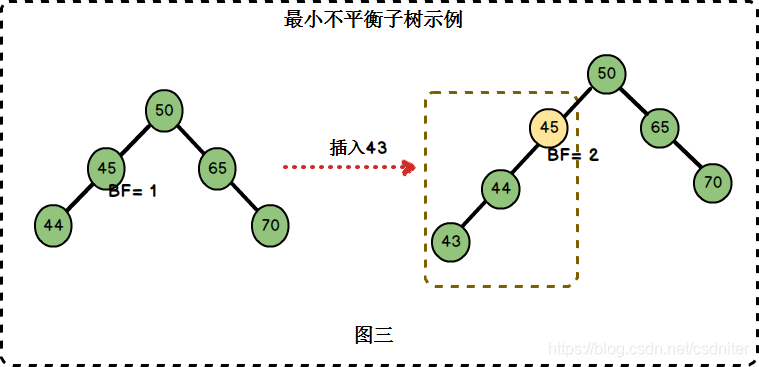
En la Figura 3, el nodo 45 del árbol binario de la izquierda tiene BF = 1. Después de insertar el nodo 43, el nodo 45 tiene BF = 2. El nodo 45 es el nodo cuyo BF más cercano al punto de inserción 43 no está en el rango de [-1,1], por lo que el subárbol enraizado en el nodo 45 es el subárbol desequilibrado más pequeño.
Ajuste de equilibrio del árbol AVL
Cada vez que agrega y elimina elementos, si hay un desequilibrio (a juzgar por el factor de equilibrio), debe realizar una o más rotaciones para ajustar el equilibrio del árbol de acuerdo con la relación de posición entre el nodo recién insertado y el desequilibrio más bajo. nodo.
Hay 4 tipos, tipo LL, tipo RR, tipo LR y tipo RL. Los métodos de ajuste son los siguientes (el nodo desequilibrado más bajo está representado por A a continuación):
Ajuste tipo LL
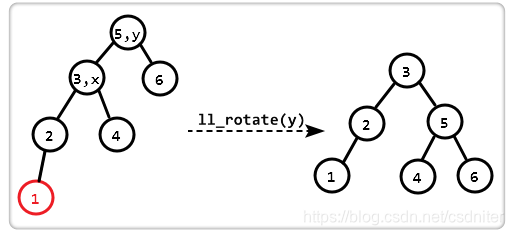
Dado que se inserta un nuevo nodo en el subárbol izquierdo (L) del hijo izquierdo de A (L), el árbol binario equilibrado original se desequilibra. En este momento, el factor de equilibrio de A aumenta de 1 a 2. La Figura 1 a continuación es la forma más simple de tipo LL. Obviamente, de acuerdo con la relación de tamaño, el nodo B debe usarse como el nuevo nodo raíz, y los dos nodos restantes pueden usarse como nodos secundarios izquierdo y derecho para equilibrar. El nodo A es como el nodo B giratorio en sentido horario.
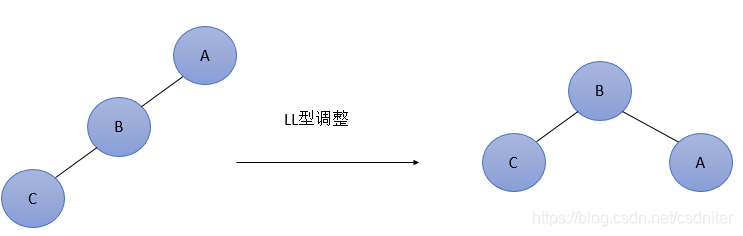
La forma general del ajuste de tipo LL se muestra en la Figura 2 a continuación, lo que significa que un nodo (mostrado en la parte sombreada de la figura) se inserta en el subárbol izquierdo BL (no necesariamente vacío) del hijo izquierdo B de A, lo que resulta en desequilibrio (h significa subárbol La profundidad del árbol). Esta situación se ajusta de la siguiente manera:①将A的左孩子B提升为新的根结点;②将原来的根结点A降为B的右孩子;③各子树按大小关系连接(BL和AR不变,BR调整为A的左子树)。
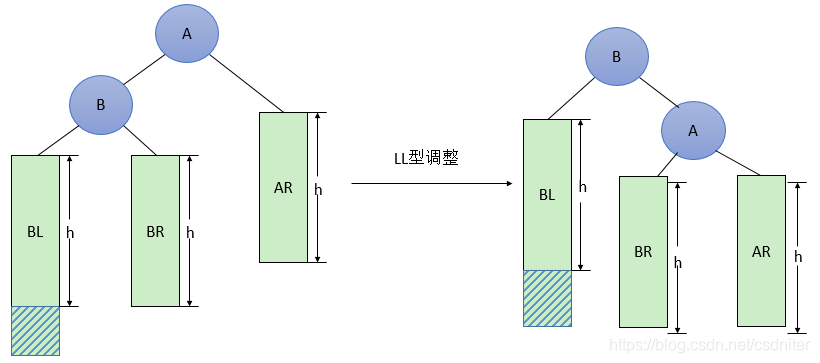
Código:
Ajuste tipo RR
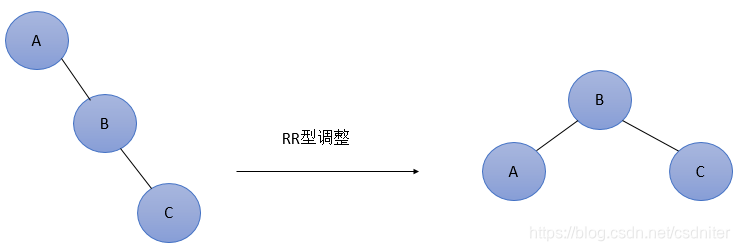
Como resultado de insertar un nuevo nodo en el subárbol derecho del hijo derecho de A, el árbol binario balanceado original se desequilibra En este momento, el factor de balance de A cambia de -1 a -2. La figura 3 es la forma más simple del tipo RR. Obviamente, de acuerdo con la relación de tamaño, el nodo B debe usarse como el nuevo nodo raíz, y los dos nodos restantes pueden usarse como nodos secundarios izquierdo y derecho para equilibrar. El nodo A es como el nodo B giratorio en sentido antihorario.
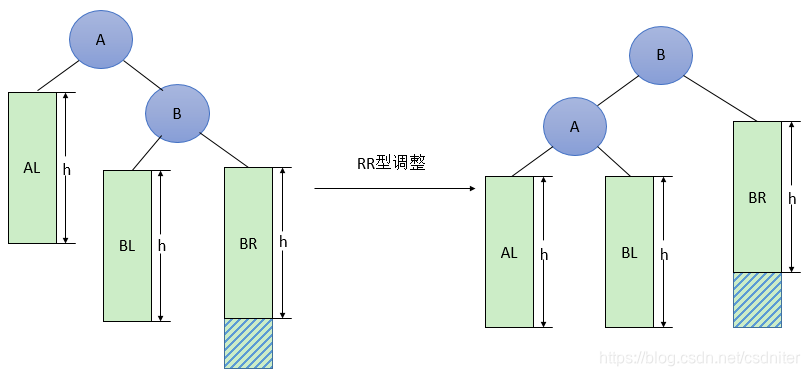
La forma general de ajuste de tipo RR se muestra en la Figura 4 a continuación, lo que significa que un nodo (que se muestra en la parte sombreada de la figura) se inserta en el subárbol derecho BR (no necesariamente vacío) del hijo B derecho de A, lo que resulta en desequilibrio (h significa subárbol La profundidad del árbol). Esta situación se ajusta de la siguiente manera:
- Promocionar al hijo B derecho de A al nuevo nodo raíz;
- Reducir el nodo raíz original A al hijo izquierdo de B
- Los subárboles están conectados de acuerdo con la relación de tamaño (AL y BR permanecen sin cambios y BL se ajusta al subárbol derecho de A).
Código:
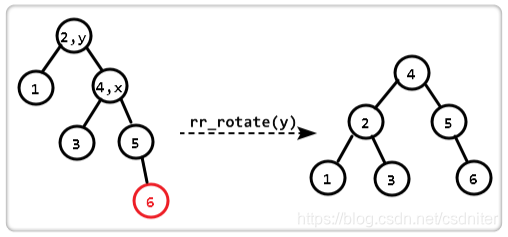
Ajuste tipo LR
Dado que se inserta un nuevo nodo en el subárbol derecho ® del hijo izquierdo de A (L), el árbol binario equilibrado original se desequilibra. En este momento, el factor de equilibrio de A cambia de 1 a 2. La figura 5 es la forma más simple de tipo LR. Obviamente, de acuerdo con la relación de tamaño, el nodo C debe usarse como el nuevo nodo raíz, y los dos nodos restantes se pueden equilibrar como nodos secundarios izquierdo y derecho.
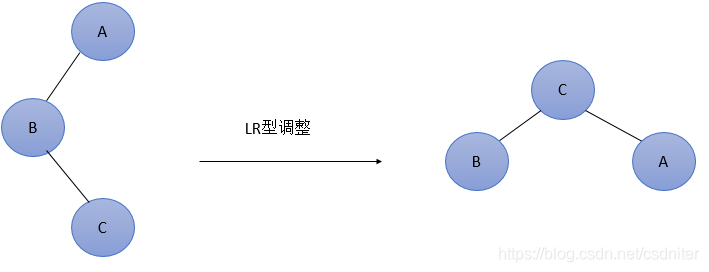
La forma general del ajuste de LR se muestra en la Figura 6 a continuación, lo que significa que un nodo (una de las dos partes sombreadas en la figura) se inserta en el subárbol derecho del hijo izquierdo B de A (el nodo raíz es C, no necesariamente vacío Provoca desequilibrio (h representa la profundidad del subárbol). Esta situación se ajusta de la siguiente manera: ① El hijo izquierdo de B asciende al nuevo nodo raíz; ② El nodo raíz original A se reduce al hijo derecho de C; ③ Los subárboles se conectan de acuerdo con la relación de tamaño (BL y AR permanecen sin cambios, CL y CR se ajustan respectivamente al subárbol derecho de B y al subárbol izquierdo de A).
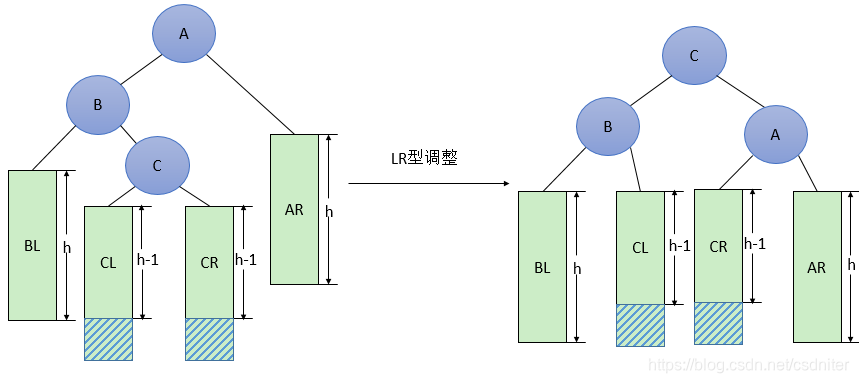
Código:
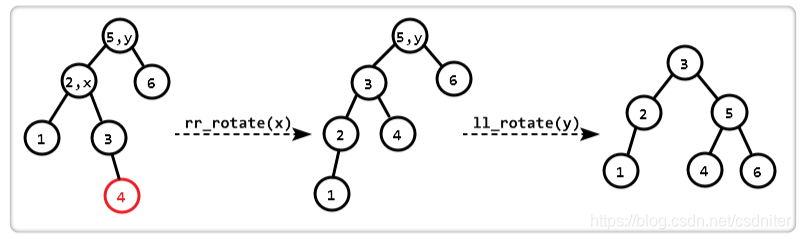
Ajuste tipo RL
Dado que se inserta un nuevo nodo en el subárbol izquierdo (L) del hijo derecho de A, el árbol binario equilibrado original se desequilibra y el factor de equilibrio de A cambia de -1 a -2. La figura 7 es la forma más simple del tipo RL. Obviamente, de acuerdo con la relación de tamaño, el nodo C debe usarse como el nuevo nodo raíz, y los dos nodos restantes se pueden equilibrar como nodos secundarios izquierdo y derecho.
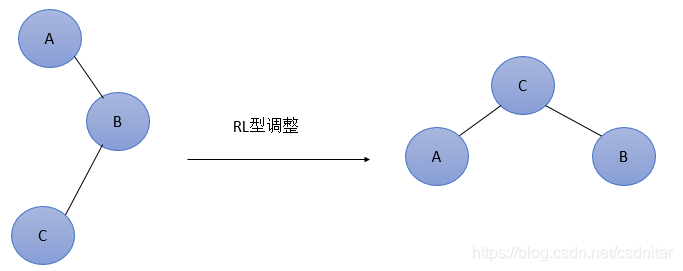
La forma general de ajuste de RL se muestra en la figura siguiente, lo que significa que un nodo (una de las dos partes sombreadas en la figura) se inserta en el subárbol izquierdo del hijo B derecho de A (el nodo raíz es C, no necesariamente vacío ) Desequilibrado (h representa la profundidad del subárbol). Esta situación se ajusta de la siguiente manera: ① El hijo izquierdo C de B asciende al nuevo nodo raíz; ② El nodo raíz original A se reduce al hijo izquierdo de C; ③ Los subárboles se conectan de acuerdo con la relación de tamaño (AL y BR permanecen sin cambios , CL y CR se ajustan respectivamente al subárbol derecho de A y al subárbol izquierdo de B).
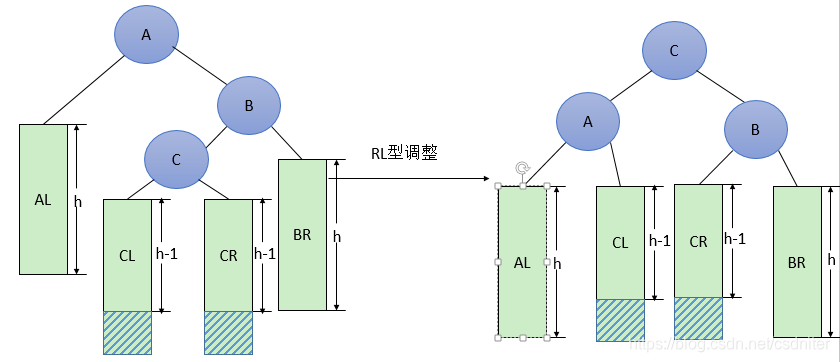
Código:
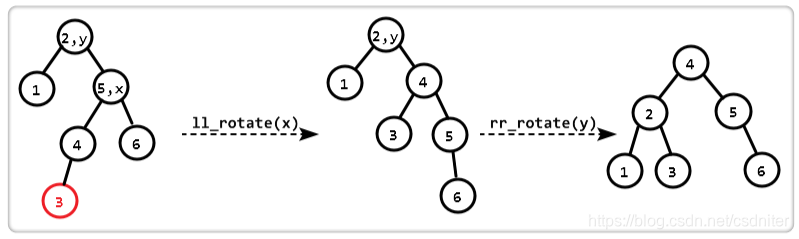
Código
package main
/*
AVL树
*/
import "fmt"
// 平衡二叉树
type AVLTree struct {
RootNode *TreeNode //树的根节点
}
//平衡二叉树节点
type TreeNode struct {
Data int32 // 节点上的数据
Left *TreeNode // 指针指向左孩子节点
Right *TreeNode // 指针指向右孩子节点
Height int // 该节点高度,方便计算平衡因子(相比二叉查找树新增的节点信息,用来判断是否需要进行自平衡调整)
}
// 判断平衡二叉树是否为空树,只需要判断第一个元素是否是 nil
func (self *AVLTree) IsEmpty() bool {
if self.RootNode == nil {
return true
} else {
return false
}
}
// look LL
func left_left_rotation(k *TreeNode) *TreeNode {
var kl *TreeNode
kl = k.Left
k.Left = kl.Right
kl.Right = k
k.Height = max(k.Left.height(), k.Right.height()) + 1
kl.Height = max(kl.Left.height(), k.height()) + 1
return kl
}
//look RR
func right_right_rotation(k *TreeNode) *TreeNode {
var kr *TreeNode
kr = k.Right
k.Right = kr.Left
kr.Left = k
k.Height = max(k.Left.height(), k.Right.height()) + 1
kr.Height = max(k.height(), kr.Right.height()) + 1
return kr
}
//look LR
func left_righ_rotation(k *TreeNode) *TreeNode {
k.Left = right_right_rotation(k.Left)
return left_left_rotation(k)
}
//look RL
func right_left_rotation(k *TreeNode) *TreeNode {
k.Right = left_left_rotation(k.Right)
return right_right_rotation(k)
}
// 取最大值方法
func max(a ...int) int {
if len(a) < 1 {
panic("params count < 1")
}
max := a[0]
for _, i := range a {
if i > max {
max = i
}
}
return max
}
func (node *TreeNode) Add(value int32) *TreeNode {
/*
在平衡二叉树里添加数据
和二叉查找树的插入方法有所不同
二叉查找树Add方法的拥有者是树,平衡二叉树的Add方法拥有者是头节点
因为平衡二叉树在插入数据时需要更新其父代节点的高度,所以要使用递归
*/
if node == nil {
node = &TreeNode{
Data: value}
} else if value < node.Data {
node.Left = node.Left.Add(value)
if node.Left.height()-node.Right.height() == 2 {
if value < node.Left.Data {
//LL
node = left_left_rotation(node)
} else {
// LR
node = left_righ_rotation(node)
}
}
} else if value > node.Data {
node.Right = node.Right.Add(value)
if (node.Right.height() - node.Left.height()) == 2 {
if value < node.Right.Data {
// RL
node = right_left_rotation(node)
} else {
//RR
node = right_right_rotation(node)
}
}
} else if value == node.Data {
fmt.Println("the value", value, "has existed!")
}
//注意:更新高度(可能是不插入旋转值,因此您应该更新高度)
node.Height = max(node.Left.height(), node.Right.height()) + 1
return node
}
//删除指定index节点
//查找节点 ---> 删除节点 ----> 调整树结构
//删除节点时既要遵循二叉搜索树的定义又要符合二叉平衡树的要求 ---> 重点处理删除节点的拥有左右子树的情况
func (node *TreeNode) Delete(value int32) *TreeNode {
//todo
return nil
}
// 这个很关键,和更新节点高度息息相关
func (node *TreeNode) height() int {
if node == nil {
return -1
}
return node.Height
}
// 查找元素所在的节点
func (self *AVLTree) Get(value int32) *TreeNode {
node := self.RootNode
for node != nil {
if value < node.Data {
node = node.Left
} else if value > node.Data {
node = node.Right
} else {
return node
}
}
return nil
}
//前序遍历
func (self *TreeNode) preOrderTraversal(res *[]int32) []int32 {
if self == nil {
return *res
}
*res = append(*res, self.Data)
self.Left.preOrderTraversal(res)
self.Right.preOrderTraversal(res)
return *res
}
func NewAVLTree() *AVLTree {
return new(AVLTree)
}
func main() {
avlTree := NewAVLTree()
data := []int32{
9, 3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8}
for _, value := range data {
avlTree.RootNode = avlTree.RootNode.Add(value)
}
fmt.Println(avlTree.RootNode.Data)
fmt.Println(avlTree.Get(7).height())
var res []int32
fmt.Println(avlTree.RootNode.preOrderTraversal(&res))
}
Referencia:
estructura y algoritmo de datos (implementación de Golang) (28) algoritmo de búsqueda-árbol AVL