Estructura de datos avanzada: árbol binario equilibrado (árbol AVL)

Language 2023-10-03 12:24:45 views: null

Tabla de contenido

1. Estructura subyacente

2. El concepto de números AVL 

3. Definición de nodos del árbol AVL

4. Marco básico

5. Inserción del árbol AVL

6. Rotación del árbol AVL

6.1 Rotación única a la izquierda

6.2 Rotación única derecha

6.3 Doble rotación izquierda y derecha 

6.4 Rotación gemela derecha-izquierda

7. Verificación del árbol AVL

8. Búsqueda del árbol AVL

9. Eliminación del árbol AVL

10. Rendimiento de los árboles AVL

11. código total

11.1 Árbol AVLT

11.2 Prueba.cpp

1. Estructura subyacente

Mapa, mapa múltiple, conjunto y conjunto múltiple se han presentado brevemente antes. Estos contenedores tienen una cosa en común: sus capas inferiores se implementan de acuerdo con árboles de búsqueda binarios , pero los árboles de búsqueda binarios tienen sus propias deficiencias. Si los elementos insertados en el árbol son Ordenado o casi ordenado, el árbol de búsqueda binaria degenerará en un solo árbol y la complejidad del tiempo degenerará en O (N), por lo que la estructura subyacente de contenedores asociativos como map y set es El árbol binario está equilibrado, es decir , se implementa mediante un árbol equilibrado.

2. El concepto de números AVL 

Aunque el árbol de búsqueda binaria puede acortar la eficiencia de la búsqueda, si los datos están ordenados o casi ordenados , el árbol de búsqueda binaria degenerará en un árbol de una sola rama . Buscar elementos equivale a buscar elementos en una tabla de secuencia, lo cual es ineficiente . Por lo tanto, dos matemáticos rusos GMAdelson-Velskii y EMLandis inventaron un método para resolver el problema anterior en 1962: después de insertar un nuevo nodo en el árbol de búsqueda binario, si se pueden garantizar los subárboles izquierdo y derecho de cada nodo. Si el valor absoluto del la diferencia de altura no excede 1 (los nodos en el árbol deben ajustarse), la altura del árbol se puede reducir, reduciendo así la longitud promedio de búsqueda.

Un árbol AVL es un árbol vacío o un árbol de búsqueda binario con las siguientes propiedades:

  1. Sus subárboles izquierdo y derecho son árboles AVL.
  2. El valor absoluto de la diferencia de altura entre cualquier subárbol izquierdo y derecho (conocido como factor de equilibrio) no excede 1 (-1/0/1).
  • 0 significa que las alturas izquierda y derecha son iguales;
  • 1 significa que la altura del subárbol derecho es 1;
  • -1 significa que el subárbol izquierdo tiene una altura de 1.

Si un árbol de búsqueda binario está altamente equilibrado (relativamente equilibrado), es un árbol AVL. Si tiene n nodos, su altura se puede mantener en O(logN) y la complejidad del tiempo de búsqueda es O(logN) .

3. Definición de nodos del árbol AVL

El árbol AVL que implementamos aquí es el modelo KV . Hay dos parámetros de plantilla para los nodos naturales, y el nodo se define como una estructura de conexión trifurcada (hijo izquierdo, hijo derecho, padre). Sobre la base de la lista enlazada binaria, un Se agrega un nodo que apunta al nodo principal. El campo de puntero facilita la búsqueda de nodos secundarios y nodos principales. Luego debe crear una variable _bf como factor de equilibrio (la diferencia de altura entre el subárbol derecho y el subárbol izquierdo). Finalmente, escriba un constructor para inicializar las variables.

//节点类
template<class K, class V>
struct AVLTreeNode
{
	//存储的键值对
	pair<K, V> _kv;
	//三叉连结构
	AVLTreeNode<K, V>* _left;//左孩子
	AVLTreeNode<K, V>* _right;//右孩子
	AVLTreeNode<K, V>* _parent;//父亲
	//平衡因子_bf
	int _bf;//右子树 - 左子树的高度差
	//构造函数
	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _bf(0)
	{}
};

4. Marco básico

El contenido de esta parte es la clase de árbol AVL, su función principal es completar las posteriores operaciones de inserción, rotación y borrado...:

//AVL树的类
template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
    //……
private:
	Node* _root;
};

5. Inserción del árbol AVL

La inserción se divide principalmente en estos pasos principales:

  • 1. El árbol está vacío al principio y se agregan nuevos nodos directamente.
  • 2. Comience con un árbol que no esté vacío y busque una ubicación adecuada para insertarlo.
  • 3. Después de encontrar la posición de inserción adecuada, realice un vínculo bidireccional entre el padre y el niño.
  • 4. Actualice el factor de equilibrio del ancestro del nodo recién insertado.
  • 5. Realizar ajustes rotativos para factores de equilibrio que no cumplan

A continuación, analízalos uno por uno:

  • 1. El árbol está vacío al principio y se agregan nuevos nodos directamente.

Debido a que el árbol está vacío, simplemente cree un nodo recién insertado y utilícelo como raíz _root, luego actualice el factor de equilibrio _bf a 0 y finalmente devuelva verdadero.

  • 2. Comience con un árbol que no esté vacío y busque una ubicación adecuada para insertarlo.

La idea aquí es la misma que la idea de encontrar una posición de inserción adecuada en un árbol de búsqueda binario, y se deben seguir los siguientes pasos:

  1. Valor insertado> valor de nodo, actualizar a la búsqueda del subárbol derecho
  2. Valor insertado <valor de nodo, actualizar a la búsqueda del subárbol izquierdo
  3. Valor insertado = valor de nodo, la inserción de redundancia de datos falla y devuelve falso

Cuando finaliza el bucle, significa que se ha encontrado la ubicación adecuada para la inserción y se puede realizar el siguiente paso de vinculación.

  • 3. Luego de encontrar la posición de inserción adecuada, realizar un vínculo bidireccional entre el padre y el niño:

Tenga en cuenta que el nodo aquí se compone de una cadena de tres vías, por lo que el vínculo final entre el hijo de backend y el padre es un vínculo de dos vías. La operación específica es la siguiente:

  1. Valor insertado> valor del padre, vincule el valor insertado a la derecha del padre
  2. Valor insertado <valor del padre, vincule el valor insertado a la izquierda del padre
  3. Debido a que es un enlace de tres puntas, recuerde tener un enlace de dos vías después de insertarlo (enlaces del niño al padre)

Llegar a este punto significa que el nodo se ha insertado, pero el factor de equilibrio debe actualizarse a continuación.

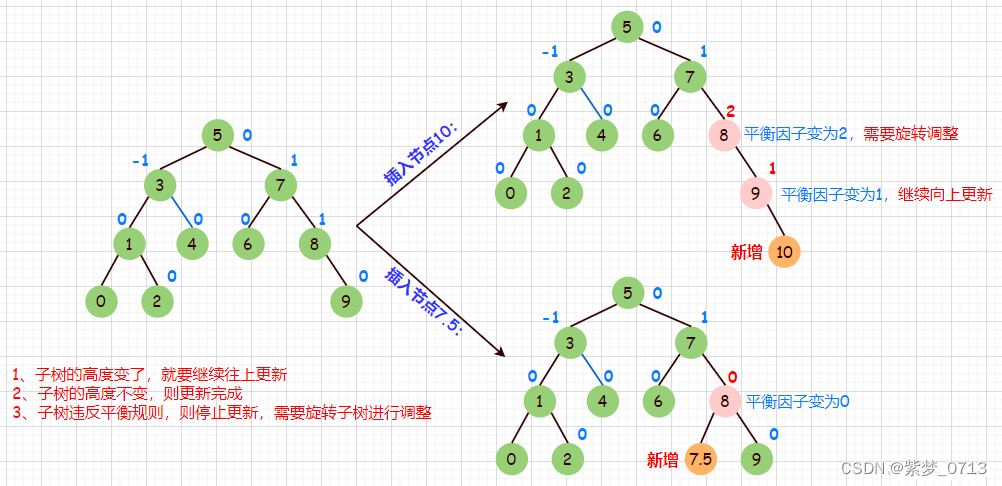
  • 4. Actualice el factor de equilibrio del ancestro del nodo recién insertado:

Cuando insertamos un nuevo nodo, la altura del subárbol puede cambiar, para este cambio damos los siguientes requisitos:

  1. Si la altura del subárbol cambia, debe continuar actualizándose.
  2. Si la altura del subárbol permanece sin cambios, se completa la actualización.
  3. Si el subárbol viola la regla de equilibrio (el valor absoluto del factor de equilibrio >= 2), la actualización se detendrá y será necesario rotar el subárbol para realizar ajustes.

Las reglas de actualización específicas son las siguientes:

  1. El nuevo nodo está a la derecha del padre y el factor de equilibrio del padre es ++ .
  2. El nuevo nodo está a la izquierda del padre y el factor de equilibrio del padre es — — .

Después de actualizar el factor de equilibrio de un nodo, se debe realizar el siguiente juicio:

  1. Si el factor de equilibrio del padre es igual a -1 o 1 (significa que originalmente era 0 , la izquierda y la derecha ascendieron, y el subárbol izquierdo o el subárbol derecho aumentaron después de insertar el nodo). Indica que es necesario continuar actualizando el factor de saldo hacia arriba .
  2. Si el factor de saldo del padre es igual a 0 (significa que originalmente era 1 o -1 , uno alto y otro bajo, y el más corto se completa después de insertar el nodo), significa que no es necesario actualizar el saldo. factor .
  3. Si el factor de equilibrio del padre es igual a -2 o 2 (significa que originalmente era 1 o -1 , uno alto y otro bajo, y el más alto se completa después de insertar el nodo ), significa que el subárbol con el El nodo principal como nodo raíz en este momento ya está desequilibrado y necesita ser rotado .
  • 5. Rotar los ajustes por factores de saldo no conformes:

Cuando el factor de equilibrio del padre es 2 o -2, es necesario realizar un ajuste de rotación y la rotación debe dividirse en las siguientes cuatro categorías:

  1. Cuando el factor de equilibrio del padre es 2 y el factor de equilibrio de cur es 1, se realiza una rotación simple hacia la izquierda.
  2. Cuando el factor de equilibrio del padre es -2 y el factor de equilibrio de cur es -1, realice una rotación única hacia la derecha.
  3. Cuando el factor de equilibrio del padre es -2 y el factor de equilibrio de cur es 1, se realiza una doble rotación hacia la izquierda y hacia la derecha.
  4. Cuando el factor de equilibrio del padre es 2 y el factor de equilibrio de cur es -1, se realiza una doble rotación derecha-izquierda.

El código se muestra a continuación:

//Insert插入
bool Insert(const pair<K, V>& kv)
{
	//1、一开始为空树，直接new新节点
	if (_root == nullptr)
	{
		//如果_root一开始为空树，直接new一个kv的节点，更新_root和_bf
		_root = new Node(kv);
		_root->_bf = 0;
		return true;
	}
	//2、寻找插入的合适位置
	Node* cur = _root;//记录插入的位置
	Node* parent = nullptr;//保存parent为cur的父亲
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			//插入的值 > 节点的值
			parent = cur;
			cur = cur->_right;//更新到右子树查找
		}
		else if (cur->_kv.first > kv.first)
		{
			//插入的值 < 节点的值
			parent = cur;
			cur = cur->_left;//更新到左子树查找
		}
		else
		{
			//插入的值 = 节点的值，数据冗余插入失败，返回false
			return false;
		}
	}
	//3、找到了插入的位置，进行父亲与插入节点的链接
	cur = new Node(kv);
	if (parent->_kv.first < kv.first)
	{
		//插入的值 > 父亲的值，链接在父亲的右边
		parent->_right = cur;
	}
	else
	{
		//插入的值 < 父亲的值，链接在父亲的左边
		parent->_left = cur;
	}
	//因为是三叉连，插入后记得双向链接（孩子链接父亲）
	cur->_parent = parent;
	//4、更新新插入节点的祖先的平衡因子
	while (parent)//最远要更新到根
	{
		if (cur == parent->_right)
		{
			parent->_bf++;//新增结点在parent的右边，parent的平衡因子++
		}
		else
		{
			parent->_bf--;//新增结点在parent的左边，parent的平衡因子 --
		}
		//判断是否继续更新？
		if (parent->_bf == 0)// 1 or -1 -> 0 填上了矮的那一方
		{
			//1 or -1 -》 0 填上了矮的那一方，此时正好，无需更新
			break;
		}
		else if (parent->_bf == 1 || parent->_bf == -1)
		{
			//0 -》 1或-1  此时说明插入节点导致一边变高了，继续更新祖先
			cur = cur->_parent;
			parent = parent->_parent;
		}
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			//1 or -1 -》2或-2 插入节点导致本来高的一边又变更高了
			//此时子树不平衡，需要进行旋转
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				RotateL(parent);//右边高，左单旋
			}
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				RotateR(parent);//左边高，右单旋
			}
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RotateLR(parent);//左右双旋
			}
			else if (parent->_bf == 2 && cur->_bf == -1)
			{
				RotateRL(parent);//右左双旋
			}
			break;
		}
		else
		{
			//插入之前AVL树就存在不平衡树，|平衡因子| >= 2的节点
			//实际上根据前面的判断不可能走到这一步，不过这里其实是为了检测先前的插入是否存在问题
			assert(false);
		}
	}
	return true;
}

6. Rotación del árbol AVL

Hay cuatro tipos de rotación de árboles AVL:

  1. unirotación izquierda
  2. unirotación derecha
  3. doble rotación izquierda y derecha
  4. Doble rotación derecha-izquierda

La rotación del árbol AVL debe seguir los dos principios siguientes:

  • 1. Mantenga las reglas del árbol de búsqueda.
  • 2. El subárbol se equilibra

6.1 Rotación única a la izquierda

  • Condición: el nuevo nodo se inserta a la derecha del subárbol superior derecho

  Hay muchos casos de rotación hacia la izquierda, aquí hacemos un dibujo abstracto para demostrarlo:

Las barras rectangulares (a, b, c) aquí representan el subárbol, h es la altura del subárbol y 30 y 60 son nodos reales. La operación de rotación única izquierda arriba logra principalmente cuatro cosas:

  1. Deje que subRL se convierta en el subárbol derecho del padre y actualice el padre de subRL a padre;
  2. Deje que subR se convierta en el nodo raíz;
  3. Deje que el padre se convierta en el subárbol izquierdo de subR y actualice el padre del padre a subR;
  4. Actualizar factor de saldo.

Aviso:

  1. El padre puede ser un subárbol de todo el árbol, y el padre del padre y el subR deben estar vinculados.
  2. subRL puede estar vacío, pero la actualización del padre de subRL a padre se completa bajo la premisa de que el subRL no está vacío.

Explique por qué la rotación hacia la izquierda anterior es factible:

  • En primer lugar, de acuerdo con la estructura del árbol de búsqueda binario subyacente: el valor del nodo b debe estar entre 30 y 60. No hay problema para que b sea el subárbol derecho de 30, y aquí 60 se mueve a la raíz. y luego 30 se usa como 60 El subárbol derecho de, de modo que el cambio general es como uno hacia la izquierda, y también satisface las propiedades de un árbol de búsqueda binario y está equilibrado de manera uniforme.

El código se muestra a continuación:

void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	Node* ppNode = parent->_parent;//提前保持parent的父亲
	//1、建立parent和subRL之间的关系
	parent->_right = subRL;
	if (subRL)//防止subRL为空
	{
		subRL->_parent = parent;
	}
	//2、建立subR和parent之间的关系
	subR->_left = parent;
	parent->_parent = subR;
	//3、建立ppNode和subR之间的关系
	if (parent == _root)
	{
		_root = subR;
		_root->_parent = nullptr;
	}
	else
	{
		if (parent == ppNode->_left)
		{
			ppNode->_left = subR;
		}
		else
		{
			ppNode->_right = subR;
		}
		subR->_parent = ppNode;//三叉链双向链接关系
	}
	//4、更新平衡因子
	subR->_bf = parent->_bf = 0;
}

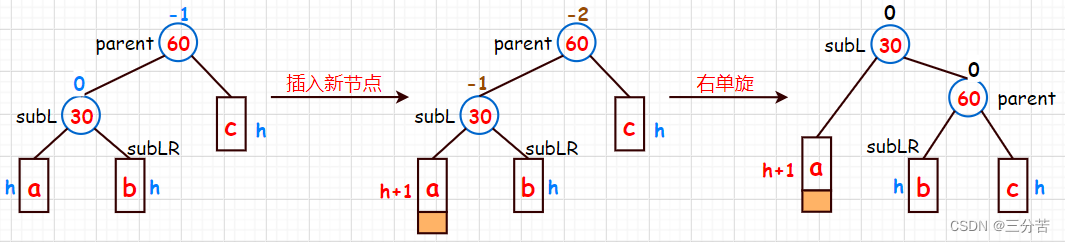
6.2 Rotación única derecha

  •  Condición: el nuevo nodo se inserta a la izquierda del subárbol superior izquierdo

Ilustración:

De manera similar, las barras rectangulares (a, b, c) aquí representan subárboles, h es la altura del subárbol y 30 y 60 son nodos reales. La operación de rotación única izquierda arriba logra principalmente cuatro cosas:

  1. Deje que subLR se convierta en el subárbol izquierdo del padre y actualice el padre de subLR a padre.
  2. Deje que subL se convierta en el nodo raíz
  3. Deje que parent se convierta en el subárbol derecho de subL y actualice el padre de parent a subL.
  4. Actualizar factor de saldo

Aviso:

  1. padre puede ser un subárbol de todo el árbol, y el padre del padre y el subL deben estar vinculados.
  2. subLR puede estar vacío, pero la actualización del padre de subLR a padre se completa bajo la premisa de que subLR no está vacío.

El código se muestra a continuación:
 

//2、右单旋
void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	Node* ppNode = parent->_parent;
	//1、建立parent和subLR之间的关系
	parent->_left = subLR;
	if (subLR)
	{
		subLR->_parent = parent;
	}
	//2、建立subL和parent之间的关系
	subL->_right = parent;
	parent->_parent = subL;
	//3、建立ppNode和subL的关系
	if (parent == _root)
	{
		_root = subL;
		_root->_parent = nullptr;
	}
	else
	{
		if (parent == ppNode->_left)
		{
			ppNode->_left = subL;
		}
		else
		{
			ppNode->_right = subL;
		}
		subL->_parent = ppNode;//三叉链双向关系
	}
	//4、更新平衡因子
	subL->_bf = parent->_bf = 0;
}

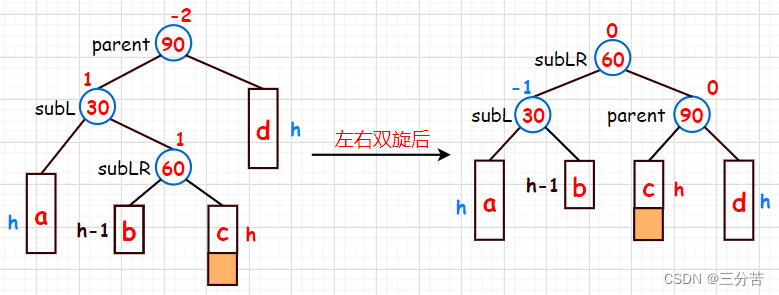
6.3 Doble rotación izquierda y derecha 

  • Condición: el nuevo nodo se inserta a la derecha del subárbol superior izquierdo

El siguiente diagrama ilustra la solución específica de doble rotación izquierda y derecha.

  • 1. Inserte un nuevo nodo:

Este tipo de modelo no satisface las condiciones de rotación simple izquierda ni de rotación simple derecha, pero podemos combinarlas, es decir, doble rotación izquierda y derecha (primero rotación simple izquierda, luego rotación simple derecha) para restablecer el equilibrio. A continuación, realice el siguiente paso de rotación simple hacia la izquierda:

  • 2. Utilice el nodo 30 (subL) como punto de rotación para girar hacia la izquierda:

Observe esta imagen nuevamente en este momento. ¿Es este un modelo monorrotativo del lado derecho adecuado? Considere el subárbol izquierdo de 60 en su conjunto. En este momento, el nodo recién insertado se inserta en el lado izquierdo del subárbol superior izquierdo, que es exactamente De acuerdo con las propiedades de la monorotación hacia la derecha, la monorotación hacia la derecha se puede realizar a continuación:

  • 3. Realice una rotación única hacia la derecha con el nodo 90 (principal) como punto de rotación:

En este momento, se ha completado la doble rotación izquierda y derecha. El último paso es actualizar el factor de equilibrio, pero el factor de equilibrio actualizado se divide en las siguientes tres categorías:

  • 1. Cuando el factor de equilibrio original de subLR es -1, los factores de equilibrio de padre, subL y subLR de los giros dobles izquierdo y derecho se actualizan a 1, 0 y 0 respectivamente.

  •  2. Cuando el factor de equilibrio original de subLR es 1, los factores de equilibrio del padre de doble supinación izquierdo y derecho, subL y subLR se actualizan a 0, -1 y 0 respectivamente.

  •  3. Cuando el factor de equilibrio original de subLR es 0, los factores de equilibrio de padre, subL y subLR de los giros dobles izquierdo y derecho se actualizan a 0, 0 y 0 respectivamente.  

Se puede ver aquí que solo cuando el factor de equilibrio subLR es 0, después de la rotación hacia la izquierda y hacia la derecha, los factores de equilibrio de los tres nodos se actualizarán a 0.

  • El código se muestra a continuación:
//3、左右双旋
void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int bf = subLR->_bf;//提前记录subLR的平衡因子
	//1、以subL为根传入左单旋
	RotateL(subL);
	//2、以parent为根传入右单旋
	RotateR(parent);
	//3、重新更新平衡因子
	if (bf == 0)
	{
		parent->_bf = 0;
		subL->_bf = 0;
		subLR->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = 0;
		subL->_bf = -1;
		subLR->_bf = 0;
	}
	else if (bf == -1)
	{
		parent->_bf = 1;
		subL->_bf = 0;
		subLR->_bf = 0;
	}
	else
	{
		assert(false);//此时说明旋转前就有问题，检查
	}
}

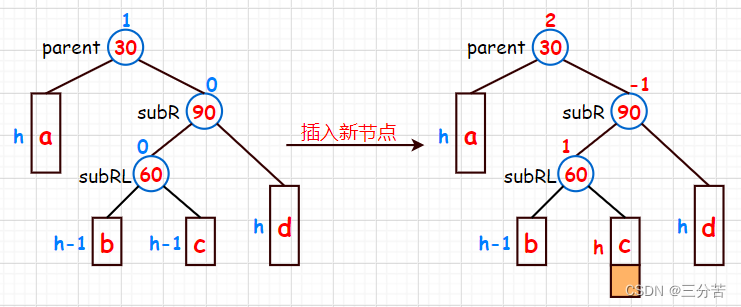
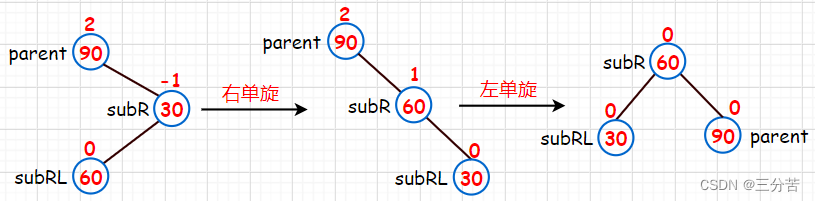
6.4 Rotación gemela derecha-izquierda

  • Condición: el nuevo nodo se inserta a la izquierda del subárbol superior derecho

El siguiente diagrama ilustra la solución específica de doble rotación izquierda y derecha.

  • 1. Inserte un nuevo nodo:

Tenga en cuenta que el nuevo nodo aquí se inserta en el lado izquierdo del subárbol superior derecho. La rotación única y la rotación izquierda y derecha anteriores no se pueden usar. En su lugar, se deben usar la rotación derecha e izquierda (primero una rotación única hacia la derecha, luego una rotación única hacia la izquierda). rotación) para resolver el problema. Luego realice el siguiente paso de rotación a la derecha:

  • 2. Utilice el nodo 90 (subR) como punto de rotación para girar hacia la derecha:

 Observe esta imagen nuevamente en este momento. ¿Es este un modelo apropiado para zurdos? Considere el subárbol derecho de 60 en su conjunto. En este momento, el nodo recién insertado se inserta en el lado derecho del subárbol superior derecho, que es exactamente De acuerdo con las propiedades de la monorotación a la izquierda, la monorotación a la izquierda se puede realizar a continuación:

  • 3. Utilice el nodo 30 (padre) como punto de rotación para girar hacia la izquierda:

En este momento, se ha completado la doble rotación izquierda y derecha. El último paso es actualizar el factor de equilibrio, pero el factor de equilibrio actualizado se divide en las siguientes tres categorías:

  • 1. Cuando el factor de equilibrio original de subRL es -1, los factores de equilibrio de padre, subR y subRL de las supinaciones dobles derecha e izquierda se actualizan a 0, 1 y 0 respectivamente.

  •  2. Cuando el factor de equilibrio original de subRL es 1, los factores de equilibrio de padre, subR y subRL de las supinaciones dobles derecha e izquierda se actualizan a -1, 0 y 0 respectivamente.

  •  3. Cuando el factor de equilibrio original de subRL es 0, los factores de equilibrio de padre, subR y subRL de las supinaciones dobles derecha e izquierda se actualizan a 0, 0 y 0 respectivamente. 

 Se puede ver aquí que solo cuando el factor de equilibrio de subRL es 0, después de la rotación hacia la izquierda y hacia la derecha, los factores de equilibrio de los tres nodos se actualizarán a 0.

  • El código se muestra a continuación:
//4、右左双旋
void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int bf = subRL->_bf;//提前记录subLR的平衡因子
	//1、以subL为根传入左单旋
	RotateR(subR);
	//2、以parent为根传入右单旋
	RotateL(parent);
	//3、重新更新平衡因子
	if (bf == 0)
	{
		parent->_bf = 0;
		subR->_bf = 0;
		subRL->_bf = 0;
	}
	else if (bf == 1)
	{
		parent->_bf = -1;
		subR->_bf = 0;
		subRL->_bf = 0;
	}
	else if (bf == -1)
	{
		parent->_bf = 0;
		subR->_bf = 1;
		subRL->_bf = 0;
	}
	else
	{
		assert(false);//此时说明旋转前就有问题，检查
	}
}

7. Verificación del árbol AVL

El árbol AVL agrega restricciones de equilibrio sobre la base del árbol de búsqueda binario, por lo que para verificar el árbol AVL es ver si es un árbol de búsqueda binario y si es un árbol equilibrado. A continuación discutiremos respectivamente:

  • 1. Verifique que sea un árbol de búsqueda binario:

Aquí solo necesitamos realizar un recorrido en orden para ver si el resultado puede ser una secuencia ordenada. Si es así, se demuestra que es un árbol de búsqueda binario. La implementación del recorrido en orden es muy simple. La implementación anterior del binario El árbol de búsqueda se ha completado. El código se proporciona directamente aquí:

//中序遍历的子树
void _InOrder(Node* root)
{
	if (root == nullptr)
		return;
 
	_InOrder(root->_left);
	cout << root->_kv.first << " ";
	_InOrder(root->_right);
}
//中序遍历
void InOrder()
{
	_InOrder(_root);
	cout << endl;
}

Una vez implementado el código para detectar si es un árbol de búsqueda binario, el siguiente paso es verificar si es un árbol equilibrado.

  • 2. Verificar que sea un árbol equilibrado:

Las reglas son las siguientes: (idea recursiva)

  1. Un árbol vacío también es un árbol equilibrado y hay que juzgarlo desde el principio.
  2. Encapsula una función que calcula específicamente la altura (calcula la altura de forma recursiva) y posteriormente se utiliza para calcular la diferencia de altura (diferencia del factor de equilibrio)
  3. Si la diferencia no es igual al factor de equilibrio de la raíz (root->_bf), o el valor absoluto del factor de equilibrio de la raíz excede 1, no debe ser un árbol AVL.
  4. Continuar recurriendo al subárbol && árbol derecho hasta el final

El código se muestra a continuación:

//验证一棵树是否为平衡树
bool IsBalanceTree()
{
	return _IsBalanceTree(_root);
}
//判读是否平衡的子树
bool _IsBalanceTree(Node* root)
{
	//空树也是AVL树
	if (nullptr == root)
		return true;
	//计算root节点的平衡因子diff：即root左右子树的高度差
	int leftHeight = _Height(root->_left);
	int rightHeight = _Height(root->_right);
	int diff = rightHeight - leftHeight;
	//如果计算出的平衡因子与root的平衡因子不相等，或root平衡因子的绝对值超过1，则一定不是AVL树
	if ((abs(diff) > 1))
	{
		cout << root->_kv.first << "节点平衡因子异常" << endl;
		return false;
	}
	if (diff != root->_bf)
	{
		cout << root->_kv.first << "节点平衡因子与root的平衡因子不等，不符合实际" << endl;
		return false;
	}
	//继续递归检测，直到结束
	return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
//求高度的子树
int _Height(Node* root)
{
	if (root == nullptr)
		return 0;
	int lh = _Height(root->_left);
	int rh = _Height(root->_right);
	return lh > rh ? lh + 1 : rh + 1;
}

Combinando los dos pasos anteriores, puede verificar completamente si un árbol es un árbol AVL.

8. Búsqueda del árbol AVL

La idea de la función Buscar es muy simple: defina el puntero cur para recorrer desde la raíz de acuerdo con las siguientes reglas:

  1. Si el valor de la clave es menor que el valor del nodo actual, la búsqueda debe realizarse en el subárbol izquierdo del nodo.
  2. Si el valor de la clave es mayor que el valor del nodo actual, la búsqueda debe realizarse en el subárbol derecho del nodo.
  3. Si el valor de la clave es igual al valor del nodo actual, la búsqueda es exitosa y se devuelve verdadero.
  4. Si cur atraviesa un círculo y llega a nullptr, significa que no existe tal nodo y devuelve falso.
//Find查找
bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			cur = cur->_right;//若key值大于当前结点的值，则应该在该结点的右子树当中进行查找。
		}
		else if (cur->_key > key)
		{
			cur = cur->_left;//若key值小于当前结点的值，则应该在该结点的左子树当中进行查找。
		}
		else
		{
			return true;//若key值等于当前结点的值，则查找成功，返回true。
		}
	}
	return false;//遍历一圈没找到返回false
}

9. Eliminación del árbol AVL

Simplemente bórralo y descúbrelo.

Dado que los árboles AVL también son árboles de búsqueda binarios, existen tres ideas principales:

  1. Eliminar según las reglas del árbol de búsqueda binaria.
  2. Actualizar factor de saldo
  3. Hay un desequilibrio y se requiere un ajuste de rotación.

Sin embargo, a diferencia de la eliminación de un árbol binario de búsqueda, el factor de equilibrio después de eliminar un nodo debe actualizarse constantemente y, en el peor de los casos, debe ajustarse a la posición del nodo raíz. No lo implementaré específicamente aquí porque es un poco complicado. Sin embargo, hay explicaciones detalladas en los dos libros "Introducción a los algoritmos" o "Estructura de datos: descripción mediante métodos orientados a objetos y C++" publicados por Yin Renkun.

10. Rendimiento de los árboles AVL

El árbol AVL es un árbol de búsqueda binario absolutamente equilibrado, que requiere que el valor absoluto de la diferencia de altura entre los subárboles izquierdo y derecho de cada nodo no exceda 1. Esto garantiza una complejidad del tiempo de consulta eficiente, es decir, O (logN ) . Sin embargo, si desea realizar algunas modificaciones estructurales en el árbol AVL, el rendimiento es muy bajo, por ejemplo, al insertar, debe mantener su equilibrio absoluto y el número de rotaciones es relativamente alto, lo que es aún peor es que al borrar, es posible continuar la rotación hasta la posición de la raíz. Por lo tanto: si necesita una estructura de datos con consulta y orden eficientes, y la cantidad de datos es estática (es decir, no cambiará), puede considerar el árbol AVL, pero si una estructura se modifica con frecuencia, no es adecuada. .

11. código total

11.1 Árbol AVLT

#pragma once
#include<queue>
#include<vector>
#include<iostream>
using namespace std;
//节点类
template<class K, class V>
struct AVLTreeNode
{
	//存储的键值对
	pair<K, V> _kv;
	//三叉连结构
	AVLTreeNode<K, V>* _left;//左孩子
	AVLTreeNode<K, V>* _right;//右孩子
	AVLTreeNode<K, V>* _parent;//父亲
	//平衡因子_bf
	int _bf;//右子树 - 左子树的高度差
	//构造函数
	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};
//AVL树的类
template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	//1、按照搜索树的规则插入
	//2、是否违反平衡规则，如果违反就需要处理：旋转
	bool Insert(const pair<K, V>& kv)
	{	
		//1、一开始为空树，直接new新节点
		if (_root == nullptr)
		{
			//如果_root一开始为空树，直接new一个kv的节点，更新_root和_bf
			_root = new Node(kv);
			_root->_bf = 0;
			return true;
		}
		//2、寻找插入的合适位置
		Node* cur = _root;//记录插入的位置
		Node* parent = nullptr;//保存parent为cur的父亲
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				//插入的值 > 节点的值
				parent = cur;
				cur = cur->_right;//更新到右子树查找
			}
			else if (cur->_kv.first > kv.first)
			{
				//插入的值 < 节点的值
				parent = cur;
				cur = cur->_left;//更新到左子树查找
			}
			else
			{
				//插入的值 = 节点的值，数据冗余插入失败，返回false
				return false;
			}
		}
		//3、找到了插入的位置，进行父亲与插入节点的链接
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			//插入的值 > 父亲的值，链接在父亲的右边
			parent->_right = cur;
		}
		else
		{
			//插入的值 < 父亲的值，链接在父亲的左边
			parent->_left = cur;
		}
		//因为是三叉连，插入后记得双向链接（孩子链接父亲）
		cur->_parent = parent;
		//4、更新新插入节点的祖先的平衡因子
		while (parent)//最远要更新到根
		{
			if (cur == parent->_right)
			{
				parent->_bf++;//新增结点在parent的右边，parent的平衡因子++
			}
			else
			{
				parent->_bf--;//新增结点在parent的左边，parent的平衡因子 --
			}
			//判断是否继续更新？
			if (parent->_bf == 0)// 1 or -1 -> 0 填上了矮的那一方
			{
				//1 or -1 -》 0 填上了矮的那一方，此时正好，无需更新
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				//0 -》 1或-1  此时说明插入节点导致一边变高了，继续更新祖先
				cur = cur->_parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//1 or -1 -》2或-2 插入节点导致本来高的一边又变更高了
				//此时子树不平衡，需要进行旋转
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);//右边高，左单旋
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);//左边高，右单旋
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);//左右双旋
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);//右左双旋
				}
				break;
			}
			else
			{
				//插入之前AVL树就存在不平衡树，|平衡因子| >= 2的节点
				//实际上根据前面的判断不可能走到这一步，不过这里其实是为了检测先前的插入是否存在问题
				assert(false);
			}
		}
		return true;
	}
//求一棵树的高度
	int Height()
	{
		return _Height(_root);
	}
//验证是否为一颗搜索二叉树
	void InOrder()
	{
		_InOrder(_root);//调用中序遍历子树
		cout << endl;
	}

//验证一棵树是否为平衡树
	bool IsBalanceTree()
	{
		return _IsBalanceTree(_root);
	}

private:
//1、左单旋
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* ppNode = parent->_parent;//提前保持parent的父亲
		//1、建立parent和subRL之间的关系
		parent->_right = subRL;
		if (subRL)//防止subRL为空
		{
			subRL->_parent = parent;
		}
		//2、建立subR和parent之间的关系
		subR->_left = parent;
		parent->_parent = subR;
		//3、建立ppNode和subR之间的关系
		if (parent == _root)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;//三叉链双向链接关系
		}
		//4、更新平衡因子
		subR->_bf = parent->_bf = 0;
	}
//2、右单旋
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* ppNode = parent->_parent;
		//1、建立parent和subLR之间的关系
		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		//2、建立subL和parent之间的关系
		subL->_right = parent;
		parent->_parent = subL;
		//3、建立ppNode和subL的关系
		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;//三叉链双向关系
		}
		//4、更新平衡因子
		subL->_bf = parent->_bf = 0;
	}
//3、左右双旋
	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;//提前记录subLR的平衡因子
		//1、以subL为根传入左单旋
		RotateL(subL);
		//2、以parent为根传入右单旋
		RotateR(parent);
		//3、重新更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);//此时说明旋转前就有问题，检查
		}
	}
//4、右左双旋
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;//提前记录subLR的平衡因子
		//1、以subL为根传入左单旋
		RotateR(subR);
		//2、以parent为根传入右单旋
		RotateL(parent);
		//3、重新更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);//此时说明旋转前就有问题，检查
		}
	}

	//中序遍历的子树
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first <<" ";
		_InOrder(root->_right);
	}
	//求一棵树的高度的子树
	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int lh = _Height(root->_left);
		int rh = _Height(root->_right);
		return lh > rh ? lh + 1 : rh + 1;
	}
	//判读是否平衡的子树
	bool _IsBalanceTree(Node* root)
	{
		//空树也是AVL树
		if (nullptr == root)
			return true;
		//计算root节点的平衡因子diff：即root左右子树的高度差
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = rightHeight - leftHeight;
		//如果计算出的平衡因子与root的平衡因子不相等，或root平衡因子的绝对值超过1，则一定不是AVL树
		if ((abs(diff) > 1))
		{
			cout << root->_kv.first << "节点平衡因子异常" << endl;
			return false;
		}
		if (diff != root->_bf)
		{
			cout << root->_kv.first << "节点平衡因子与root的平衡因子不等，不符合实际" << endl;
			return false;
		}
		//继续递归检测，直到结束
		return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
	}
public:
	vector<vector<int>> levelOrder() {
		vector<vector<int>> vv;
		if (_root == nullptr)
			return vv;

		queue<Node*> q;
		int levelSize = 1;
		q.push(_root);

		while (!q.empty())
		{
			// levelSize控制一层一层出
			vector<int> levelV;
			while (levelSize--)
			{
				Node* front = q.front();
				q.pop();
				levelV.push_back(front->_kv.first);
				if (front->_left)
					q.push(front->_left);

				if (front->_right)
					q.push(front->_right);
			}
			vv.push_back(levelV);
			for (auto e : levelV)
			{
				cout << e << " ";
			}
			cout << endl;
			// 上一层出完，下一层就都进队列
			levelSize = q.size();
		}
		return vv;
	}
	
private:
	Node* _root = nullptr;
};

11.2 Prueba.cpp

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
#include<time.h>
#include<assert.h>
using namespace std;
#include"AVLTree.h"

void TestAVLTree1()
{
	int a[] = { 1,2,3,4,5,6,7,8 };
	AVLTree<int, int> t;
	t.Insert(make_pair(1, 1));
	t.Insert(make_pair(2, 2));
	t.Insert(make_pair(3, 3));
}
void TestAVLTree2()
{
	//int a[] = { 1,2,3,4,5,6,7,8 };
	int a[] = { 8,7,6,5,4,3,2,1 };
	AVLTree<int, int> t;
	for (auto e : a)
	{
		t.Insert(make_pair(e, e));
	}
}
void TestAVLTree3()
{
	const size_t N = 1024;
	vector<int> v;
	srand(time(0));
	v.reserve(N);
	for (size_t i = 0; i < N; i++)
	{
		//v.push_back(i);
		v.push_back(rand());
	}
	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
	}
	t.levelOrder();
	cout << endl;
	t.InOrder();
}
void TestAVLTree4()
{
	const size_t N = 1024 * 1024;
	vector<int> v;
	srand(time(0));
	v.reserve(N);
	for (size_t i = 0; i < N; i++)
	{
		v.push_back(i);//有序插入 --》检测单旋是否正确
		//v.push_back(rand());//乱序插入 --》检测双旋是否正确
	}
	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, e));
	}
	cout << "是否平衡？" << t.IsBalanceTree() << endl;
	cout << "高度：" << t.Height() << endl;
	//t.InOrder();//判断是否二叉搜索树
}
int main()
{
	//TestAVLTree1();
	//TestAVLTree2();
	//TestAVLTree3();
	TestAVLTree4();
}

Supongo que te gusta

Origin blog.csdn.net/m0_49687898/article/details/131334137
Recomendado
Clasificación
Diario
Más
2024-05-08(18)
2024-05-07(35)
2024-05-06(4)
2024-05-05(0)
2024-05-04(17)
2024-05-03(8)
2024-05-02(0)
2024-05-01(4)
2024-04-30(33)
2024-04-29(5)

Code World

© 2018 codetd.com