Singular value decomposition SVD (singular value decomposition)

singular value decomposition

SVD is a very useful matrix factorization method.
Purpose proposed by SVD: any $m\times The\; matrices\; of\; n$ can be regarded as a hyperellipse (ellipse in high-dimensional space), and they can be regarded as images of the unit sphere S.
A hyperellipse can be formed by placing the unit sphere in the orthogonal direction ${in}_1,{in}_2,...,{in}_{\mathbf{m}}$By scaling factor$p_1,...,p_m$, where m is the dimension, if m=2 on the plane

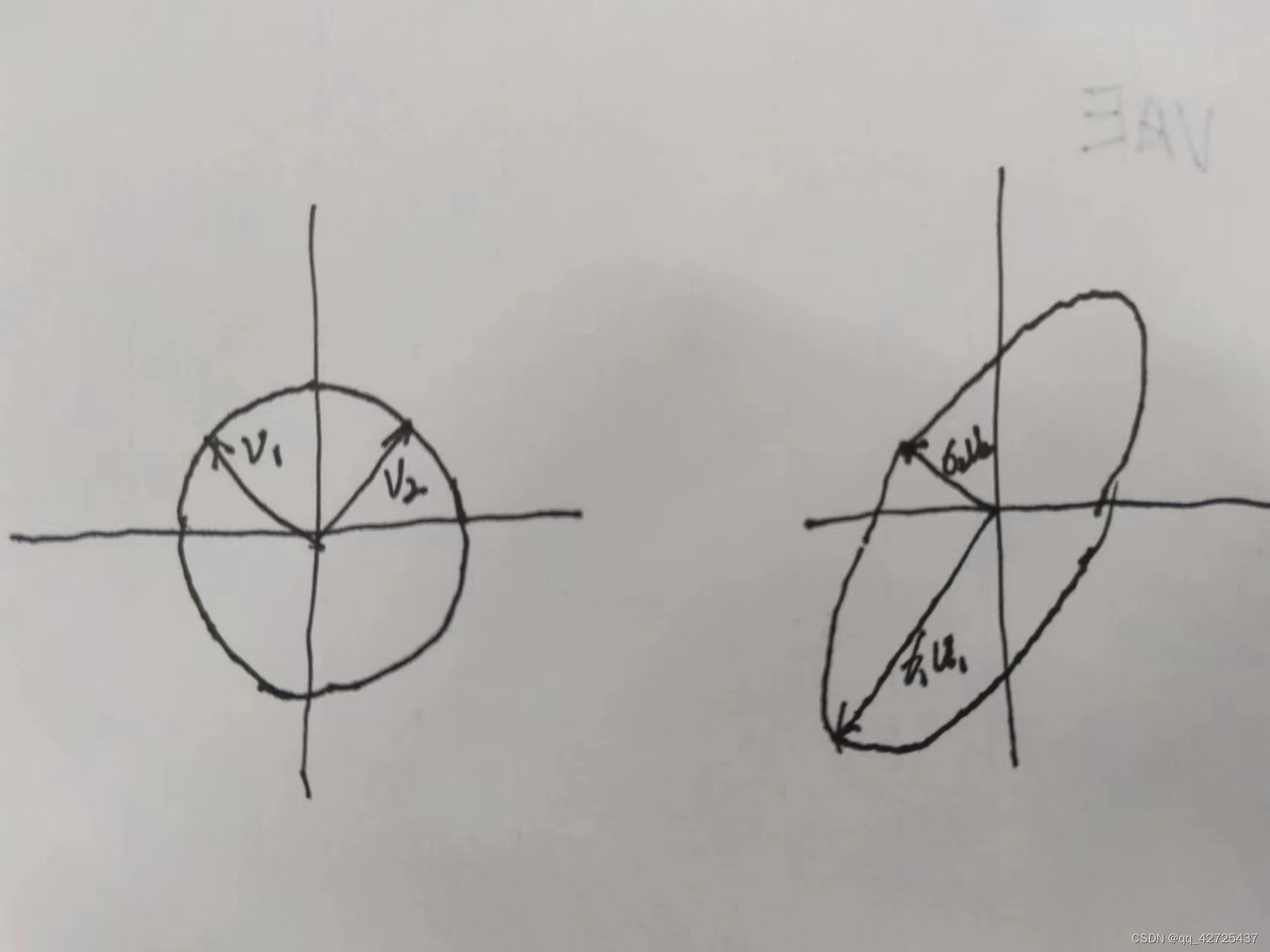
Through the above picture, the following definition can be made:

1. singular value:$p_1,...,p_n\ge 0$Individualization$p_1\ge p_2\ge ...$
2. Light singular vectors:${in}_1,{in}_2,...,{in}_n$,unit vector
3. right singular vectors:${in}_1,{in}_2,...,{in}_n$This is ui's opposite direction$A{v}_i=p_i{in}_i$
   The left and right names come from the formula of svd.
   By matrixing the above formula, we can get:
   $$AV=\widehat{IN}\hat{S}$$
   Zairi-myeon
4. $\hat{S}\in {\mathbb{R}}^{n\times n}$ is a non-negative diagonal matrix
5. $\widehat{IN}\in R^{m\times n}$is one straight orthogonal square
6. $IN\in R^{n\times n}$ is a column orthogonal matrix
   Therefore V is an orthogonal matrix, because it is a basis vector, so we can get reduced SVD:
   $$A=\widehat{IN}\hat{S}{V}^T$$
   Just like QR decomposition, the expansion $\widehat{IN}$的列使得$IN\in R^{m\times m}$
   then demand line$\hat{S}$Add some rows with a value of 0 so that the newly added random columns in U can be silenced, thus obtaining a complete SVD
   $$A=U\Sigma V^T$$
   Comparing reduced and full
   
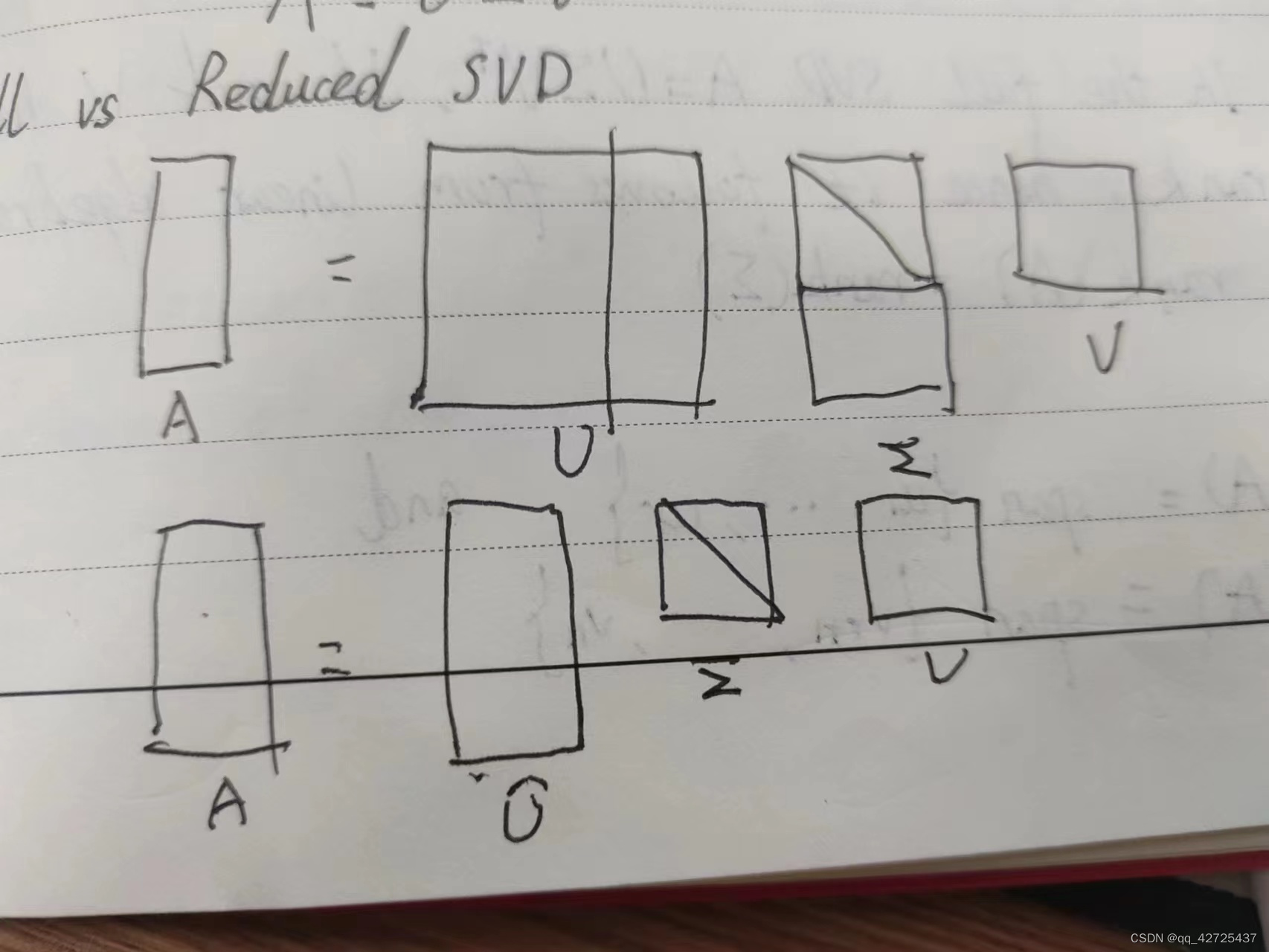
   Now reconsider the purpose of changing the spherical shape into a super elliptical shape.
   1 ${IN}^T$是球型S
   2 $\Sigma$La extended ball type obtained to reach spherical shape
   3 $U$Rotate projection without changing shape

You can know some matrix properties through SVD

1. The rank of A is r, which is the number of non-zero singular values
   Proof: U and V are of full rank, so rank(A) = rank($\Sigma$)
2. image(A) = span{ the 1 , the 2 , . . . , u r \mathbf{u_1},\mathbf{u_2},...,\mathbf{u_r} ${in}_1,{in}_2,...,{in}_{\mathbf{r}}$}
   null(A) = span{ v r + 1 , . . . , v n \mathbf{v_{r+1}},...,\mathbf{v_n} ${in}_{\mathbf{r}+1},...,{in}_n$}
3. $||A|{|}_2=p_1$
   proof:$||A|{|}_2\equiv at{x}_{||V|{|}_2=1}$||Off||_2
4. The singular value of A is the square root of the eigenvalue of AAT.
   According to the above properties: we can know two applications of SVD

Condition number of rectangular matrix

$K(A)=||A||||A^{+}||$
inside$A^{+}$This is the opposite

• $||A|{|}_2=p_{atx}$
• $||A^{+}|{|}_2=\frac{1}{p_{min}}$
  所以$K\left(A\right)=\frac{p_{atx}}{p_{min}}$

low rank approximation

把SVD变为
$$A=\sum _{j=1}^r{p}_j{in}_j{in}_j^T$$
每个${in}_j{in}_j^T$ is a matrix of rank 1
Theorem:
for$0\le in\le A\; v\; =\; \sum \; j\; =\; 1\; v\; \sigma \; j\; u\; j\; v\; j\; T\; Av\; =\; \backslash sum^v\_\{j=1\}\backslash sigma\_ju\_jv\_j\; ^T$$Av={\sum }_{j=1}^v{p}_j{in}_j{in}_j^T$
所以
$$||A-Av|{|}_2=\underset{B\in {\mathbb{R}}^{m\times n},rank(B)\le v}{\inf }||A-B|{|}_2$$
The same can also be proved in Frobenius norm. This theory shows that SVD is a good method for compressing matrices.