Understand the principle and application of Singular Value Decomposition (SVD) in one article

The following content refers to the study notes of Zhihu Singular Value Decomposition (SVD) and Singular Value Decomposition (SVD) of Matrix Analysis , summarized as follows:

1 Introduction

Singular Value Decomposition (SVD) is an algorithm widely used in the field of machine learning. It is a powerful tool for extracting information. It provides a very convenient way of matrix decomposition and can find interesting data in the data . potential model. This article makes an introduction to the principle of SVD and gives a practical use case.

2 Eigenvalues ​​and eigenvectors

Before doing SVD derivation, let’s understand the definition of eigenvalues ​​and eigenvectors:
$$Ax=\lambda x$$

where A is an $n\times$matrix of$n$$x$ is an n-dimensional vector, then$\lambda$ is an eigenvalue of matrix A, and$x$ is the eigenvalueλ \lambdaThe eigenvector corresponding to$\lambda \; .$

What are the benefits of finding eigenvalues ​​and eigenvectors? That is, we can decompose the matrix A into eigenvalues.

That is to say, the information of matrix A can be represented by its eigenvalues ​​and eigenvectors.

If we find the n eigenvalues ​​of matrix A $l_1\le l_2\le ...\le l_n$, and the eigenvectors $w_1,w_2,...,w_n$ ，

Then the matrix A can be represented by the eigendecomposition of the following formula: where W is the n × nn\times n

spanned by these n eigenvectors$n\times n$ -dimensional matrix, and Σ is the n × nn\times nof the main diagonal of these n eigenvalues$n\times n-$ dimensional matrix.

Generally, we will standardize the n eigenvectors of W, that is, satisfy ${\left|\left|w_i\right|\right|}_2=1$，orwi$w_i^T{w}_i=1$ , at this time the n eigenvectors of W are orthonormal bases, satisfying$W^{T}W=I$ ，即 $W^T=W^{-1}$ , that is to say, W is a unitary matrix.

Orthogonal Matrix (Orthogonal Matrix) refers to the matrix whose transpose is equal to its inverse $A^T=A^{-1}$
unitary matrix is ​​the generalization of the orthogonal matrix to the field of complex numbers

In this way, our eigendecomposition expression can be written as

Summarize, eigenvalue decomposition can obtain eigenvalues ​​and eigenvectors, eigenvalues ​​indicate how important this feature is, and eigenvectors indicate what this feature is. However, eigenvalue decomposition also has many limitations, for example, the transformed matrix must be a square matrix .

3 SVD decomposition

Eigenvalue decomposition is a very good method to extract matrix features, but it is only for square matrices. In the real world, most of the matrices we see are not square matrices. For example, there are M students, each Students have grades in N subjects, so an M*N matrix A cannot be a square matrix. How can we describe the important characteristics of such an ordinary matrix? Singular value decomposition is a decomposition method that can be applied to any matrix:

where U is a $m\times The\; matrix\; of\; m$ ,$\Sigma$ is a$m\times The\; matrix\; of\; n$ is all 0 except for the elements on the main diagonal. Each element on the main diagonal is called a singular value. V is an$n\times$matrix of$n\; .$Both U and V are unitary matrices, which satisfy:

$$U^{T}U=I,V^{T}V=The$$
following figure can clearly see the definition of SVD above:

So how do we find the three matrices U, Σ, and V after SVD decomposition?

If we do matrix multiplication with the transpose of A and A, then we get $n\times$A square matrixATAA^{T}A$of\; n$$A^{T}A$_$A^{T}A$is a square matrix, then we can perform eigendecomposition, and the obtained eigenvalues ​​and eigenvectors satisfy the following formula:

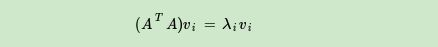
In this way, we can get the matrix$A^{The\; n\; eigenvalues\; of\; T}A$and the corresponding n eigenvectors v. will$A^{}$All the eigenvectors of${}^T$$A$$n\times The\; matrix\; V\; of\; n$ is the V matrix in our SVD formula. Generally we call each eigenvector in Vtheright singular vector

If we do matrix multiplication of A and the transpose of A, we get $m\times$A square matrixAAT AA^{T}$of\; m$$A{A}^{T.}$ _ Since$A{A}^T$ is a square matrix, then we can perform eigendecomposition, and the obtained eigenvalues ​​and eigenvectors satisfy the following formula:

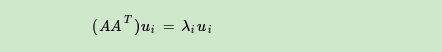
In this way, we can get the matrix$A{A}^{The\; m\; eigenvalues\; of\; T}$ and the corresponding m eigenvectors u. will$A{A}^{}$All the eigenvectors of${}^T$$m\times The\; matrix\; U\; of\; m$ is the U matrix in our SVD formula. Generally we call each eigenvector in Utheleft singular vector

We have obtained both U and V, and now there is only the singular value matrix Σ that has not been obtained. Since Σ is 0 except for the singular value on the diagonal, then we only need to obtain each singular value σ. OK.

We noticed:

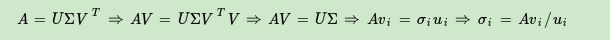
In this way we can find each of our singular values, and then find the singular value matrix Σ.

There is one more question that was not mentioned above, that is, we said $A^{The\; eigenvectors\; of\; T}A$form the V matrix in our SVD, and$A{A}^{}$The eigenvector of${}^{T\; is\; the\; U\; matrix\; in\; our\; SVD.\; Is\; there\; any\; basis\; for\; this?}$This is actually very easy to prove. Let's take the proof of the V matrix as an example.

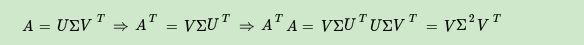
The above formula proves that$U^U=I,S^T=\Sigma$ . It can be seen that$A^{}$The eigenvectors of${}^T$$A$A similar method can get$A{A}^{The\; eigenvectors\; of\; T}$ form the U matrix in our SVD.

Further, we can also see that our eigenvalue matrix is ​​equal to the square of the singular value matrix, which means that the eigenvalues ​​and singular values ​​satisfy the following relationship: In other words,

we can use $p_i=\frac{A{v}_i}{u_i}$To calculate the singular value, you can also find $A^{}$Take the square rootof the eigenvalues ​​of${}^T$$A$to find the singular values.

4 SVD Calculation Example

For the singular value of matrix A, we can first calculate it through wolframalpha:

manual calculation steps:

Singular Value Decomposition (SVD) of Matrix Analysis
https://www.bilibili.com/video/av15971352/?p=5

As shown in the figure above, we can see that SVD can divide the matrix into different matrices and add them together, and the coefficients in front of the division are the SVD values. For the singular value, it is similar to the eigenvalue in our eigendecomposition, and it is also in the singular value matrix. Arranged from large to small, and the singular values ​​decrease very fast. In many cases, the sum of the top 10% or even 1% of the singular values ​​accounts for more than 99% of the total sum of the singular values.

In other words, we can also use the largest k singular values ​​and the corresponding left and right singular vectors to approximate the description matrix.

Due to this important property, SVD can be used for PCA dimension reduction for data compression and denoising , and can also be used for recommendation algorithms to decompose the matrix corresponding to users and preferences, and then obtain implicit user needs for recommendation .

5 SVD for PCA

PCA dimensionality reduction, need to find the sample covariance matrix $X^{The\; largest\; d\; eigenvectors\; of\; T}X$, and then use the matrix formed by the largest d eigenvectors to perform low-dimensional projection dimensionality reduction. It can be seen that in this process, the covariance matrix$X^{T}X$, when the number of samples is large and the number of features of samples is large, the amount of calculation is very large.

Note that our SVD can also get the covariance matrix $X^{}$The matrix formed by the largest d eigenvectors of${}^T$$X$$X^{T}X$, can also find our right singular matrix V.

In other words, our PCA algorithm can be done without eigendecomposition, but with SVD. This method is very effective when the sample size is large.

In fact, the real implementation behind scikit-learn's PCA algorithm is to use SVD instead of the violent feature decomposition we think.

On the other hand, notice that PCA only uses the right singular matrix of our SVD, not the left singular matrix, so what is the use of the left singular matrix?

Suppose our sample is $m\times The\; matrix\; X\; of\; n$ , if we find the matrix$X{X}^{}$The m × dm×dspanned by the largest d eigenvectors of${}^T$$m\times d-$ dimensional matrix U, if we proceed as follows:

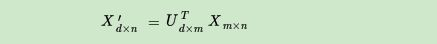
we can get a$d\times The\; matrix\; X\text{'}\; of\; n$ , this matrix and our original$m\times Compared\; with\; the\; n-$ dimensional sample matrix X, the number of rows is reduced from m to k, which shows that the number of rows is compressed.

Left singular matrices can be used to compress the number of rows.

The right singular matrix can be used to compress the number of columns, that is, the feature dimension, which is our PCA dimensionality reduction.

6 Summary

1. SVD decomposition is to decompose a matrix into its left eigenspace matrix and right eigenspace matrix, and the eigenvalue matrix in the middle represents the weight value, so we only need to select those important features and keep them every time. Restore the original matrix with almost no loss;

2. SVD decomposition can be regarded as a low-rank expression of the original matrix ;

3. SVD can be used for data denoising;

4. SVD can be used for feature dimension compression;