[Unity] Unity geometry knowledge, radian, trigonometric functions, vector operations, dot product, cross product

---

basic geometry knowledge

measure of angle

There are two ways to measure angles: degree and radian. Angle is to cut a circle into 360 parts, each part is an angle of 1 degree. One radian is when the arc length is equal to the radius of the circle.

as the picture shows:

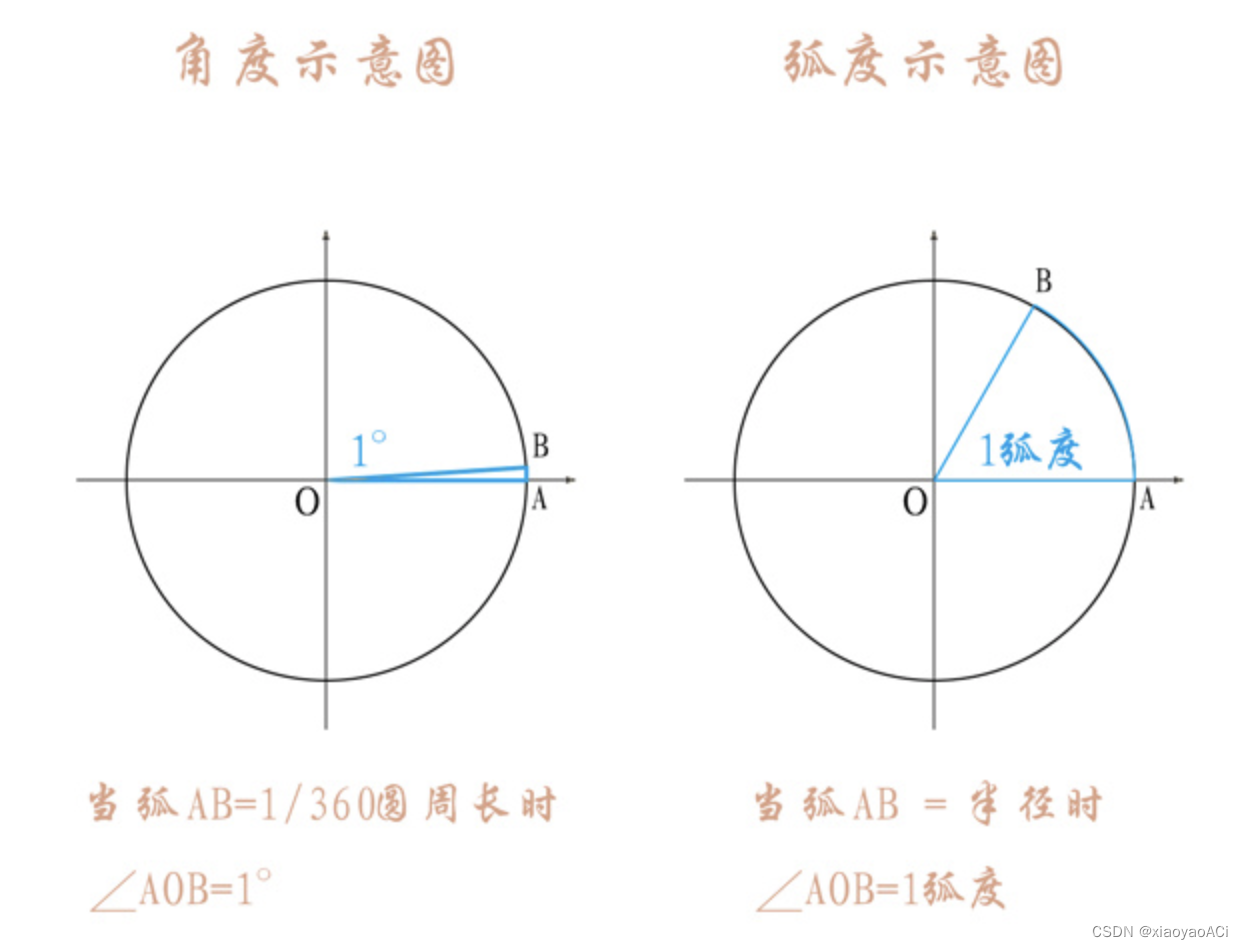
Angle to radian conversion

Common calculation:
$Pi=180degree$
$1arcdegree=180degrees/\pi$
$1angledegree=\pi /180度$

Angle to radian:

• Conversion formula:$arcdegree=AngleDegreeNumber\ast \pi /180$
• Unity code: radian = x * Mathf.Deg2Rad;

Rotation angle in radians:

• Conversion formula:$angledegree=arcdegreenumber\ast 180/\pi$
• Unity code: degree = x * Mathf.Rad2Deg;

Trigonometric functions

In a right triangle (the following figure is an example), if$a,b,c,x$The intermediate two changes can be calculated by knowing the two changes.

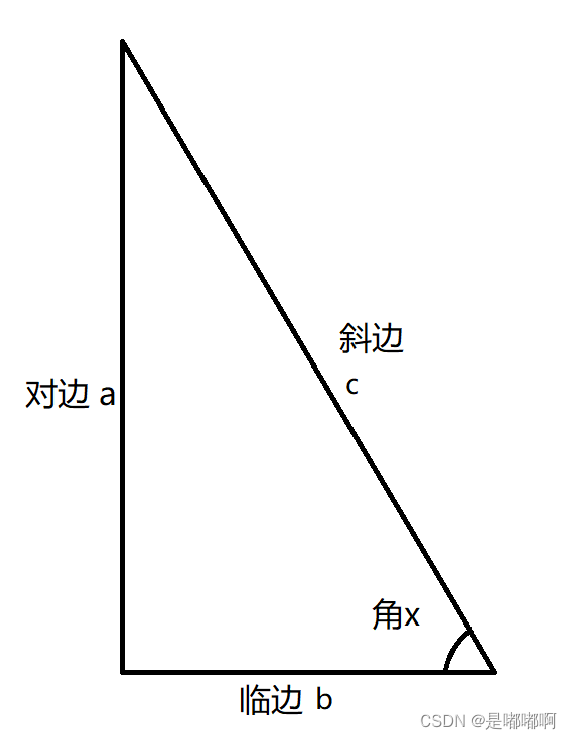
Calculation formula

正弦：$sin(x)=a/c$ （对比斜）
余弦：$cos(x)=b/c$ （临比斜）
正切：$tan(x)=a/b$ (对平临)
Extra cut ：$cot(x)=b/a$
正割：$sec(x)=c/b$
余割：$csc(x)=c/a$
反正弦：$arcsin(a/c)=x$
反余弦：$arccos(b/c)=x$
反正切：$arctan(a/b)=x$

Given one angle and one side, find the other two sides using sin, cos, and tan.
Given both sides, to find the angle, use arcsin, arccos, and arctan.

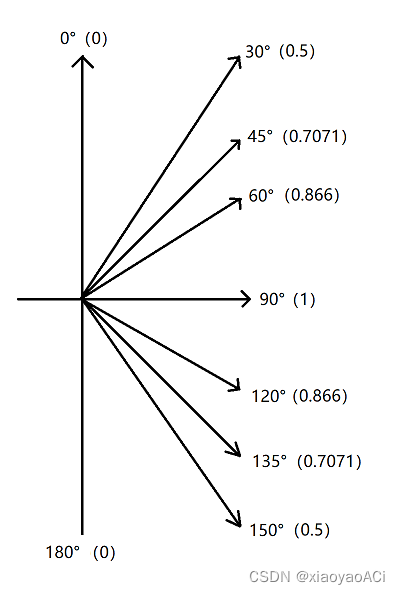
Common trigonometric function values

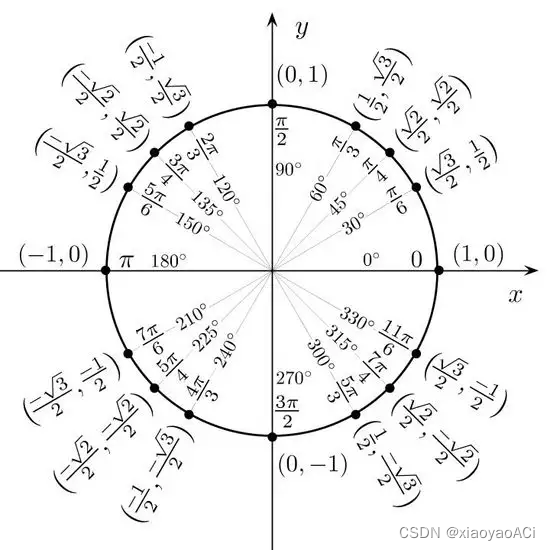
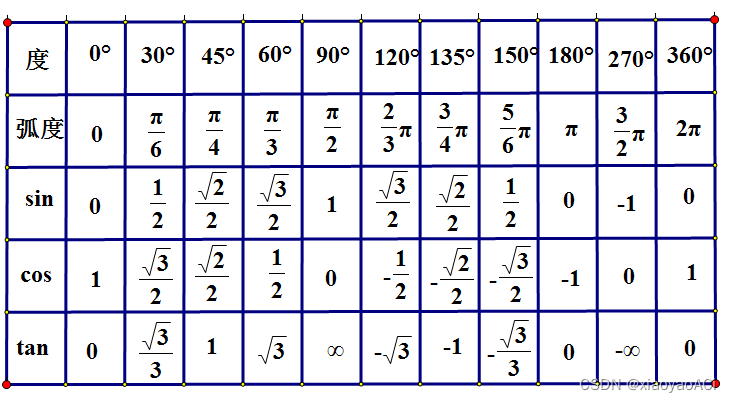
Instructions

Given an angle and a side, use $sin、cos、tan$ 。
已知两条边求角度，用 $ArcSin、ArcCos、ArcTan$ 。

Unity application

When calling trigonometric function methods such as Mathf.Sin in the code, the parameters passed in are not angles, but radians.

For example, if we want to get the value of sin30 degrees, we cannot write like this: Mathf.Sin(30). This is wrong.
The correct writing method should be Mathf.Sin(30 * Mathf.Deg2Rad). Convert the angle to radians and then pass the parameters. The result will be 0.5.

The picture below is a description of the official API.

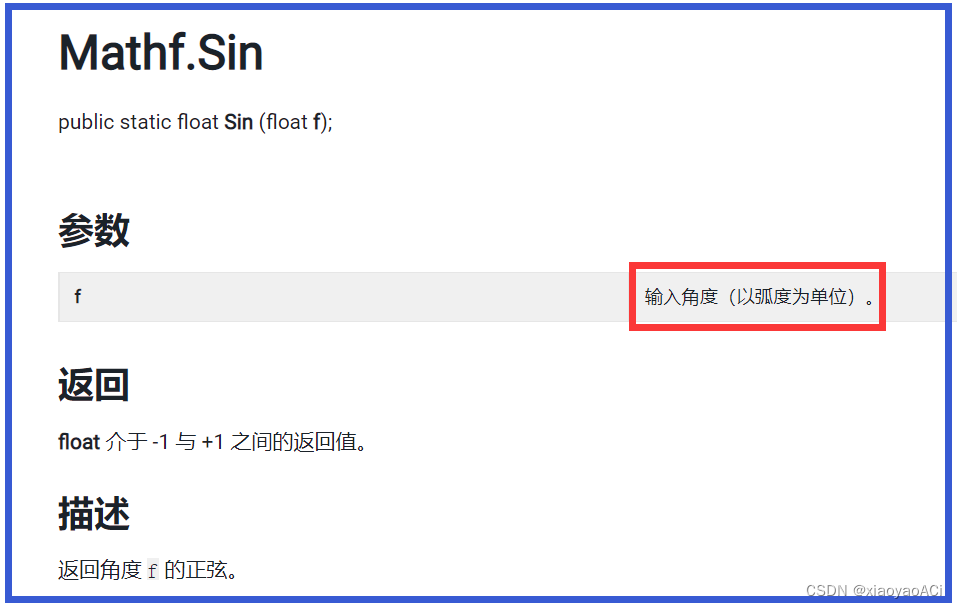
The angle required to be input is in radians, so conversion between angles and radians is often required when using these methods.

vector

A vector is a list of numbers that represents a directional displacement in each dimension. It is a physical quantity with magnitude and direction. The magnitude is the modulus length of the direction, which describes the direction of the vector in space. Vectors can be used to represent the position and orientation of objects.

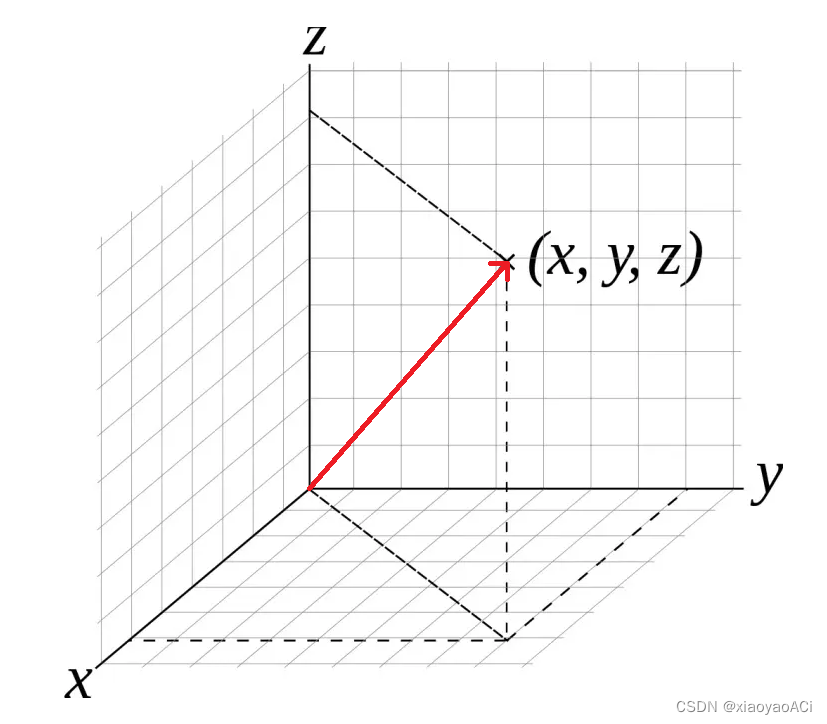
The size of the vector: that is, the length of the vector (generally called the module). The module of the vector a is $|\vec{a}|$ ，若 $\vec{a}=(x,y,z)$ 则 $|\vec{a}|=\sqrt{x^2+{and}^2+{With}^2}$ . The code usesmyVector.magnitude to get the size of the vector.

Unit vector: A vector with modulus 1. In Unity, the unit vector also represents the direction of the vector. It can be written as $\hat{a}$ . The unit vector of a vector can be obtained by dividing its modulus, that is, $\hat{a}=\frac{\vec{a}}{|\vec{a}|}$ . The code usesmyVector.normalized to obtain the unit vector of the vector, which is the direction of the vector.

Zero vector: A vector with modulus 0. The direction of the zero vector is arbitrary.

Opposite vector: A vector with equal length and opposite direction, $\vec{a}$The opposite vector of is $-\vec{a}$。

Parallel (collinear) vector: non-zero vector with the same or opposite direction, denoted as $\vec{a}//\vec{b}$。

Vector addition and subtraction

The addition and subtraction of vectors is the addition and subtraction of the corresponding components of the vector, similar to the orthogonal decomposition of forces in physics.

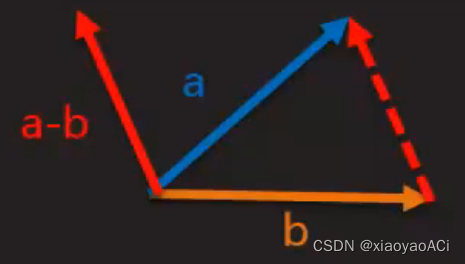
vector subtraction

Subtracting vectors equals subtracting their components.

$[x1,y1,z1]-[x2,y2,z2]=[x1-x2,y1-y2,z1-z2]$

Geometric meaning: Subtract vector a from vector b, and the result is understood as a vector starting from the end point of b and ending with the end point of a. The direction is from b to a.
Note: We can understand vector subtraction as the connection of the end points of a and b, but in fact the exact starting position of the vector should be the origin of the coordinates.

Practical application: Calculate the distance and relative direction between two points.

vector addition

Adding vectors equals adding their components.

$[x1,y1,z1]+[x2,y2,z2]=[x1+x2,y1+y2,z1+z2]$

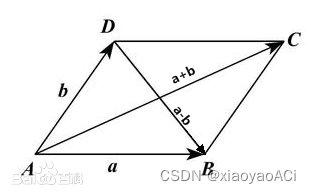
Geometric meaning: As shown below, assume that there are two vectors a and b in the space, a is parallel to a’ and has the same length, and b is parallel to b’ and has the same length. a+b is equivalent to the diagonal of the parallelogram enclosed by a, b, a’, b’.

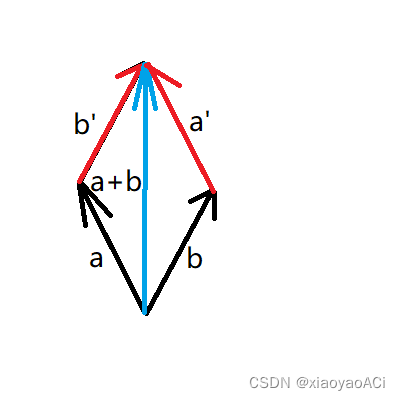
It can also be said that starting from the starting point of vector a, walk the length of a along the direction of a, and then walk the length of b along the direction of b. The point reached is equivalent to starting from a. The starting point is the length of a+b along the direction of a+b.

Practical application: Movement of objects.

Multiplication and division of vectors and scalars

Multiplication: Multiply each component of the vector with a scalar$k[x,y,z]=[xk,yk,zk]$.
Division: Dividing each quantity in terms of direction $[x,y,z]/k=[x/k,y/k,z/k]$ .
Geometric meaning: scale vector length.

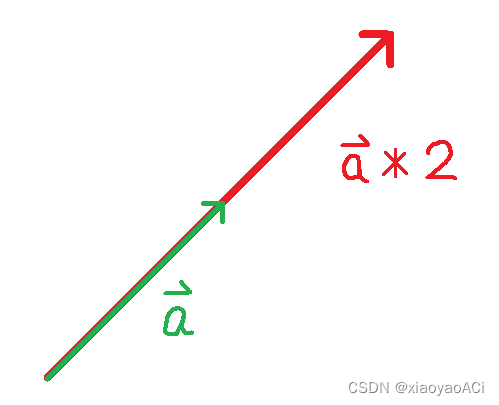
Practical applications: acceleration, deceleration, zooming in, zooming out.

Click and multiply

Dot product is also calleddot product or inner product . Expressed as the sum of the products of each component.

$[x1,y1,z1]\cdot [x2,y2,z2]=x1x2+y1y2+z1z2$

Note that the result is not a vector, but a scalar, which can be negative.

What does it mean:$a\cdot b=|a||b|\cos (a,b)$ When the modulus of a and b is 1, the dot product value of ab is the cos value of ∠ab, and then through the inverse The angle is obtained by cosine.

// 计算点乘值
float dot = Vector3.Dot(a.position.normalized, b.position.normalized);
// 计算夹角
float angle = Mathf.Acos(dot) * Mathf.Rad2Deg;

The first step is to calculate the point product value, and the second step is to calculate the angle.

Practical application: Calculate the angle between two vectors.

Common results of dot multiplication: For normalized vectors, if the directions are the same, the dot multiplication is 1; if the directions are opposite, the dot multiplication is -1; if the vectors are perpendicular to each other, the dot multiplication is 0.

Summary: Dot product can be used to calculate vector angles, but it can only be used to calculate internal angles, that is, angles less than 180°. If you want to exceed 180°, you need to combine it with cross product. The result of dot multiplication is a single numerical value.

cross

Cross product is also called "cross product" or "outer product". It is different from the result of dot product. The result of cross product is a vector, a vector perpendicular to the plane composed of two vectors. The module length is the product of the module lengths of the two vectors multiplied by the sine of the angle between them.

公式：$[x1,y1,z1]\times [x2,y2,z2]=[y1\ast z1-z1\ast y2,z1\ast x2-x1\ast z2,x1\ast y2-y1\ast x2]$

Code: Vector3 cross = Vector3.Cross(a.position, b.position);
Note: There is no need to add normalized to the cross product, and it will not affect the result whether it is added or not.

application:

1. Create a vector perpendicular to the plane;
2. Determine the relative position of two vectors.

cross product to obtain vertical vector

1. When a to b goes clockwise, then a x b points upward.
   

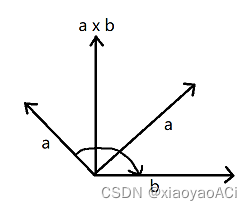
2. When a to b is counterclockwise, then a x b is facing downward.
   
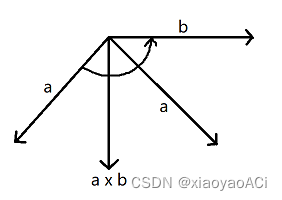
   It can also be understood this way: when the clockwise angle between a and b is less than 180, a x b faces upward; when the clockwise angle between a and b is greater than 180, a x b faces downward.

Code judgment: if the cross product result y > 0 , then it is pointing upward, it is less than 180°; if the cross product result y < 0 , then it is facing downward, it is greater than 180°;

left hand rule

The vertical vector obtained by the cross product of vectors a and b follows the left-hand rule, as shown in the figure below:

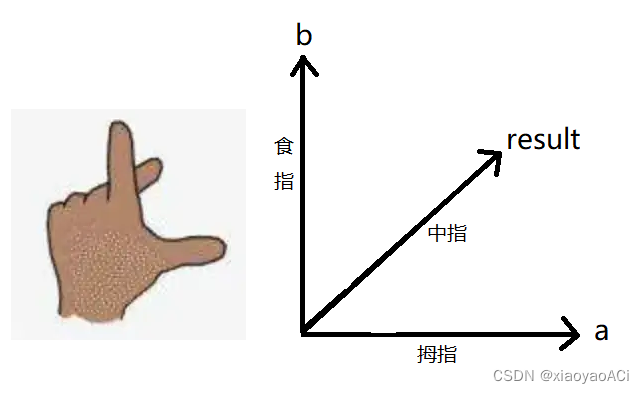
Taking the gesture above as a standard, it is perpendicular to the plane formed by thumb a and index finger b. The vector result is the result of the cross product of a and b.

Cross product calculation angle

Cross product can also be used to calculate angles, but it can only calculate 0° ~ 90°.

// 计算叉乘结果，叉乘不需要加normalized，但加了也不会有影响
Vector3 cross = Vector3.Cross(a.position, b.position);

// 用叉乘结果换算角度
float angle = Mathf.Asin(cross.magnitude) * Mathf.Rad2Deg;

Common results of cross multiplication:

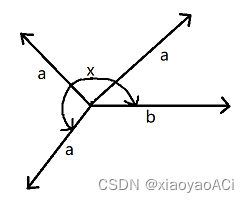
Calculate angles within 360° (dot product combined with cross product)

Point product combined with cross product can calculate angles within 360°.

// 先用点乘计算角度（180°以内）
float dot = Vector3.Dot(a.position.normalized, b.position.normalized);
float angleX = Mathf.Acos(dot) * Mathf.Rad2Deg;
// 再用叉乘后的y值确定方向
Vector3 cross = Vector3.Cross(a.position, b.position);
if (cross.y < 0)
{
    
    
	angleX = 360 - angleX;
}

First use the dot product to calculate the angle (within 180°), and then use the y value after the cross product to determine the direction. The resulting angleX is the angle from a to b clockwise.

Vector3

The Vector3 class is usually used to represent vectors in Unity. For how to use this class, please refer to my other article:[Unity] Common classes in Unity: vector Vector3, quaternion Number Quaternion

---

For more information, please view the general catalog[Unity] Unity study notes catalog arrangement