Article directory
introduction
Two reasons made me want to write this article. One is that when I was doing matrix problems, I found that these three things are often tied together, which makes people want to explore the mystery; the other is that I learned the rank of vector groups today, which made me want to A question left over from before is raised: is there a situation where the difference between the rank of the coefficient matrix and the rank of the augmented matrix is greater than 1? Maybe this question is a bit abstract, but you should be able to understand it after reading the specific instructions below.
1. Review
The cause of the problem is this. In my article on determinants, I said that the application of Cramer's law is as follows:

Some readers suggested not to write r ( A ) + 1 = r ( A ‾ ) r(A) +1 = r(\overline{A}) when the system of equations has no solutionr(A)+1=r(A) instead ofr ( A ) ≠ r ( A ‾ ) r(A) \ne r(\overline{A})r(A)=r(A) . I hadn't reviewed the equations and vectors at that time, so I had this question: Why must the difference be 1, if IAAA has many rows of 0, so can the rank of the augmented matrix be greater than 1 than the coefficient matrix?
At that time, I vaguely felt that it was a problem of ambiguity between row rank and column rank. On the one hand, in matrices, we often use elementary row transformations, ignoring column transformations and column ranks. On the other hand, column ranks are the same as row ranks in square matrices.
At first, I also thought that column rank was useless until I learned the part of vector. Since the vector we refer to is generally a column vector, then the matrix composed of a vector group naturally considers the column rank.
Therefore we aim at a general m × nm \times nm×n matrix andnnn mm_The m -dimensional vector group is sorted out, please see below.
Two, combing
For a general system of homogeneous linear equations:
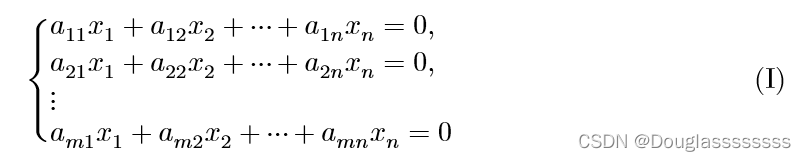
and a general system of inhomogeneous linear equations:
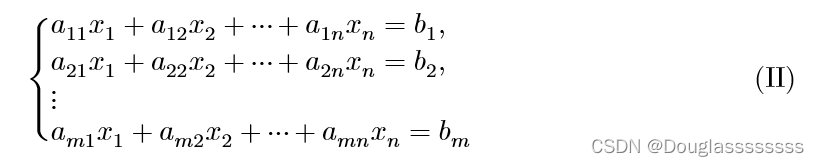
令 α 1 = ( a 11 , a 21 , … , a m 1 ) T , α 2 = ( a 12 , a 22 , … , a m 2 ) T , … , α n = ( a 1 n , a 2 n , … , a m n ) T , b = ( b 1 , b 2 , … , b m ) T \pmb{\alpha_1}=(a_{11},a_{21},\dots,a_{m1})^T,\pmb{\alpha_2}=(a_{12},a_{22},\dots,a_{m2})^T,\dots,\pmb{\alpha_n}=(a_{1n},a_{2n},\dots,a_{mn})^T,\pmb{b}=(b_{1},b_{2},\dots,b_{m})^T a1=(a11,a21,…,am 1)T,a2=(a12,a22,…,am 2)T,…,an=(a1n,a2 n,…,amn)T,b=(b1,b2,…,bm)T , then the equations (I) (II) can be expressed as the following vector form:x 1 α 1 + x 2 α 2 + ⋯ + xn α n = 0 ( 1.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\ alpha_n=0 (1.1)x1a1+x2a2+⋯+xnan=0 (1.1 ) x 1 α 1 + x 2 α 2 + ⋯ + xn α n = b ( 2.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (2.1)x1a1+x2a2+⋯+xnan=b(2.1)
令 X = ( x 1 , x 2 , … , x n ) T X=(x_1,x_2,\dots,x_n)^T X=(x1,x2,…,xn)T,matrixA= [ α 1 , α 2 , … , α n ] A=[\alpha_1,\alpha_2,\dots,\alpha_n]A=[ a1,a2,…,an] , then

the equations (I) (II) can be expressed in the following matrix form: AX = 0 (1.2) AX=0 (1.2)AX=0(1.2) A X = b ( 2.2 ) AX=b(2.2) AX=b(2.2)
homogeneous system of linear equations
For a system of homogeneous linear equations (I), it has mmm constraint equations,nnn unknowns. First of all, we should understand that no matter how many equations and unknowns there are, it is impossible to have no solutions, and there are zero solutions. What we want to discuss is to discuss whether there is a non-zero solution. We have three cases:
(一) m < n . m < n. m<n.
The number is greater than the number of dimensions, the vector group α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anmust be linearly related, then the rank of the vector group < n < n<n , according to the three-rank equality property,r ( A ) < n . r(A)<n.r(A)<n.
At this time, the number of constraint conditions of the homogeneous linear equation system is less than the unknown, and there must be an unknown that cannot be restricted. If the unrestricted unknown is non-zero, there will be a non-zero solution, that is, linear correlation.
In fact, there is nothing to discuss in this situation, because there must be a non-zero solution, so this is why it is rarely mentioned in the book.
(2) m = n . m=n.m=n.
At this point, it is necessary to discuss, because the equation system may have only zero solutions, and may also have non-zero solutions.
If the homogeneous equation system has only zero solution ⇔ \Leftrightarrow⇔Vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinearly independent ⇔ \Leftrightarrow⇔ r ( A ) = n . r(A)=n. r(A)=n.
We can now get ∣ A ∣ ≠ 0 |A| \ne 0∣A∣=0 , that is, because the coefficient matrix is square and of full rank.
If the system of homogeneous equations has nonzero solutions ⇔ \Leftrightarrow⇔Vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear correlation ⇔ \Leftrightarrow⇔ r ( A ) < n . r(A)<n. r(A)<n.
Why is it less than nnWhat about n ? Because the column vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anrank less than nnn , according to the property that the three ranks are equal, the rank of the matrix is also less thannnn 。
(三) m > n . m > n. m>n.
At this time, the number of constraint equations is more, but it does not affect anything. The rank of the coefficient matrix still satisfies r ( A ) ≤ n , r(A) \leq n,r(A)≤n , then:
If the homogeneous equation system has only zero solution ⇔ \Leftrightarrow⇔Vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinearly independent ⇔ \Leftrightarrow⇔ r ( A ) = n . r(A)=n. r(A)=n.
We cannot get ∣ A ∣ ≠ 0 |A| \ne 0∣A∣=0 , that is, because the coefficient matrix is not a square matrix, there is no determinant.
If the system of homogeneous equations has nonzero solutions ⇔ \Leftrightarrow⇔Vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear correlation ⇔ \Leftrightarrow⇔ r ( A ) < n . r(A)<n. r(A)<n.
Summarizing these three situations is actually the conclusion of the second situation. Therefore, regardless of whether it is a square matrix or not, the number of unknowns and equations, there are the following conclusions: namely
- A system of homogeneous equations has only zero solutions ⇔ \Leftrightarrow⇔Vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinearly independent ⇔ \Leftrightarrow⇔ r ( A ) = n . r(A)=n. r(A)=n.
- Homogeneous equations have nonzero solutions ⇔ \Leftrightarrow⇔Vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear correlation ⇔ \Leftrightarrow⇔ r ( A ) < n . r(A)<n. r(A)<n.
Inhomogeneous system of linear equations
For the inhomogeneous system of linear equations (II), it has mmm constraint equations,nnn unknowns, the right-hand constant vector isb = ( b 1 , b 2 , … , bm ) \pmb{b=(b_1,b_2,\dots,b_m)}b=(b1,b2,…,bm) , the augmented matrix isA ‾ = [ A ∣ b ] . \overline{A}=[A|b].A=[A∣b].
We start from its corresponding homogeneous linear equation system (I), if (I) has only zero solution, according to the above conclusion, there are vector groups α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\ dots,\alpha_n}a1,a2,…,anLinearly independent and r ( A ) = n . r(A)=n.r(A)=n.
Next we discuss the non-homogeneous situation at this time. If the non-homogeneous linear equations (II) have no solution, then the vector b \pmb{b}b cannot be separated by an unrelated set of vectorsα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear representation, so the column vector set of augmented matrix α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b}a1,a2,…,an,b is also linearly independent, sor ( A ‾ ) = n + 1 r(\overline{A})=n+1r(A)=n+1. At this point we need to discussm, nm, nm,The quantitative relationship between n , by r ( A ) = nr(A)=nr(A)=n known,m ≥ nm \geq nm≥n . Ifm = nm = nm=n ,有 r ( A ‾ ) ≤ { m , n + 1 } = m = n r(\overline{A})\leq \{m,n+1\}=m=n r(A)≤{ m,n+1}=m=n ,与 r ( A ‾ ) = n + 1 r(\overline{A})=n+1 r(A)=n+1 contradictory; ifm > n m>nm>n andm = n + 1 m=n+1m=n+1,有r ( A ‾ ) ≤ { n + 1 , n + 1 } = n + 1 r(\overline{A})\leq \{n+1,n+1\}=n+1r(A)≤{ n+1,n+1}=n+1 , meet; ifm > n + 1 m>n+1m>n+1 , thenr ( A ‾ ) ≤ { m , n + 1 } = n + 1 r(\overline{A}) \leq \{m,n+1\}=n+1r(A)≤{ m,n+1}=n+1 , complies with.
Therefore, for m ≤ nm \leq nm≤The non-homogeneous linear equations of n , it is impossible to have no solution at this time; and for m ≥ n + 1 m \geq n+1m≥n+1 non-homogeneous linear equations, at this time the conclusionr ( A ‾ ) = n + 1. r(\overline{A})=n+1.r(A)=n+1.
If the nonhomogeneous system of equations (II) has a solution, then the vector b \pmb{b}b can be vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear representation, and because the vector group α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinearly independent, so r ( A ‾ ) = n = r ( A ) . r(\overline{A})=n=r(A).r(A)=n=r(A).
If the homogeneous equations (I) corresponding to the equations (II) have non-zero solutions, according to the conclusion of the previous part, the equations α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots, \alpha_n}a1,a2,…,anLinearly dependent and r ( A ) < n . r(A)<n.r(A)<n.
We discuss the situation of non-homogeneous equations (II) at this time. If the equations (II) have no solution, then the vector b \pmb{b}b cannot be divided into vector groupsα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear representation, but due to the vector set α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anis linearly related, so the column vector group of the augmented matrix α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b}a1,a2,…,an,b is linearly related, andr ( A ‾ ) < n + 1 r(\overline{A})<n+1r(A)<n+1 且 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
Because the vector b \pmb{b}b cannot be divided into vector groupsα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear representation, then the vector group α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b}a1,a2,…,an,The rank ratio vector group of b α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,an 多 1 ,即 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
OOcan be understood intuitively. The vector group is column-by-column, and a column that cannot be represented by the original column is added, so the rank must be increased by 1.
If the equation system (II) has a solution, then the vector b \pmb{b}b can be vector groupα 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n}a1,a2,…,anLinear representation, so r ( A ‾ ) = r ( A ) < n . r(\overline{A})=r(A)<n.r(A)=r(A)<n.
The characteristics of rank in all cases are discussed as shown in the figure below.

In summary, the following general conclusions can be drawn:
- Inhomogeneous equations have solutions ⇔ \Leftrightarrow⇔ r ( A ‾ ) = r ( A ) . r(\overline{A})=r(A). r(A)=r(A).
- Inhomogeneous equations have no solution ⇔ \Leftrightarrow⇔ r ( A ‾ ) ≠ r ( A ) , r(\overline{A})\ne r(A), r(A)=r(A), 或 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
In fact, if there is a solution, we can discuss it again, so let's put it in the chapter of equations later and let's talk about it in detail.
write at the end
It seems that I have neglected the nature of the equality of three ranks, so that the question at the beginning arises.
Now it is increasingly recognized that vectors are an important tool throughout linear algebra.