Table of contents
2 Conditional expectation, full expectation formula
3.2 Differences and connections
3.3 Probability and Stochastic Processes
4 What is the use: ---It can solve many recursive problems
4.1.1 Are you looking for the number of times or the quantity?
4.1.2 Determine the target variable you require
4.3 Example 2: Find the number and calculate the expectation of the geometric distribution
5 The difference between conditional expectation total expectation formula and Markov transition
1 Objective Question: What are conditional expectations? What is the use of conditional expectations?
Let's not talk about the goal this time, let's start with a primary school math problem
Q: Assuming that the average score of class 1 is 93, and the average score of class 2 is 95, how to calculate the average score of the two classes?
Wrong algorithm: (93+95)/2=94
- It is false unless the two classes have the same number of students
- This can't use simple arithmetic average, you have to use weighted average
correct algorithm
- Suppose the number of students in class 1 is n1, the average score A1=93, and the number of students in class 2 is n2, the average score A2=95
- According to the definition of average
- A0 = total score/total number of people
- = (A1*n1 + A2*n2)/(n1+n2)
- = n1/(n1+n2)*A1 + n2/(n1+n2)*A2
- = Coefficient 1*A1+ Coefficient 2*A2
- = Number of people weight ratio 1*A1+ Number of people weight ratio 2*A2
- And the weight = the number of people in this class / sum (the sum of the number of people in all classes)
A question arises from here
Q1: We want to know the overall average, of course we can directly use the overall number to calculate, such as A0 = total score/total number of people. But if we already know the average value of each part of the population, can we calculate the average value of the population based on these?
A1: The answer is yes, as seen in the previous example, the overall mean = Σ partial mean * weight ratio.
Q2: Then ask, if the population is not deterministic, but a random variable, for example, what we ask is: what is the expectation of this random variable?
A2: Then the weight ratio becomes the probability of random variables. In fact, this is the content of conditional expectation and full expectation formula
So that leads us to the topics we want to discuss:
- Analogy: overall mean = Σpartial mean * weight ratio
- I hope it looks like this
- E(X) = ΣPi*E(X|Yi) is the same expression as above
- E(X) =E(E(X|Y))
- E(X) = P1*E(X|Y1) + ..... +Pk*E(X|Yk) = ΣPi*E(X|Yi)
- E(X) = E(E(X|Y)) = ΣPI*E(X|Yi) = P1*E(X|Y1) + ..... +Pk*E(X|Yk) ,where i belonging to (1,k)
2 Conditional expectation, full expectation formula
The concepts of the following different ways of writing are different
- step1: E(X) is a specific number, the mathematical expectation of the random variable = the (probability) weighted average of the random variable = the specific number
- step2: Because under the premise of Y=y1, X may still have several situations, assuming it is also x1, x2...xk, so the conditional expectation is E(X|Y=y1) = Σxi*P(xi|Y=y1 ) = x1*P(x1|Y=y1) +x2*P(x2|Y=y1) +...+xk*P(xk|Y=y1)
- step3: For random variables X and Y, there are multiple values y1, y2....yj, such as E(X|Y=y1) itself also corresponds to a probability Pj. Therefore, the expectation E(E(X |Y)) =ΣPI*E(X|Yj) = P1*E(X|Y1) + P2*E(X|Y2) +.....+Pj*E(X|Yj) Prove that E(E(X|Y))=E(X)
- step4: So the full expectation formula E(X) = E(E(X|Y)) = ΣPI*E(X|Yi) = P1*E(X|Y1) + P2*E(X|Y2) + .. ... +Pj*E(X|Yj) , where i belongs to (1,j)
See the picture below to understand
The picture is from Zhihu, refer to zhuanlan.zhihu.com/p/612709393
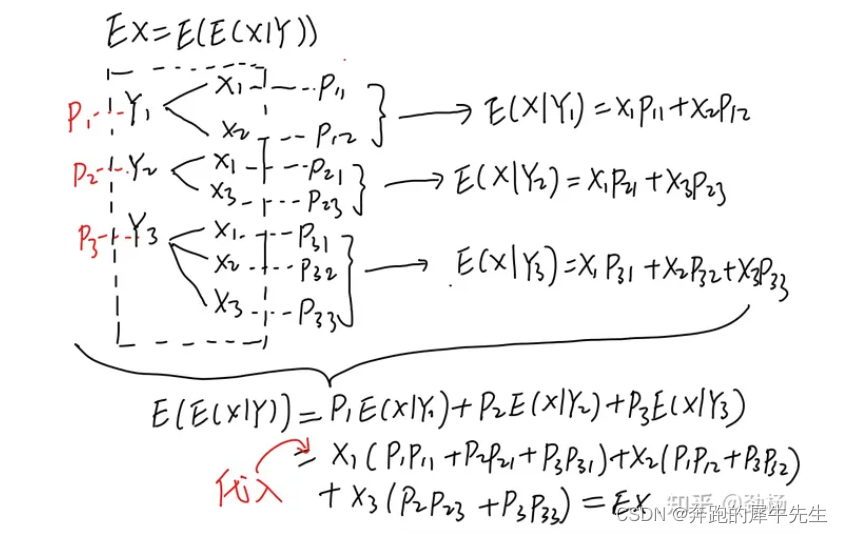
3 Conditional expectation, full expectation formula and conditional probability, the difference and connection of full probability formula
3.1 The formula is as follows
- Conditional probability: P(A|B) = P(AB) / P(B)
- Total probability formula: P(A) = P(AB1) * P(B1) +P(AB2) * P(B2) + ......+P(ABn) * P(Bn)
- Conditional expectation: E(X|Y=y1) =E(X|y1) = Σxi*P(xi|Y=y1)
- Full expectation formula: E(X) = E(E(X|Y)) = ΣPj*E(X|Yj) = P1*E(X|Y1) + ..... +Pj*E(X|Yj ) , where j belongs to (1,k)
3.2 Differences and connections
- Conditional probability, the total probability formula, is used to calculate the probability
- Conditional expectation, the full expectation formula, is used to find the expected value of various random variables, not the probability, for example, the average number of times of synthesis, the average number of targets of synthesis... and so on.
3.3 Probability and Stochastic Processes
- Probability is generally to find the possibility of instantaneous/tangential occurrence, mainly focusing on probability
- Stochastic processes generally seek the situation within a time course, or the situation after a time course, and can focus on probability, frequency, and quantity. . . etc.
4 What is the use: --- It can solve many recursive problems
4.1 There is a premise before use: clearly define the target and type of the random variable you require
4.1.1 Are you looking for the number of times or the quantity?
The reason why conditional expectation and total expectation formulas are not as easy to understand as conditional probability and total probability formulas is because they need to be carefully understood. Among the problems to be analyzed, what is the target-random variable?
- Do you want to know the number of random variables after multiple randoms?
- Do you want to know the number of times it takes to reach a certain state after multiple randoms? somewhat geometric distribution
- etc.
4.1.2 Determine the target variable you require
- For example, the probability that an A may become A, B, C, and D is 0.5, 0.2, 0.2, 0.1
- So if we have 100 A, how many D can be generated?
- So if we have 100 A, how many C can be generated?
- If I want to synthesize 1 D, how many times do I need to do it?
- these are all different questions
4.2 Example 1: Calculated time = number of steps = number of times, which belongs to this type of problem
- A miner is trapped in a mine, and there are 3 doors that can be opened in front of him. With equal probability, it takes 3 hours to return to the outside with 1 door, 5 hours to return to the current location with 1 door, and 7 hours to return to the current location with 1 door. Ask the average time it takes miners to return to the outside?
- Set X to be the time it takes miners to go out
- E(X) = 1/3* 3+ 1/3* (E(X)+5)+1/3* (E(X)+7)
- 3 E(X) = 3+ E(X)+5 +E(X)+7
- E(X) = 15
4.3 Example 2: Find the number and calculate the expectation of the geometric distribution
if you toss a coin
Assuming that the success probability of heads is p, and the failure probability of tails is 1-p, what is the number of times until one success? (same geometric distribution)
It can be directly calculated by the probability and expectation formula of the geometric distribution
- Geometric distribution probability: pdf=p*(1-p)^n
- Expected order of geometric distribution: E(X)=1/p
Conditional expectation and full expectation formulas can also be used
Let n be the number of heads in the 1st run, and Y denote the heads and tails of a single experiment
E(N) =P*E(N|Y=1) + (1-P)*E(N|Y=0)
- Obviously E(N|Y=1) =1, because since Y=1, it is successful, and the number of times N is also =1
- And because Y=0, it has been one more time, and each test is independent and starts to retest E(N), so E(N|Y=0) =1+E(N)
This is the law of recursion
- E(N) =P*1 + (1-P)*(1+E(N))
- E(N) =P +(1-P)+ (1-P)*E(N)
- E(N) =1+ (1-P)*E(N)
- E(N) =1/p
This is also a recursive problem
4.4 Example 3: Find the number, fit the binomial distribution to find the expectation of the number of successes
Q: If you flip a coin
Assuming that the probability of success of heads is p, and the probability of failure of tails is 1-p, how many times are the average successes until 100 throws? (how many heads?)
A: As long as p is not equal to 0, and because each toss of a coin is independent, theoretically it may be heads/tails each time, so 100 trials, the number of heads may be (0, 100)
So how many heads will appear on average?
- Not suitable for geometric distribution to find the number of times of the last success
- The quadratic distribution seems to be appropriate. The probability of the binomial distribution is the probability of success K times, and the expectation of the binomial distribution is np, which is the sum of the corresponding probabilities for all different values of k, E(X) =np is exactly the average number of successful k times.
- Conditional expectation and full expectation formulas can also be used
And Y represents the pros and cons of a single experiment
The number of possible heads in a trial
E(N) =P*E(N|Y=1) + (1-P)*E(N|Y=0)
E(N) =P*1 + (1-P)*0
- If E(N|Y=1), because since Y=1, it is successful, then there will be 1 positive number 1
- If E(N|Y=0), it means that the negative side is generated this time, and the front side is not generated, so the number of front sides is 0
This is the law of recursion
- First look at the single test
- E(N) =P*1 + (1-P)*0
- E(N) =P
- while the N trials are independent
- so
- n*E(N)=np
5 The difference between conditional expectation total expectation formula and Markov transition
Summary 1:
- Generally speaking, you can use conditional expectations and so on to find the number of times and the number of counts.
- The Markov chain is generally used to calculate the probability, of course, it can also be used to calculate the average number of times
Summary 2:
- Conditional expectation, the full expectation formula, is more applicable than the Markov chain,
- The requirements of Markov chain are stricter, but it is faster and more convenient to handle the situation that is suitable for processing.
- Markov chains only focus on the relationship between n-1 states and n states
- Markov chains are generally suitable for one thing to switch between multiple states, and are generally not suitable for synthetic problems such as variable 1
- It is generally required that the weights of each state are equal, the step size is equal, and it cannot be distorted. And if the number of states is too large, it seems that the Markov chain calculation is also very troublesome.