2022 Tianfu Cup National Undergraduate Mathematical Contest in Modeling
Question B The first "jun" love
Reproduction of the original title:
Recently, the conflict between Russia and Ukraine has intensified. It is not difficult to find that modern warfare is still a human-dominated war, and has not entered a state of fully mechanized warfare. Then the supply of military materials in war is very important. The ancient Chinese art of war said that "before the soldiers and horses move, the food and grass go first" is the embodiment of this point. In modern warfare, soldiers often do not bring a large amount of food and ammunition at one time. If they are caught in a more protracted combat state, they need to mobilize the logistics troops in the supply station to quickly replenish supplies.
Near a supply station in a certain place, there are 4 troops that need to replenish supplies at the same time, and there are two types of aircraft, A and B, in the supply station. There are 6 aircraft in category A, with a maximum load of 13 tons and a flight speed of 260km/h; There are 10 planes, with a maximum load of 20 tons and a flight speed of 50km/h. The planes can go to the troops in a straight line to drop supplies, and they can only go to one destination at a time to drop supplies. After the delivery, they need to return to the supply station and then go to the next troop to drop. supplies.
Each unit can accept more supplies than needed, but cannot accept more than 150% of the required quantity. It also takes time to load and unload the aircraft. The loading and unloading of Class A aircraft takes 20 minutes; the loading and unloading of Class B aircraft takes 30 minutes and 40 minutes for unloading.
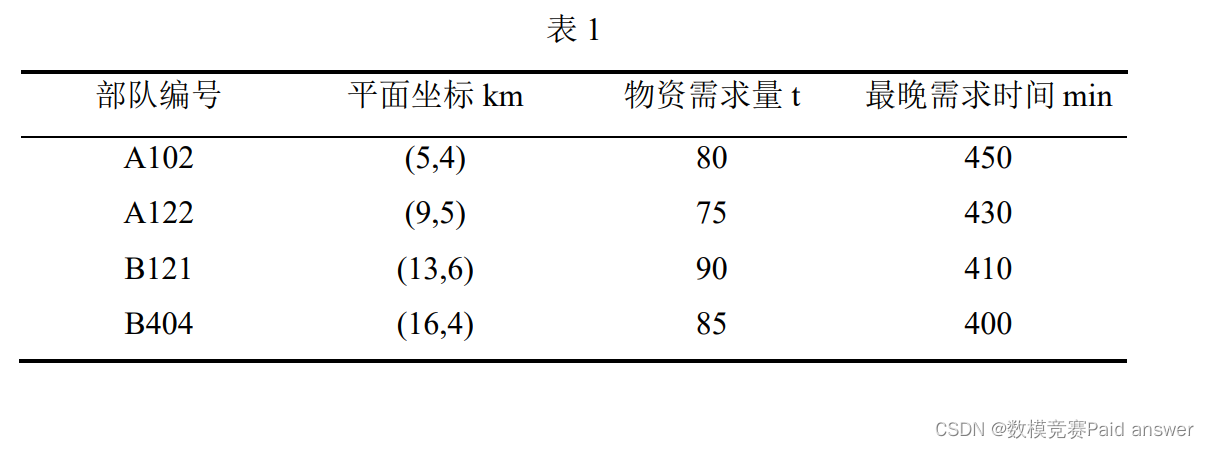
Due to the urgent military situation, the delivery time of all supplies shall not exceed the latest demand time of the unit. See Table 1 for the coordinates of the four troops, the quantity of requested materials and the latest demand time. Now the supply station invites you to be the decision maker of aircraft dispatch, please solve the following problems:
(1) Suppose the old supply station is bombed by the enemy, and a new supply station needs to be built urgently. Without considering other factors, only considering the maximum support for each unit, please establish a suitable mathematical model to determine the location of the new supply station.
(2) Due to various reasons, the new supply station is built at the coordinate (10,30), please establish a mathematical model to determine the deployment plan of the aircraft.
(3) After receiving the request from the superior, each unit needs to continue to move to the next location to perform the mission after receiving the supplies. Therefore, it cannot carry more than 110% of the required amount of supplies, and because there will be 5%-10% of the class A aircraft during the handling process. % attrition, Class B aircraft have 3%-7% attrition. Please establish a mathematical model to determine the transshipment plan.
Overview of the overall solution process (abstract)
The supply of military materials is a very important task in war. When a war falls into a protracted battle, it is necessary to mobilize the logistics troops in the supply station to quickly replenish materials. Therefore, it is very meaningful to study the problem of war material scheduling.
For problem 1, firstly, the requirements of the topic are transformed into corresponding mathematical problems, and the shortest total distance from the newly-built supply station to each army represents the maximum support for each army. From this, an unconstrained optimization model can be established, and the independent variable is the newly-built supply station location coordinates. In this paper, two methods are used to solve the unconstrained problem, namely the gradient descent method and the whale optimization algorithm. The results of the two algorithms are (10.49, 5.05) and (9.0055, 4.9992) respectively. By comparison, it is found that the optimal position solved by the whale optimization algorithm is exactly A122. Therefore, considering the war factor, the supply station is set at (10.49, 5.05 ) best, the total distance to the four units is 15.3737km.
For problem 2, firstly, transform the determined aircraft call plan required by the topic into minimizing the time to complete all transportation tasks, and use this as the objective function, the latest demand time, the aircraft exceeding the material quantity requirement, and the total number of aircraft are established as constraints The single-objective integer programming model specifies the scheduling scheme with 6 aircraft A and 10 aircraft B as independent variables. Considering that the intelligent optimization algorithm has too high requirements for generating new solutions in this question, this question uses a greedy algorithm to solve Model 2. Combining the attributes of the two types of aircraft, the greedy method is to select the unit farthest from the supply station and give priority to class B aircraft for each dispatch. The result of the solution is to dispatch 4 B aircraft to the unit A102, 5 A aircraft and 1 B planes go to unit A121, 7 A planes go to unit B121 and 5 planes go to unit B404, the transit time to complete all tasks is 102.01 minutes. Finally, the greedy method of the greedy algorithm is changed to test the model. The results show that the changed greedy algorithm cannot change the shortest time, but it will affect the amount of extra materials, which proves that the second model is reliable.
For problem 3, firstly, based on the model of problem 2, introduce the minimization of excess materials as the second objective function, adjust the quantity of materials exceeding the constraints, and consider the loss factors in the process of aircraft transportation, introduce the concept of loss factor, The uncertain loss factor is specified as the expected value within the range, and a multi-objective integer programming model is established. Model 3 is a multi-objective optimization problem, so the greedy algorithm has great limitations in Model 3. In this paper, simulated annealing algorithm is used to solve problem 3, and the minimum time to complete the transportation task is transformed into a constraint condition, and the generation of a new solution is considered to be fixed. In the solution space of the problem, the optimal solution found by the algorithm after 150 iterations is: dispatch 2 A planes and 3 B planes to troop A102, 4 B planes to troop A122, 6 A planes and 1 B plane Aircraft go to unit B121, 4 A planes and 2 B planes go to unit B404. In addition, the total amount of materials solved by simulated annealing is 334.3 tons, which is 10.79% higher than the result of the greedy algorithm of 370.375 tons, and the shortest time can still reach 102.01 minutes. Finally, the sensitivity test of the parameter loss factor is carried out by adjusting the value of the loss factor. The results show that when the degree of material loss fluctuates within a small range of the expected value, the results of the model solution will not be very different, but when the degree of loss is too large When it is large, the scheduling plan of the aircraft will change greatly, and the shortest time to complete all transportation tasks will increase by 46.98%.
Model assumptions:
1. Assume that the planes are fully loaded and depart during the transportation process, and there is no situation where a plane departs without being full; 2.
Assume that all planes can take off and depart at the same time, and support parallelism;
3. Question 3 The location of the supply station is the location of the supply station in the second question;
4. There will be no delay during the flight, and the default is to fly at a given speed;
problem analysis:
This question requires us, as the decision maker of aircraft scheduling, to solve optimization problems in three different situations. To solve this kind of pure optimization problems, the problem-solving ideas are mainly divided into two steps: the first step is to clarify the objective function of the topic, and find the constraints required by the topic; the second step is to use the optimization method to solve the model; for the unconstrained optimization problem of the problem, It can be solved with the help of gradient method, or it can be solved with intelligent optimization algorithm. For the constrained integer programming problem of problem 2, the simplest solution is to specify the greedy rule and use the greedy algorithm to solve it. For problem three, it is necessary to consider the change of constraint conditions and the selection of dual objectives. This paper uses simulated annealing algorithm to solve it.
Analysis of Question 1
In question 1, it is assumed that the old supply station was blown up by the enemy, and a new supply station needs to be urgently built. Regardless of other factors, only consider the ability to provide support to each unit to the greatest extent. The idea of this question is divided into two steps: 1. Determine the
meaning of providing support to each unit to the greatest extent as required by the question, and transform the station building problem into a mathematical problem. . Analyzing the data in the attached table, we found that the maximum support for each unit can be understood as the minimum total distance from the new station to the four units, so we can establish an unconstrained optimization model; 2. Solve the unconstrained
method Various, the most mainstream methods are gradient-based methods, such as gradient descent method, Newton method and quasi-Newton method, etc., non-gradient-based methods such as evolutionary algorithm and swarm intelligence algorithm, etc. Common ones include simulated annealing, Genetic algorithm and particle swarm algorithm, etc., this paper chooses a swarm intelligence optimization algorithm with a stronger solution ability than conventional algorithms—whale algorithm. The results of the two algorithms are compared and analyzed, and the station building schemes in different realistic situations are given.
Analysis of Question 2
In question 2, due to various reasons, the new supply station is built at the coordinates (10, 30), let us establish a mathematical model to determine the deployment plan of the aircraft. After knowing the coordinates of the new supply station, we can use the given coordinates to schedule the aircraft to deliver supplies. As for how to schedule the aircraft, the second question needs to be determined. Similar to the first question, we must first find a suitable objective function and constraints, so as to transform the aircraft scheduling problem into a planning problem. This article needs to consider a variety of factors, such as the delivery time of all materials must not exceed the latest demand time of the unit, the maximum load of all aircraft, and so on. Obviously, this is an integer programming model, and the independent variable is the scheduling situation of 16 aircrafts. The objective function title is not clearly given, but the objective function is determined to minimize the transportation time in consideration of the actual situation. There are many ways to solve integer programming, such as simulated annealing, greedy algorithm, etc. How to choose the optimal solution needs to consider the constraints given by the title. In this paper, the greedy algorithm is used to solve the planning model. Compared with the simulated annealing algorithm , the greedy algorithm is simpler, and the greedy algorithm does not need to generate solutions in the solution space every time like simulated annealing. The greedy algorithm is iterative step by step, and each step is optimal, and the final total result is the optimal. Finally, we test and analyze the results of the greedy algorithm, and give a more accurate improvement plan.
Analysis of Question Three
Question 3 is to add new constraints on the basis of Question 2, that is, the question clearly stipulates that each unit needs to continue to move to the next location to perform tasks after receiving supplies, so the amount of materials stored by each unit cannot exceed the specified 110% of the required quantity. And in the third question, the loss of the handling process is newly added, and the loss of the A-type aircraft is different from that of the B-type aircraft, which causes a certain degree of randomness to the results of the model solution. For such random problems , we generally have two solutions. The first is to convert random factors into fixed factors, thereby reducing complexity, but the result of this is that the robustness of the model is not strong. Another method is to maintain randomness, and each decision needs to consider random factors. Obviously, doing so will increase the difficulty of the topic. In addition, in the third question, we consider that the optimal scheduling is not only optimal in time, but also the scheduling result needs to be optimal, so we introduce the minimization of excess materials as the second objective function, and establish a multiple Objective integer optimization model. In order to simplify the difficulty of solving, we first fixed the value of the loss factor, and converted the minimum transportation time into a constraint condition, so that the dual-objective model became a single-objective model, and the simulated annealing algorithm was used to solve the model, and finally the loss factor of the model A sensitivity analysis was performed on the parameters.
Model establishment and solution Overall paper thumbnail


For all papers, please see below "Only modeling QQ business cards" Click on the QQ business card
Part of the program code: (code and documentation not free)
1. clc
2. clear
3.
4. % 绘图函数
5. % draw
6.
7. % 求最优位置
8.
9. % 鲸鱼算法
10.% 参数初始化
11.a = 2; % 初始游动因子的值,后续会不断缩减
12.MAX_iter = 200; % 迭代次数
13.iter = 1; % 初始化迭代次数
14.b = 3; % 螺旋系数
15.number = 100; % 定义鲸鱼的数量
16.fitt = zeros(number,1); % 初始化适应度
17.x = zeros(number,2); % 初始化种群
18.l_min = ‐100; %自变量下界
19.l_max = 100; % 自变量上界
20.for i = 1:number % 初始化种群和适应度
21. x(i,1) = l_min + rand(1) * (l_max ‐ l_min);
22. x(i,2) = l_min + rand(1) * (l_max ‐ l_min);
23. fitt(i) = fit(x(i,:));
24.end
25.fit_best = min(fitt); % 记录最优适应度
26.ind = find(fitt == min(fitt),1);
27.X_best = x(ind,:); % 记录最优位置
28.X_BEST = []; % 记录全局
29.FITT = []; % 记录全局
30.%% 迭代开始
31.while iter <= MAX_iter
32. for i = 1:number
33. if rand() < 0.5 % 采用游动捕食
34. a = 2 * (1 ‐ iter / MAX_iter); % 更新游动因子
35. r = rand(1,2); % 随机数
36. C = 2 * r; % 计算摆动因子
37. A = 2 * r * a ‐ a; % 计算收敛因子
38. if sqrt(A(1)^2 + A(2)^2) < 1 % 采取包围捕食
39. D = abs(C .* X_best ‐ x(i,:)); % 计算最优距离
40. x(i,:) = X_best ‐ A .* D; % 这里是位置更新
41. if x(i,1) < l_min || x(i,1) > l_max % 判断是否超
出边界
42. x(i,1) = l_min + rand(1) * (l_max ‐ l_min);
43. end
44. if x(i,2) < l_min || x(i,2) > l_max
45. x(i,2) = l_min + rand(1) * (l_max ‐ l_min);
46. end
47. else % 采取随机游动
48. rand_ind = unidrnd(20); % 随机抽取鲸鱼
49. D = abs(C .* x(rand_ind,:) ‐ x(i,:));
50. x(i,:) = x(rand_ind,:) ‐ A .* D;
51. if x(i,1) < l_min || x(i,1) > l_max % 判断是否超
出边界
52. x(i,1) = l_min + rand(1) * (l_max ‐ l_min);
53. end
54. if x(i,2) < l_min || x(i,2) > l_max
55. x(i,2) = l_min + rand(1) * (l_max ‐ l_min);
56. end
57. end
58. else % 采用气泡捕食
59. D_1 = abs(X_best ‐ x(i,:));
60. l = unifrnd(‐1,1); % 随机数
61. x(i,:) = D_1 * exp(b * l) * cos(2 * pi * l) + X_best
;
62. if x(i,1) < l_min || x(i,1) > l_max % 判断是否超出边
界
63. x(i,1) = l_min + rand(1) * (l_max ‐ l_min);
64. end
65. if x(i,2) < l_min || x(i,2) > l_max
66. x(i,2) = l_min + rand(1) * (l_max ‐ l_min);
67. end
68. end
69. fitt(i) = fit(x(i,:)); % 每更新一次位置,求解一次适应度
70. end
71. disp(['当前迭代次数为:',num2str(iter)])
72. % 迭代完一次更新数据
73. fit_best = min(fitt); % 更新当前代数中种群的最优解
74. ind = find(fitt == min(fitt),1);
75. X_best = x(ind,:); % 更新最优位置
76. X_BEST = [X_BEST;X_best];
77. FITT = [FITT;fit_best];
78. iter = iter + 1;
79.end
80.Fit_Best = min(FITT);
81.ind_best = find(FITT == min(FITT),1);
82.X_BE = X_BEST(ind_best,:);
83.disp(['找到的最优解为:',num2str(Fit_Best)])
84.disp(['最优解对应的 X:',num2str(X_BE)])
85.figure(2)
86.plot(1:MAX_iter,FITT)
87.title('种群迭代图')
88.xlabel('迭代次数')
89.ylabel('适应度值')