Graph Theory and Search

Search and Graph Theory

Search and Graph Theory

Depth First Search DFS
Breadth First Search BFS
Tree and Graph Storage
Depth-first traversal of trees and graphs
Breadth-first traversal of trees and graphs
topological sort

Depth First Search DFS

Two important concepts in DFS: backtracking and pruning

BFS is generally related to the shortest path, DFS does not

Backtracking Note: Remember to restore the scene

template:

void dfs (int k)
{
    
    
	if (到目的地)
	{
    
    
		输出解;
		return;
	}
	for (int i = 1; i <= 算法种数; i++)
	{
    
    
		if (满足条件)
		{
    
    
			保存结果，保存现场状态;
			dfs(k + 1);
			恢复保存结果之前的状态; // 回溯一步
		}
	}
}

arrange numbers

Title: AcWing 842. Arranging Numbers - AcWing

DFS process for full permutation:

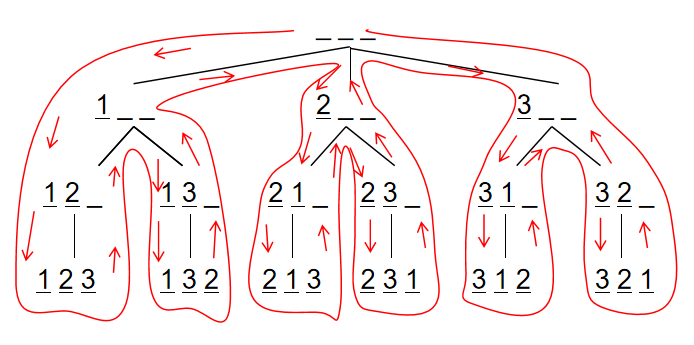
#include <iostream>
using namespace std;
const int N = 10;

int n;
int path[N]; // 路径
bool vis[N]; // 是否访问过

void dfs(int u)
{
    
    
    if (u == n)
    {
    
    
        for (int i = 0; i < n; i++) cout << path[i] << " ";
        puts("");
        return;
    }
    for (int i = 1; i <= n; i++)
    {
    
    
        if (!vis[i])
        {
    
    
            // 标记已访问，并添加到路径
            path[u] = i;
            vis[i] = true;
            // 继续搜索
            dfs(u + 1);
            // 回溯
            vis[i] = false;
        }
    }
}

int main()
{
    
    
    cin >> n;
    dfs(0); // 从 path[0] 开始
    return 0;
}

n queen

Title: AcWing 843. The n-queen problem - AcWing

Reference problem solution: AcWing 843. n-queen problem (enumerate by row or enumerate by each element) - AcWing

Solution 1: Enumerate by row

#include <iostream>
using namespace std;
const int N = 20;

int n;
char g[N][N]; // 存储路径
// bool 数组用来判断搜索的下一个位置是否可行
// col 列, dg 对角线(左上->右下), udg 反对角线(左下->右上)
bool col[N], dg[N], udg[N];

// 按行搜索
void dfs(int u)
{
    
    
    if (u == n)
    {
    
    
        for (int i = 0; i < n; i++) puts(g[i]);
        puts("");
        return;
    }
    // 枚举 u 这一行，搜索合法的列
    int x = u;
    for (int y = 0; y < n; y++) 
    {
    
    
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        if (!col[y] && !dg[y - x + n] && !udg[y + x]) 
        {
    
    
            // 标记已访问，并加入路径
            col[y] = dg[y - x + n] = udg[y + x] = true;
            g[u][y] = 'Q';
            // 向下搜索
            dfs(u + 1);
            // 回溯
            g[u][y] = '.';
            col[y] = dg[y - x + n] = udg[y + x] = false;  
        }
    }
}

int main()
{
    
    
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            g[i][j] = '.';
    dfs(0);
    return 0;
}

Solution 2: enumerate by grid

#include <iostream>
using namespace std;
const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];

// 比较原始的 dfs 搜索，每一格都搜，s 表示皇后数量
void dfs(int x, int y, int s)
{
    
    
    // 换行
    if (y == n) y = 0, x++;
    if (x == n)
    {
    
    
        // 摆好了 n 个皇后
        if (s == n)
        {
    
    
            for (int i = 0; i < n; i++) puts(g[i]);
            puts("");
        }
        return;
    }
    // 不放皇后
    dfs(x, y + 1, s);
    // 放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
    {
    
    
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1); // 递归下一层
        g[x][y] = '.';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
    }
}

int main()
{
    
    
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            g[i][j] = '.';
    dfs(0, 0, 0);
    return 0;
}

Breadth First Search BFS

BFS can be used to find the shortest path only when the weights of all edges are 1.

walk the maze

Title: 844. Maze-AcWing Question Bank

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 110;
typedef pair<int, int> PII; // 二元对
// 方向向量
int dx[4] = {
    
    -1, 0, 1, 0}, dy[4] = {
    
    0, 1, 0, -1}; 

int g[N][N], d[N][N];
int n, m; // n x m 的矩阵

void bfs()
{
    
    
	// 距离初始化为 —1
    memset(d, -1, sizeof d);
    d[0][0] = 0; // 起点初始化为 A
    
    queue<PII> q;
    q.push({
    
    0, 0});
    while (!q.empty())
    {
    
    
        PII p = q.front();
        q.pop();
        
        for (int i = 0; i < 4; i++)
        {
    
    
            int x = p.first + dx[i], y = p.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
            {
    
    
                d[x][y] = d[p.first][p.second] + 1;
                q.push({
    
    x, y});
            }
        }
    }
    cout << d[n - 1][m - 1] << endl;
}

int main()
{
    
    
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> g[i][j];
    bfs();
    return 0;
}

output path:

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;

int g[N][N], d[N][N]; // g 地图, d 距离
PII Prev[N][N]; // 记录前驱，用于输出路径
int n, m; // n x m 的矩阵

void bfs() 
{
    
    
    int dx[4] = {
    
    -1, 0, 1, 0}, dy[4] = {
    
    0, 1, 0, -1}; // 方向向量

    queue<PII> q;
    q.push({
    
    0, 0});

    memset(d, -1, sizeof d); // 初始化距离为 -1
    d[0][0] = 0; // 起点为 0

    while (!q.empty())
    {
    
    
        PII p = q.front();
        q.pop();

        for (int i = 0; i < 4; i++)
        {
    
    
            int x = p.first + dx[i], y = p.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
            {
    
    
                d[x][y] = d[p.first][p.second] + 1; // 更新距离
                q.push({
    
    x, y}); // 新坐标入队
                Prev[x][y] = p; // 更新前驱
            }
        }
    }

    // 输出路径
    int x = n - 1, y = m - 1;
    while (x || y) {
    
    
        cout << x << " " << y << endl;
        // Prev[x][y] 存储的是能到达当前位置的位置
        PII p = Prev[x][y];
        x = p.first, y = p.second;
    }

    cout << d[n - 1][m - 1] << endl;
}

int main()
{
    
    
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> g[i][j];
    bfs();
    return 0;
}

Tree and Graph Storage

A tree is a special kind of graph (acyclic connected graph).

Undirected graphs are special directed graphs, and directed graphs are mainly learned.

有向图：（两个点之间有固定的方向）
a ---> b

无向图：（实际上就是每个方向都能走）
a ---> b
b ---> a

Directed graph storage:

Adjacency matrix : two-dimensional array, high space complexity (suitable for dense graphs)
Adjacency list : use a linked list (suitable for sparse graphs)

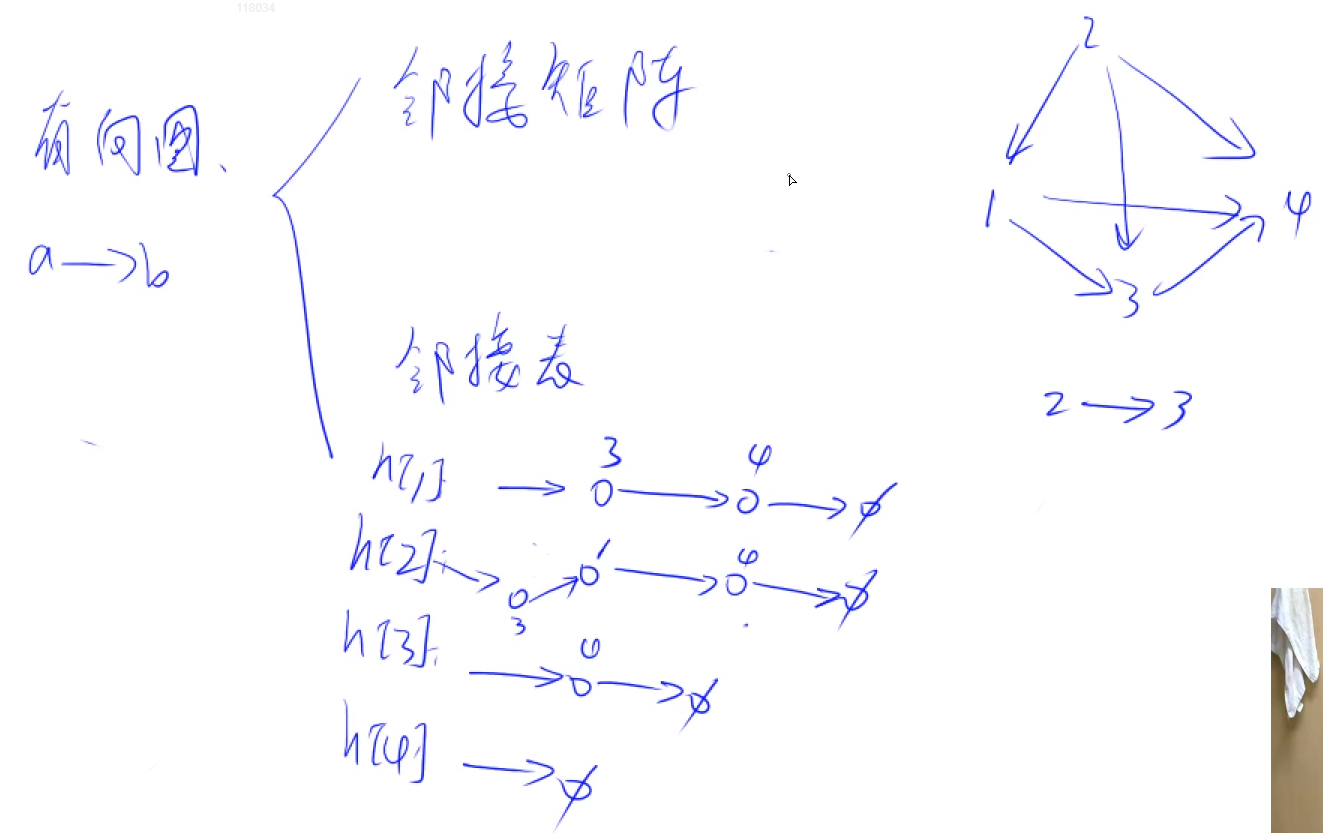
Requirements: n - the number of points in the graph, m - the number of edges in the graph

Adjacency list storage for graphs : suitable for sparse graphs (m and n are of the order of magnitude)

Unweighted graph

int h[N]; // 链表头
int e[M]; // 节点的值
int ne[M]; // 下一个节点
int idx; // 当前节点的索引

// 插入一条 a 指向 b 的边
// 在 a 对应的单链表中插入一个节点 b
void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

entitled figure

// 对于有权图，需要一个 w[] 存储权值
int h[N], e[M], ne[M], w[M], idx;

void add(int a, int b, int c)
{
    
    
	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

Graph adjacency matrix storage : suitable for dense graphs (m and n^2 are of the order of magnitude)

// g[i][j] = k 表示 i 指向 j 边长为 k
int g[N][N];

void add(int a, int b, int c)
{
    
    
	g[a][b] = min(g[a][b], c); // 处理重边，只需要记录最短的边
}

The structure used in the Bellman Ford algorithm to store edges :

// a 指向 b 权重为 w 的边
struct Edge {
    
    
	int a, b, w;
} edges[M];

Depth-first traversal of trees and graphs

DFS template:

void dfs(int u) 
{
    
    
    st[u] = true; // 标记已访问

    int sum = 1, res = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
    
    
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

center of gravity of the tree

DFS has a very good feature. It can find the size of each subtree while traversing.

Topic: 846. Center of gravity of a tree - AcWing question bank

Problem solution: AcWing 846. The center of gravity of the tree - AcWing

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = N * 2;

// 图的邻接表表示
int h[N]; // 链表头
int e[M]; // 节点的值
int ne[M]; // 下一个节点
int idx; // 当前节点的索引
bool st[N]; // 标记访问

int n;
int ans = N;

// 插入一条 a 指向 b 的边
// 在 a 对应的单链表中插入一个节点 b
void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 以 u 为根的子树点的数量
int dfs(int u) 
{
    
    
    st[u] = true; // 标记已访问

    // sum - 当前子树点的数量, res - 删除当前点后连通块的最大值
    int sum = 1, res = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
    
    
        int j = e[i];
        if (!st[j]) {
    
    
            int s = dfs(j); // 当前子树的大小
            sum += s;
            res = max(res, s);
        };
    }
    // 树的重心：删除当前点后，剩余各个连通块中点数的最大值最小
    res = max(res, n - sum);
    ans = min(ans, res); 

    return sum;
}

int main() 
{
    
    
    // 初始化链表
    memset(h, -1, sizeof h);

    cin >> n;
    for (int i = 0; i < n; i++)
    {
    
    
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }
    dfs(1);
    cout << ans << endl;
    return 0;
}

Breadth-first traversal of trees and graphs

BFS template:

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (!q.empty())
{
    
    
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
    
    
        int j = e[i];
        if (!st[j])
        {
    
    
            st[j] = true; // 表示点 j 已经被遍历过
            q.push(j);
        }
    }
}

Hierarchy of points in the graph

Topic: 847. Hierarchy of Points in a Graph - AcWing Question Bank

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
int d[N]; // 存储每个节点距离起点的距离 d[1] = 0
int n, m; // n 个点 m 条边

void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int bfs()
{
    
    
    memset(d, -1, sizeof d);
    d[1] = 0;
    
    queue<int> q;
    q.push(1);
    
    while (!q.empty())
    {
    
    
        int t = q.front();
        q.pop();
        // 遍历 t 的每个邻边
        for (int i = h[t]; i != -1; i = ne[i])
        {
    
    
            int j = e[i];
            if (d[j] == -1)
            {
    
    
                d[j] = d[t] + 1; // 存储 j 节点距离起点的举例，并标记已访问
                q.push(j);
            }
        }
    }
    return d[n];
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
    
    
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    cout << bfs() << endl; 
    return 0;
}

topological sort

In a directed acyclic graph , there must be at least one point whose in-degree is 0, and there must be a topological sequence.

The conclusion can be obtained quickly by using the method of proof by contradiction. If each point has a predecessor node, then this graph will be endless.

In-degree and out-degree:

An in-degree of 0 means that no point is required to be in the front, and all points with an in-degree of 0 can be ranked in the front.

The idea of topological sorting:

Enter the point with in-degree 0 into the queue, and then delete all the edges of the point pointed to by the point
If there are points with an in-degree of 0 after deleting the edge, then add these points to the team
Repeat the above process until the queue is empty
If there are n points in the queue at the end, the topological order can be realized

Topological Sequences of Directed Graphs

Topic: 848. Topological Sequences of Directed Graphs - AcWing Question Bank

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;

int h[N], e[N], ne[N], idx;
int q[N], hh = 0, tt = -1; // 队列Ω
int d[N]; // 入度
int n, m;

void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool topsort()
{
    
    
    // 将入度为 0 的点入队
    for (int i = 1; i <= n; i++)
        if (d[i] == 0) q[++tt] = i;
    // 不停的将入度为 0 的点指向的边删除，删除后入度为 0 则入队
    while (hh <= tt)
    {
    
    
        int t = q[hh++];
        for (int i = h[t]; i != -1; i = ne[i])
        {
    
    
            int j = e[i];
            d[j] --; // 删除 t->j 的边
            // 如果 j 的入度为 0 则入队
            if (d[j] == 0) q[++tt] = j;
        }
    }
    // n 个点的都入队则为拓扑图
    return tt == n - 1;
}

int main()
{
    
    
    memset(h, -1, sizeof h);

    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
    
    
        int a, b;
        cin >> a >> b;
        add(a, b); // 加边 a -> b
        d[b]++; // 维护 b 入度
    }
    if (topsort())
    {
    
    
        for (int i = 0; i < n; i++) cout << q[i] << " ";
        puts("");
    } else puts("-1");
    return 0;
}

shortest path

Source point == start point in graph theory , sink point == end point

Requirements: n - the number of points in the graph, m - the number of edges in the graph

Single source , the shortest path with only one origin.
Multiple sources , the shortest path from multiple different starting points to other points.

A dense graph has a large number of edges, and m and n^2 are of the same order of magnitude.
Sparse graph , refers to a small number of edges, and m and n are of the same order of magnitude.

Dijkstra

Naive Dijkstra

Dijkstra is based on greed. When there are negative weight edges, the local optimum is not necessarily the global optimum.

Topic: 849. Dijkstra Finding the Shortest Path I - AcWing Question Bank

The overall idea: perform n - 1 iterations to determine the minimum value from each point to the starting point.

The initialization distance is infinite, and the distance from the source point to the source point is 0
Do n iterations:
1. Find the point t that is closest to the source point among the points that are currently not determined to be the shortest path
2. Use t to update the distances of other points (compare the distances of 1–>j and 1–>t–>j)

Time complexity analysis:

Find the point with the shortest path: $O(n^2)$

Diagram: AcWing 849. Dijkstra Finding the Shortest Path I: Diagram Detailed Code (diagram) - AcWing

Using an adjacency matrix to write:

#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;

int g[N][N]; // 邻接矩阵（稠密图）
int dist[N]; // 到源点的距离
bool st[N]; // 记录是否已经找到最短路
int n, m; // n 个点, m 条边

int dijkstra()
{
    
    
    // 距离初始化成无穷大
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0; // 1 号点距离为 0
    
    for (int i = 0; i < n; i++)
    {
    
    
	    // 在没有确定最短路的点中，距离源点最近的点
        int t = -1;
        for (int j = 1; j <= n; j++)
            // 当前点未确定最短路 && 当前路不是最短的
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = true; // 标记已经确定最短路

        // 使用 t 更新其他点距离
        // 遍历所有 t 可以达到的点 jd
        for (int j = 1; j <= n; j++)
            // 比较 1--> j 和 1--> t --> j 的距离
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    
    
    // 默认边长初始化成无穷大
    memset(g, 0x3f, sizeof g); 
    
    cin >> n >> m;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        // 处理重边，只需要记录最短的边
        g[a][b] = min(g[a][b], c); 
    }

    cout << dijkstra() << endl;
    return 0;
}

How to write the adjacency list:

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e6 + 10;

int h[N], w[N], e[N], ne[N], idx; // 邻接表
int dist[N]; // 到源点的距离
bool st[N]; // 是否已经确认最短路
int n, m;

void add (int a, int b, int c)
{
    
    
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra()
{
    
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < n; i++)
    {
    
    
        int t = -1;
        // 找到未确定最短路的点中，距离源点最近的点 t
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        st[t] = true;
        // 使用 t 更新邻点的最短路径
        for (int j = h[t]; j != -1; j = ne[j])
        {
    
    
            int k = e[j]; // 遍历 t 的邻点
            dist[k] = min(dist[k], dist[t] + w[j]);     
        }
    }
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    cout << dijkstra() << endl;
}

Heap-optimized Dijkstra

Title: AcWing 850. Dijkstra Finding the Shortest Path II - AcWing

The heap-optimized version of Dijkstra uses the min heap to optimize the naive version for finding the shortest distance point.

The pair binary group in C++ supports comparison by default, with first as the first keyword and second as the second keyword to perform lexicographical comparison.

What is stored in the heap is a binary group {距离, 节点编号}, so as to optimize the process of finding the point with the shortest distance.

Time complexity: $O (m l o g n)$ , traversing the outgoing edges of all points is equivalent to traversing all edges, so it is m times

Adjacency list: the most suitable solution to this problem

#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int N = 1e6 + 10;
typedef pair<int, int> PII; // 堆里存储 { 距离, 节点编号 }

int h[N], w[N], e[N], ne[N], idx; // 邻接表（稀疏图）
int dist[N]; // 距离源点的距离
bool st[N]; // 是否已经找到最短路
int n, m;

// 添加 a 指向 b 边长为 c 的边
void add(int a, int b, int c)
{
    
    
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    
    
    memset(dist, 0x3f, sizeof dist); // 距离初始化为无穷大
    dist[1] = 0;
    
    priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆
    heap.push({
    
    0, 1}); // 1 号点距离源点距离为 1

    while (heap.size())
    {
    
    
        PII t = heap.top(); // 距离源点最近的点
        heap.pop();

        int ver = t.second; // 节点编号
        // int distance = t.first; // 源点距离 ver 的距离

        if (st[ver]) continue; // 如果距离已经确定，则跳过该点
        
        // 更新 ver 所指向的节点距离       
        st[ver] = true;
        for (int i = h[ver]; i != -1; i = ne[i])
        {
    
    
            int j = e[i];
			// 比较 1-->j 和 1-->ver-->j 的距离
            if (dist[j] > dist[ver] + w[i])
            {
    
    
                dist[j] = dist[ver] + w[i];
                heap.push({
    
    dist[j], j}); // 距离变小，则入堆
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    
    
    memset(h, -1, sizeof h);

    cin >> n >> m;
    while (m -- )
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c); // 邻接表不需要考虑重边
    }
    cout << dijkstra() << endl;
    return 0;
}

Adjacency matrix: If the memory is too large, an error will be reported

#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
const int N = 5500;
typedef pair<int, int> PII; // {距离, 节点编号}

int g[N][N]; // 邻接矩阵
int dist[N], st[N];
int n, m;

int dijkstra()
{
    
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆
    heap.push({
    
    0, 1});
    
    while (heap.size())
    {
    
    
        PII t = heap.top();
        heap.pop();
        
        int ver = t.second; // 距离源点最近的点
        if (st[ver]) continue;
        
        // 利用 t 更新它的邻点
        st[ver] = true; 
        for (int i = 1; i <= n; i++)
        {
    
    
            // 比较 1->i 和 1->ver->i
            if (dist[i] > dist[ver] + g[ver][i])
            {
    
    
                dist[i] = dist[ver] + g[ver][i];
                heap.push({
    
    dist[i], i});
            }
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main()
{
    
    
    memset(g, 0x3f, sizeof g);
    cin >> n >> m;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c); // 处理重边
    }
    cout << dijkstra() << endl;
    return 0;
}

Bellman-Ford

The bellman-ford algorithm is good at solving shortest path problems with limited number of edges .

Topic: 853. Shortest path with limited number of edges - AcWing Question Bank

The edge weight of this question may be negative, so Dijkstra cannot be used .
Reference: AcWing 853. Shortest path with limited number of edges - AcWing
Dijkstra cannot solve negative weight edges because Dijkstra requires that after each point is determined st[j] = true, dist[j]it is the shortest distance, and it cannot be updated afterwards (one-shot sale), and If there are negative weight edges, then the determined point is dist[j]not necessarily the shortest.

Idea: Perform relaxation continuously, and update each edge each time it is relaxed. If it can be updated after n - 1 relaxations, it means that there is a negative cycle in the graph, and the result cannot be obtained, otherwise it is completed.

step:

// back 数组是上一次迭代后 dist 数组的备份。
for n 次
	for 所有边 a,b,w (松弛操作)
		dist[b] = min(dist[b], back[a] + w)

Time complexity: $O (nm)$

Why do you need the back array?

Ref: AcWing 853. Shortest Path with Edge Limits - AcWing

In order to avoid the following concatenation situation, when the number of edges is limited to one , the distance of node 3 should be 3, but due to the concatenation situation, the distance of node 3 is updated with node 2 updated in this round, so the distance of node 3 is now is 2.
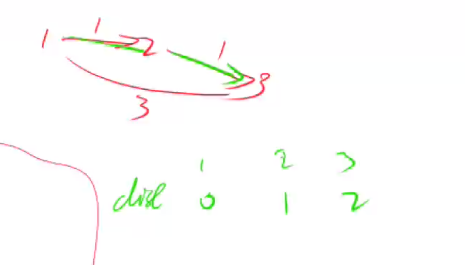
The correct way is to use the update distance of node 2 in the last round - infinity, to update node 3, and then take the minimum value, so the distance between node 3 and the starting point is 3.

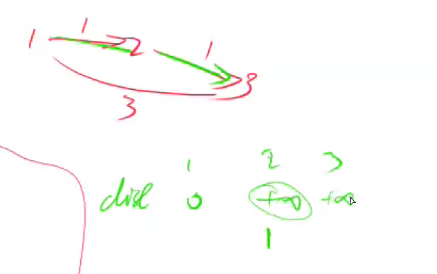
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, M = 10010;

int dist[N]; // 到源点的距离
int backup[N]; // 备份数组防止串联
int n, m, k;

// a 指向 b 权重为 w 的边
struct Edge {
    
    
    int a, b, w;
} edges[M];

void bellman_ford()
{
    
    
    // 初始化距离为无穷大
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0; // 源点到源点距离为 0

    for (int i = 0; i < k; i++)
    {
    
    
		// 备份上一次迭代的结果，防止出现串联（用本次更新的点去更新其他点）
	    memcpy(backup, dist, sizeof dist);
        for (int j = 0; j < m; j++) // 遍历所有边
        {
    
    
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
			// 比较 1->b 和 1->a->b 的路径长度
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");
    else cout << dist[n] << endl;
}

int main()
{
    
    
    cin >> n >> m >> k;
    for (int i = 0; i < m; i++)
    {
    
    
        int a, b, w; 
        cin >> a >> b >> w;
        edges[i] = {
    
    a, b, w};
    }
    bellman_ford();
    return 0;
}

SPFA

The limitation of SPFA is very small, as long as there are no negative cycles in the graph, it can be used. SPFA can handle not only negative weight graphs, but also positive weight graphs.

SPFA can be seen as an optimization of Bellman_ford:

Bellman_ford will traverse all edges (fixed $O (nm)$ ), the traversal of many edges is meaningless, only need to traverse the edges connected by the points whose distance to the source point is small.

st[]Arrays in SPFA and Dijkstra :

st[]In Dijkstra, the point that is currently determined to be the shortest distance to the source point is saved, and it is irreversible after determination.

The in SPFA st[]only represents the point that has been updated currently, and it is reversible.

Thoughts from SPFA and Dijksra :

Dijkstra is based on the idea of greed . Each time the nearest point is selected to update other points, it will not be visited afterwards.

In SPFA, as long as the distance of a certain point is updated, it will be added to the queue to update other points, and each point may be added to the queue repeatedly.

SPFA finds the shortest path

Topic: 851. spfa find the shortest path - AcWing question bank

Reference: AcWing 851. $\color{green}{spfa seek the shortest path --- diagram + detailed code comment}$ - AcWing

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5 + 10;

int h[N], w[N], e[N], ne[N], idx; // 邻接表存储
int dist[N]; // 距离源点的距离
bool st[N]; // 每个点是否在队列中
int n, m;

// 添加一条 a 指向 b 权重为 c 的边
void add (int a, int b, int c)
{
    
    
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 求 1 号点到 n 号点的最短路距离
void spfa()
{
    
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    queue<int> q;
    q.push(1);
    st[1] = true;
    
    while (q.size())
    {
    
    
        int a = q.front();
        q.pop();
        st[a] = false;
        // 遍历 a 的出边指向的点
        for (int i = h[a]; i != -1; i = ne[i])
        {
    
    
            int b = e[i], c = w[i];
            if (dist[b] > dist[a] + c)
            {
    
    
                dist[b] = dist[a] + c;
                if (!st[b])
                {
    
    
                    q.push(b);
                    st[b] = true;
                }
            }
        }
    }
    if (dist[n] == 0x3f3f3f3f) puts("impossible");
    else cout << dist[n] << endl;
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        add (a, b, c);
    }
    spfa();
    return 0;
}

SPFA Judgment Negative Loop

Topic: 852. spfa judgment negative ring - AcWing question bank

Common methods for finding negative rings, based on SPFA, generally use method 2 (this question also uses method 2):

Method 1: Count the number of times each point enters the queue. If a certain point enters the queue n times, it means that there is a negative cycle.
Method 2: Count the number of edges contained in the shortest path of each point. If the shortest path of a point If the number of edges contained is greater than or equal to n, it also indicates that there is a cycle

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5 + 10;

int h[N], w[N], e[N], ne[N], idx; // 邻接表存储
int dist[N]; // 每个点距离源点的距离
int cnt[N]; // 每个点到源点的边数
bool st[N]; // 每个点是否在队列中
int n, m;

// 添加一条 a 指向 b 权重为 c 的边
void add (int a, int b, int c)
{
    
    
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 求 1 号点到 n 号点的最短路距离
bool spfa()
{
    
    
    queue<int> q;
    
    // 判断负环，只从一个点出发，有可能到达不了负环那里
    // 需要一开始就把所有结点放入队列，且标记进入了队列提高效率
    for (int i = 1; i <= n; i++)
    {
    
    
        q.push(i);
        st[i] = true;
    }
    
    while (q.size())
    {
    
    
        int a = q.front();
        q.pop();
        st[a] = false;
        // 遍历 a 的出边指向的点
        for (int i = h[a]; i != -1; i = ne[i])
        {
    
    
            int b = e[i], c = w[i];
            if (dist[b] > dist[a] + c)
            {
    
    
                dist[b] = dist[a] + c;
                cnt[b] = cnt[a] + 1;
                if (cnt[b] >= n) return true;
                if (!st[b])
                {
    
    
                    q.push(b);
                    st[b] = true;
                }
            }
        }
    }
    return false;
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        add (a, b, c);
    }
    puts(spfa() ? "Yes" : "No");
    return 0;
}

Floyd

Floyd belongs to the multi-source shortest path , can find the shortest path between any two vertices, and supports negative weight edges (no negative weight loops).

Time complexity: $O(n^3)$ , the efficiency is better than executing Dijkstra's algorithm n times.

The single-source shortest path algorithm calculates once for each vertex, and can also find the shortest path between any two vertices.

Algorithm process:

Initialize d[][]the array , pay attention to the situation of dealing with self-loops and multiple edges
k, i, j triple loop to update d[][]the array

Principle: dynamic programming
$f [k] [i] [j]$ represents (the value range of k is from 1 to n), when considering the node from 1 to k as the intermediate node, the shortest path from i to j.
State transition equation: $f [k] [i] [j] = min (f [k - 1] [i] [j], f [k - 1] [i] [k] + f [k - 1] [k] [j])$

Title: AcWing 854. Floyd Finding the Shortest Path - AcWing

#include <iostream>
#include <cstring>
using namespace std;
const int N = 210, M = 20010, INF = 0x3f3f3f3f;

// d[i][j] 表示从 i 到 j 的最短路径
int d[N][N]; 
int n, m, k;

void floyd()
{
    
    
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main()
{
    
    
    cin >> n >> m >> k;
    // 初始化
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) d[i][j] = 0; // 处理自环
            else d[i][j] = INF;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        d[a][b] = min(d[a][b], c); // 处理重边
    }
    floyd();
    while (k --)
    {
    
    
        int a, b;
        cin >> a >> b;
        if (d[a][b] > INF / 2) puts("impossible");
        else cout << d[a][b] << endl;
    }
    return 0;
}

minimum spanning tree

m - the number of edges, n - the number of points
Dense graphs: m and n^2 are of the order of magnitude
Sparse graphs: m and n are of the order of magnitude

Kruskal is simpler to use than heap-optimized Prims, so heap-optimized Prims are not commonly used.

Simple Prim

Given an undirected graph, select several edges in the graph to connect all the nodes of the graph, requiring the minimum sum of edge lengths, which is the minimum spanning tree.

the whole idea:

Initialize the distance to infinity
Do n iterations:
1. Find a point t that is not yet connected, but is closest to the connected part
2. Use t to update other points toconnected partdistance

Dijkstra is to use t to update the distance from other points to the source point

Topic: 858. Prim's Algorithm for Finding the Minimum Spanning Tree - AcWing Question Bank

Solution: AcWing 858. Prim's Algorithm for Minimum Spanning Tree: Diagram + Detailed Code Comments (with save path) - AcWing

#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;

int g[N][N]; // 稠密图
int dist[N]; // 节点到生成树的距离
bool st[N]; // 节点是否在生成树中
int n, m;

// 返回最小生成树中边权之和
int prim()
{
    
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0; // 从 1 号点开始生成
    
    int res = 0;
    // 每次循环选出一个点加入到生成树中
    for (int i = 0; i < n; i++)
    {
    
    
        // 找到集合外，距离集合最小的点
        int t = -1;
        for (int j = 1; j <= n; j++) // 遍历所有节点
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        // 当前图是不连通的，不存在生成树
        if (dist[t] == INF) return INF;
        res += dist[t]; // 先更新最小生成树的边权和，防止有自环
        // 更新生成树外的点到生成树的距离
        for (int j = 1; j <= n; j++) 
            // t->j 距离小于原来的距离，则更新
            dist[j] = min(dist[j], g[t][j]);
        st[t] = true; // 标记该点已经在生成树中
    }
    return res;
}

int main()
{
    
    
    // 各个点之间的距离初始化成无穷
    memset(g, 0x3f, sizeof g);
    
    cin >> n >> m;
    while (m --)
    {
    
    
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c); // 无向图，有重边
    }
    
    int t = prim(); // 求最小生成树

    if (t == INF) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

Heap-optimized Prim

This section is skipped for the following reasons:

Heap-optimized Prim works exactly the same way as heap-optimized Dijkstra.
For minimum spanning trees, Kruskal's algorithm is simpler and more efficient.

Kruskal

Video explanation: Minimum spanning tree (Kruskal (Kruskal) and Prim (Prim)) algorithm animation demonstration_哔哩哔哩_bilibili

Kruskal's algorithm:

Sort all edges by weight from small to large O(mlogm)
Enumerate each edge a -> b from small to large.
- If this edge and the previous edge will not form a loop , select this edge, otherwise discard it.
- Until the connected network with n vertices filters out n - 1 edges.
- The filtered edges and all vertices constitute the minimum spanning tree of this connected network.

The method of judging whether a loop will be generated is: use union search.

In the initial state, each vertex is in a different set.
Traverse each edge of the process to determine whether the two vertices are in a set.
If the two vertices on the edge are in a set, it means that the two vertices are already connected, and this edge does not. If not in a set, ask for the edge.

Topic: 859. Kruskal Algorithm Finding Minimum Spanning Tree - AcWing Question Bank

Illustration: AcWing 859. $\color{green}{Detailed Ideas + Code Comments + Illustrations}$ - AcWing

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10, INF = 0x3f3f3f3f;

int p[N]; // 并查集
int n, m;

struct Edge {
    
    
    int a, b, w;
    // 重载 < 符号，方便调用排序函数
    bool operator < (const Edge &W) const
    {
    
    
        return w < W.w;
    }
} edges[N]; 

// 并查集，找祖宗节点
int find(int x)
{
    
    
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    
    
    int cnt = 0; // 全部加入到树的集合中边的数量(可能有多个集合)
    int res = 0; // 最小生成树的边权重之和
    
    // 按边权从小到大顺序遍历所有边
    for (int i = 0; i < m; i++)
    {
    
    
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        int pa = find(a), pb = find(b);
        if (pa != pb) // a b 不在一个集合中
        {
    
    
            p[pa] = p[pb]; // 合并 a b 
            res += w; // 计算边权和     
            cnt ++; // 全部集合中的边数量 + 1
        }
    }
    
    // 树中有 n 个节点便有 n-1 条边，如果 cnt 不等于 n-1，说明无法生成有 n 个节点的树
    if (cnt < n - 1) return INF; // 无法生成最小生成树
    return res;
}

int main()
{
    
    
    cin >> n >> m; 
    // 初始化并查集
    for (int i = 0; i < n; i++) p[i] = i;
    // 建图
    for (int i = 0; i < m; i++)
    {
    
    
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {
    
    a, b, w};
    }
    // 按照边权升序排序
    sort(edges, edges + m);
    
    int t = kruskal();
    if (t == INF) puts("impossible");
    else cout << t;
    
    return 0;
}

binary picture

A bipartite graph is bipartite if and only if there are no odd cycles in the graph. Since there are no odd-numbered cycles in the graph, there must be no contradictions in the coloring process.

Bipartite graph: must not contain odd rings, may contain rings of even length, not necessarily a connected graph

Easy-to-understand definition: the points in the figure can be divided into left and right parts by moving, the points on the left are only connected to the points on the right, and the points on the right are only connected to the points on the left.

The following figure is a bipartite graph:

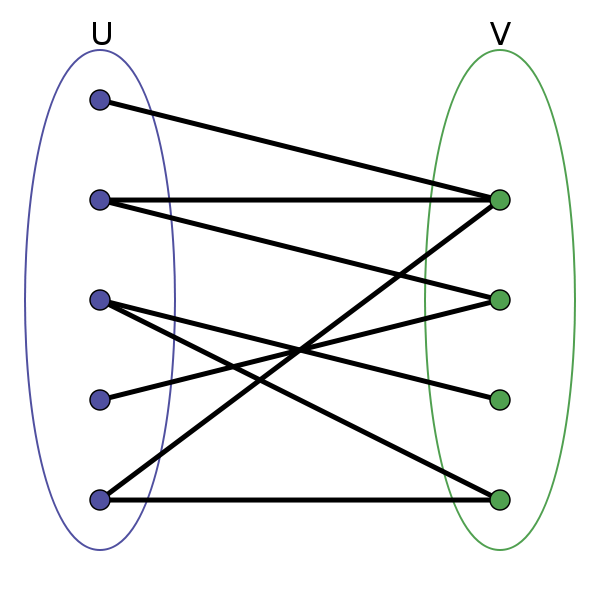
The following graph is not bipartite:

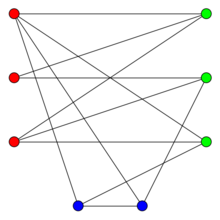
Dyeing

DFS code idea:

Colors 1and 2represent different colors and 0represent undyed
Traverse all points, and perform DFS on undyed points each time (the default color is 1 or 2)
- If its adjacent edge is uncolored, perform DFS coloring on its adjacent edge
- If its adjacent edge has been colored, determine whether the color is 3 - c

Because the success of a certain point dyeing does not mean that the whole graph is a bipartite graph, so only a certain point dyeing failure can be immediately break / return
- dyeing failure is equivalent to the existence of two adjacent points dyed the same color

Title: 860. Coloring method to determine bipartite graph-AcWing question bank

#include <iostream>
#include <cstring>
using namespace std;
// 由于是无向图，顶点数最大是 N，那么边数最大是顶点数的 2 倍
const int N = 1e5 + 10, M = N + N;

int h[N], e[M], ne[M], idx;
// 记录节点被染成哪种颜色, 0 表示未染色, 1, 2 是两种不同的颜色
int color[N];
int n, m;

void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 深度优先遍历对 u 及其邻点进行染色，并返回是否能够完成染色操作
bool dfs(int u, int c)
{
    
    
    color[u] = c; // 对 u 染色
    // 遍历 u 所有邻点并染色
    for (int i = h[u]; i != -1; i = ne[i])
    {
    
    
        int j = e[i];
        // 邻点没有颜色，则递归处理这个邻点(1 染成 2，2 染成 1)
        if (!color[j] && !dfs(j, 3 - c))
            return false;
        // 已经染色，且颜色不是 3 - c，则冲突
        else if (color[j] && color[j] != 3 - c)
            return false;   
    }
    return true;
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    cin >> n >> m;
    // 读入边
    for (int i = 0; i < m; i++)
    {
    
    
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); // 无向图
    }
    
    for (int i = 1; i <= n; i++) // 遍历所有点
        if (!color[i]) // 没有染色
        {
    
    
            if (!dfs(i, 1)) // 染色该点，并递归处理和它相邻的点
            {
    
    
                puts("No");
                return 0;
            }
        }
    puts("Yes");
    return 0;
}

BFS code idea:

Colors 1and 2represent different colors and 0represent undyed
define queuesavePII<点编号, 颜色>
遍历所有点，将未染色的点都进行 BFS
队列初始化将第 i 个点入队（默认颜色可以是 1 或 2）
- while (队列不空)
- 每次获取队头 t，并遍历队头 t 的所有邻边
  - 若邻边的点未染色，则染上与队头 t 相反的颜色，并添加到队列
  - 若邻边的点已经染色且与队头 t 的颜色相同, 则返回 false

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;

int e[M], ne[M], h[N], idx;
int n, m;
int color[N];

void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 对 u 进行染色，并对其邻边进行染色
bool bfs(int u)
{
    
    
    queue<int> q;
    q.push(u);
    color[u] = 1;

    while (q.size())
    {
    
    
        int t = q.front();
        q.pop();
        int c = color[t]; // 颜色

        for (int i = h[t]; i != -1; i = ne[i])
        {
    
    
            int j = e[i];
            // 未染色
            if (!color[j])
            {
    
    
                color[j] = 3 - c;
                q.push(j);
            }
            // 已染色且与 t 颜色相同
            else if (color[j] && color[j] == c)
                return false;
        }
    }

    return true;
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m--)
    {
    
    
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    bool flag = true;
    for (int i = 1; i <= n; i++)
    {
    
    
        if (!color[i])
        {
    
    
            if (!bfs(i))
            {
    
    
                flag = false;
                break;
            }
        }
    }
    puts(flag ? "Yes" : "No");

    return 0;
}

匈牙利算法

有趣的示例：匈牙利算法（简单易懂）_一只大秀逗的博客-CSDN博客

题目：861. 二分图的最大匹配 - AcWing题库

题解：AcWing 861. 二分图的最大匹配 - AcWing

#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, M = 1e5 + 10;

int h[N], e[M], ne[M], idx;
// st[j] = a 表示一轮模拟匹配中，女孩 j 被男孩 a 预定了
bool st[N];
// match[j] = a 表示女孩 j 现有配对男友是 a
int match[N];
// n1 n2 分别是两个点集的个数
int n1, n2, m;

void add(int a, int b)
{
    
    
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 如果 x 参与模拟配对，会不会使匹配数增多
bool find(int x)
{
    
    
    // 遍历 x 喜欢的女孩
    for (int i = h[x]; i != -1; i = ne[i])
    {
    
    
        int j = e[i]; // x 喜欢的女孩 j
        if (!st[j]) // 如果这轮匹配中，女孩 j 未被预定
        {
    
    
            st[j] = true; // x 预定女孩 j
            // 如果女孩 j 没有男朋友，或她原来的男朋友能够预定其他喜欢的女孩，则配对成功
            if (!match[j] || find(match[j]))
            {
    
    
                match[j] = x;
                return true;
            }
        }
    }
    // 自己喜欢的女孩全部被预定了，配对失败
    return false; 
}

int main()
{
    
    
    memset(h, -1, sizeof h);
    cin >> n1 >> n2 >> m;
    while (m--)
    {
    
    
        int a, b;
        cin >> a >> b;
        add(a, b); // 存边只存一条边即可，虽然是无向图
    }
    
    int res = 0;
    for (int i = 1; i <= n1; i++)
    {
    
    
        // 每次模拟匹配的预定情况都不一样，每轮都需要初始化
        memset(st, false, sizeof st);
        if (find(i)) res++;
    }
    cout << res << endl;
    return 0;
}

[AcWing Learning] Graph Theory and Search