Merge sort of eight sorting algorithms (recursive implementation + non-recursive implementation)

Table of contents

1. The basic idea of ​​merge sort

Merge sort algorithm idea (ascending order as an example)

2. Merge of two ordered subsequences (in the same array) (in ascending order)

Merge operation code of two ordered sequences:

3. Recursive implementation of merge sort

Implementation of recursive recursion and sorting: (post-order traversal recursion)

Abstract analysis of recursive function: 

4. Implementation of non-recursive recursive sorting

1. Non-recursive recursive sorting algorithm idea:

2. Algorithm implementation

Preliminary non-recursive merge sort function:

In general (the number of elements in the sorted array is not edited) Boundary condition analysis:

Bounds corrected non-recursive merge sort function

Sorting test:

---

1. The basic idea of ​​merge sort

• Merge sort is an efficient sorting algorithm designed based on divide and conquer ideas and merge operations
• The so-called merge operation is the operation of merging two ordered subsequences into one ordered sequence ( the time complexity of the merge operation algorithm is O(N+M) , and N+M is the number of elements in the two subarrays respectively )

Merge sort algorithm idea (ascending order as an example)

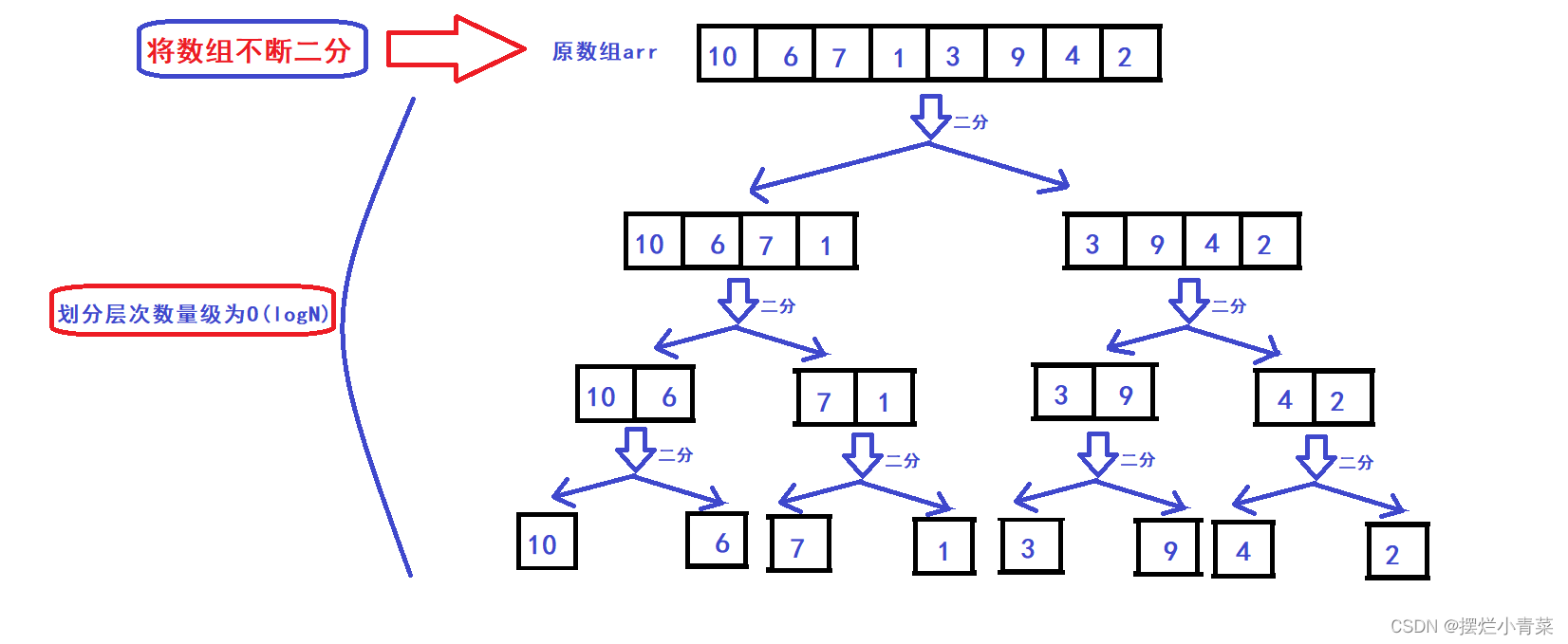
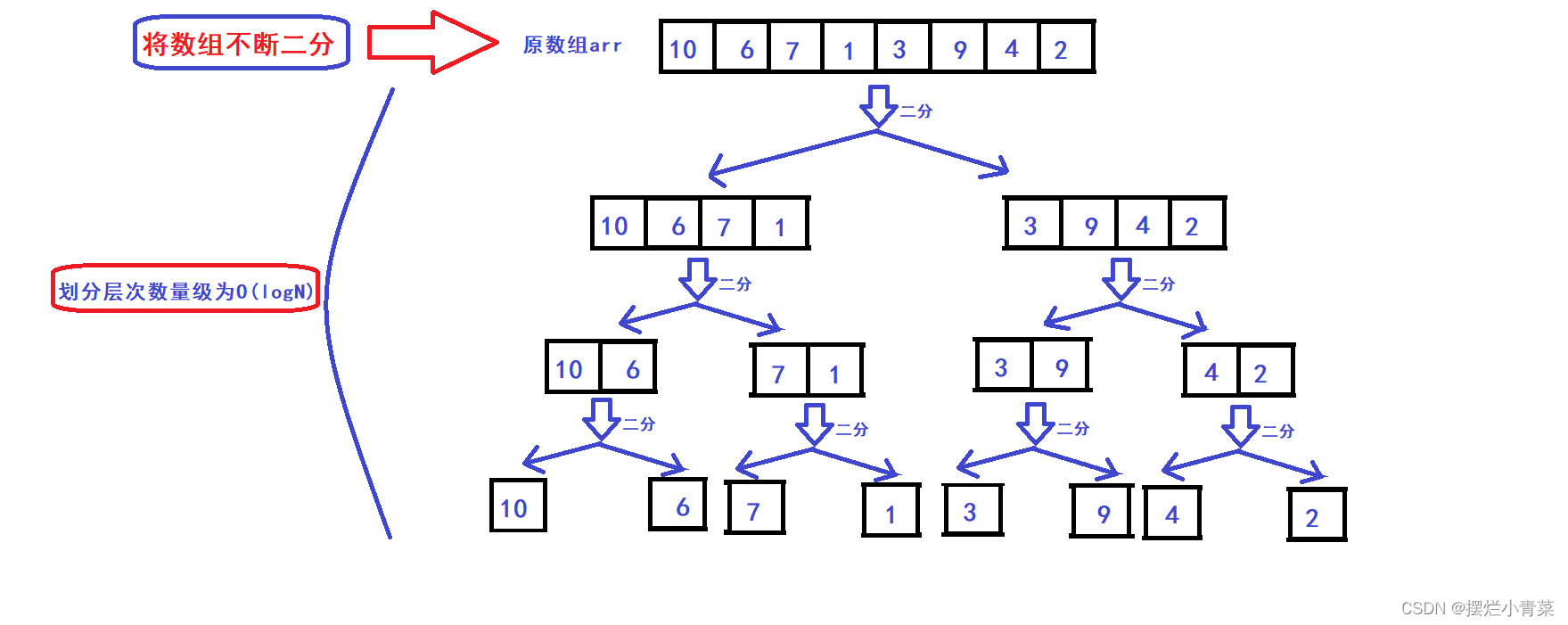
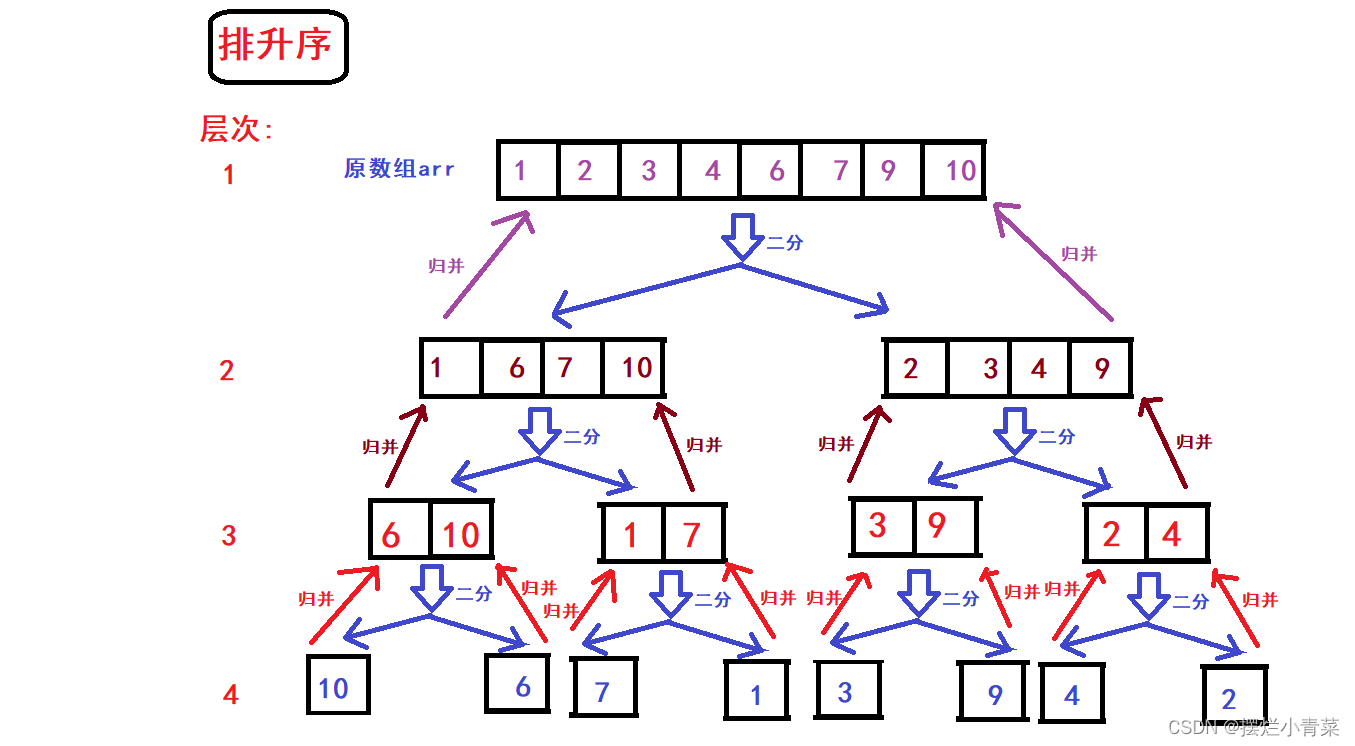
1. Assuming that the array has N elements , the array is divided into two continuously until the array is divided into N sub-arrays composed of single elements. During the entire division process , all sub-arrays form a logical structure of a full binary tree ( or close to a full binary tree ) , such as picture:
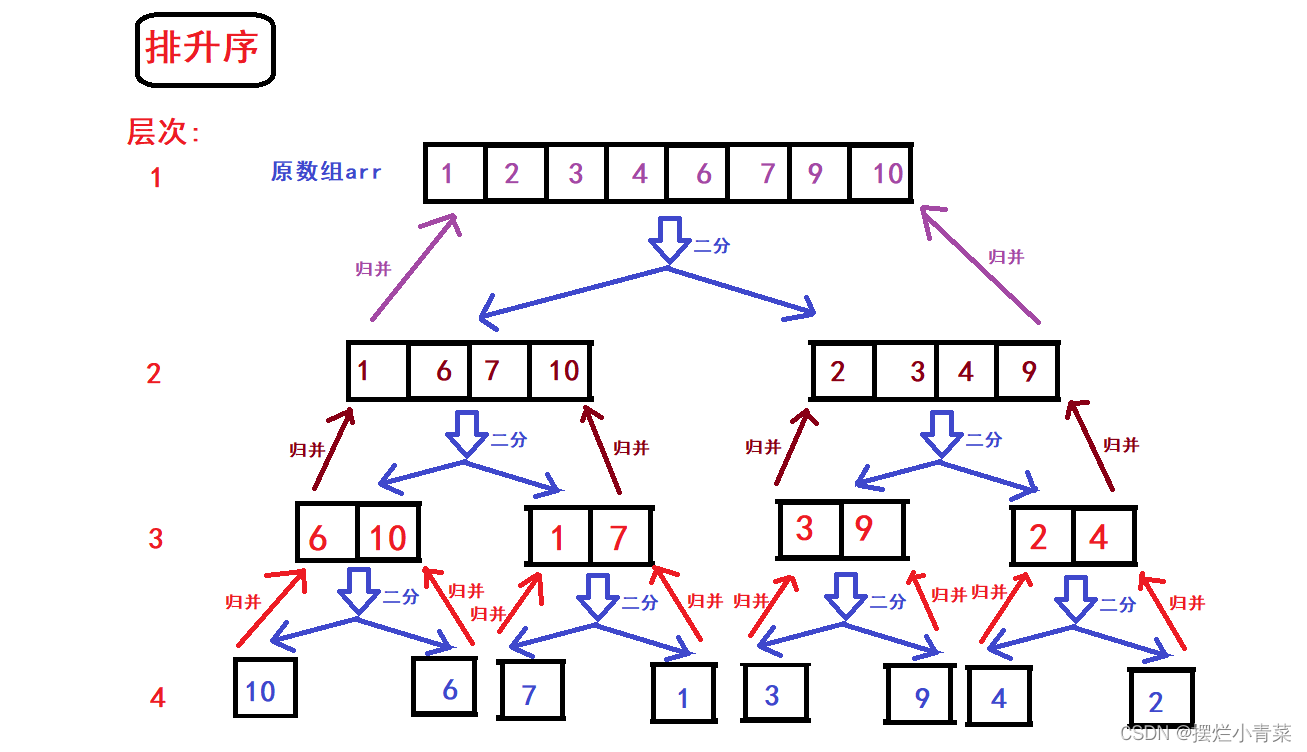
2. After the array is divided, the binary tree brother node sub-arrays (with the same precursor structure) are merged and sorted layer by layer:
3. The time complexity of the merge operation algorithm is O(M1+M2) , and M1+M2 is the number of elements of the two sub-arrays respectively , so the total time complexity of the pairwise merge operation of the sub-arrays in the first layer of the binary tree is O(N) ( N represents the number of elements in the original array ), and the order of magnitude of the full binary tree is O(logN) , so the overall time complexity of merge sorting is O(NlogN)
4. Since the array division of merge sort is strictly dichotomized each time , the sub-array division structure of each sort ( no matter what sequence it faces ) is a stable full binary tree ( or close to full binary tree ) structure , so the time of merge sort The complexity will not change under various circumstances ( it will not change the time complexity of the algorithm due to the difference in the inverse sequence number of the processed sequence like quick sort and Hill sort )
5. However, since the merge operation of the ordered sequence needs to open up an additional array to complete, the merge sort has a large space consumption, which is a defect of the merge sort

2. Merge of two ordered subsequences (in the same array) (in ascending order)

Function header:

void MergeSort(int* arr,int* tem, int left,int right)

arr is the original array to be split , tem is the temporary array for merging operation , left is the left end subscript of arr , right is the right end subscript of arr

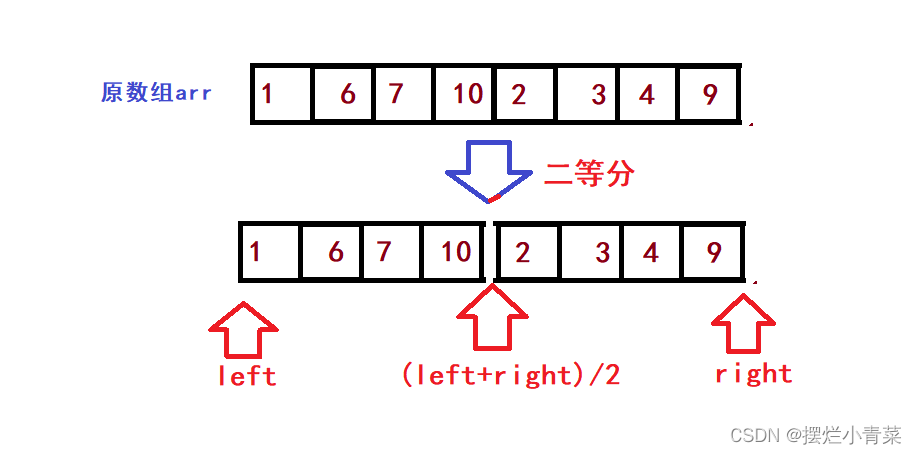
• Suppose the array arr is bisected into two subsequences ( both subsequences are ordered ):
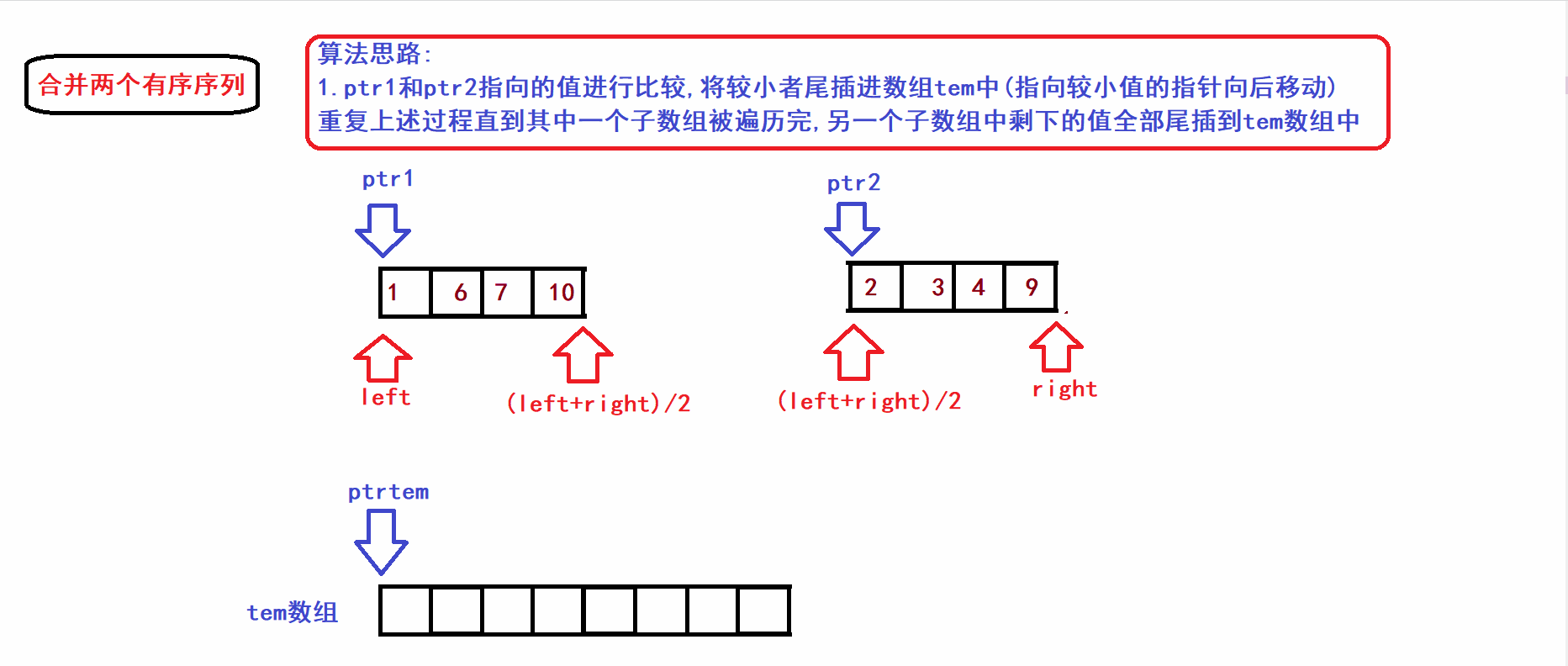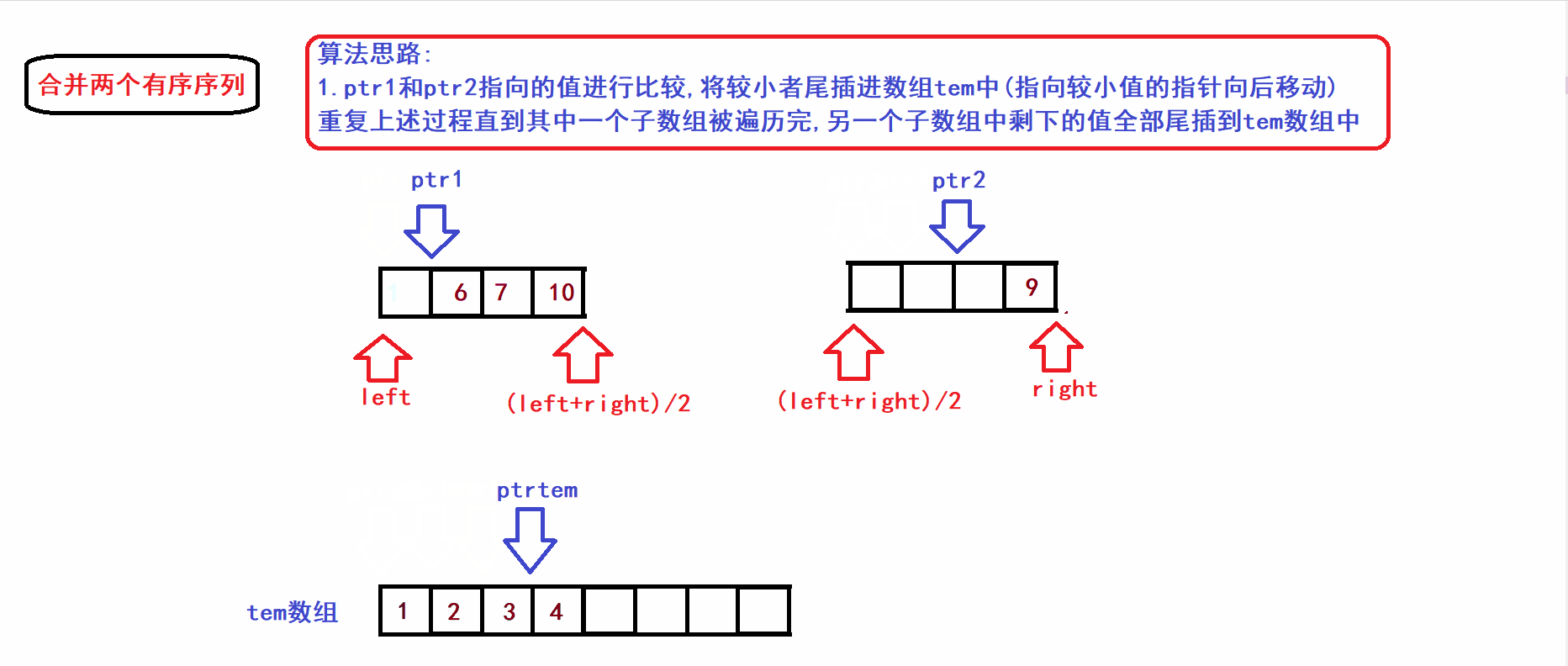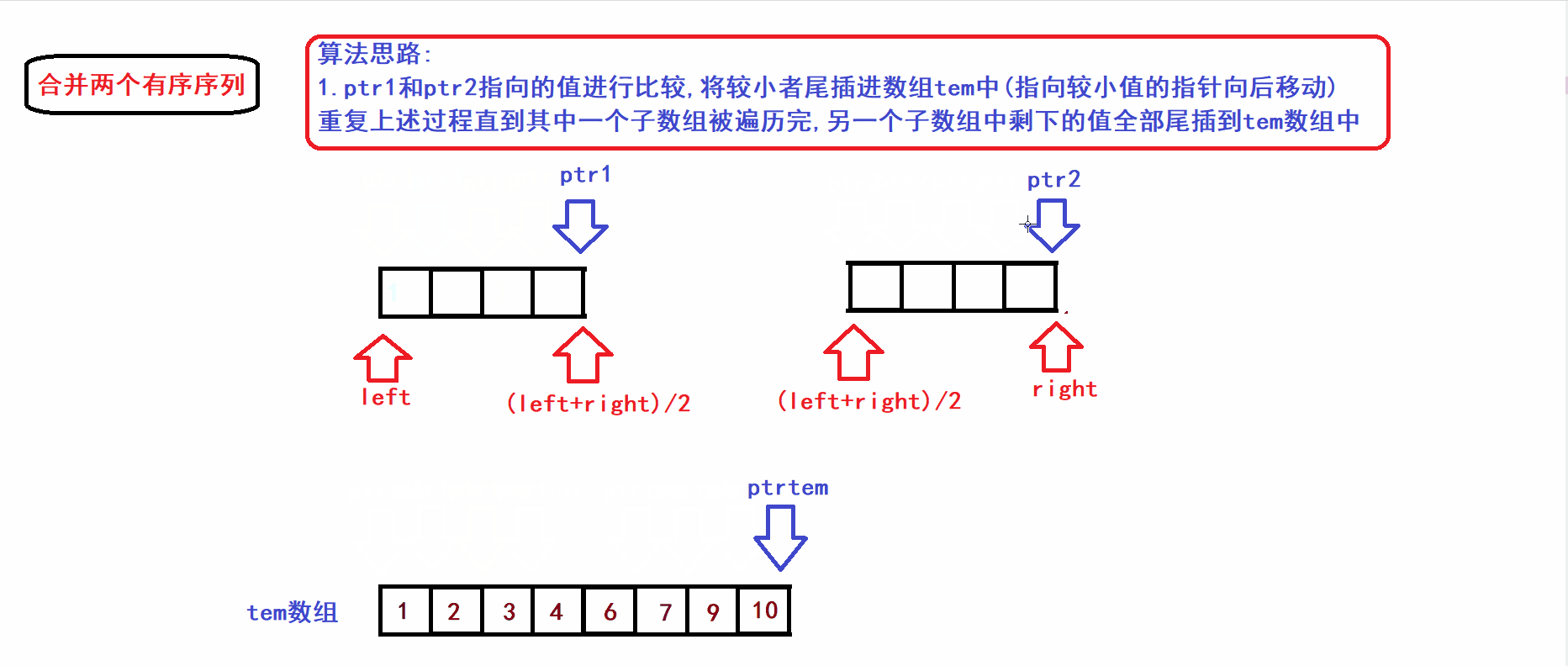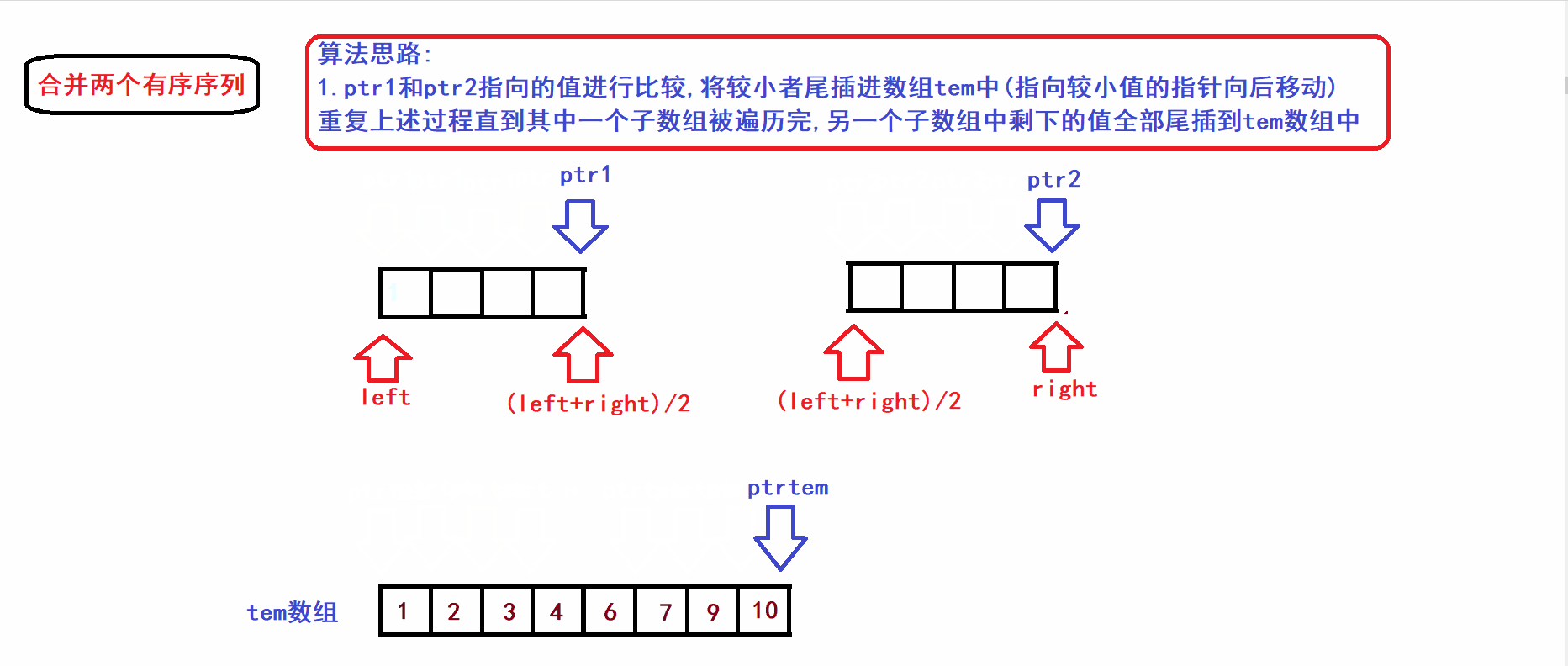
• Next, we merge the two subsequences (ordered) of [left, (left+right)/2) and [(left+right)/2), right) in the above figure into a tem array to form a new Ordinal sequence (merge is completed using three-pointer operation):
• It is not difficult to see from the algorithm gif that the time complexity of the merge operation is linearly related to the number of elements in the two sub-arrays

Merge operation code of two ordered sequences:

void MergeSort(int* arr,int* tem, int left,int right)
{
	int mid = left + (right - left) / 2;			//找到数组[left,right]的中间分割点

	int ptr1 = left;								//ptr1指向左子数组的首元素
	int ptr2 = mid;									//ptr2指向右子数组的首元素
	int ptrtem = left;                              //ptrtem用于在tem数组中尾插数据
	while (ptr1 < mid && ptr2 < right)				//ptr1和ptr2其中一个遍历完子数组就停止循环
	{
		//将较小元素尾插进tem数组中
		if (arr[ptr1] > arr[ptr2])
		{
			tem[ptrtem] = arr[ptr2];
			++ptrtem;
			++ptr2;
		}
		else
		{
			tem[ptrtem] = arr[ptr1];
			++ptrtem;
			++ptr1;
		}
	}
	//将未被遍历完的子数组剩下的元素尾插到tem数组中
	while (ptr1 < mid)
	{
		tem[ptrtem] = arr[ptr1];
		++ptrtem;
		++ptr1;
	}
	while (ptr2 < right)
	{
		tem[ptrtem] = arr[ptr2];
		++ptrtem;
		++ptr2;
	}
	
	//将归并好的有序序列拷贝到原数组arr上
	for (int i = left; i < right; ++i)
	{
		arr[i] = tem[i];
	}
}

3. Recursive implementation of merge sort

Recursive function header:

void MergeSort(int* arr,int* tem, int left,int right)

arr is the original array to be split , tem is the temporary array for merging operation , left is the left end subscript of the arr subarray , right is the right end subscript of the arr subarray

• Before merging the sub-arrays in pairs , we first need to divide the array in two :
• We can complete the entire bisection process of the array through divide-and-conquer recursion ( the subscripts of the interval endpoints of each sub-array are stored in each function stack frame of the recursive function ): ( recursive framework for array bisection )

  void MergeSort(int* arr, int* tem, int left, int right)
  {
  	if (right <= left+1)                  //当子数组只剩一个元素时停止划分
  	{
  		return;
  	}
  	int mid = left + (right - left) / 2;
  	MergeSort(arr, tem, left, mid);      //划分出的左子数组
  	MergeSort(arr, tem, mid, right);     //划分出的右子数组
  
  	//左右子数组都有序后完成左右子数组的归并
  }

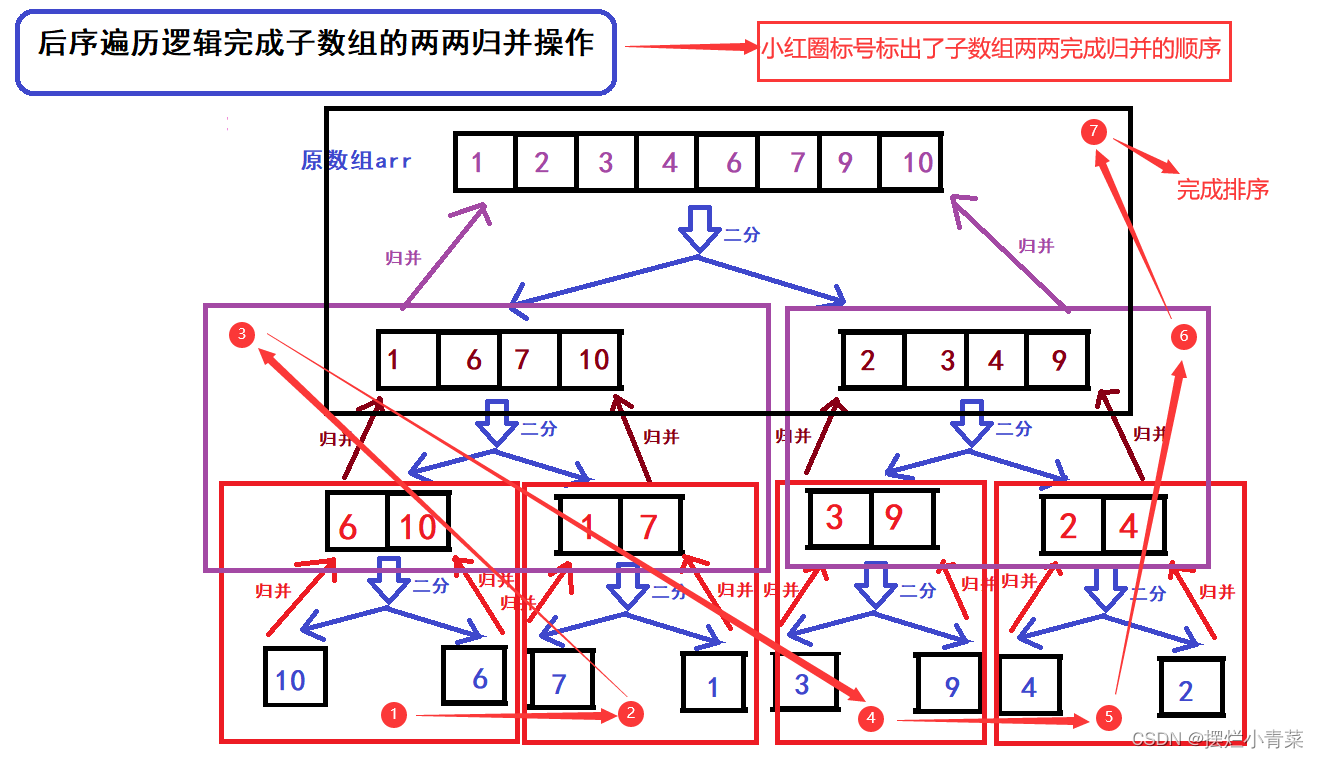
• Observing the recursive diagram , the process of pairwise merging of ordered sequences can only occur in the 7th, 13th, 14th, 21st, 27th, 28th, and 29th steps in the above figure , so the entire sorting process satisfies divide and conquer Recursive post-order traversal logic

• 

Implementation of recursive recursion and sorting: (post-order traversal recursion)

• The code segment for the (ordered) merging of the left and right subarrays is located after the two recursive statements in the function

void MergeSort(int* arr, int* tem, int left, int right)
{
	if (right <= left+1)                  //当子数组只剩一个元素时停止划分
	{
		return;
	}
	int mid = left + (right - left) / 2;
	MergeSort(arr, tem, left, mid);      //划分出的左子数组
	MergeSort(arr, tem, mid, right);     //划分出的右子数组
    
    
    //后序遍历,归并过程发生在两个递归语句之后
	//左右子数组都有序后完成左右子数组的归并
	int ptr1 = left;								//ptr1指向左子数组的首元素
	int ptr2 = mid;									//ptr2指向右子数组的首元素
	int ptrtem = left;                              //ptrtem用于在tem数组中尾插数据
	while (ptr1 < mid && ptr2 < right)				//ptr1和ptr2其中一个遍历完子数组就停止循环
	{
		//将较小元素尾插进tem数组中
		if (arr[ptr1] > arr[ptr2])
		{
			tem[ptrtem] = arr[ptr2];
			++ptrtem;
			++ptr2;
		}
		else
		{
			tem[ptrtem] = arr[ptr1];
			++ptrtem;
			++ptr1;
		}
	}
	//将未被遍历完的子数组剩下的元素尾插到tem数组中
	while (ptr1 < mid)
	{
		tem[ptrtem] = arr[ptr1];
		++ptrtem;
		++ptr1;
	}
	while (ptr2 < right)
	{
		tem[ptrtem] = arr[ptr2];
		++ptrtem;
		++ptr2;
	}

	//将归并好的有序序列拷贝到原数组arr(相应下标位置)
	for (int i = left; i < right; ++i)
	{
		arr[i] = tem[i];
	}
}

• Attention to detail: 

Abstract analysis of recursive function: 

• The recursive function MergeSort(arr, tem, left, right) can be abstracted as: use the tem array to complete the sorting process of the arr array [left, right) interval sequence
• So the recursive formula can be abstracted : MergeSort(arr,tem,left,right) = MergeSort(arr,tem,left, left + (right - left) / 2 ) + MergeSort(arr,tem, left + (right - left ) / 2,right ) + { ordered merge of subarray [left,left + (right - left) / 2)) and subarray [left + (right - left) / 2,right) }
• The meaning of the recursive formula is: the process of completing the sorting of the arr array [left, right) interval sequence can be divided into the following three steps :

1. Complete the sorting of the left subinterval [ left, left + (right - left) / 2) first
2. Then complete the sorting of the right sub-interval [ left + (right - left) / 2, right)
3. Finally, the left and right sub-intervals are merged to complete the sorting of the [left, right) interval sequence

• Simply encapsulate the MergeSort function for external calls:

  void _MergeSort(int* arr, int size)
  {
  	assert(arr);
  	int* tem = (int*)malloc(sizeof(int) * size);
  	assert(tem);
  	MergeSort(arr, tem, 0, size);
      free(tem);
  }
  

• arr is the array to be sorted , size is the number of elements in the array , and MergeSort is a merge sort recursive function

4. Implementation of non-recursive recursive sorting

1. Non-recursive recursive sorting algorithm idea:

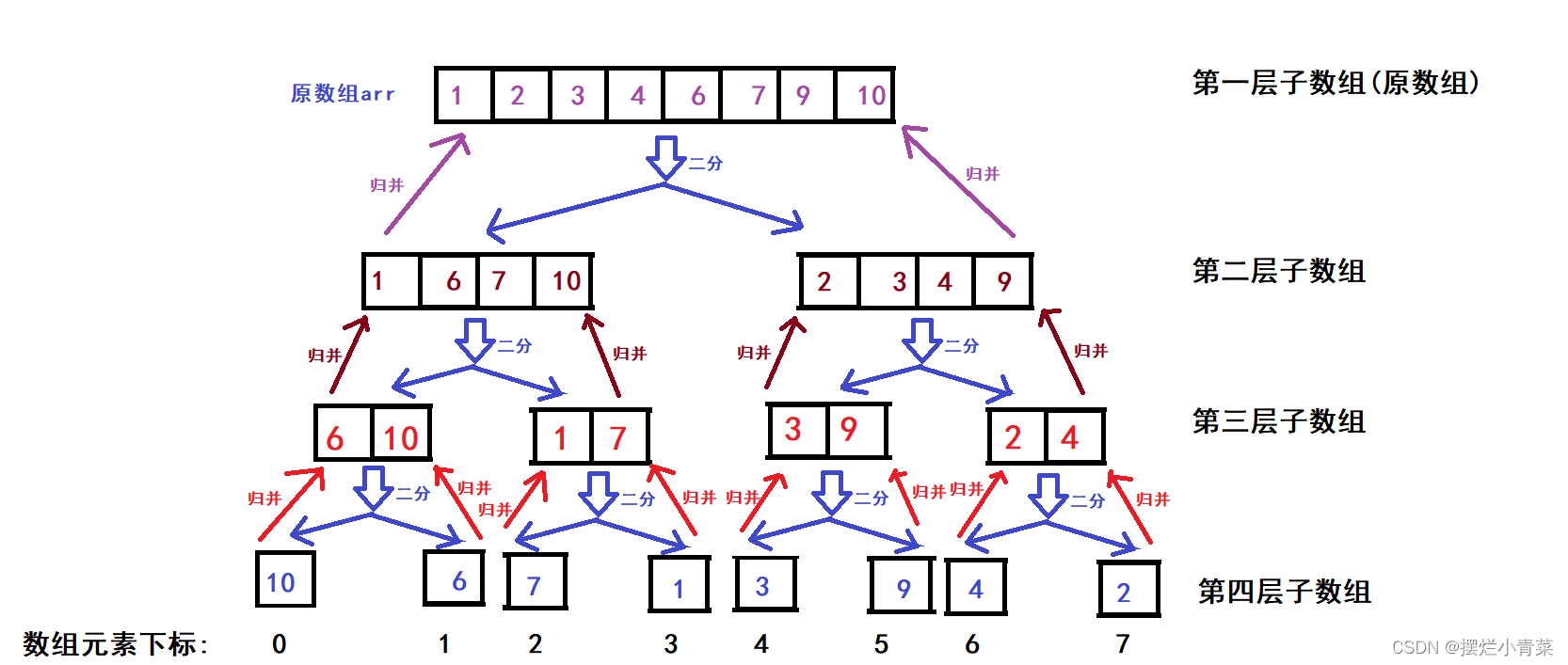
• An illustration of the array being gradually divided into two during the merge sort process :
• The recursive implementation of merge sort uses post-order traversal logic to complete the pairwise merge operation of each sub-array: 
• However, we can also use logic similar to layer order traversal to realize the process of merging sub-arrays in pairs :

Start from the top sub-array to merge the sibling sub-arrays in pairs , complete the merging of the first layer of sub-arrays, continue to complete the merging of the previous layer of sub-arrays, and finally complete the sorting of the original array. We can realize this process by looping

2. Algorithm implementation

• Non-recursive recursion and sort function header:

  void MergeSortNonR(int* arr, int size)

  arr represents the array to be sorted , size is the number of elements of the array to be sorted

• First assume the number of elements of the array being processed : N= (that is, the array can be completely divided into n times )
• Take gap as the number of elements of each sub-array at a certain level of the binary tree structure : the initial value of gap is 1 ( the number of elements in the deepest sub-array is 1 ), and then the gap is incremented by gap=2*gap , and the sorting function is controlled by gap Outermost loop :

  	for (int gap = 1; gap < size; gap *= 2)   //完成logN个层次的子数组的归并
  	{
  
  	}

  This loop can be performed log(size) times, and for each gap value, a pairwise merging of sub-arrays of a level is completed :

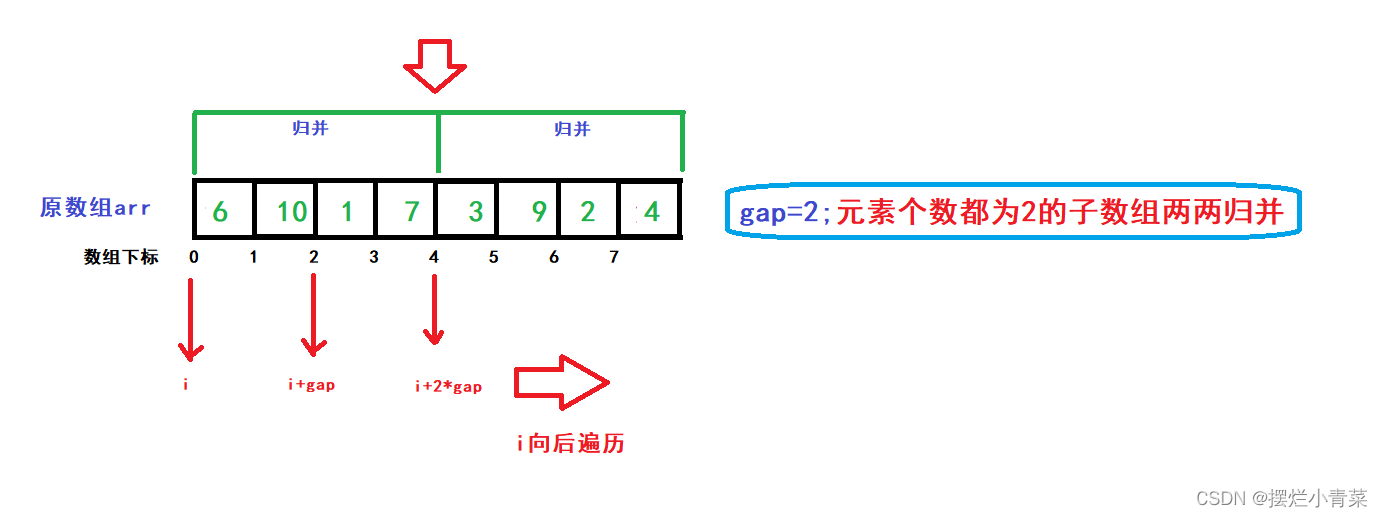
• Then use a variable i to traverse each merged sequence group in each gap situation (each sequence group consists of two sub-arrays ):

   

  	for (int gap = 1; gap < size; gap *= 2)      //完成logN个层次的子数组的归并
  	{
  		for (int i = 0; i < size; i += 2 * gap)  //i每次跳过一个归并序列组(每个序列组有两个子数组)
  		{
  			//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作
  		}
  	}

   Illustration:

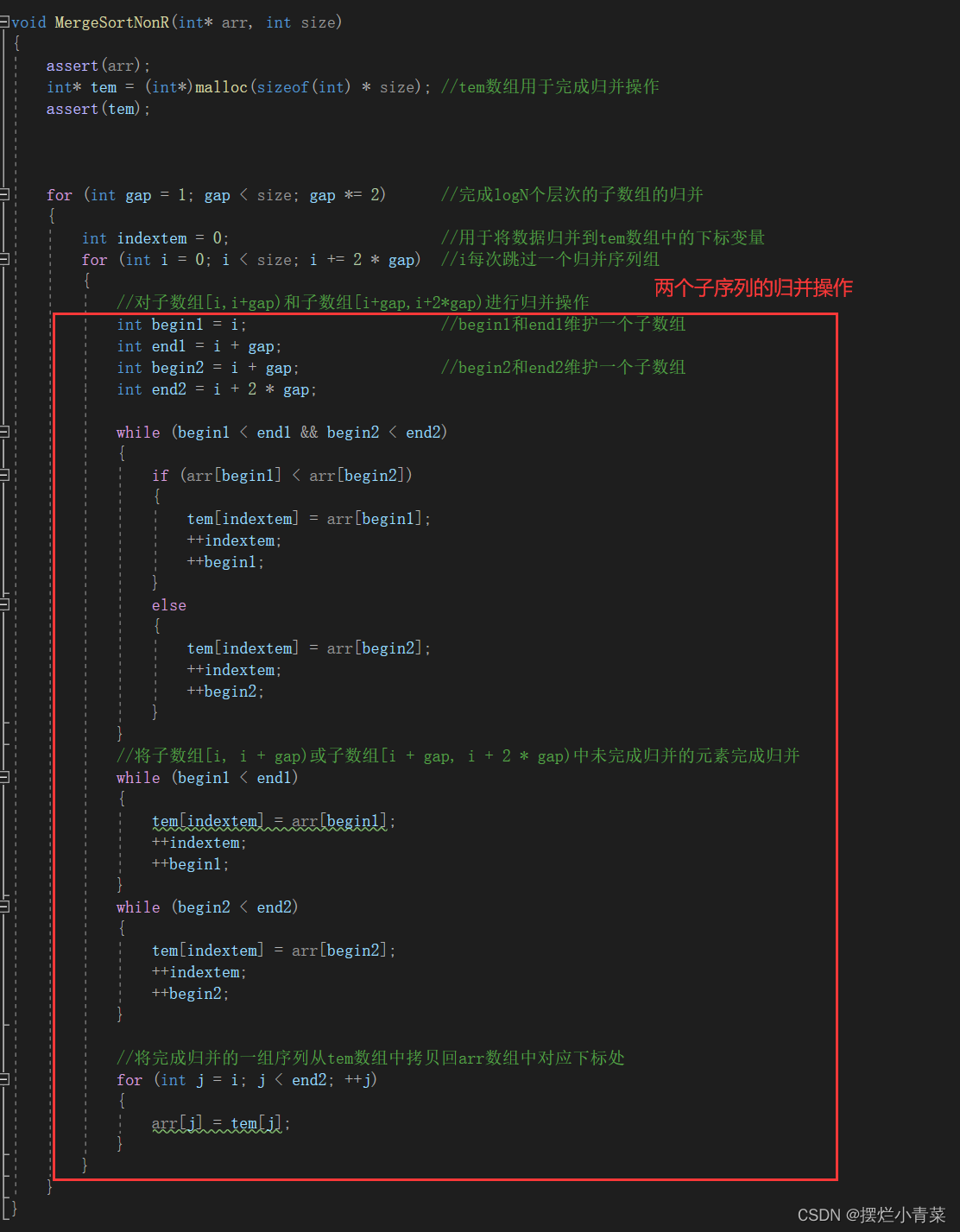
• Preliminary non-recursive merge sort function:

  void MergeSortNonR(int* arr, int size)
  {
  	assert(arr);
  	int* tem = (int*)malloc(sizeof(int) * size); //tem数组用于完成归并操作
  	assert(tem);
  
  	
  
  	for (int gap = 1; gap < size; gap *= 2)      //完成logN个层次的子数组的归并
  	{
  		int indextem = 0;						 //用于将数据归并到tem数组中的下标变量
  		for (int i = 0; i < size; i += 2 * gap)  //i每次跳过一个归并序列组(每个序列组有两个子数组)
  		{
  			//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作
  			int begin1 = i;                      //begin1和end1维护一个子数组
  			int end1 = i + gap; 
  			int begin2 = i + gap;				 //begin2和end2维护一个子数组
  			int end2 = i + 2 * gap;
  
  			while (begin1 < end1 && begin2 < end2)
  			{
  				if (arr[begin1] < arr[begin2])
  				{
  					tem[indextem] = arr[begin1];
  					++indextem;
  					++begin1;
  				}
  				else
  				{
  					tem[indextem] = arr[begin2];
  					++indextem;
  					++begin2;
  				}
  			}
  			//将子数组[i, i + gap)或子数组[i + gap, i + 2 * gap)中未完成归并的元素完成归并
  			while (begin1 < end1)
  			{
  				tem[indextem] = arr[begin1];
  				++indextem;
  				++begin1;
  			}
  			while (begin2 < end2)
  			{
  				tem[indextem] = arr[begin2];
  				++indextem;
  				++begin2;
  			}
  
  			//将完成归并的一组序列从tem数组中拷贝回arr数组中对应下标处
  			for (int j = i; j < end2; ++j)
  			{
  				arr[j] = tem[j];
  			}
  		}
  	}
  
      free(tem);
  }

• 

  For the merge operation of two sub-arrays, see the previous chapter; 

• The preliminary non-recursive recursive sorting function can only handle arrays with elements (that is, the array can be completely divided into n times )

• To enable the sorting function to handle arrays with any number of elements , we must perform algorithmic boundary condition analysis and boundary correction

In general (the number of elements in the sorted array is not ) boundary condition analysis:

• Set the number of elements of the array to be sorted to size
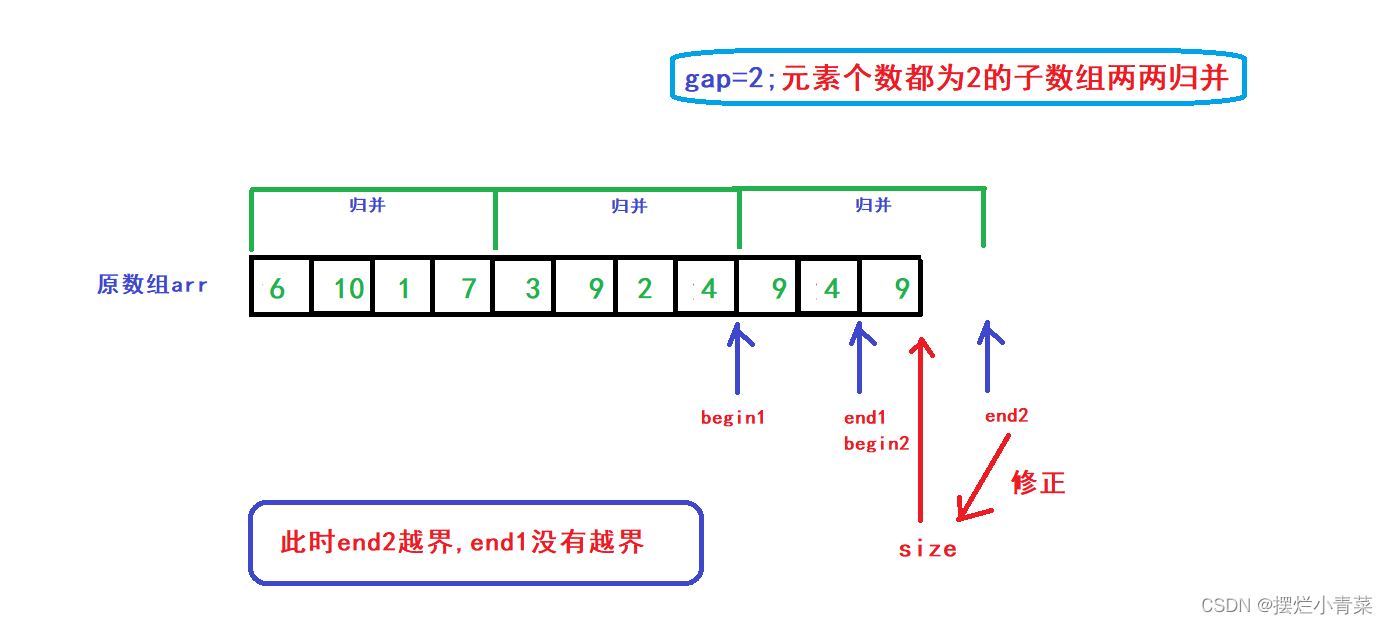
• In the function, only the subscripts end1, begin2, and end2 may cross the boundary ( begin1, end1 , begin2, and end2 in the function are respectively used to maintain two adjacent sub-arrays to be merged in the array arr )

• When the number of array elements being processed is not large , there may be two subscript out-of-bounds situations in the figure below

1. end1 (end1==begin2) is out of bounds (end1>size) ( end2 must also be out of bounds at this time ) At this time, you can directly break to terminate the cycle controlled by i (end1>size means that after the arr array is divided according to the gap , there is only one interval at the end to be merged . Merge operation not required)

2. end2 is out of bounds (end2>size) ( end1 is not out of bounds (end1<size) )

   

   At this point, end2 should be corrected to size , and then the merging operation of the remaining two sub-arrays at the end of the arr array ( after being divided according to the gap ) can be completed:

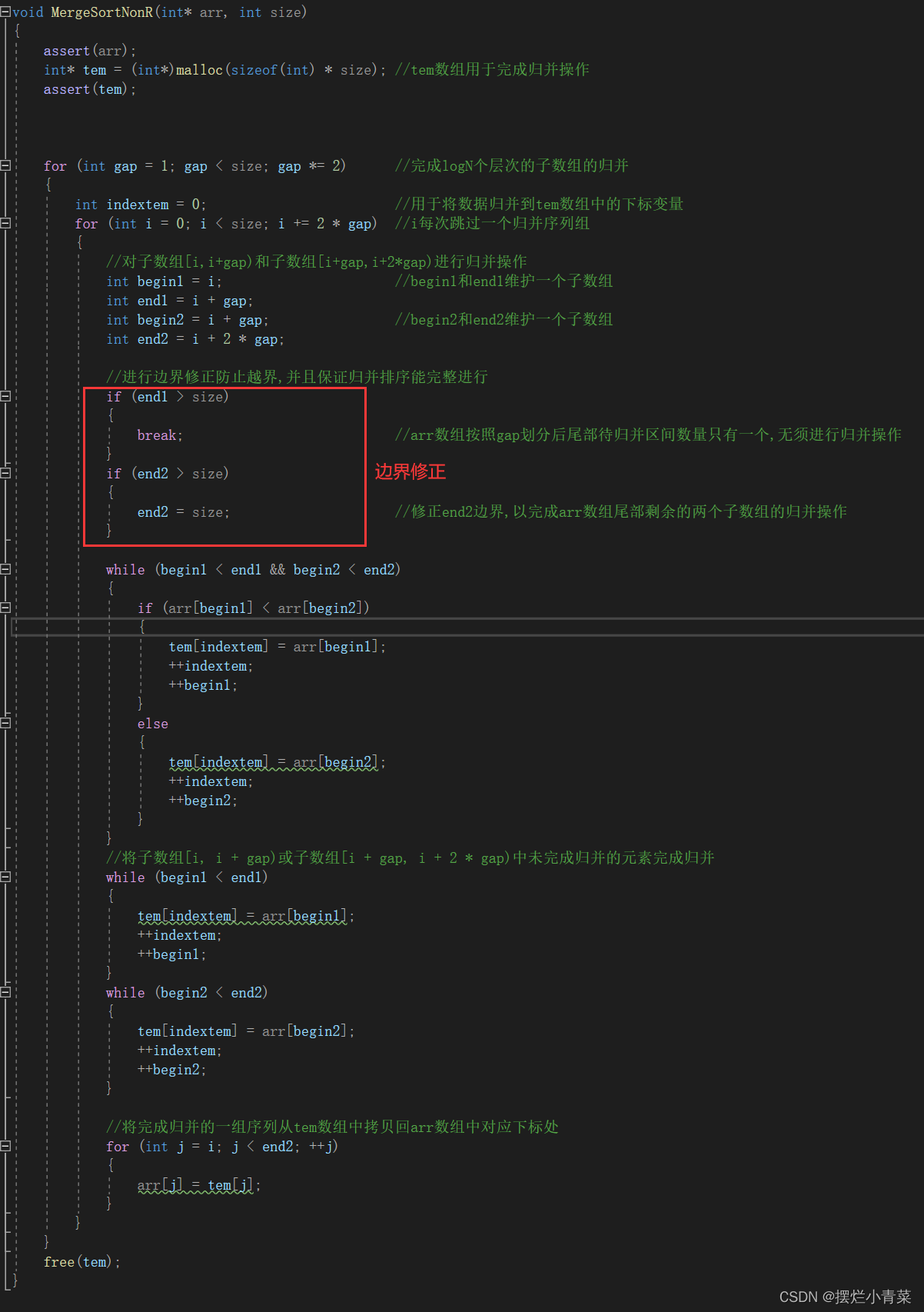
Bounds corrected non-recursive merge sort function

void MergeSortNonR(int* arr, int size)
{
	assert(arr);
	int* tem = (int*)malloc(sizeof(int) * size); //tem数组用于完成归并操作
	assert(tem);

	

	for (int gap = 1; gap < size; gap *= 2)      //完成logN个层次的子数组的归并
	{
		int indextem = 0;						 //用于将数据归并到tem数组中的下标变量
		for (int i = 0; i < size; i += 2 * gap)  //i每次跳过一个归并序列组
		{
			//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作
			int begin1 = i;                      //begin1和end1维护一个子数组
			int end1 = i + gap; 
			int begin2 = i + gap;				 //begin2和end2维护一个子数组
			int end2 = i + 2 * gap;

			//进行边界修正防止越界,并且保证归并排序能完整进行
			if (end1 > size)
			{
				break;                           //arr数组按照gap划分后尾部待归并区间数量只有一个,无须进行归并操作
			}
			if (end2 > size)
			{
				end2 = size;                     //修正end2边界,以完成arr数组尾部剩余的两个子数组的归并操作
			}
			
			while (begin1 < end1 && begin2 < end2)
			{
				if (arr[begin1] < arr[begin2])
				{
					tem[indextem] = arr[begin1];
					++indextem;
					++begin1;
				}
				else
				{
					tem[indextem] = arr[begin2];
					++indextem;
					++begin2;
				}
			}
			//将子数组[i, i + gap)或子数组[i + gap, i + 2 * gap)中未完成归并的元素完成归并
			while (begin1 < end1)
			{
				tem[indextem] = arr[begin1];
				++indextem;
				++begin1;
			}
			while (begin2 < end2)
			{
				tem[indextem] = arr[begin2];
				++indextem;
				++begin2;
			}

			//将完成归并的一组序列从tem数组中拷贝回arr数组中对应下标处
			for (int j = i; j < end2; ++j)
			{
				arr[j] = tem[j];
			}
		}
	}
	free(tem);
}

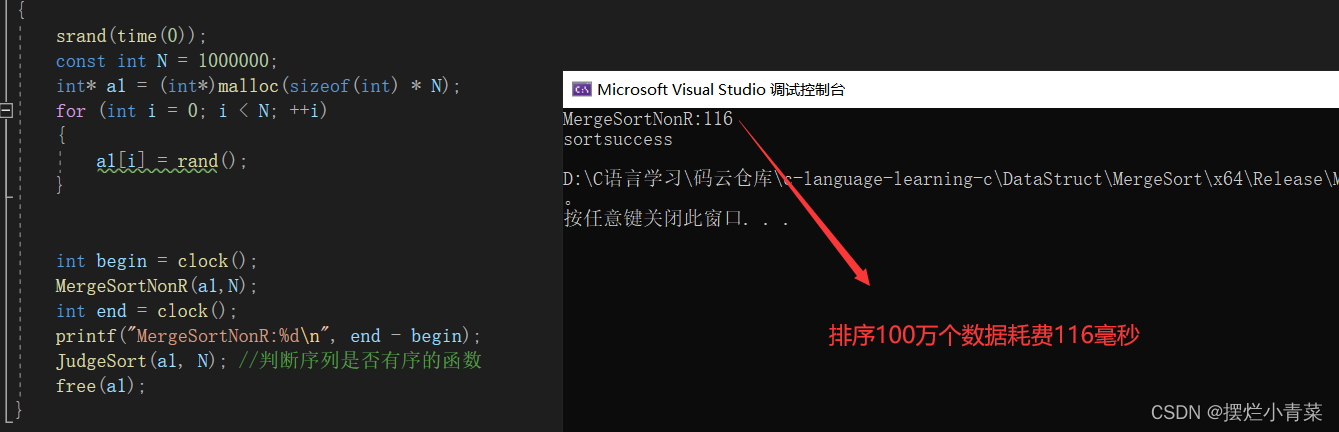
Sorting test:

int main()
{
    //排序100万个数据
    srand(time(0));
	const int N = 1000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
	}

	int begin = clock();
	MergeSortNonR(a1,N);
	int end = clock();
	printf("MergeSortNonR:%d\n", end - begin);
	JudgeSort(a1, N); //判断序列是否有序的函数
	free(a1);
}

• Non-recursive recursive sorting and recursive recursive sorting have no difference in algorithmic thinking (only the order of sub-array merging is different) . The time complexity of both is O(NlogN), and the space complexity is O(N) (in the algorithm It is necessary to open up an additional array tem to complete the pairwise merge operation of subsequences ), but recursive recursion and sorting have additional system stack overhead .