LeetCode's dynamic programming 2 different paths (62), different paths II (63), minimum path and (64)

1. Different paths (62)

Title description:

[Medium]
A robot is located in the upper left corner of an mxn grid (the starting point is marked as "Start" in the figure below).

The robot can only move one step down or to the right at a time. The robot tries to reach the bottom right corner of the grid (labeled "Finish" in the image below).

How many different paths are there in total?
Example:

输入：m = 3, n = 7
输出：28

Topic link

Thinking analysis

1. Since we can only move one step down or to the right at each step, if we want to go to (i, j)(i,j), if we go one step down, then we will go from (i-1, j)( i−1,j) come over; if you go one step to the right, you will come over from (i, j-1)(i,j−1).

2. Then it can be decomposed into overlapping sub-problems for solving, using dynamic programming:

Step 1: Define the status

dp[i][j]: Indicates the total number of paths starting from the upper left corner to the position (i, j)

Step 2: State transition equation

dp[i][j] = dp[i-1][j] + dp[i][j-1]

• dp[i-1][j] represents the number of paths from above.
• dp[i][j-1] represents the number of paths from the left.

Step 3: Initial values ​​(boundary conditions)

• For the first row dp[0][j], or the first column dp[i][0], since they are all on the boundary, it can only be 1
• dp[0][j]==1;dp[i][0]==1

Step 4: Reflection output, return value

• Returns the value of the lower right corner of the dp matrix, that is, the total number of different paths to the end point

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp=[[0]*n for _ in range(m)]
        # 初始化
        for i in range(m):
            dp[i][0]=1
        for j in range(n):
            dp[0][j]=1
        # 转移方程，进行填充
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[-1][-1]

• Time complexity: $O\left(mn\right)$
• Space complexity: $O\left(mn\right)$

Step 5: Thinking about state compression

• Because we only need dp[i-1][j],dp[i][j-1] each time, we only need to record these two numbers.

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        cur = [1] * n
        for i in range(1, m):
            for j in range(1, n):
                cur[j] += cur[j-1]
        return cur[-1]

• Time complexity: $O\left(mn\right)$
• Space complexity: $O\left(n\right)$

2. Different paths II (63)

Title description:

[Medium]
A robot is located in the upper left corner of an mxn grid (the starting point is marked as "Start" in the figure below).

The robot can only move one step down or to the right at a time. The robot tries to reach the bottom right corner of the grid (labeled "Finish" in the image below).

Now consider that there are obstacles in the grid. So how many different paths will there be from the upper left corner to the lower right corner?

Obstacles and empty positions in the grid are represented by 1 and 0 respectively.
Example 1:

 输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

Topic link

Thinking analysis

3. The minimum path sum (64)

Title description:

【medium】

Given an mxn grid containing non-negative integers, please find a path from the upper left corner to the lower right corner so that the sum of the numbers on the path is the smallest.

Note: You can only move one step down or right at a time.

Example one

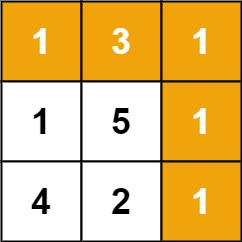
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

prompt:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

Topic link

Thinking analysis

1. Since the direction of the path can only be down or right, each element in the first row of the grid can only move from the upper left corner element to the right, and each element in the first column of the grid can only Starting from the upper left corner element and moving down to arrive, the path at this time is unique, so the minimum path sum corresponding to each element is the sum of the numbers on the corresponding path.

2. For elements that are not in the first row and first column, you can move one step down from the adjacent element above it, or move one step to the right from the adjacent element on the left, and the minimum path corresponding to the element is equal to the adjacent element above it. The minimum path sum corresponding to the element and its left adjacent element plus the minimum value of the current element. Since the minimum path corresponding to each element is related to the minimum path sum corresponding to its neighboring elements, dynamic programming can be used to solve the problem.

Step 1: Define the status

dp[i][j]: Represents the minimum path sum from the upper left corner to the position (i, j),易知dp[0][0]=grid[0][0]

Step 2: State transition equation

• When i=0 and j=0, the upper left corner element of the matrix is ​​also the starting point:dp[0][0]=grid[0][0]
• When i=0 and j>0 is the first row of the matrix:dp[0][j]=dp[0][j-1]+grid[0][j]
• When i>0 and j=0 is the first column of the matrix:dp[i][0]=dp[i-1][0]+grid[i][0]
• When i>0 and j>0 are non-boundary elements of the matrix:dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]

Step 3: Initial values ​​(boundary conditions)

• dp can be initialized

Step 4: Reflection output, return value

• Returns the value of the lower right corner of the dp matrix, that is, the smallest path to the end and

Step 5: Thinking about state compression

• Since the dp matrix has the same dimensions as the original matrix, we can directly modify the original matrix to the minimum path sum of the current position.

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i == j == 0: continue
                elif i == 0:  grid[i][j] = grid[i][j - 1] + grid[i][j]
                elif j == 0:  grid[i][j] = grid[i - 1][j] + grid[i][j]
                else: grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]
        return grid[-1][-1]

• Time complexity: $O\left(mn\right)$ : Traverse the entire matrix
• Space complexity: $O\left(1\right)$ : directly modify the original matrix without using extra space