leetCode 63. Different paths II dynamic programming + space complexity optimization one-dimensional dp

63. Different Paths II - LeetCode

A robot is located in  m x n the upper left corner of a grid (the starting point is marked "Start" in the image below).

The robot can only move one step down or to the right at a time. The robot attempts to reach the lower right corner of the grid (labeled "Finish" in the image below).

Now consider that there are obstacles in the grid. So how many different paths will there be from the upper left corner to the lower right corner?

Obstacles and empty locations in the grid are represented by  1 and  respectively 0 .

Example 1:

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
 Output: 2
 Explanation: There is an obstacle in the middle of the 3x3 grid.2There are a total of three different paths 
from the upper left corner to the lower right corner :
1. Right -> Right -> Down -> Down
2. Down->Down->Right->Right

Example 2:

Input: obstacleGrid = [[0,1],[0,0]]
 Output: 1

>>Ideas

Compared with this leetCode 62. There are obstacles in different paths ~. In fact, when there are obstacles, just mark the corresponding dp array and keep the initial value (0)! ! !

>>Five Steps of Dynamic Rules

1. Determine the meaning of dp array (dp table) and subscripts

dp[i][j]: Indicates that starting from (0,0), there are dp[i][j] different paths to (i,j)

2. Determine the recursion formula

• When there is no obstacle, dp[i][j] = dp[i-1][j] + dp[i][j-1];
• When there is an obstacle, then (i, j) maintains the initial state (the initial state is 0)

if(obstacleGrid[i][j] == 0) { // 当(i,j)没有障碍的时候，再推导dp[i][j]
    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

3.dp array initialization

vector<vector<int>> dp(m,vector<int>(n,0));//初始值为0
for(int i = 0;i < m;i++) dp[i][0] = 1;
for(int j = 0;j < n;j++) dp[0][j] = 1;

• Because there is only one path from the position of (0,0) to (i,0), that is, dp[i][0] must be 1;
• Because there is only one path from the position of (0,0) to (0,j), that is, dp[0][j] must be 1;

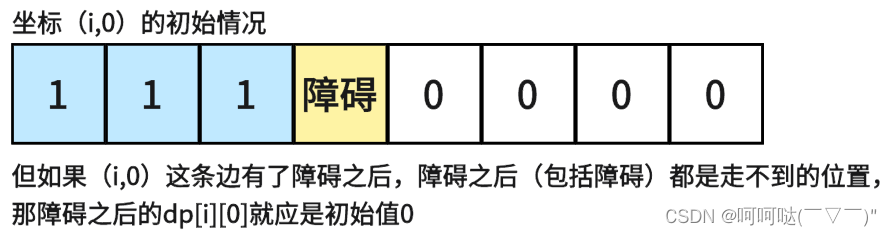
But if there is an obstacle on the edge (i,0), and the position after the obstacle (including the obstacle) is unreachable, then dp[i][0] after the obstacle should be the initial value 0 

vector<vector<int>> dp(m,vector<int>(n,0));//初始值为0
for(int i = 0;i < m && obstacleGrid[i][0] == 0;i++) dp[i][0] = 1;
for(int j = 0;j < n && obstacleGrid[0][j] == 0;j++) dp[0][j] = 1;

Note the termination condition of the for loop:

• ① When obstacleGrid[i][0] == 1 is encountered , the operation of assigning 1 to dp[i][0] is terminated.
• ② When obstacleGrid[0][j] == 1 is encountered , the operation of assigning 1 to dp[0][j] is terminated.

4. Determine the traversal order

It can be seen from the recursive formula dp[i][j] = dp[i-1][j] + dp[i][j-1] that it must be traversed layer by layer from left to right , which can be guaranteed When deriving dp[i][j], dp[i-1][j] and dp[i][j-1] must have numerical values.

for(int i = 1;i < m;i++) {
    for(int j = 1;j < n;j++) {
        if(obstacleGrid[i][j]  == 1) continue;
        dp[i][j] = dp[i-1][j] + dp[i][j-1];
    }
}

5. Derivation of dp array with examples

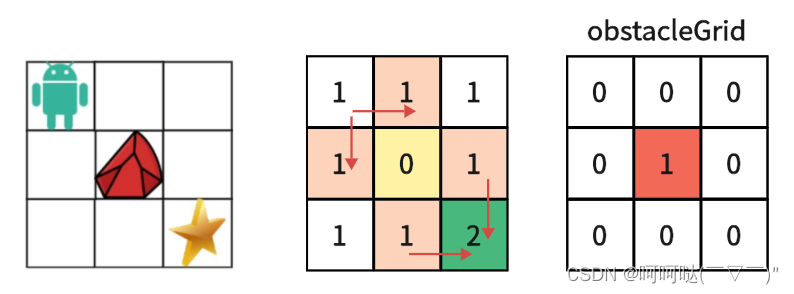
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        if(obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0
            return 0;
        vector<vector<int>> dp(m,vector<int>(n,0));
        for(int i=0;i<m && obstacleGrid[i][0] == 0;i++) dp[i][0] = 1;
        for(int j=0;j<n && obstacleGrid[0][j] == 0;j++) dp[0][j] = 1;
        for(int i=1;i<m;i++) {  
            for(int j=1;j<n;j++) {
                if(obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

// 时间复杂度：O(m x n) m、n分别为 obstacleGrid 的宽度和长度
// 空间复杂度：O(m x n)

• Time complexity: O(mxn) m and n are the width and length of obstacleGrid respectively.
• Space complexity: O(mxn)

Further space optimization:

class Solution {
public:

    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid[0][0] == 1) return 0;
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<int> dp(n);
        for(int j = 0;j < n;j++) {
            if(obstacleGrid[0][j] == 1)
                dp[j] = 0;
            else if(j == 0)
                dp[j] = 1;
            else
                dp[j] = dp[j-1];
        }
        for(int i = 1;i < m;++i) {
            for(int j = 0;j < n;++j) {
                if(obstacleGrid[i][j] == 1) dp[j] = 0;
                else if(j!=0) 
                    dp[j] = dp[j] + dp[j-1];
            }
        }
        return dp.back();
    }
    // 时间复杂度：O(m x n) m、n分别为 obstacleGrid 的宽度和长度
    // 空间复杂度：O(n)
};

• Time complexity: O(mxn) m and n are the width and length of obstacleGrid respectively.
• Space complexity: O(n) 

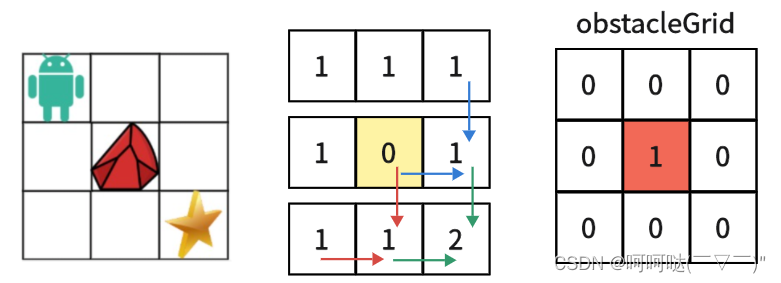
Class screenshots from Code Caprice:

Reference and recommended articles and videos:

Dynamic programming, this time encountered obstacles | LeetCode: 63. Different paths II_bilibili_bilibili

 Code Random Record (programmercarl.com)

My previous articles:  leetCode 62. Dynamic programming of different paths + space complexity optimization_Heheda(￣▽￣)"'s blog-CSDN blog