动量梯度下降(Momentum、指数加权平均)、逐参数适应学习率方法(Adagrad、RMSprop、Adam)、学习率退火、归一化/标准化

日萌社

人工智能AI：Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战（不定时更新）

---

3.1.3 优化算法

这里我们会介绍三种类型的优化算法，不过很多原理都大同小异。

• 1、动量更新方法
• 2、逐参数适应学习率方法
• 3、二阶方法

3.1.3.1 动量梯度下降（Gradient Descent with Momentum）

• 目的：解决因鞍点问题带来的梯度更新停止问题。
• 解决办法：
  • 在随机梯度下降（SGD）中加入指数加权平均数来更新参数的梯度

1、指数加权平均

指数加权平均（Exponentially Weight Average）是一种常用的序列数据处理方式，通常用在序列场景如金融序列分析、温度变化序列分析。

假设给定一个序列，例如北京一年每天的气温值，图中蓝色的点代表真实数据。

那么这样的气温值变化可以理解成优化的过程波动较大，异常较多。那么怎么平缓一些呢，这时候就要用到加权平均值了，如指数加权平均值。首先看一些效果。

使用动量梯度下降时，通过累加过去的梯度值来减少抵达最小值路径上的波动，加速了收敛，因此在横轴方向下降得更快，从而得到图中红色或者紫色的曲线。当前后梯度方向一致时，动量梯度下降能够加速学习；而前后梯度方向不一致时，动量梯度下降能够抑制震荡。

3.1.3.2 逐参数适应学习率方法

前面讨论的方法都是对学习率进行全局地操作，并且对所有的参数都是一样的。

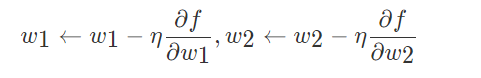
学习率调参是很耗费计算资源的过程，所以很多工作投入到发明能够适应性地对学习率调参的方法，甚至是逐个参数适应学习率调参。很多这些方法依然需要其他的超参数设置，但是其观点是这些方法对于更广范围的超参数比原始的学习率方法有更良好的表现。

• 对不同的参数，每个参数更新的学习率会自适应本身参数特点进行梯度更新
• Adagrad
• RMSprop
• Adam

1、Adagrad

• 理解：
  • 小批量随机梯度按元素平方的累加变量st出现在学习率的分母项中。
  • 1、如果目标函数有关自变量中某个参数的偏导数一直都较大，那么该参数的学习率将下降较快；
  • 2、反之，如果目标函数有关自变量中某个参数的偏导数一直都较小，那么该参数的学习率将下降较慢。
  • 然而，由于st一直在累加按元素平方的梯度，自变量中每个元素的学习率在迭代过程中一直在降低（或不变）。所以，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。

2、RMSProp 算法

刚才当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。为了解决这一问题，RMSProp算法对AdaGrad算法做了一点小小的修改。

不同于AdaGrad算法里状态变量st是截至时间步t所有小批量随机梯度gt按元素平方和，RMSProp（Root Mean Square Prop）算法将这些梯度按元素平方做指数加权移动平均

3、Adam算法

Adam 优化算法（Adaptive Moment Estimation，自适应矩估计）将 Momentum 和 RMSProp 算法结合在一起。Adam算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均。

假设用每一个 mini-batch 计算 dW、db，第t次迭代时：

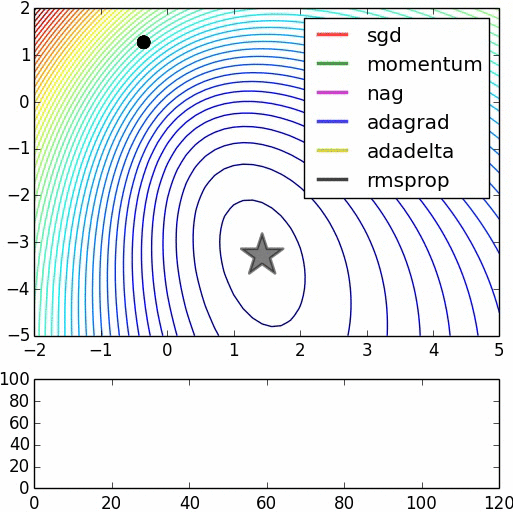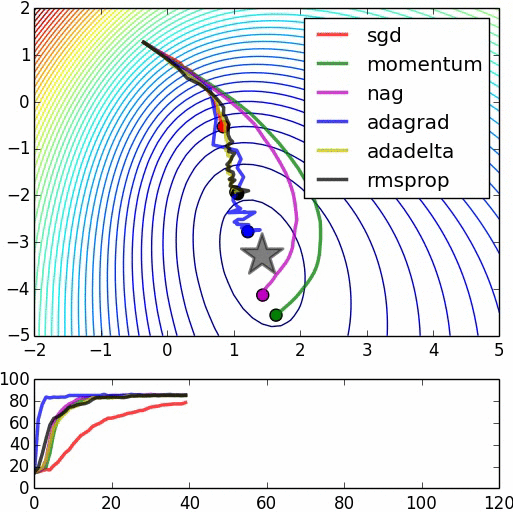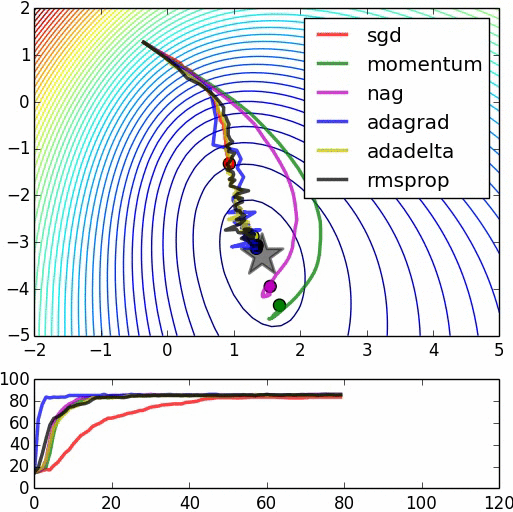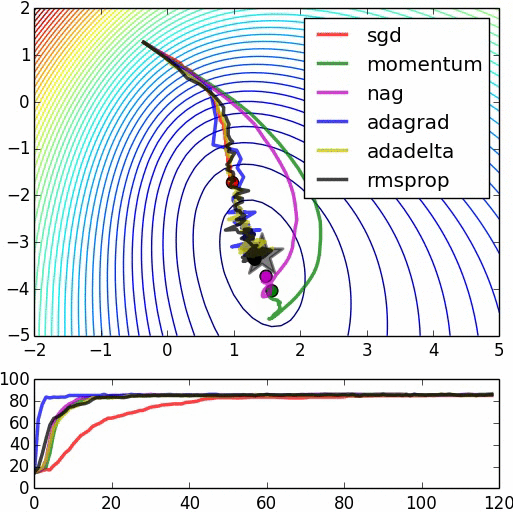
所有优化算法效果对比

• 收敛对比

• 鞍点对比

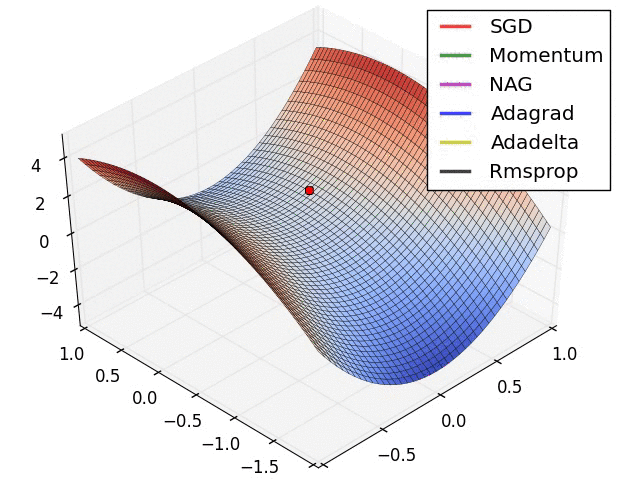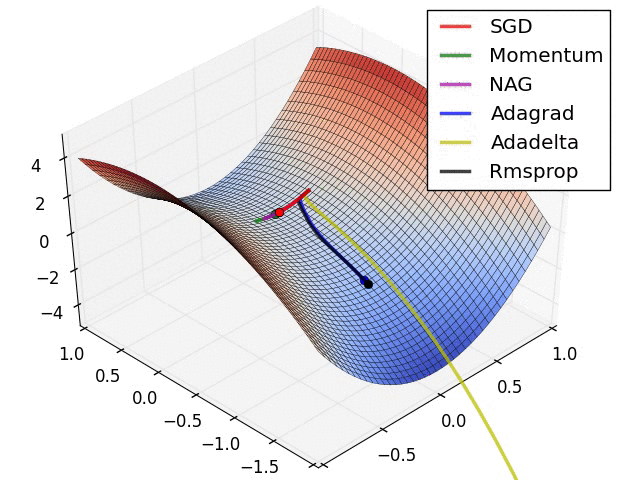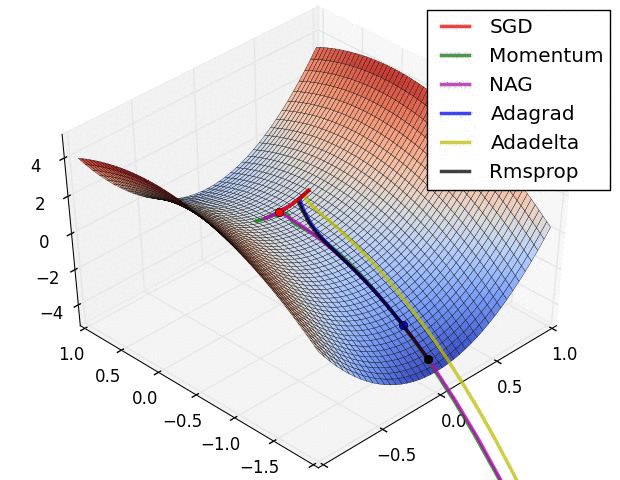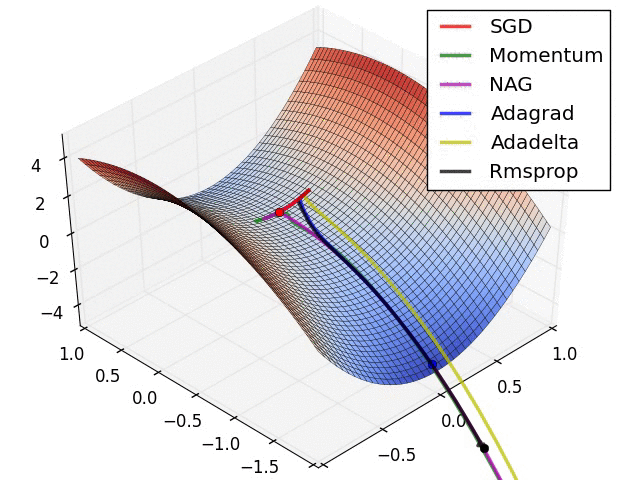
资料来自：Alec Radford做的实验对比

3.1.7 学习率退火

如果设置一个固定的学习率 α

• 在最小值点附近，由于不同的 batch 中存在一定的噪声，因此不会精确收敛，而是始终在最小值周围一个较大的范围内波动。
• 如果随着时间慢慢减少学习率 α 的大小，在初期 α 较大时，下降的步长较大，能以较快的速度进行梯度下降；而后期逐步减小 α 的值，即减小步长，有助于算法的收敛，更容易接近最优解。

最常用的学习率退火方法：

• 1、随步数衰减
• 2、指数衰减

3.1.8 参数初始化策略与归一化输入

3.1.8.1 参数初始化

3.1.8.2 归一化输入

 

3.1.9 案例：动量梯度下降与Adam优化算法实现

1、目的

对以下模型进行优化，分别实现动量和Adam进行对比

# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
z1 = np.dot(W1, X) + b1
a1 = relu(z1)
z2 = np.dot(W2, a1) + b2
a2 = relu(z2)
z3 = np.dot(W3, a2) + b3
a3 = sigmoid(z3)

数据为 train_X, train_Y = sklearn.datasets.make_moons(n_samples=300, noise=.2)创建的简单样本的二分类问题。

2、步骤分析

• 1、数据读取、模型前向与反向传播代码封装
• 2、动量梯度和Adam优化算法的实现

3、代码实现

目录结构为optimization和utils，其中utils为封装好的相关函数（如relu，前向、反向传播函数）这些不需要大家再去实现，前面已经讲解过，optimization中有主要训练逻辑，其中需要大家去进行实现两个优化算法。

2、动量梯度和Adam优化算法的接口实现

utils.py

import numpy as np
import sklearn
import sklearn.datasets


def sigmoid(x):
    """sigmoid函数
    """
    s = 1/(1+np.exp(-x))
    return s


def relu(x):
    """relu函数
    """
    s = np.maximum(0,x)
    
    return s


def initialize_parameters(layer_dims):
    """初始化模型参数函数
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims)

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * np.sqrt(2 / layer_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
        
    return parameters


def compute_cost(a3, Y):
    
    """损失计算函数
    """
    m = Y.shape[1]
    
    logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
    cost = 1./m * np.sum(logprobs)
    
    return cost


def forward_propagation(X, parameters):
    """前向传播模型
    """
    
    # 获取参数
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    z1 = np.dot(W1, X) + b1
    a1 = relu(z1)
    z2 = np.dot(W2, a1) + b2
    a2 = relu(z2)
    z3 = np.dot(W3, a2) + b3
    a3 = sigmoid(z3)
    
    cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)
    
    return a3, cache


def backward_propagation(X, Y, cache):
    """反向传播计算
    """
    m = X.shape[1]
    (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cache
    
    dz3 = 1./m * (a3 - Y)
    dW3 = np.dot(dz3, a2.T)
    db3 = np.sum(dz3, axis=1, keepdims = True)
    
    da2 = np.dot(W3.T, dz3)
    dz2 = np.multiply(da2, np.int64(a2 > 0))
    dW2 = np.dot(dz2, a1.T)
    db2 = np.sum(dz2, axis=1, keepdims = True)
    
    da1 = np.dot(W2.T, dz2)
    dz1 = np.multiply(da1, np.int64(a1 > 0))
    dW1 = np.dot(dz1, X.T)
    db1 = np.sum(dz1, axis=1, keepdims = True)
    
    gradients = {"dz3": dz3, "dW3": dW3, "db3": db3,
                 "da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,
                 "da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}
    
    return gradients


def predict(X, y, parameters):
    """预测函数
    """
    
    m = X.shape[1]
    p = np.zeros((1,m), dtype = np.int)
    
    # 前向计算
    a3, caches = forward_propagation(X, parameters)
    
    # 进行概率0、1转换
    for i in range(0, a3.shape[1]):
        if a3[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0

    print("Accuracy: "  + str(np.mean((p[0,:] == y[0,:]))))
    
    return p


def load_dataset():
    np.random.seed(3)
    train_X, train_Y = sklearn.datasets.make_moons(n_samples=300, noise=.2)
    train_X = train_X.T
    train_Y = train_Y.reshape((1, train_Y.shape[0]))
    return train_X, train_Y

optimization.py

import numpy as np
import math
import sklearn
import sklearn.datasets

from utils import initialize_parameters, forward_propagation, compute_cost, backward_propagation
from utils import load_dataset, predict


def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
    """
    创建每批次固定数量特征值和目标值
    """

    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []

    # 对所有数据进行打乱
    permutation = list(np.random.permutation(m))

    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1, m))

    # 循环将每批次数据按照固定格式装进列表当中
    num_complete_minibatches = math.floor(
        m / mini_batch_size)

    # 所有训练数据分成多少组
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    # 最后剩下的样本数量mini-batch < mini_batch_size
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size:]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches


def initialize_momentum(parameters):
    """
    初始化网络中每一层的动量梯度下降的指数加权平均结果参数
    parameters['W' + str(l)] = Wl
    parameters['b' + str(l)] = bl
    return:
    v['dW' + str(l)] = velocity（速度） of dWl
    v['db' + str(l)] = velocity（速度） of dbl
    """
    # 1、得到网络层数
    L = len(parameters) // 2
    v = {}

    # 2、循环每一层去初始化出动量当前更新梯度(历史的梯度加权和)
    for l in range(L):
        v['dW' + str(l + 1)] = np.zeros(parameters["W" + str(l + 1)].shape)
        v['db' + str(l + 1)] = np.zeros(parameters["b" + str(l + 1)].shape)

    return v


def update_parameters_with_momentum(parameters, gradients, v, beta, learning_rate):
    """
    动量梯度下降算法实现
    """
    L = len(parameters) // 2
    # 根据动量梯度计算公式去得到动量梯度参数更新
    for l in range(L):

        # 1、计算加权结果
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * (gradients["dW" + str(l + 1)])
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * (gradients["db" + str(l + 1)])

        # 2、梯度更新
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]

    return parameters, v


def initialize_adam(parameters):
    """
    初始化Adam算法中的参数
    """
    # 1、网络层数
    L = len(parameters) // 2
    v = {}
    s = {}

    # 2、循环层数迭代初始化一个加权结果参数
    for l in range(L):
        # v初始化
        v["dW" + str(l + 1)] = np.zeros(parameters["W" + str(l + 1)].shape)
        v["db" + str(l + 1)] = np.zeros(parameters["b" + str(l + 1)].shape)

        # s初始化
        s["dW" + str(l + 1)] = np.zeros(parameters["W" + str(l + 1)].shape)
        s["db" + str(l + 1)] = np.zeros(parameters["b" + str(l + 1)].shape)

    return v, s


def update_parameters_with_adam(parameters, gradients, v, s, t, learning_rate=0.01,
                                beta1=0.9, beta2=0.999, epsilon=1e-8):
    """
    更新Adam算法网络的参数
    """
    # 1、得到网络大小层数
    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}

    # 2、更新adam的当中的加权结果，修正结果，梯度更新结果
    for l in range(L):
        # 1、对v计算
        # 对梯度进行移动平均计算。 输入：v, gradients, beta1， 输出：v
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * gradients["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * gradients["db" + str(l + 1)]

        # 进行修正计算
        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1, t))
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1, t))

        # 2、对s计算
        # 对平方梯度移动平均值，输入：s, gradients, beta2， 输出：s
        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.power(gradients["dW" + str(l + 1)], 2)
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.power(gradients["db" + str(l + 1)], 2)

        # 进行修正计算
        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2, t))
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2, t))

        # 3、梯度更新结果计算
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * \
                                       v_corrected["dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon)
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * \
                                       v_corrected["db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon)
    return parameters, v, s


def model(X, Y, layers_dims, optimizer, learning_rate=0.0007, mini_batch_size=64, beta=0.9,
          beta1=0.9, beta2=0.999, epsilon=1e-8, num_epochs=10000, print_cost=True):
    """
    模型逻辑
    """
    # 1、计算网络的层数
    L = len(layers_dims)
    costs = []
    t = 0
    seed = 10

    # 2、初始化网络结构
    parameters = initialize_parameters(layers_dims)

    # 初始化优化器参数
    if optimizer == "momentum":
        v = initialize_momentum(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)

    # 3、优化过程
    for i in range(num_epochs):

        # 每次迭代所有样本顺序打乱不一样
        seed = seed + 1
        # 获取每批次数据
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)

        for minibatch in minibatches:

            # 获取批次的特征数据
            (minibatch_X, minibatch_y) = minibatch

            # 1、前向传播
            a3, cache = forward_propagation(minibatch_X, parameters)

            # 2、计算损失
            cost = compute_cost(a3, minibatch_y)

            # 3、反向传播计算梯度
            gradients = backward_propagation(minibatch_X, minibatch_y, cache)

            # 4、选择优化算法进行梯度更新
            if optimizer == "momentum":

                parameters, v = update_parameters_with_momentum(parameters, gradients, v, beta, learning_rate)

            elif optimizer == "adam":
                t = t + 1
                parameters, v, s = update_parameters_with_adam(parameters, gradients, v, s, t, learning_rate, beta1, beta2, epsilon)

        # 每个1000批次打印损失
        if print_cost and i % 1000 == 0:
            print("第 %i 次迭代的损失值: %f" % (i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)

    return parameters, costs


if __name__ == '__main__':

    train_X, train_Y = load_dataset()
    print(train_X, train_Y)

    layers_dims = [train_X.shape[0], 5, 2, 1]

    parameters, costs = model(train_X, train_Y, layers_dims, optimizer="adam")

    predictions = predict(train_X, train_Y, parameters)

    parameters, costs = model(train_X, train_Y, layers_dims, optimizer="momentum")

    predictions = predict(train_X, train_Y, parameters)

• 运行效果如下

# adam算法优化效果
第 0 次迭代的损失值: 0.690552
第 1000 次迭代的损失值: 0.185501
第 2000 次迭代的损失值: 0.150830
第 3000 次迭代的损失值: 0.074454
第 4000 次迭代的损失值: 0.125959
第 5000 次迭代的损失值: 0.104344
第 6000 次迭代的损失值: 0.100676
第 7000 次迭代的损失值: 0.031652
第 8000 次迭代的损失值: 0.111973
第 9000 次迭代的损失值: 0.197940
Accuracy: 0.94

# momentum算法优化效果
第 0 次迭代的损失值: 0.690741
第 1000 次迭代的损失值: 0.685341
第 2000 次迭代的损失值: 0.647145
第 3000 次迭代的损失值: 0.619594
第 4000 次迭代的损失值: 0.576665
第 5000 次迭代的损失值: 0.607324
第 6000 次迭代的损失值: 0.529476
第 7000 次迭代的损失值: 0.460936
第 8000 次迭代的损失值: 0.465780
第 9000 次迭代的损失值: 0.464740
Accuracy: 0.7966666666666666

3.1.10 总结

• 局部最优问题、鞍点与海森矩阵
• 批梯度下降算法的优化
• 三种类型的优化算法
• 学习率退火策略
• 参数初始化策略与输入归一化策略

---

局部最优与梯度消失爆炸问题

---

Adam与SGD对比