【多传感融合】优达学城多传感融合学习笔记（三）——将激光雷达3D点云映射到相机图像（上）

将激光雷达3D点云映射到相机图像（上）——原理分析

齐次坐标系

为了将激光雷达3D点云映射到相机二维图像上，我们可以使用本系列教程的第一篇针孔相机模型中得到的如下投影公式：

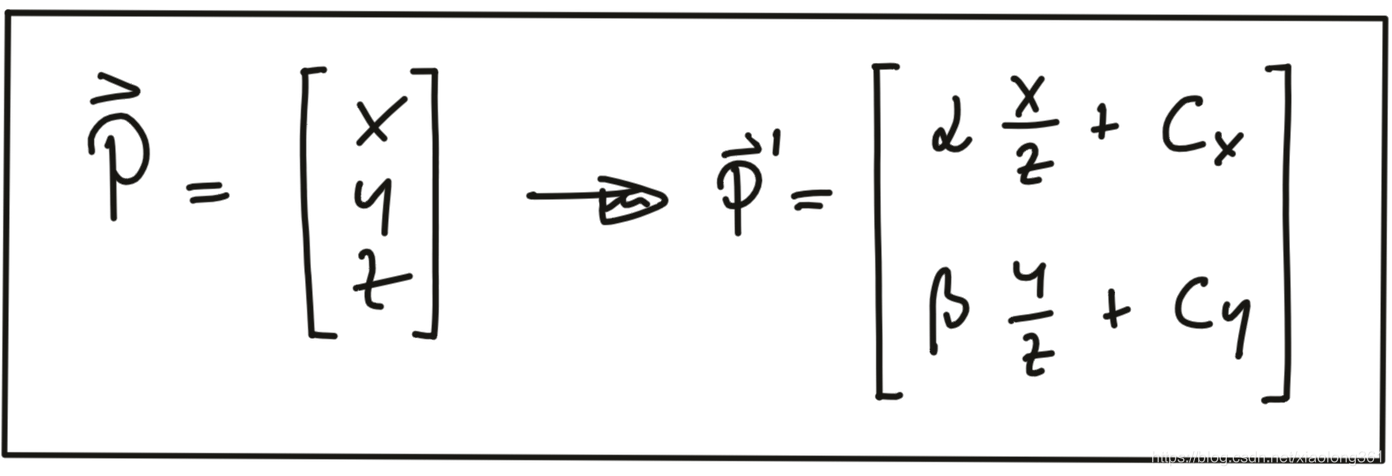
除了构成投影几何关系的摄像机自身参数外，我们还需要知道关于摄像机和激光雷达在公共参考坐标系中的相对位置关系。从激光雷达到相机需要经过平移和旋转坐标系转换操作，我们需要将这些转换操作应用到每个3D点上。因此，我们的目标是简化用来表示映射的符号。通过使用线性变换，3D点可以用向量来表示，其平移、旋转、缩放和透视投影等操作可以用与向量相乘的矩阵表示。有了上述方法，到目前为止，我们要得到的投影方程仅剩的问题是它们涉及到关于 $Z$的除法，这使得它们变得非线性的，从而影响了我们把它们转换成更加方便的矩阵向量形式。

避免这个问题的一种方法就是改变坐标系，从最初的欧几里得坐标系变成齐次坐标系。在这两个坐标系之间来回切换的是一个非线性的操作，但是一旦我们身处齐次坐标系中，像上面给出的投影变换关系就会变成线性的，这样便可以用简单的矩阵-向量乘法来表示。两种坐标系之间的转换如下图所示。

在 $n$维欧几里德坐标系中，一个点可以由一个 $n$维向量表示。通过简单地将数字 $1$作为一个额外的分量就可以将其转换成 $(n+1)$维齐次坐标。该变换既可以应用于图像坐标，也可以应用于场景坐标。

要将齐次坐标转换回欧几里得坐标系，只需要去掉向量中最后一个维度坐标，并用前 $n$个坐标除以去掉的最后一个维度坐标，如上图所示。如前所述，这是一个非线性操作，一旦我们回到欧几里德空间，就会失去将不同参数精确地分离成单独的矩阵分量（即线性化表示坐标系映射关系）的能力。接下来，我们将研究这些矩阵分量。

内参（Intrinsic Parameters）

下面我们将用矩阵-向量的形式来表示投影方程：

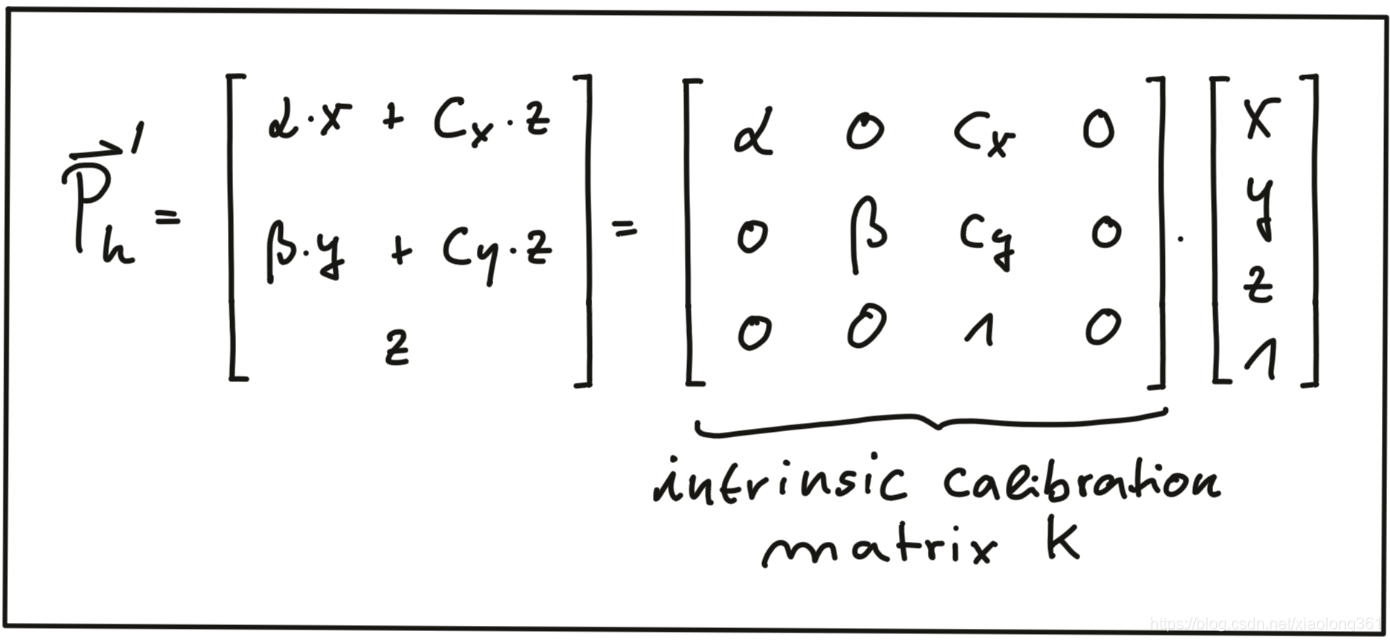
可以看出，相机的**内在参数（Intrinsic Parameters，简称内参）**被提取到一个矩阵中，这样可以用一种非常简洁的方式表示我们的针孔相机模型的一般属性。更加复杂的相机模型属性，如歪斜（skewness）或剪切（shear），也可以很容易地添加。

下面网站中提供的视频动画形象地展示了相机的各个内参对图像平面上物体外观显示的影响：http://ksimek.github.io/2013/08/13/intrinsic/，该网站中的视频动画示意图如下图所示。

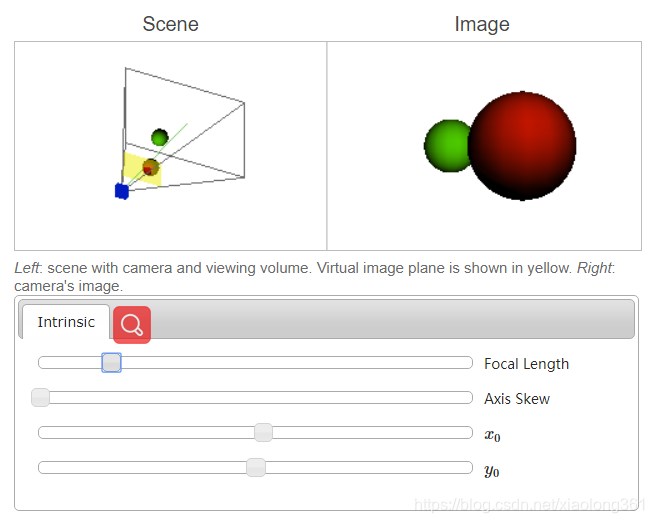
外参（Extrinsic Parameters）

在以针孔为中心的相机坐标系中，三维空间中的点 $P$与二维图像平面中的点 $P'$之间的映射关系已经被描述出来了。但是，如果我们在三维空间中拥有的关于点的信息都是在另一个坐标系中，例如在许多汽车应用程序中常见的汽车坐标系，那么情况又该如何呢?如下图所示，车辆坐标系原点位于车辆后轴中点下方的地面上，x轴指向行驶方向。除了坐标轴命名约定外，下图中还显示了绕X、Y和Z轴旋转时通常使用的角度名称，即“roll”、“pitch”和“yaw”。

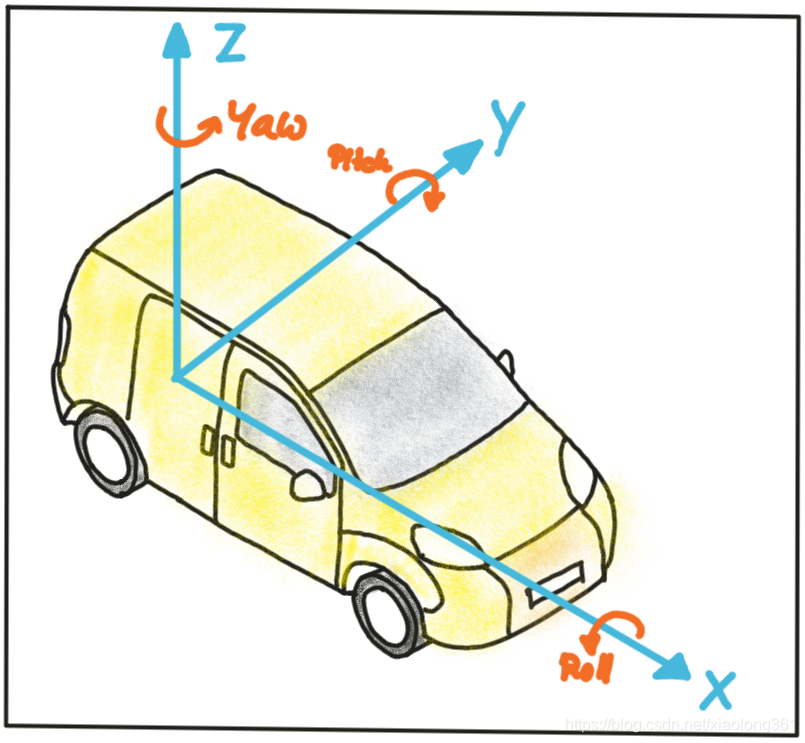
我们假设该车配备了激光雷达和相机，它们都将在车辆坐标系下进行坐标校准。为了将在激光雷达坐标系中测量到的点投射到相机坐标系中，我们需要在映射操作中添加一个额外的转换，使我们能够将点从车辆坐标系关联到相机坐标系，反之亦然。通常，这种映射操作可以分为三个部分：平移（translation）、旋转（rotation ）和缩放（scaling）。让我们依次对它们进行分析：
平移：由下图可见，平移描述了从点 $\overrightarrow{P}$到新位置 $\overrightarrow{P^{'}}$的线性移动，该移动可以通过给 $\overrightarrow{P^{}}$
加上一个平移向量 $\overrightarrow{t}$实现。

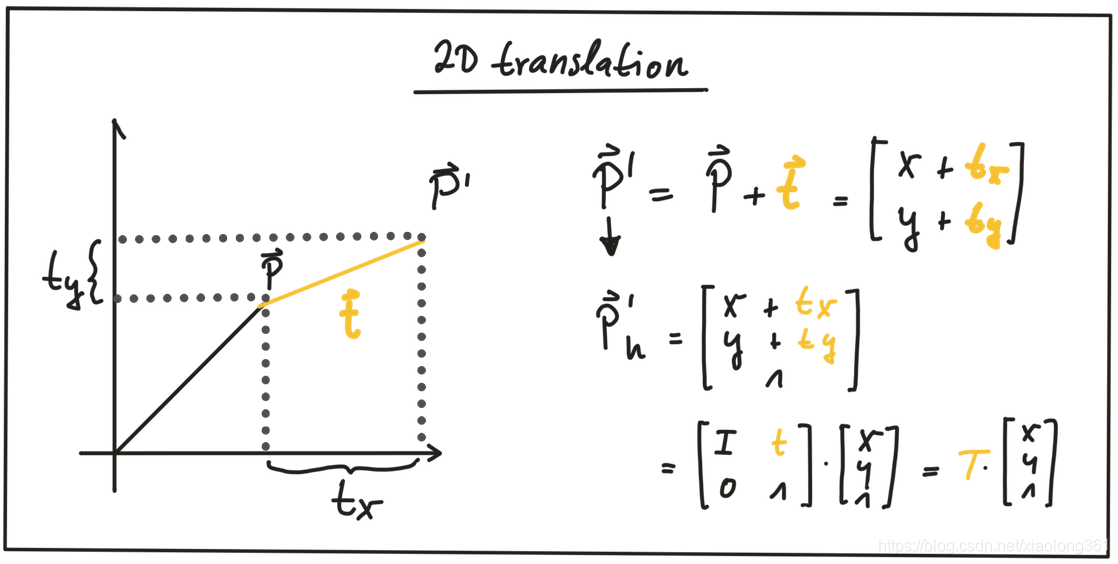
在齐次坐标系中，这可以通过连接一个 $N$维单位矩阵 $I$进行表示，其中 N是 $\overrightarrow{P}$和 $\overrightarrow{t}$的元素个数。这样，平移操作就变成了一个简单的矩阵-向量乘法，如上图所示。

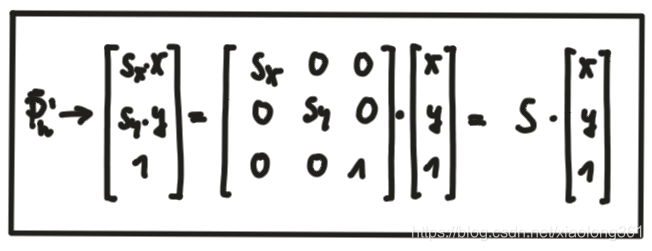
缩放：旋转操作可以通过令 $\overrightarrow{P}$乘以一个缩放向量 $\overrightarrow{s}$实现。在齐次坐标中，这也可以表示为矩阵-向量乘法，如下图所示。

旋转：逆时针方向（在数学上为正）旋转得到的点 $\overrightarrow{P^{'}}$，可以由 $\overrightarrow{P}$通过下图所示的方式得到。

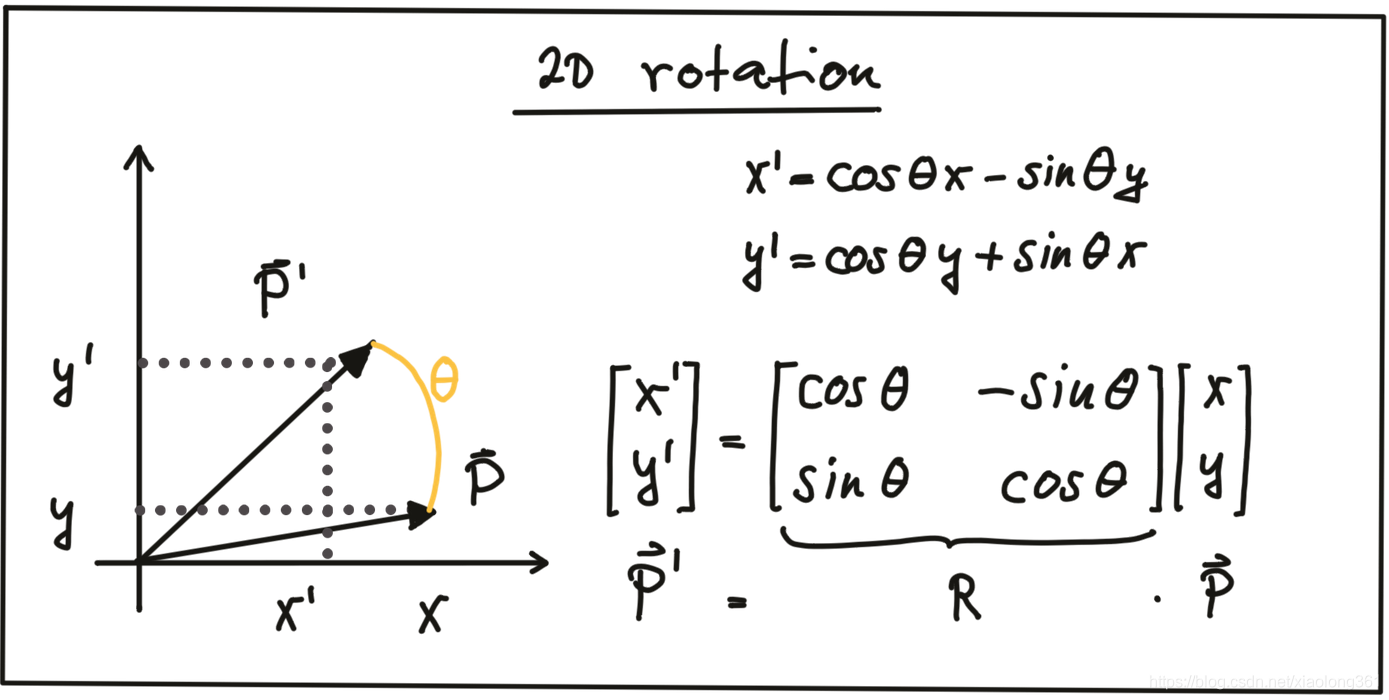
如上图所示，旋转操作可以通过乘以一个旋转矩阵R来表示。在三维空间中，点 $P$可以用下图所示的旋转矩阵表示围绕三个坐标轴的旋转：

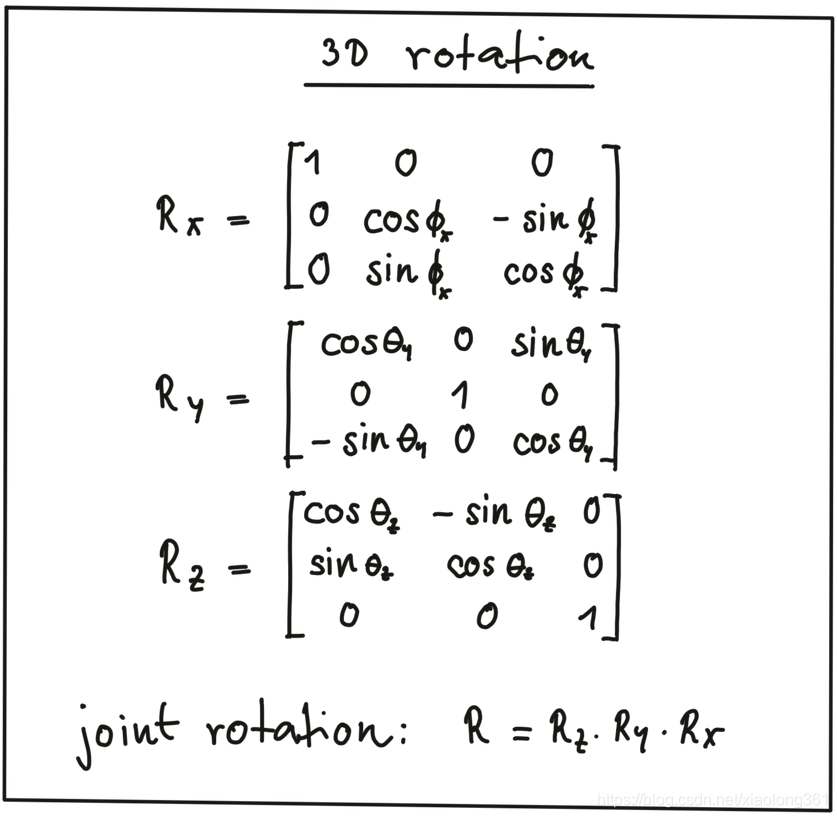
注意：围绕三个坐标轴的独立的旋转可以通过旋转矩阵相乘组合成一个联合旋转矩阵R：
$R=R_z \cdot R_y \cdot R_x$

齐次坐标系的一大优势就是只需连接多个矩阵-向量乘法就可以轻松组合多种转换操作，实乃一大利器！

包含 $R$和 $\overrightarrow{t}$的组合矩阵又被称之为外参矩阵，因为它模拟了点在坐标系之间的坐标转换。一旦激光雷达坐标系中的点被转换到相机坐标系中，下面就需要将其映射到相机图像平面中。为了实现这个目的，我们还要额外添加之前讨论过的相机内参矩阵 $K$。在齐次坐标系下，我们只需将之前的转换结果与内参矩阵相乘就可以实现。

由此可得，完整的将激光雷达3D点云映射到相机图像上所需的坐标转换公式如下图所示：

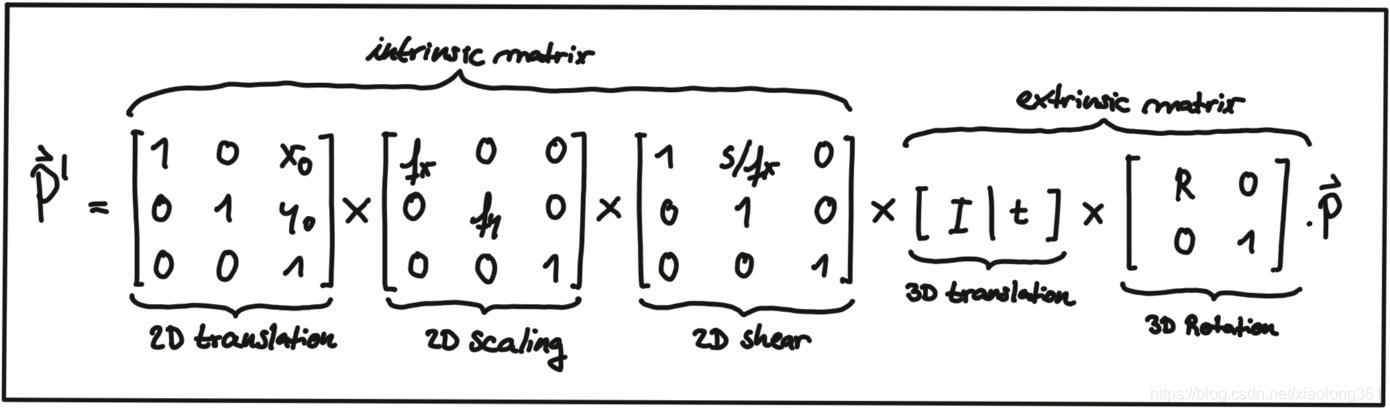
注意：上图中，“缩放”操作已经被集成到了内参矩阵 $K$中（和焦距成为相关量），而不再是外参矩阵的一部分。在下面的视频中，展示了相机的外参对图像平面上物体外观显示的影响：http://ksimek.github.io/perspective_camera_toy.html