2020牛客寒假算法基础集训营1 J题 u's的影响力【矩阵快速幂+欧拉降幂】（全网最详细题解，完整思路）

题目传送门：https://ac.nowcoder.com/acm/contest/3002/J

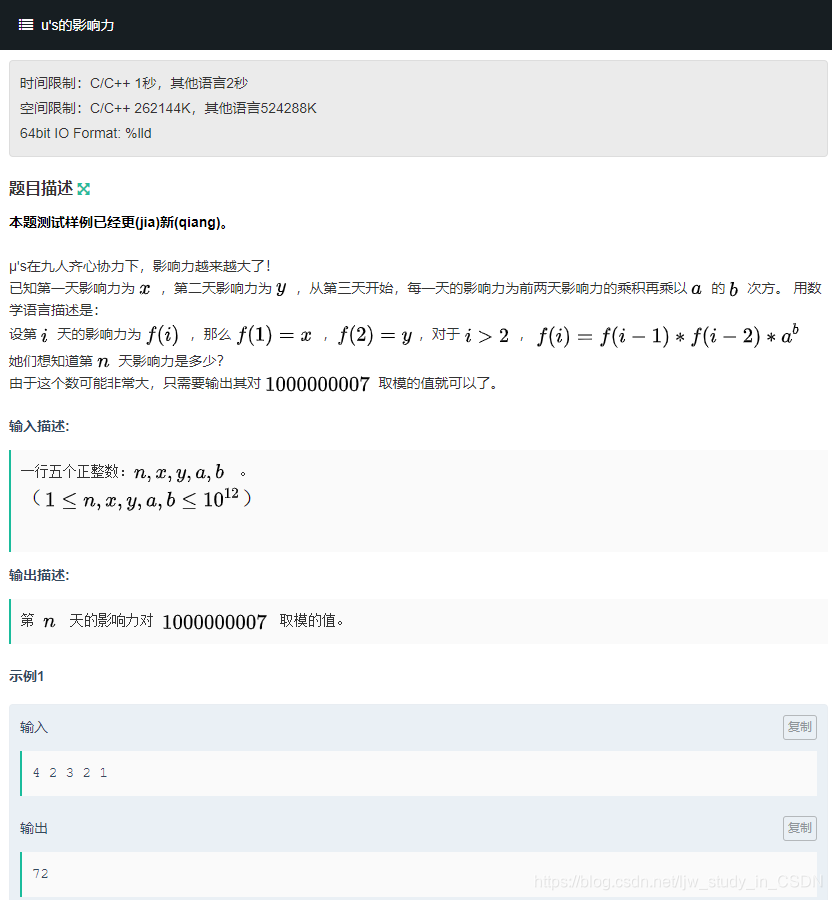
牛客“基础”算法训练营出的题很有意思啊，非常适合我这种萌新学习（真的十分“基础”，我差点就信了）。

今天终于把这题给补了，这相当于是一个模板套模板的题，下面说说我的思路。

完整思路：

首先写出前几项的表达式，找一下规律。

$f(1)=x$

$f(2)=y$

$f(3)=x^1*y^1*(a^b)^1$

$f(4)=x^1*y^2*(a^b)^{2}$

$f(5)=x^2*y^3*(a^b)^{4}$

$f(6)=x^3*y^5*(a^b)^{7}$

$f(7)=x^5*y^8*(a^b)^{12}$

扫描二维码关注公众号，回复： 9395608 查看本文章

写到这里，可以看出很明显的规律了：从第三项开始，x，y的指数是斐波那契数列， 比如说x的指数从第三项开始依次是1,1,2,3,5，y的指数从第三项开始依次是1,2,3,5,8。
把a^b看成一个整体，a^b的指数 = x的指数 + y的指数 - 1。

我们先求x的指数，因为求了x的指数，就能求y的指数，y的指数是x的指数对应的斐波那契数列的后一项，接着a^b的指数也可以算出来。

为了方便表述，设x的指数为k1，y的指数为k2，a^b的指数为k3，当n>=3时，有：

$f(n)=x^{k1}*y^{k2}*(a^b)^{k3}$

对于k1满足的斐波那契数列F(n)，有：

$F(1)=1，F(2)=1$

$F(n)=F(n-1)+F(n-2)（n>=3）$

单独研究F(n)，这就是矩阵快速幂的模板题了，先把递推式 F(n)=F(n-1)+F(n-2) 写成矩阵相乘形式：

$\begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix} * \begin{bmatrix} F(n-1) \\ F(n-2) \\ \end{bmatrix} = \begin{bmatrix} F(n) \\ F(n-1) \\ \end{bmatrix}$

把常数矩阵设为A，写成：

$A* \begin{bmatrix} F(n-1) \\ F(n-2) \\ \end{bmatrix} = \begin{bmatrix} F(n) \\ F(n-1) \\ \end{bmatrix}，其中A=\begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix}$

当n>=2时(若n=2，矩阵A的0次幂为单位矩阵E)，有：
$A^{n-2}* \begin{bmatrix} F(2) \\ F(1) \\ \end{bmatrix} = \begin{bmatrix} F(n) \\ F(n-1) \\ \end{bmatrix}(n>=2)，其中A=\begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix}$

得到了以上的式子，那么矩阵A^n-2可以直接套用矩阵快速幂，F(2),F(1)已知，假设A^n-2=S（矩阵下标从0开始），有：
$\begin{bmatrix}S_{00} & S_{01} \\ S_{10} &S_{11} \\ \end{bmatrix} * \begin{bmatrix} F(2) \\ F(1) \\ \end{bmatrix} = \begin{bmatrix} F(n) \\ F(n-1) \\ \end{bmatrix}(n>=2)，其中S=A^{n-2}$

那么 $F(n)=S_{00}*F(2)+S_{01}*F(1)=S_{00}+S_{01}$。
这样我们就能在 $O(8*logn)$ 的复杂度下求出F(n)。（快速幂是logn，每次2*2的两个矩阵相乘有三层循环为8）

接下来，注意下标的转换。因为F(n)的下标是从1开始的，但是f(n)的下标是从3开始才是斐波那契数列，所以题目输入的n要减去2才是x的指数在斐波那契数列中的下标，所以x的指数k1=F(n-2)，y的指数k2=F(n-1)， 注意前提是必须满足 n-2>=2&&n-1>=2 即 n>=4。当n<4时特判即可。

注意运算结果f(n)要对1e9+7取模，设p=1e9+7，有：

$f(n)=x^{k1}*y^{k2}*(a^b)^{k3} \%p$

这个时候需要用到欧拉降幂了。p为素数，则 φ(p)=p-1。如果底数x与p不互质，那么x%p==0，答案一定是0；如果底数x与p互质，那么可以直接对指数进行降幂，也就是把指数k1对φ(p)取模。

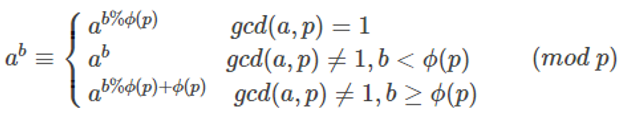
好，做到这里，这道题基本上就做完了。

写代码的时候可以先把底数x,y,a对p取模，特判有0的情况。还有要特判n<4的答案，因为这时候不能用矩阵快速幂。最后就是注意写快速幂取模的时候想清楚是对p取模，还是对φ(p)取模，矩阵快速幂是为了求指数，所以矩阵快速幂要对φ(p)取模，降幂之后的公式用普通快速幂，是对p取模。

AC代码：（4ms）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p=1e9+7,mod=p-1;//矩阵快速幂对mod取模，底数对p取模
ll n,x,y,a,b;
struct node
{
    ll m[2][2];
};
node E={//单位矩阵
1,0,
0,1};
node A={//斐波那契基础矩阵
1,1,
1,0};
node mul(node a,node b)//两矩阵相乘
{
    node s;
    memset(s.m,0,sizeof(s.m));
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            for(int k=0;k<2;k++)
            s.m[i][j]=(s.m[i][j]+a.m[i][k]*b.m[k][j]%mod)%mod;
    return s;
}
node matrix_pow(node a,ll b)//矩阵快速幂，求矩阵a的b次幂
{
    node s=E;
    while(b)
    {
        if(b&1)s=mul(s,a);
        b=b/2;
        a=mul(a,a);
    }
    return s;
}
ll qpow(ll a,ll b)//普通快速幂，求a^b%p
{
    ll s=1;
    while(b)
    {
        if(b&1)s=s*a%p;
        b=b/2;
        a=a*a%p;
    }
    return s;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>x>>y>>a>>b;
    x=x%p;
    y=y%p;
    a=a%p;
    if(x==0||y==0||a==0)printf("0\n");
    else if(n==1)printf("%lld\n",x);
    else if(n==2)printf("%lld\n",y);
    else if(n==3)printf("%lld\n",x*y%p*qpow(a,b)%p);
    else
    {
        ll kx=n-2;//x指数是在斐波那契第几项
        ll ky=n-1;//y指数是在斐波那契第几项
        node s1=matrix_pow(A,kx-2);
        ll k1=(s1.m[0][0]+s1.m[0][1])%mod;//x降幂后的指数
        node s2=matrix_pow(A,ky-2);
        ll k2=(s2.m[0][0]+s2.m[0][1])%mod;//y降幂后的指数
        ll k3=(k1+k2-1+mod)%mod;//a^b降幂后的指数
        ll t=qpow(a,b);
        ll ans=qpow(x,k1)*qpow(y,k2)%p*qpow(t,k3)%p;
        printf("%lld\n",ans);
    }
    return 0;
}

其实这题挺多人都过了，我也不知道为什么要把这“水题”写得这么详细…主要还是自己太菜了。
希望以后见到这种题不要怕，想清楚思路，下次能一发AC（立起了flag…）