【模拟电子技术Analog Electronics Technology 24】—— 信号的运算与处理(1)：基本的运算电路分析

写在前面：在本篇博文中，我将分析几种常见的基本运算电路：比例运算电路，加减运算电路，微分和积分运算电路，指数和对数运算电路输入与输出的关系。但是，掌握单一的运算电路并不是我们的最终目的，因为在题目中，往往是很多个运算电路结合起来的，我们需要学会如何分析

1.比例运算电路

1.1 反向比例运算电路

所谓反向比例运算电路，就是输入信号加在了运放的反相输入端，我们来看看它长什么样：

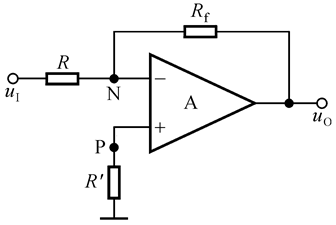
这是反向比例运算电路的构造，当分析电路时遇到这个结构，我们可以直接使用下面的关系： $u_o = -\frac{R_f}{R}u_I$
下面我们来推导一下：
首先，由于虚断，我们得到： $i^+ = i^- = 0$
因此，P点和地等电位，由虚短可知： $u^+ = u_P = u^- = u_N = 0$
对N点列节点电压方程可知： $(\frac{1}{R} + \frac{1}{R_f})u_N - \frac{1}{R_f}u_o = \frac{u_I}{R}$
联立以上式子，可得： $u_o = -\frac{R_f}{R}u_I$

1.下面，我们来讨论一下： $R'$与 $R, R_f$的关系： $R' = R // R_f$，目的是达到静态平衡，即使得两个输入端的外接电阻相等
2. 同时，我们注意到：由于 $u^+ = u^- = 0$，因此该电路无共模输入电压

1.2 同相比例运算电路

对于同相比例运算电路，输入和输出的关系为： $u_o = (1 + \frac{R_f}{R})u_o$
分析方法类似：首先，由于虚断 $i^+ = i^- = 0$，因此， $u_P = u_I$
由虚断可知： $u_N = u_P = u_I$
对反相输入端结点列结点电压方程，得： $(\frac{1}{R} + \frac{1}{R_f})u_N - \frac{1}{R_f}u_o = 0$
整理可得： $u_o = (1 + \frac{R_f}{R})u_o$

注意：由于 $u_N = u_P = u_I$，因此，该电路有共模输入电压： $u_c = u_I$，因此需要特别考虑共模抑制的能力！

2.加减运算电路

2.1求和运算电路

2.1.1 反向求和运算电路

反向求和运算电路输入与输出的关系为： $u_o = -R_f(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})$(可以直接使用）

分析方法呢，也是用结点电压法，这里自己课下可以推导一下就不赘述了

2.1.2 同相求和运算电路

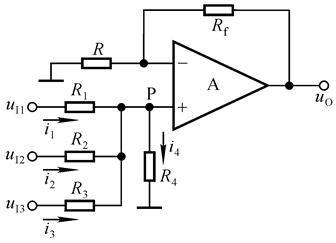
这里就有文章了：
【情况一】：若 $R // R_f = R_1 // R_2 // R_3 // R_4$：
对反相输入端列结点电压方程，得： $(\frac{1}{R} + \frac{1}{R_f})u^- - \frac{1}{R_f}u_o = 0$
对同相输入端列结点电压方程，得： $(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4})u^+ = \frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3}$
由上面第一个式子，我们知道： $u^- = \frac{R}{R + R_f}u_o\tag{1}$
我们令： $R_p = R_1 // R_2 // R_3 // R_4$
那么第二个式子就可以写成： $u^+ = R_p(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})$
联立(1)式，得：
$u_o = R_p(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})\frac{R + R_f}{R}$
这看起来有些复杂，我们有没有化简的办法？—— 有！
我们在等式右边乘一个： $\frac{R_f}{R_f}$，即： $u_o = R_p(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})\frac{R + R_f}{R}\frac{R_f}{R_f}\\ u_o = R_p(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})\frac{R + R_f}{RR_f}R_f\\ u_o = R_p(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})\frac{1}{R_p}R_f\\ u_o = R_f(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})$
那么，在静态平衡的条件下，正向加法运算电路就有： $u_o = R_f(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})$

那么，如果静态不平衡怎么办呢？？
最后就变成了这样： $u_o = R_f\frac{R_P}{R_N}(\frac{u_{I1}}{R_1} + \frac{u_{I2}}{R_2} + \frac{u_{I3}}{R_3})$

2.2 减法运算电路

这个是典型的减法电路，先给出结论：当电路的参数对称时，即上图 $R = R, R_f = R_f$时，
有： $u_o = \frac{R_f}{R}(u_{I1} - u_{I2})$
如果有： $R_1 = R_2 = R_{f1} = R_{f2}$，那么 $u_o = u_{I1} - u_{I2}$
下面，我们也重点推导一下：
先对反相输入端列结点电压方程： $(\frac{1}{R} + \frac{1}{R_f})u^- \frac{1}{R_f}u_o = \frac{u_{I1}}{R}$
然后，我们来看看同相输入电压 $u^+$为多少： $u^+ = \frac{R_f}{R + R_f}u_{I2}$
联立上面的两个式子，得： $u_o = \frac{R_f}{R}(u_{I1} - u_{I2})$

3. 微积分运算电路

3.1 积分运算电路

对于有电容的这种运算放大器，我们最常用的就不再是结点电压法了，而是直接用虚短虚断来处理，我们来看看吧：
首先，对于N点（-），有： $i_R = i_C$(因为虚短)，那么我们就有： $\frac{u_I}{R} = i_C = C\frac{du_C}{dt}$
又因为： $u_C = -u_o$，因此，上式可以化为： $\frac{u_I}{R} = -C\frac{du_o}{dt}$，稍作整理，可得： $u_o = -\frac{1}{RC}\intop u_Idt$，如果是 $t_1$~ $t_2$的时间积分，那么可得： $u_o = -\frac{1}{RC}\int_{t_2}^{t_1}{u_Idt} + u_o(t_1)$

3.2 微分运算电路

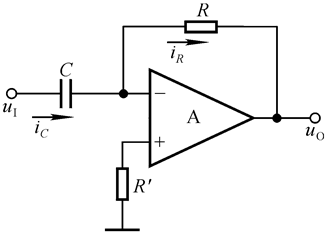
同样地分析方法：N点： $i_C = i_R$，即： $C\frac{du_C}{dt} = -\frac{u_o}{R}$
即： $u_o = -RC\frac{du_C}{dt}$

4.对数和指数运算电路

其实，用二极管或是三极管构成的对数运算电路的分析是和微积分运算电路一样的，只不过，我们需要记住的关键方程就是：

1. 对于二极管： $i_D = I_Se^{\frac{u_D}{U_T}}$
2. 对于三极管： $i_C = I_Se^{\frac{u_{BE}}{U_T}}$

5. 模拟乘法器

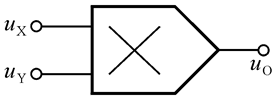
$u_o = ku_Xu_Y$

5.1 模拟乘法器的一些应用

如果把模拟乘法器的两个端口连在一起作为一个输入，那么就变成了乘方运算

如果把模拟乘法器作为反馈支路，那么就变成了除法运算电路：

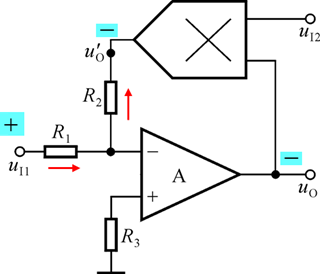
这里我们一起来分析一下这种电路（多个运放的结合是考试的重点！）：
首先，我们第一眼可以看出来的就是反馈支路上的这个模拟乘法器，它的两个输入分别为： $u_0$和 $u_{I2}$，因此，输出 $u_o' = ku_{I2}u_0$,对于A，我们看不出它是什么现成的运算电路，因此，直接用虚断虚短来做：
对于N点：我们有： $\frac{u_{I1}}{R_1} = -\frac{u_0'}{R_2} = -\frac{ku_{I2}u_0}{R_2}$
即： $u_o = -\frac{R_2}{R_1k}\frac{u_{I1}}{u_{I2}}$

当然了，还有许许多多的用法，比如说开方运算等，我们不能一一赘述，但是分析方法确实是一样的