题目:
将整数n分成k份,且每份不能为空,任意两种划分方案不能相同(不考虑顺序)。求整数n分为k份,共有多少种不同的分法。输入两个整数n,k(6<n<=200,2<=k<=6)。输出一个整数,即有几种不同的分法。
思路:
定义一个数组dp[][],dp[i][j]表示将整数 i 划分为 j 份 的方案数。dp[i][j]的动态转移方程为 :
![]()
如何理解该式子呢?首先,如果拿到一个整数 i ,因为题目中要求每份不能为空,因此必须先拿出 j 个数位将 j 份分别放上1,此时剩下 i - j个数。那么剩下的数如何处理呢?可以将其全部分到一份当中(dp[i-j][1]),也可以分到两份中(dp[i-j][2]),...,也可以分到 j 份中(dp[i-j][j]),而每一种分法都是不相同的,所以可以将其全部加起来,和即为dp[i][j]。
不过这个式子看起来并不简洁,为了求得一个简洁的式子,我们再求一个dp[i-1][j-1],
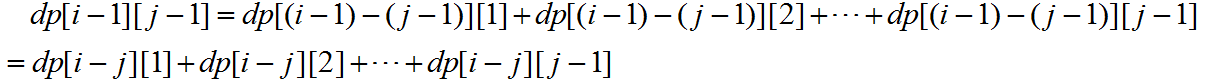
比较上面两个式子可得,
![]()
这就是一个比较简洁的递推式子了,有点类似于高中数学中的裂项相消原理。
这里注意 i , j 的取值范围,i = 1~n,j = 1~ k,但是求dp[i][j]时,必须保证 i>=j(划分的份数不能超过给定的整数)。
另外就是,做了好几道动态规划的题,发现动态转移方程真的好重要(也可以说是递推公式),看似很难很绕的题目,只要提炼出它的动态转移方程,搞清楚遍历的次序以及各变量的取值范围,写程序就相当快了。
代码如下:
// Chapter14_5.cpp : Defines the entry point for the application.
// 数的划分
// 将整数n分成k份,且每份不能为空,任意两种划分方案不能相同(不考虑顺序)。
// 求整数n分为k份,共有多少种不同的分法。
// 输入两个整数n,k(6<n<=200,2<=k<=6)。
// 输出一个整数,即有几种不同的分法。
#include "stdafx.h"
#include<iostream>
using namespace std;
int main()
{
int n,k;
cout << "输入整数n和划分的份数k:";
cin >> n >> k;
int dp[201][7];
//全部初始化为0
memset(dp,0,sizeof(dp));
//对于dp[0][0]作特殊处理(为了后面的动态转移方程能够起作用)
dp[0][0] = 1;
int i,j;
//i的取值范围是1~n(不能超过给定的整数)
for(i=1;i<=n;i++)
//j的范围是1~k(不能超过需要划分的份数)
for(j=1;j<=k;j++)
{
//划分的分数要小于等于该数本身
if(i>=j)
//动态转移方程
dp[i][j] = dp[i-j][j] + dp[i-1][j-1];
}
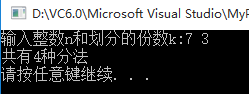
cout << "共有" << dp[n][k] << "种分法" << endl;
system("pause");
return 0;
}运行结果如下: