3.sklearn—聚类分析详解（聚类分析的分类；常用算法；各种距离：欧氏距离、马氏距离、闵式距离、曼哈顿距离、卡方距离、二值变量距离、余弦相似度、皮尔森相关系数、最远（近）距离、重心距离）

版权声明：不要转载复制当原创就好了，指明下参考地址或者书目，大家一起学习进步。 https://blog.csdn.net/Monk_donot_know/article/details/86649339

这一章总结的很痛苦，打公式费时费力。

1.聚类分析

1.1聚类方法

类别	包括的主要算法
划分（分裂）方法	K-Means算法（均值）、K-medoids算法（中心点）、K-modes算法（众数）、k-prototypes算法、CLARANS（基于选择）
层次分析	BIRCH算法（平衡迭代规约）、CURE算法（点聚类）、CHAMELEON（动态模型）
基于密度	DBSCAN（基于高密度连接区域）、DENCLUE（密度分布函数）、OPTICS（对象排序识别）
基于网格	STING（统计信息网络）、CLIOUE（聚类高维空间）、WAVE-CLUSTER（小波变换）
基于模型	统计学方法、神经网络

此外还有，最优分割法（有序样本聚类）、模糊聚类法（应用模糊集理论）、图论聚类…
这个水太深了，看了半天是不是发现自己就只会k均值和birch系统聚类啊…真真真的学无止境

1.2 常见聚类算法：

算法名称	描述
K-Means	K均值算法是一种快速聚类算法，在最小化误差函数的基础上将数据划分为预定的K簇。数据量大的时候也会比较方便和快速。
K-中心点	K均值对孤立点比较敏感，因此这算一个改进算法，不是选择簇中对象的平均值作为簇中心，而是选择簇中离平均值最近的对象作为簇中心。计算量原大于K均值，因此适合小样本数据。
K-众数	顾名思义，不是采用均值作为中心，而是众数。用来处理分类型数据，统计频率即可，弥补K均值只能做数值计算的不足。也是最K均值的改进算法之一。
K-Protype	K均值和K众数的结合，分别用于数值型数据和分类型数据。也是最K均值的改进算法之一。
CLARA	clustering large application，大型应用聚类，基于抽样的方法，采用数据集的多个随机样本，然后使用PAM方法计算各个样本中的最佳中心点。也是最K均值的改进算法之一。
CLARANS	clustering large application basedupon randomized search，基于随机搜索的聚类大型应用。在数据中随机选取K个对象当中心，随机选择一个当前中心点和一个不是当前中心点进行替换，看是否能改善绝对误差，随机搜索L次，组成局部最优解集合。然后重复该过程M次，返回最佳局部最优解。也是最K均值的改进算法之一。
系统聚类	常用的就是那个birch。由高到低成树形结构。适用于小样本数据。

参考博客https://blog.csdn.net/wojiaosusu/article/details/56960103

1.3 cluster提供的聚类算法及其使用范围

函数名称	参数	范围	距离度量
K-means	簇数	大样本、聚类数目中等	点之间的距离公式
spectral clastering	簇数	样本数中等、聚类数目小	图距离
ward hierarchical clustering	簇数	大样本、聚类数目大	点之间的距离
agglomerative clustering	簇数、链接类型、距离	大样本、聚类数目大	任意成对点线图之间的距离
DBSCAN	半径大小、最低成员数	样本数中等、聚类数目中等	最近点之间的距离
birch	分支因子、阈值、可选全局集群	大样本、聚类数目大	点之间的欧式距离

2. 各种距离

参考书目：王宏志,大数据分析原理与实践[M],北京:机器工业出版社,2017.

2.1 连续性变量的距离

2.1.1 欧氏距离

两个n维向量 : $\vec{a}\ (x_{11}, \ x_{12}, ···,\ x_{1n})$ 与 $\vec{b}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$ 之间的欧式距离为：
$d_{12}=\sqrt{\sum_{k=1}^n{(x_{1k}-x_{2k})^2}}$
缺点是不考虑分量之间的相关性。

2.1.2 曼哈顿距离

两个n维向量 $\vec{a}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$与 $\vec{b}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$ 之间的曼哈顿距离为：
$d_{12}=\sum_{k=1}^n{|x_{1k}-x_{2k}|}$

2.1.3 切比雪夫距离

两个n维向量 $\vec{a}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$与 $\vec{b}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$ 之间的切比雪夫距离为：
$d_{12}=\max_{k} \ {|x_{1k}-x_{2k}|}$
等价于：
$d_{12}=\lim_{k\rightarrow+\infty}(\sum_{k=1}^n{|x_{1k}-x_{2k}|^k})^{1/k}$

2.1.4 闵可夫斯基距离

两个n维向量 $\vec{a}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$与 $\vec{b}\ (x_{11},\ x_{12},\ ···,\ x_{1n})$之间的闵可夫斯基夫距离为：
$d_{12}=\sqrt[p] {\sum_{k=1}^n{|x_{1k}-x_{2k}|^p}}$
p是可变参数。根据参数的不同，闵式距离可以表示一类的距离。当p=1时是曼哈顿距离；p=2时是欧氏距离； $p\rightarrow\infty$时，就是切比雪夫距离。
闵式距离的两个缺点：
1.将各个分量的量纲当做相同对待；
2.没有充分考虑各个分量的分布（期望方差可能不同）。

2.1.5 标准欧式距离

$d_{12}=\sqrt{\sum_{k=1}^n{(\frac{x_{1k}-x_{2k}}{s_{k}})^2}}$
$s_{k}$是分量的标准差。

2.1.6 马氏距离

若 $\mu^i$、 $\sum^i$为总体（类别）为第i组 $G^i$的均值向量和协方差矩阵，则X的马氏距离为：
$D^2(x,G^i)=(x-\mu^i)^T(\sum^i)^{-1}(x-\mu^i) \qquad (i=1,2,···,)$
比如在正态分布中，概率密度相同的点分布在同一个椭圆上，虽然欧式距离不同，但是马氏距离相同。所以称马氏距离有相同的“距离”。
马氏距离主要用于两个场景：

• 用来度量两个服从同一分布并且其协方差矩阵为C的随机变量X与Y的差异程度。
• 度量X与某一类的均值向量的差异程度，判别样本的归属。此时Y为类均值样本。

马氏距离的优点在于量纲无关，排除变量之间的相关性干扰。缺点则是不同的特征不能差别对待，可能夸大弱特征。

2.1.7 补充：距离判别法，同样用到马氏距离

给定k组分类，第i组中n条样本记录 $\vec{x_i}\ (x_{i1},\ x_{i2},\ ···,\ x_{ip})$，其中i=1,2,···,每条样本记录有p个属性，样本中心为各个属性的均值 $\vec{\bar{x}}\ (\bar{x_1},\ \bar{x_2},\ ···,\bar{x_p})$，计算洗的点到各个分组的样本中心的距离，并把它归到距离最小的那一组。

2.2 离散型变量距离

2.2.1 卡方距离

每两个个体间各个属性的差异性：值较大说明个体与变量取值有显著关系，个体间变量取值差异较大，也就是说，个体 $\vec{X}(x_{i},···,x_{k})$与个体 $\vec{Y}(y_{i},···,y_{k})$的距离可以加以计算如下：
$CHISQ(x)=\sqrt{\sum_{i=1}^k{\frac{(x_{i}-E(x_{i}))^2}{E(x_{i})}+\frac{(y_{i}-E(y_{i}))^2}{E(y_{i})}}}$

2.2.2 Phi距离

$Phi(x)=\frac{CHISQ(x)}{\sqrt{k}}=\frac{\sqrt{\sum_{i=1}^k{\frac{(x_{i}-E(x_{i}))^2}{E(x_{i})}+\frac{(y_{i}-E(y_{i}))^2}{E(y_{i})}}}} {\sqrt{k}}$

2.2.3 二值变量距离

就是对于K个属性变量均为0、1的情况下，简单匹配系数二值变量距离建立在两两个体间构成的01频数表上，如：

.	个体Y0	个体Y1
个体X0	a个	b个
个体X1	c个	d个

那么：
$S(x,y)=\frac{b+c}{a+b+c+d}$
b+c是差异性，a+d是相似性。

2.2.4 Jaccard系数

$J=\frac{d}{b+c+d}$
相比于二值变量距离，这个分母排除了同时为0的情况。

2.3基于相似系数的相似性度量（用相似度表示距离）

2.3.1 余弦相似度

两个向量夹角的余弦值。注重的是两个向量在方向上的差异。常用语比较文档之间的相似性。
以二维空间为例， $\vec{A}\ (x_{1},\ y_{1})$与$ \vec{B}\ (x_{2},\ y_{2})$之间的余弦相似度为：
$\cos\theta = \frac{x_1 x_2+y_1 y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}$
取值范围是[-1,1]。 $\theta$取值在[0, $\pi$]。

2.3.2 汉明距离

1111与1001之间的汉明距离为2。
信息论中，两个登场字符串之间的汉明距离是指，一个变化为另一个对应位置的不同字符数。

2.3.3 Jaccard相似系数

先空着

2.3.4 皮尔森相关系数

统计量皮尔森相关系数r:

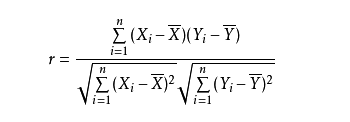
分别对X和Y基于自身总体标准化后计算空间向量的余弦夹角：
$r(X,Y)=\frac{n\sum{xy} -\sum{x}\sum{y}} {\sqrt{n\sum{x^2}-(\sum{x})^2} \cdot \sqrt{n\sum{y^2}-(\sum{y})^2} }$

2.4 个体与类以及类间的亲疏关系度量

2.4.1 最远（近）距离

各个小类中的个体距离的最大（小）值。

2.4.2 组间平均链锁距离

两小类之间的距离是所有样本对间的平均距离。

2.4.3 组内平均链锁距离

除了考虑组间样本对的距离，还有组内所有样本对的距离，所有距离求均值。

2.4.4 重心距离

求类重心，也就是求所有样本在各个变量上的均值，用类重心之间的距离衡量类之间的距离。

2.4.5 离差平方和距离（Ward方法）

聚类过程中，每个小类之间计算合并后的离差平方和，并将值最小的凝聚成一类。

3. 常用的聚类目标函数

对于一个新的聚类方法，去看文献的时候，最难的部分就是理解作者构造的目标函数。

3.1 连续属性的SSE

$SSE=\sum_{i=1}^K{\sum_{x\in{E_{i}}}{dist(e_{i},x)^2}}$

3.2 文档数据的SSE计算公式：

$SSE=\sum_{i=1}^K{\sum_{x\in{E_{i}}}{\cos(e_{i},x)^2}}$

3.3 簇 $E_i$的聚类中心 $e_i$计算公式：

$e_i=\frac1n \sum_{x\in{E_{i}}}{x}$