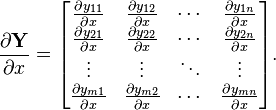通过一个例子快速上手矩阵求导 转载自：https://blog.csdn.net/nomadlx53/article/details/50849941

转载自：https://blog.csdn.net/nomadlx53/article/details/50849941

前提及说明

第一次遇见矩阵求导，大多数人都是一头雾水，而搜了维基百科看也还是云里雾里，一堆的名词和一堆的表格到底都是什么呢？这里总结了我个人的学习经验，并且通过一个例子可以让你感受如何进行矩阵求导，下次再遇到需要进行矩阵求导的地方就不会措手不及。

在进行概念的解说之前，首先大家需要先知道下面的这个前提：

前提： 若 xx 为向量，则默认 xx 为列向量， xTxT 为行向量

布局的概念

布局简单地理解就是分子 yy 、分母 xx 是行向量还是列向量。

• 分子布局（Numerator-layout）： 分子为 yy 或者分母为 xTxT (即，分子为列向量或者分母为行向量)
• 分母布局（Denominator-layout）： 分子为 yTyT 或者分母为 xx (即，分子为行向量或者分母为列向量)

为了更加深刻地理解两种布局的特点和区别，下面是从维基百科中布局部分拿来的例子：

分子布局

• 标量/向量：  （分母的向量为行向量）

• 向量/标量：  （分子的向量为列向量）

• 向量/向量：  （分子为列向量横向平铺，分母为行向量纵向平铺）

• 标量/矩阵：  （注意这个矩阵部分是转置的，而下面的分母布局是非转置的）

• 矩阵/标量： 

分母布局

• 标量/向量：  （分母的向量为列向量）

• 向量/标量：  （分子的向量为行向量）

• 向量/向量：  （分子为行向量纵向平铺，分母为列向量横向平铺）

• 标量/矩阵：  （矩阵部分为原始矩阵）

一个求导的例子

问题

∂(y−Xw)T(y−Xw)∂w∂(y−Xw)T(y−Xw)∂w

说明： y、wy、w为列向量，XX为矩阵

式子演化

看到这个例子不要急着去查表求导，先看看它的形式，是u(w)∗v(w)u(w)∗v(w)的形式，这种形式一般求导较为复杂，因此为了简化运算，我们先把式子展开成下面的样子（注意：(Xw)T=wTXT(Xw)T=wTXT）： 

∂(yTy−yTXw−wTXTy+wTXTXw)∂w∂(yTy−yTXw−wTXTy+wTXTXw)∂w

然后就可以写成四个部分求导的形式如下（累加后求导=求导后累加）： 

∂yTy∂w−∂yTXw∂w−∂wTXTy∂w+∂wTXTXw∂w∂yTy∂w−∂yTXw∂w−∂wTXTy∂w+∂wTXTXw∂w

求导

• ∂yTy∂w∂yTy∂w求导 : ∂yTy∂w=0∂yTy∂w=0

说明：分子部分为标量，分母部分为向量，找到维基百科中的Scalar-by-vector identities表格，在表格中匹配形式到第1行的位置，因为分母为列向量，因此为分母布局，对应的求导结果就是 00 。

---

• ∂yTXw∂w∂yTXw∂w求导 : ∂yTXw∂w=XTy∂yTXw∂w=XTy

说明：同样的，在维基百科中的Scalar-by-vector identities表格，在表格中匹配形式到第11行的位置，对应的求导结果就是 XTyXTy 。

---

• ∂wTXTy∂w∂wTXTy∂w求导 : ∂wTXTy∂w=∂(wTXTy)T∂w=∂yTXw∂w=XTy∂wTXTy∂w=∂(wTXTy)T∂w=∂yTXw∂w=XTy

说明：因为分子为标量，标量的转置等于本身，所以对分子进行转置操作，其等价于第二部分。

---

• ∂wTXTXw∂w∂wTXTXw∂w求导 : ∂wTXTXw∂w=2XTXw∂wTXTXw∂w=2XTXw

说明：同样的，在维基百科中的Scalar-by-vector identities表格，在表格中匹配形式到第13行的位置，矩阵的转置乘上本身（XTXXTX）为对称矩阵当做表格中的AA ，所以得到求导结果 2XTXw2XTXw 。

整合

把四个部分求导结果进行相应的加减就可以得到最终的结果： 

∂yTy∂w−∂yTXw∂w−∂wTXTy∂w+∂wTXTXw∂w=0−XTy−XTy+2XTXw=−2XT(y+Xw)∂yTy∂w−∂yTXw∂w−∂wTXTy∂w+∂wTXTXw∂w=0−XTy−XTy+2XTXw=−2XT(y+Xw)

现在你再看看维基百科里那成堆的表格，是不是觉得异常实用了！

参考文献

• 维基百科 Matrix calculus
• 求导的例子来自《机器学习实战》-第八章 回归 138页