什么是范数?
范数(Norm)是数学中的一种概念,用于度量向量、矩阵等大小或距离的概念。
范数可以简单的理解为“距离”。因为向量既有大小又有方向,因此向量是不能直接比较大小。范数提供了一种方法,可以将所有的向量转化为一个实数,来比较向量的大小。
范数可以等于点到坐标零点的距离。
通俗的说,范数就是为了方便度量而人为定义的一种度量方法,主要就是面对复杂空间和多维数组时,选取出一个统一的量化标准,以方便度量和比较。
向量范数
向量范数表征向量空间中向量的大小。
向量的L-1范数
向量的L1范数是向量中各个元素绝对值之和,计算公式如下:
![]()
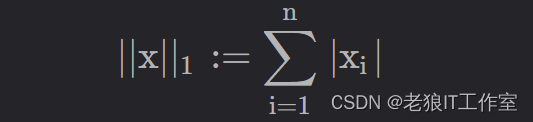
向量的L-2范数
向量的L2范数(二阶范数)是向量中各个元素平方和再开方的结果,计算公式如下:

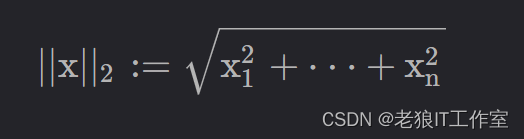
向量的L-P范数
向量的LP范数是指对向量中各个元素进行P次方求和,然后对和开P次方根。
计算公式如下:

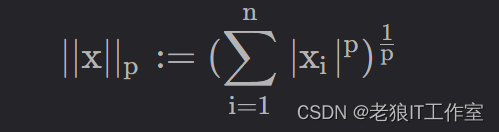
当P取2时,就是L-2范数;当P取1时,就是L-1范数。
向量的L∞范数
正无穷范数:所有元素中绝对值最大的。
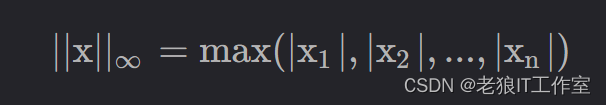
负无穷范数:所有元素中绝对值最小的。
什么是向量间的距离?
我们经常需要计算向量间的差异,进而评价向量的相似性和类别等信息。空间中两个向量之间的距离就是两个向量相似性的一种反映。根据数据特性的不同,可以采用不同的度量方法。一般而言,定义一个函数 d(x, y) , 若它是一种“距离度量”,则需要满足下面的基本性质:
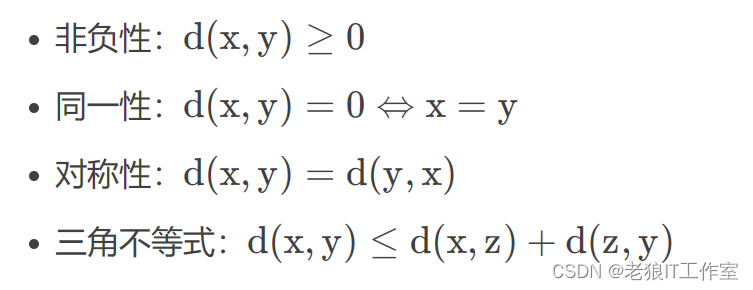
向量间距离的L-P范数计算公式如下:
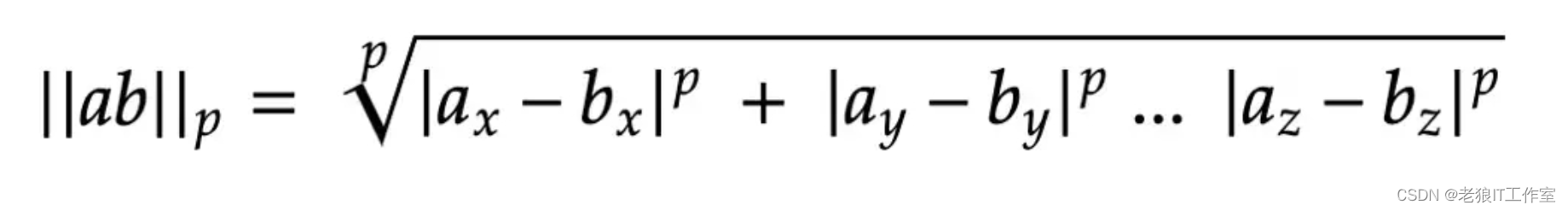
假设二维平面上有A(2,3)和B(3,1)两个点,如图所示:

A,B同时也是两个向量,套用L-2范数计算公式,可以计算出向量A(2,3)的L-2范数范数约为:3.6,这个值也是向量A的模,即A点到原点(0,0)的距离。
同理,向量B(3,1)的L-2范数范数约为:3.16,即向量B(3,1)到0原点(0,0)的距离是3.16。
向量A到向量B的距离怎么算呢?套用上面的公式,可得结果约为2.236, 计算过程如下:
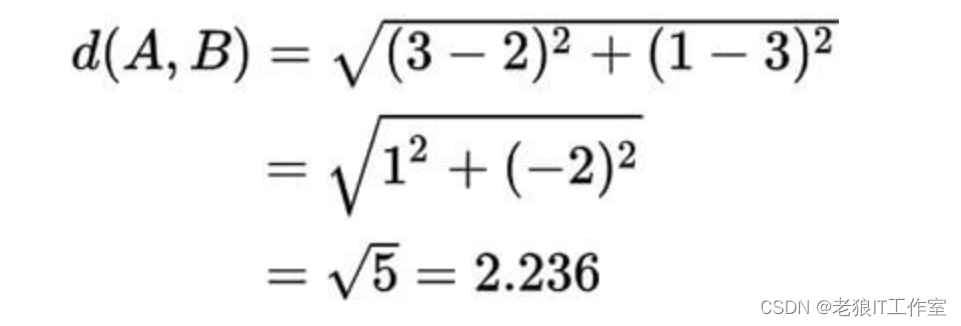
常见的向量间距离:
假设X和Y都是一个n维的向量,如下图所示:
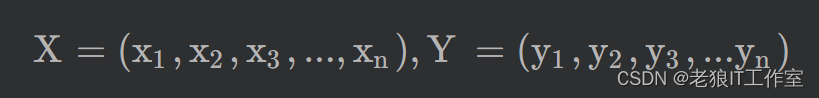
曼哈顿距离和欧式距离(欧几里得距离)
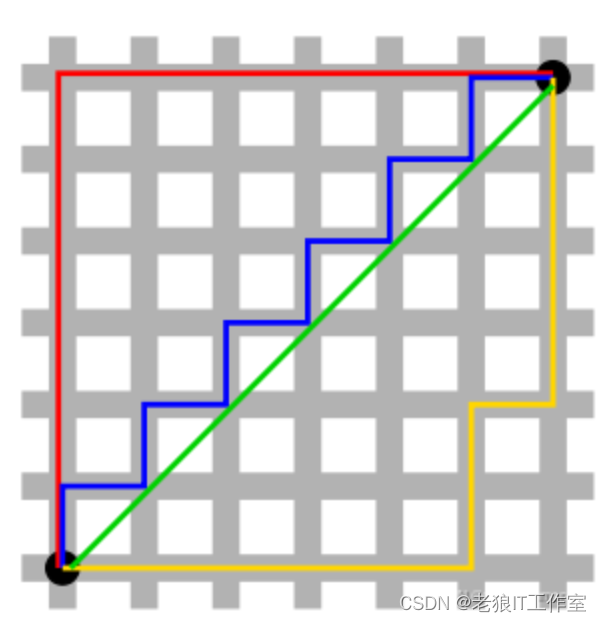
曼哈顿距离(Manhattan Distance)又称为城市街区距离,是指在一个网格状的城市街区中,从一个点到另一个点沿着直角路径所经过的格子数。
n维空间的曼哈顿距离的计算公式如下:
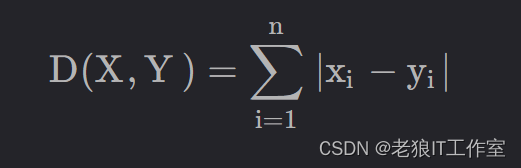
向量的L-1范数可以看做是曼哈顿距离的特例,y向量为0。
n维空间的欧式距离的计算公式如下:
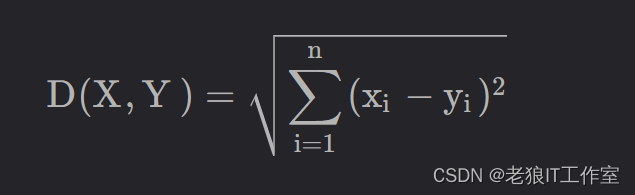
向量的L-2范数可以看做是欧式距离的特例,y向量为0。
上图中红线代表曼哈顿距离,而蓝色和黄色代表等价的曼哈顿距离。绿色代表欧氏距离,也就是直线距离。
切比雪夫距离
切比雪夫距离是将2个点之间的距离定义为其各坐标数值差的最大值,计算公式如下:
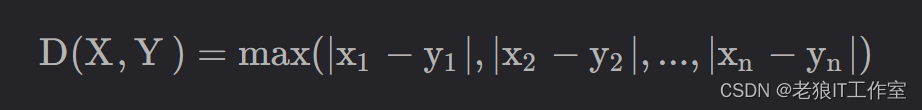
向量的L无穷范数可以看做是切比雪夫距离的特例,y向量为0。
闵可夫斯基距离

向量的L-P范数可以看做是闵可夫斯基距离的特例,y向量为0。
Numpy中如何计算向量或矩阵范数
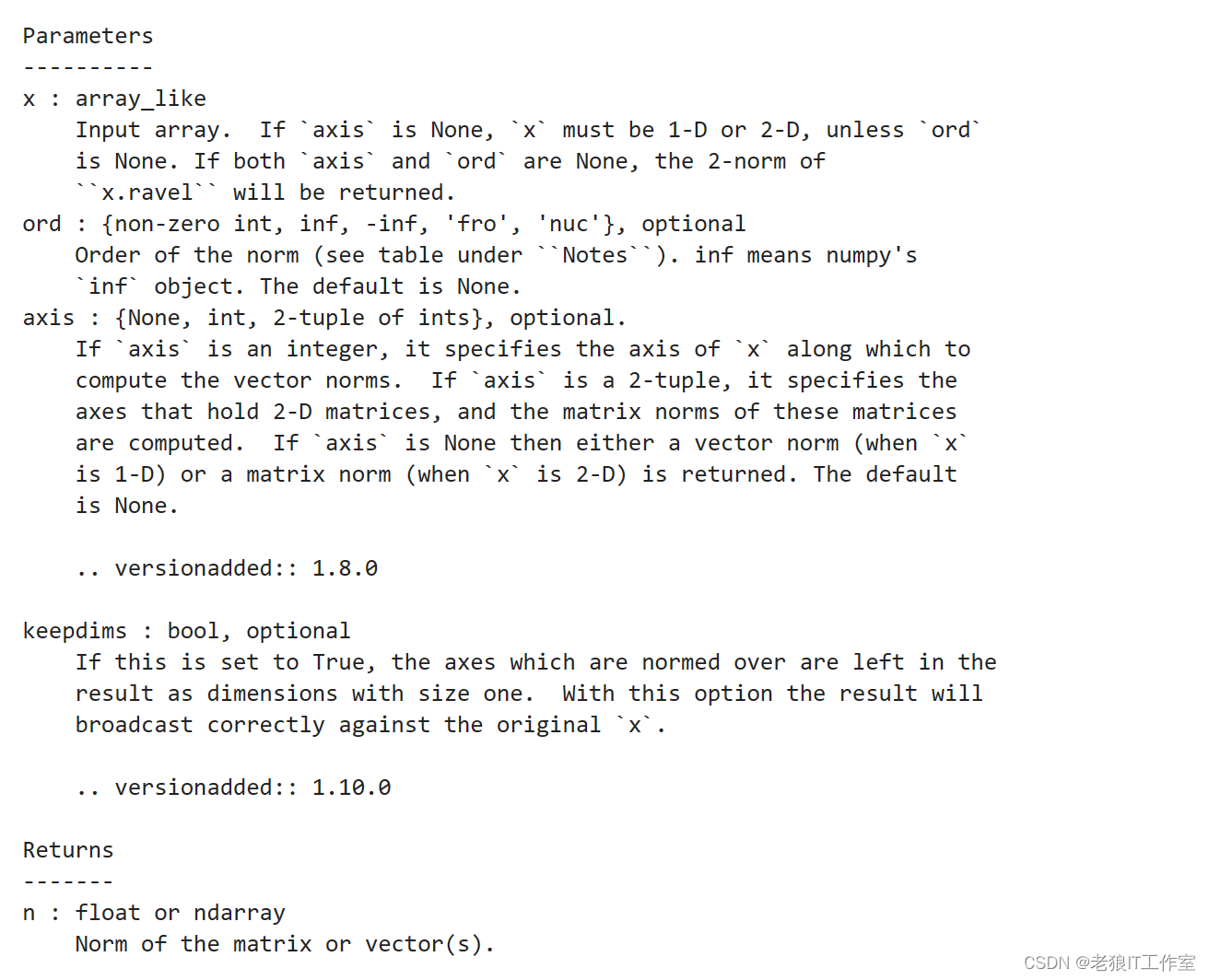
numpy.linalg.norm函数是numpy库中的一个函数,用于计算向量或矩阵的范数。其函数原型如下:
numpy.linalg.norm(x, ord=None, axis=None, keepdims=False)
其中,参数说明如下:
x:输入的数组或向量。ord:范数的类型,可以取以下值之一:
- None:默认为2范数,即欧几里得范数。
- 1:L1范数,即将向量中各个元素绝对值之和作为范数。
- np.inf:无穷范数,即将向量中各个元素绝对值的最大值作为范数。
- -np.inf:负无穷范数,即将向量中各个元素绝对值的最小值作为范数。
axis:指定沿哪个轴计算范数,如果不指定则默认对整个数组进行计算。keepdims:是否保持输出结果的维度与输入结果一致,默认为False。
计算向量和矩阵L1范数
import numpy as np
# 创建一个3x3的矩阵
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 计算L1范数
l1_norm = np.linalg.norm(a, ord=1)
print("矩阵的L1范数为:", l1_norm)
l1_norm_c = np.linalg.norm(a, ord=1, axis=0)
print("列向量L1范数为:", l1_norm_c)
l1_norm_r = np.linalg.norm(a, ord=1, axis=1)
print("行向量L1范数为:", l1_norm_r)

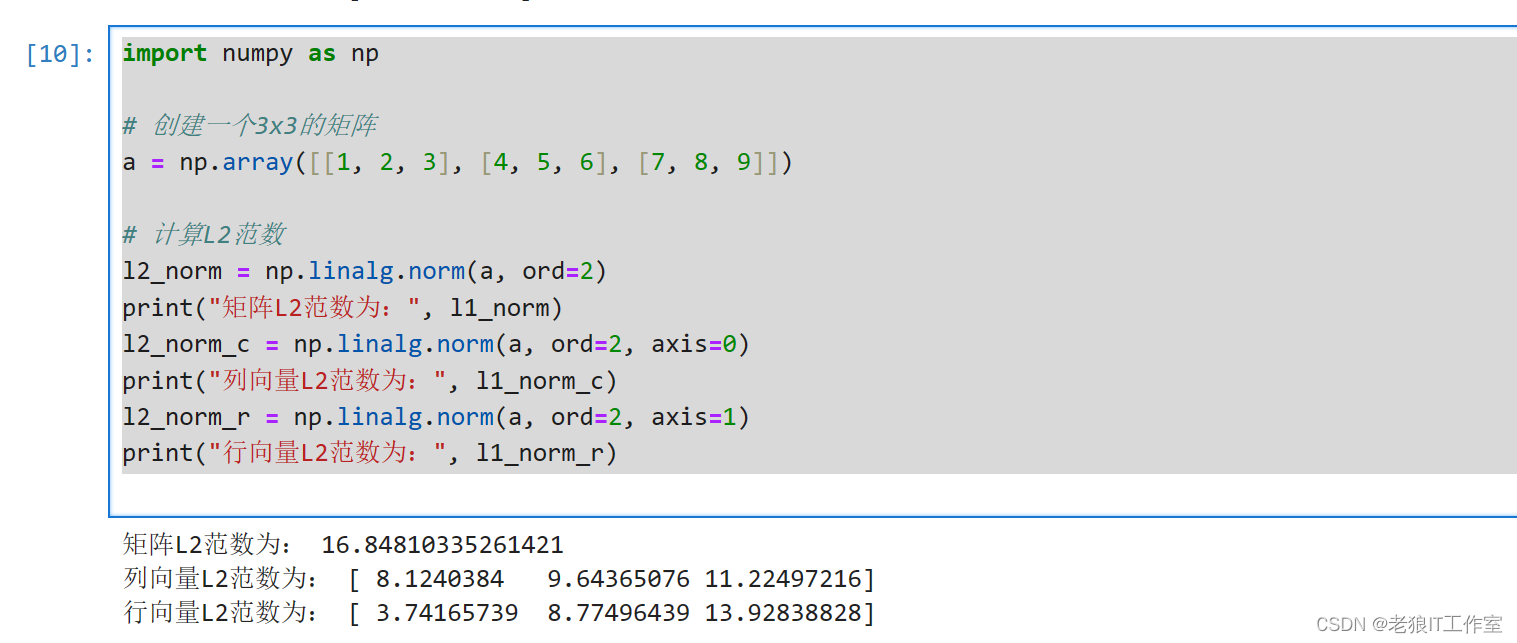
计算向量和矩阵L2范数
import numpy as np
# 创建一个3x3的矩阵
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 计算L2范数
l2_norm = np.linalg.norm(a, ord=2)
print("矩阵L2范数为:", l1_norm)
l2_norm_c = np.linalg.norm(a, ord=2, axis=0)
print("列向量L2范数为:", l1_norm_c)
l2_norm_r = np.linalg.norm(a, ord=2, axis=1)
print("行向量L2范数为:", l1_norm_r)
计算向量的无穷范数
import numpy as np
# 创建一个一维的矩阵
a = np.array([-11, 2, 3, 4, 5, 6, 7, 8, 9])
# 计算负无穷范数
n_inf_norm = np.linalg.norm(a, ord=-np.inf)
print("矩阵负无穷范数为:", n_inf_norm)
# 计算正无穷范数
p_inf_norm = np.linalg.norm(a, ord=np.inf)
print("矩阵正无穷范数为:", p_inf_norm)
计算向量间的曼哈顿距离
import numpy as np
def manhattan_distance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.sum(np.abs(x-y))
x = [1, 3, 5]
y = [2, 4, 6]
print('x-y:',manhattan_distance(x, y))
print('y-x:',manhattan_distance(y, x)) 计算向量间的欧式(欧几里得距离)
计算向量间的欧式(欧几里得距离)
import numpy as np
def euclidean_distance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.sqrt(np.sum(np.square(x-y)))
x = [1, 3, 5]
y = [2, 4, 6]
print('x-y:',euclidean_distance(x, y))
print('y-x:',euclidean_distance(y, x))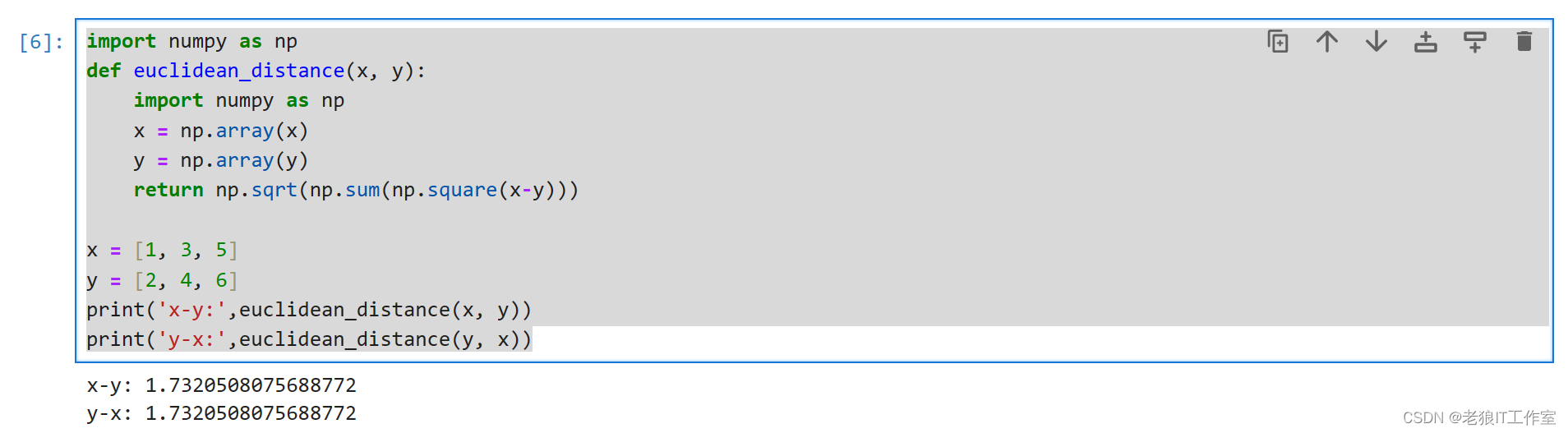
计算向量间的闵可夫斯基距离
import numpy as np
def minkowski_distance(x, y, p):
import math
import numpy as np
xy= zip(x, y)
return math.pow(np.sum([math.pow(np.abs(i[0]-i[1]), p) for i in xy]), 1/p)
x = [1, 3, 5]
y = [2, 4, 6]
print('x-y:',minkowski_distance(x, y, 3))
print('y-x:',minkowski_distance(y, x, 3)) 
计算向量间的切比雪夫距离
import numpy as np
# 切比雪夫距离
def chebyshev_distance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.max(np.abs(x-y))
x = [10, 3, 5]
y = [2, 4, 16]
print('x-y:',chebyshev_distance(x, y))
print('y-x:',chebyshev_distance(y, x))
参考资料
机器学习中的数学——距离定义(二):曼哈顿距离(Manhattan Distance)
机器学习中的数学——距离定义(一):欧几里得距离(Euclidean Distance)