文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。
文章全部链接:
基础知识点
Part1:三角函数系的正交性
Part2:T=2π的周期函数的傅里叶级数展开
Part3:周期为T=2L的函数展开
Part4:傅里叶级数的复数形式
Part5:从傅里叶级数推导傅里叶变换
总结
文章目录
基础知识点
设 α \alpha α为任意角
f ( 2 k π + α ) = f α ( k ∈ Z ) ,其中 f 为 s i n 或 c o s 或 t a n 或 c o t s i n ( π + α ) = − s i n α c o s ( π + α ) = − c o s α t a n ( π + α ) = t a n α c o t ( π + α ) = c o t α s i n ( − α ) = − s i n α c o s ( − α ) = c o s α t a n ( π + α ) = − t a n α c o t ( π + α ) = − c o t α s i n ( π − α ) = s i n α c o s ( π − α ) = − c o s α t a n ( π − α ) = − t a n α c o t ( π − α ) = − c o t α s i n ( 2 π − α ) = − s i n α c o s ( 2 π − α ) = c o s α t a n ( 2 π − α ) = − t a n α c o t ( 2 π − α ) = − c o t α \begin{align} & f(2k \pi + \alpha) = f \alpha (k \in Z) ,其中f为 sin或cos或tan或cot \\ \\ & sin(\pi + \alpha) = -sin \alpha \\ & cos(\pi + \alpha) = -cos \alpha \\ & tan(\pi + \alpha) = tan \alpha \\ & cot(\pi + \alpha) = cot \alpha \\ \\ & sin(- \alpha) = - sin \alpha \\ & cos(- \alpha) = cos \alpha \\ & tan(\pi + \alpha) = -tan \alpha \\ & cot(\pi + \alpha) = -cot \alpha \\ \\ & sin(\pi - \alpha) = sin \alpha \\ & cos(\pi - \alpha) = - cos \alpha \\ & tan(\pi - \alpha) = - tan \alpha \\ & cot(\pi - \alpha) = -cot \alpha \\ \\ & sin(2 \pi - \alpha) = -sin \alpha \\ & cos(2 \pi - \alpha) = cos \alpha \\ & tan(2 \pi - \alpha) = -tan \alpha \\ & cot(2 \pi - \alpha) = -cot \alpha & \end{align} f(2kπ+α)=fα(k∈Z),其中f为sin或cos或tan或cotsin(π+α)=−sinαcos(π+α)=−cosαtan(π+α)=tanαcot(π+α)=cotαsin(−α)=−sinαcos(−α)=cosαtan(π+α)=−tanαcot(π+α)=−cotαsin(π−α)=sinαcos(π−α)=−cosαtan(π−α)=−tanαcot(π−α)=−cotαsin(2π−α)=−sinαcos(2π−α)=cosαtan(2π−α)=−tanαcot(2π−α)=−cotα
积化和差公式:
sin α cos β = sin ( α + β ) + sin ( α − β ) 2 cos α sin β = sin ( α + β ) − sin ( α − β ) 2 cos α cos β = cos ( α + β ) + cos ( α − β ) 2 sin α sin β = − cos ( α + β ) − cos ( α − β ) 2 \begin{align} & \sin \alpha \cos \beta ={\sin(\alpha +\beta )+\sin(\alpha -\beta ) \over 2} \\ & \cos \alpha \sin \beta ={\sin(\alpha +\beta )-\sin(\alpha -\beta ) \over 2} \\ & \cos \alpha \cos \beta ={\cos(\alpha +\beta )+\cos(\alpha -\beta ) \over 2}\\ & \sin \alpha \sin \beta =-{\cos(\alpha +\beta )-\cos(\alpha -\beta ) \over 2} & \end{align} sinαcosβ=2sin(α+β)+sin(α−β)cosαsinβ=2sin(α+β)−sin(α−β)cosαcosβ=2cos(α+β)+cos(α−β)sinαsinβ=−2cos(α+β)−cos(α−β)
和差化积公式:
s i n α + s i n β = 2 s i n α + β 2 c o s α − β 2 s i n α − s i n β = 2 c o s α + β 2 s i n α − β 2 c o s α + c o s β = 2 c o s α + β 2 c o s α − β 2 c o s α − c o s β = − 2 s i n α + β 2 s i n α − β 2 \begin{align} & sin \alpha + sin \beta = 2sin\frac {\alpha + \beta} {2} cos \frac {\alpha - \beta} {2} \\ & sin \alpha - sin \beta = 2cos\frac {\alpha + \beta} {2} sin \frac {\alpha - \beta} {2} \\ & cos \alpha + cos \beta = 2 cos\frac {\alpha + \beta} {2} cos \frac {\alpha - \beta} {2} \\ & cos \alpha - cos \beta = - 2 sin\frac {\alpha + \beta} {2} sin \frac {\alpha - \beta} {2} & \end{align} sinα+sinβ=2sin2α+βcos2α−βsinα−sinβ=2cos2α+βsin2α−βcosα+cosβ=2cos2α+βcos2α−βcosα−cosβ=−2sin2α+βsin2α−β
倍角公式:
s i n 2 α = s i n α c o s α + s i n α c o s α = 2 s i n α c o s α c o s 2 α = c o s 2 α − s i n 2 α = 2 c o s 2 α − 1 = 1 − 2 s i n 2 α c o s 2 α = 1 + c o s 2 α 2 s i n 2 α = 1 − c o s 2 α 2 t a n 2 α = 2 t a n α 1 − t a n 2 α \begin{align} & sin 2 \alpha = sin \alpha cos \alpha + sin \alpha cos \alpha = 2 sin \alpha cos \alpha \\ & cos 2 \alpha = cos^2 \alpha - sin ^2 \alpha =2 cos ^ 2 \alpha -1 = 1- 2 sin^2 \alpha \\ & cos ^ 2 \alpha = \frac{1 + cos 2 \alpha}{2} \\ & sin^ 2 \alpha = \frac{1 - cos 2 \alpha}{2} \\ & tan 2 \alpha = \frac {2 tan \alpha} {1 - tan ^2 \alpha} & \end{align} sin2α=sinαcosα+sinαcosα=2sinαcosαcos2α=cos2α−sin2α=2cos2α−1=1−2sin2αcos2α=21+cos2αsin2α=21−cos2αtan2α=1−tan2α2tanα
三角函数导数:
正弦函数: ( s i n x ) ′ = c o s x 余弦函数: ( c o s x ) ′ = − s i n x 正切函数: ( t a n x ) ′ = s e c 2 x 余切函数: ( c o t x ) ′ = − c s c 2 x \begin{align} & 正弦函数: (sin x)' = cosx \\ & 余弦函数: (cos x)' = -sinx \\ & 正切函数: (tan x )' = sec^2 x \\ & 余切函数: (cot x)' = -csc^2x & \end{align} 正弦函数:(sinx)′=cosx余弦函数:(cosx)′=−sinx正切函数:(tanx)′=sec2x余切函数:(cotx)′=−csc2x
积分性质:
性质 1 :如果 c 是常数, ∫ a b c d x = c ( b − a ) ; 性质 2 :如果 c 是常数, ∫ z b c f ( x ) d x = c ∫ a b f ( x ) d x ; 性质 3 : ∫ a b [ f ( x ) ± g ( x ) ] d x = ∫ a b f ( x ) d x ± ∫ z b g ( x ) d x ; \begin{align} & 性质1:如果c是常数,\int_{a}^{b} cdx = c(b-a); \\ & 性质2:如果c是常数,\int_z^b cf(x)dx = c \int_a^b f(x)dx; \\ & 性质3:\int_{a}^{b}[f(x) \pm g(x)] dx = \int_a^b f(x)dx \pm \int_z^b g(x)dx; & \end{align} 性质1:如果c是常数,∫abcdx=c(b−a);性质2:如果c是常数,∫zbcf(x)dx=c∫abf(x)dx;性质3:∫ab[f(x)±g(x)]dx=∫abf(x)dx±∫zbg(x)dx;
Part1:三角函数系的正交性
三角函数系集合: { 0 , 1 , s i n x , c o s x , s i n 2 x , c o s 2 x , . . . , s i n n x , c o s n x , . . . } \{0,1,sin x, cos x, sin 2x, cos 2x, ...,sin nx, cos nx, ...\} { 0,1,sinx,cosx,sin2x,cos2x,...,sinnx,cosnx,...},即为 { s i n n x , c o s n x } \{sin nx, cos nx\} { sinnx,cosnx},其中 n = 0 , 1 , 2 , . . . n = 0, 1,2,... n=0,1,2,...。
对于两个向量 a ⃗ \vec{a} a和 b ⃗ \vec {b} b,如果它们的内积等于0,表示这两个向量是垂直的,具有正交性。即 a ⃗ ⋅ b ⃗ = 0 \vec{a} \cdot \vec{b} = 0 a⋅b=0,如下示意图, a ⃗ ⋅ b ⃗ = 2 ∗ − 1 + 1 ∗ 2 = 0 \vec{a} \cdot \vec{b} = 2*-1 + 1*2 = 0 a⋅b=2∗−1+1∗2=0。
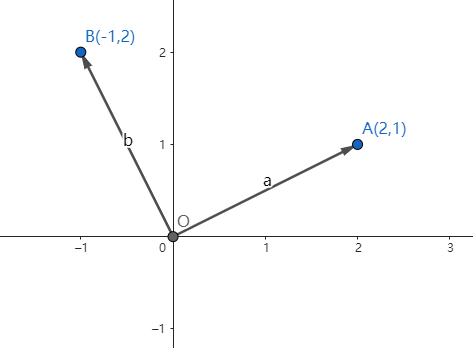
若向量 a ⃗ \vec{a} a和向量 b ⃗ \vec{b} b中包含三个元素,分别是 ( a 1 , a 2 , a 3 ) (a_1, a_2, a_3) (a1,a2,a3)和 ( b 1 , b 2 , b 3 ) (b_1, b_2, b_3) (b1,b2,b3),如果 a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 + a 3 b 3 = 0 \vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 = 0 a⋅b=a1b1+a2b2+a3b3=0,那么 a ⃗ \vec{a} a与 b ⃗ \vec {b} b正交。
再推广到 a ⃗ \vec a a和 b ⃗ \vec b b中有 n n n个元素,分别为 { a 1 , a 2 , a 3 , . . . , a n } \{ a_1, a_2, a_3, ..., a_n \} { a1,a2,a3,...,an}和 { b 1 , b 2 , b 3 , . . . , b n } \{ b_1, b_2, b_3, ... , b_n \} { b1,b2,b3,...,bn},如果 a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 + a 3 b 3 + . . a n b n = ∑ i = 1 n a i b i = 0 \vec a \cdot \vec b = a_1 b_1 + a_2 b_2 + a_3 b_3 + .. a_n b_n = \sum_{i=1} ^ {n} a_i b_i = 0 a⋅b=a1b1+a2b2+a3b3+..anbn=∑i=1naibi=0,那么 a ⃗ \vec a a与 b ⃗ \vec b b正交。
再扩展,如果 a = f ( x ) a = f(x) a=f(x), b = g ( x ) b = g(x) b=g(x),在一个区间内如 [ x 0 , x 1 ] [x_0, x_1] [x0,x1]计算 a ⋅ b a \cdot b a⋅b即 f ( x ) ⋅ g ( x ) f(x) \cdot g(x) f(x)⋅g(x),也就是计算在区间 [ x 0 , x 1 ] [x_0, x_1] [x0,x1]内的面积和,相当于求积分 ∫ x 0 x 1 f ( x ) g ( x ) d x \int_{x_0}^{x_1} f(x) g(x)dx ∫x0x1f(x)g(x)dx。如果 ∫ x 0 x 1 f ( x ) g ( x ) d x = 0 \int_{x_0}^{x_1} f(x) g(x)dx=0 ∫x0x1f(x)g(x)dx=0,就可以说 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)这两个函数正交。
再说回到三角函数的正交性的定义:从三角函数系集合中任取两项,在 [ − π , π ] [-\pi, \pi] [−π,π]之间,这两项的积分等于0。
即:
∫ − π π s i n ( n x ) c o s ( m x ) d x = 0 ∫ − π π c o s ( n x ) s i n ( m x ) d x = 0 ∫ − π π s i n ( n x ) s i n ( m x ) d x = 0 ∫ − π π c o s ( n x ) c o s ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) cos (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) sin (mx) dx = 0 \\ & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx = 0 & \end{align} ∫−ππsin(nx)cos(mx)dx=0∫−ππcos(nx)sin(mx)dx=0∫−ππsin(nx)sin(mx)dx=0∫−ππcos(nx)cos(mx)dx=0
接下来证明三角函数的正交性。
当 m ≠ n m \ne n m=n时,由积化和差公式 s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sin \alpha cos \beta = \frac{1}{2} [sin(\alpha + \beta) + sin(\alpha - \beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) c o s ( m x ) d x = 1 2 [ ∫ − π π s i n ( n + m ) x d x + ∫ − π π s i n ( n − m ) x d x ] = 1 2 [ ( − 1 n + m c o s ( n + m ) x ∣ − π π ) + ( − 1 n − m c o s ( n − m ) x ∣ − π π ) ] = 1 2 [ − c o s ( n + m ) π − c o s ( − ( n + m ) π ) n + m + [ − c o s ( n − m ) π − c o s ( − ( n − m ) π ) n − m ] ] 有 c o s ( − α ) = c o s α ,很容易得出上式为 0 , 即: ∫ − π π s i n ( n x ) c o s ( m x ) d x = 0 \begin{align} &\int_{- \pi}^{\pi} sin (nx) cos (mx) dx \\ & = \frac {1}{2} \left [ \int_{- \pi}^{\pi} sin(n + m)x dx + \int_{- \pi}^{\pi}sin(n-m)x dx \right] \\ & = \frac{1}{2} \left[ (- \frac{1}{n+m} cos(n+m)x |_{- \pi}^{\pi}) + (- \frac{1}{n-m} cos(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [- \frac{cos(n+m) \pi - cos(-(n+m)\pi)}{n+m} + [- \frac{cos(n-m) \pi - cos(-(n-m)\pi) }{n-m} ] \right ] \\ & 有cos (-\alpha) = cos \alpha,很容易得出上式为0 , 即: \int_{- \pi}^{\pi} sin (nx) cos (mx) dx = 0 & \end{align} ∫−ππsin(nx)cos(mx)dx=21[∫−ππsin(n+m)xdx+∫−ππsin(n−m)xdx]=21[(−n+m1cos(n+m)x∣−ππ)+(−n−m1cos(n−m)x∣−ππ)]=21[−n+mcos(n+m)π−cos(−(n+m)π)+[−n−mcos(n−m)π−cos(−(n−m)π)]]有cos(−α)=cosα,很容易得出上式为0,即:∫−ππsin(nx)cos(mx)dx=0
当 m ≠ n m \ne n m=n时,由积化和差公式 c o s α s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] cos\alpha sin\beta = \frac{1}{2} [sin(\alpha + \beta) - sin(\alpha - \beta)] cosαsinβ=21[sin(α+β)−sin(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π c o s ( n x ) s i n ( m x ) d x = 1 2 [ ∫ − π π s i n ( n + m ) x d x − ∫ − π π s i n ( n − m ) x d x ] = 1 2 [ ( − 1 n + m ) c o s ( n + m ) x ∣ − π π ) − ( − 1 n − m ) c o s ( n − m ) x ∣ − π π ) ] = 1 2 [ [ − [ c o s ( n + m ) π − c o s ( − ( n + m ) π ) ] n + m ] − [ − [ c o s ( n − m ) π − c o s ( − ( n − m ) π ) ] n − m ] ] 有 c o s ( − α ) = c o s α ,很容易得出上式为 0 , 即: ∫ − π π c o s ( n x ) s i n ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} cos (nx) sin (mx) dx \\ & =\frac {1}{2} \left [ \int_{- \pi}^{\pi} sin(n + m)x dx - \int_{- \pi}^{\pi}sin(n-m)x dx \right] \\ & = \frac{1}{2} \left[ (- \frac{1}{n+m}) cos(n+m)x |_{- \pi}^{\pi}) - (- \frac{1}{n-m} )cos(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [ [- \frac{\left[ cos(n+m) \pi - cos(-(n+m)\pi) \right]}{n+m}] - [- \frac{\left[ cos(n-m) \pi - cos(-(n-m)\pi) \right]}{n-m} ] \right ] \\ & 有cos (-\alpha) = cos \alpha,很容易得出上式为0 , 即: \int_{- \pi}^{\pi} cos (nx) sin (mx) dx = 0 & \end{align} ∫−ππcos(nx)sin(mx)dx=21[∫−ππsin(n+m)xdx−∫−ππsin(n−m)xdx]=21[(−n+m1)cos(n+m)x∣−ππ)−(−n−m1)cos(n−m)x∣−ππ)]=21[[−n+m[cos(n+m)π−cos(−(n+m)π)]]−[−n−m[cos(n−m)π−cos(−(n−m)π)]]]有cos(−α)=cosα,很容易得出上式为0,即:∫−ππcos(nx)sin(mx)dx=0
当 m ≠ n m \ne n m=n时,由积化和差公式 c o s α c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] cos\alpha cos\beta = \frac{1}{2} [cos(\alpha + \beta) + cos(\alpha - \beta)] cosαcosβ=21[cos(α+β)+cos(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π c o s ( n x ) c o s ( m x ) d x = 1 2 [ ∫ − π π c o s ( n + m ) x d x + ∫ − π π c o s ( n − m ) x d x ] = 1 2 [ 1 n + m s i n ( n + m ) x ∣ − π π ) + 1 n − m s i n ( n − m ) x ∣ − π π ) ] = 1 2 [ [ s i n ( n + m ) π − s i n ( − ( n + m ) π ) ] n + m + [ s i n ( n − m ) π − s i n ( − ( n − m ) π ) ] n − m ] 有 s i n ( − α ) = − s i n α , 又有 ∣ s i n k π + α ∣ = ∣ s i n α ∣ , 上式中 α = 0 , s i n ( ( n + m ) ) π = s i n ( ( n − m ) π ) = 0 很容易得出上式为 0 , 即: ∫ − π π c o s ( n x ) c o s ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx \\ & =\frac {1}{2} \left [ \int_{- \pi}^{\pi} cos(n + m)x dx + \int_{- \pi}^{\pi}cos(n-m)x dx \right] \\ & = \frac{1}{2} \left[ \frac{1}{n+m} sin(n+m)x |_{- \pi}^{\pi}) + \frac{1}{n-m} sin(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [ \frac{\left[ sin(n+m) \pi - sin(-(n+m)\pi) \right]}{n+m} + \frac{\left[ sin(n-m) \pi - sin(-(n-m)\pi) \right]}{n-m} \right ] \\ & 有 sin (-\alpha) = - sin \alpha,又有|sin k \pi + \alpha| = |sin \alpha|,\\ & 上式中\alpha=0, sin ( (n+m)) \pi = sin((n-m) \pi) = 0很容易得出上式为0 , 即: \\ & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx = 0 & \end{align} ∫−ππcos(nx)cos(mx)dx=21[∫−ππcos(n+m)xdx+∫−ππcos(n−m)xdx]=21[n+m1sin(n+m)x∣−ππ)+n−m1sin(n−m)x∣−ππ)]=21[n+m[sin(n+m)π−sin(−(n+m)π)]+n−m[sin(n−m)π−sin(−(n−m)π)]]有sin(−α)=−sinα,又有∣sinkπ+α∣=∣sinα∣,上式中α=0,sin((n+m))π=sin((n−m)π)=0很容易得出上式为0,即:∫−ππcos(nx)cos(mx)dx=0
当 m ≠ n m \ne n m=n时,由积化和差公式 s i n α s i n β = 1 2 [ c o s ( α + β ) − c o s ( α − β ) ] sin\alpha sin\beta = \frac{1}{2} [cos(\alpha + \beta) - cos(\alpha - \beta)] sinαsinβ=21[cos(α+β)−cos(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) s i n ( m x ) d x = 1 2 [ ∫ − π π c o s ( n + m ) x d x − ∫ − π π c o s ( n − m ) x d x ] = 1 2 [ 1 n + m s i n ( n + m ) x ∣ − π π ) − 1 n − m s i n ( n − m ) x ∣ − π π ) ] = 1 2 [ [ s i n ( n + m ) π − s i n ( − ( n + m ) π ) ] n + m − [ s i n ( n − m ) π − s i n ( − ( n − m ) π ) ] n − m ] 有 ∣ s i n ( k π + α ) ∣ = ∣ s i n α ∣ , 上式中 α = 0 , s i n ( ( n + m ) ) π = s i n ( ( n − m ) π ) = 0 很容易得出上式为 0 , 即: ∫ − π π s i n ( n x ) s i n ( m x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx \\ &=\frac {1}{2} \left [ \int_{- \pi}^{\pi} cos(n + m)x dx - \int_{- \pi}^{\pi}cos(n-m)x dx \right] \\ & = \frac{1}{2} \left[ \frac{1}{n+m} sin(n+m)x |_{- \pi}^{\pi}) - \frac{1}{n-m} sin(n-m)x |_{- \pi}^{\pi}) \right] \\ & = \frac{1}{2} \left [ \frac{\left[ sin(n+m) \pi - sin(-(n+m)\pi) \right]}{n+m} - \frac{\left[ sin(n-m) \pi - sin(-(n-m)\pi) \right] }{n-m} \right ] \\ & 有 | sin (k \pi + \alpha)| = | sin \alpha |, 上式中\alpha=0, sin ( (n+m)) \pi = sin( (n-m) \pi) = 0\\ &很容易得出上式为0 , 即: \\ & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx = 0 & \end{align} ∫−ππsin(nx)sin(mx)dx=21[∫−ππcos(n+m)xdx−∫−ππcos(n−m)xdx]=21[n+m1sin(n+m)x∣−ππ)−n−m1sin(n−m)x∣−ππ)]=21[n+m[sin(n+m)π−sin(−(n+m)π)]−n−m[sin(n−m)π−sin(−(n−m)π)]]有∣sin(kπ+α)∣=∣sinα∣,上式中α=0,sin((n+m))π=sin((n−m)π)=0很容易得出上式为0,即:∫−ππsin(nx)sin(mx)dx=0
当 m = n m=n m=n时, 由三角函数平方公式 s i n 2 α = 1 2 ( 1 − c o s 2 α ) sin ^ 2 \alpha = \frac{1}{2} (1 - cos 2 \alpha) sin2α=21(1−cos2α)、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) s i n ( n x ) d x = 1 2 [ ∫ − π π ( 1 − c o s 2 n x ) d x ] = 1 2 [ ∫ − π π 1 d x − ∫ − π π c o s 2 n x d x ] 如果 m = n = 0 ,上式 = 0 ; 如果 m = n ≠ 0 , 可以假定 c o s 2 n x = c o s 0 x c o s 2 n x , 根据三角函数的正交性质,那么右边 ∫ − π π c o s 2 n x d x = 0 ,上式即为 1 2 [ x ∣ − π π ] = 1 2 2 π = π \begin{align} &\int_{-\pi}^{\pi} sin (nx) sin (nx) dx = \frac{1}{2} \left [ \int_{-\pi}^{\pi} (1 - cos2nx) dx \right ] = \frac{1}{2} \left [ \int_{-\pi}^{\pi} 1 dx - \int_{-\pi}^{\pi} cos2nx dx \right ] \\ & 如果m=n=0,上式=0;\\ & 如果m=n \ne 0, 可以假定cos2nx = cos 0x cos 2nx,\\ & 根据三角函数的正交性质,那么右边\int_{-\pi}^{\pi} cos2nx dx = 0 ,上式即为 \\ & \frac{1}{2} \left[ x|_{-\pi}^{\pi}\right] = \frac{1}{2} 2\pi = \pi & \end{align} ∫−ππsin(nx)sin(nx)dx=21[∫−ππ(1−cos2nx)dx]=21[∫−ππ1dx−∫−ππcos2nxdx]如果m=n=0,上式=0;如果m=n=0,可以假定cos2nx=cos0xcos2nx,根据三角函数的正交性质,那么右边∫−ππcos2nxdx=0,上式即为21[x∣−ππ]=212π=π
当 m = n m=n m=n时, 由三角函数平方公式 c o s 2 α = 1 2 ( 1 + c o s 2 α ) cos^ 2 \alpha = \frac{1}{2} (1 + cos 2 \alpha) cos2α=21(1+cos2α)、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π c o s ( n x ) c o s ( n x ) d x = 1 2 [ ∫ − π π ( 1 + c o s 2 n x ) d x ] = 1 2 [ ∫ − π π 1 d x + ∫ − π π c o s 2 n x d x ] 如果 m = n = 0 ,上式变为 1 2 [ ∫ − π π 2 d x ] = x ∣ − π π = 2 π ; 如果 m = n ≠ 0 , 假定 c o s 2 n x = c o s 0 x c o s 2 n x ,根据三角函数的正交性质, 那么右边 ∫ − π π c o s 2 n x d x = 0 ,上式即为 1 2 [ x ∣ − π π ] = 1 2 2 π = π \begin{align} & \int_{-\pi}^{\pi} cos (nx) cos (nx) dx = \frac{1}{2} \left [ \int_{-\pi}^{\pi} (1 + cos2nx) dx \right ] = \frac{1}{2} \left [ \int_{-\pi}^{\pi} 1 dx + \int_{-\pi}^{\pi} cos2nx dx \right ] \\ & 如果m=n=0,上式变为\frac{1}{2} \left [ \int_{-\pi}^{\pi} 2 dx \right ] = x|_{-\pi}^{\pi} = 2\pi;\\ & 如果m=n \ne 0, 假定cos2nx = cos 0x cos 2nx,根据三角函数的正交性质,\\ & 那么右边\int_{-\pi}^{\pi} cos2nx dx = 0 ,上式即为 \\ & \frac{1}{2} \left[ x|_{-\pi}^{\pi}\right] = \frac{1}{2} 2\pi = \pi & \end{align} ∫−ππcos(nx)cos(nx)dx=21[∫−ππ(1+cos2nx)dx]=21[∫−ππ1dx+∫−ππcos2nxdx]如果m=n=0,上式变为21[∫−ππ2dx]=x∣−ππ=2π;如果m=n=0,假定cos2nx=cos0xcos2nx,根据三角函数的正交性质,那么右边∫−ππcos2nxdx=0,上式即为21[x∣−ππ]=212π=π
当 m = n m=n m=n时, 由积化和差公式 s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sin \alpha cos \beta = \frac{1}{2} [sin(\alpha + \beta) + sin(\alpha - \beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]、复合导数求导、三角函数常用导数公式以及积分性质可证:
∫ − π π s i n ( n x ) c o s ( n x ) d x = ∫ − π π c o s ( n x ) s i n ( n x ) d x = 1 2 [ ∫ − π π s i n 2 n x d x + ∫ − π π s i n 0 x d x ] 当 m = n = 0 时,左边变为 ∫ − π π 0 d x = 0 ,右边计算也为 0 ,所以 ∫ − π π s i n ( n x ) c o s ( n x ) d x = 0 当 m = n ≠ 0 时,左边可以看作 ∫ − π π c o s 0 x s i n 2 n x d x = 0 ,所以 ∫ − π π s i n ( n x ) c o s ( n x ) d x = 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) cos (nx) dx = \int_{- \pi}^{\pi} cos (nx) sin (nx) dx =\frac {1}{2} \left [ \int_{- \pi}^{\pi} sin2nx dx + \int_{- \pi}^{\pi}sin0x dx \right] \\ & 当m=n=0时,左边变为\int_{- \pi}^{\pi} 0 dx = 0,右边计算也为0,所以 \int_{- \pi}^{\pi} sin (nx) cos (nx) dx = 0 \\ & 当m=n \ne 0时, 左边可以看作\int_{- \pi}^{\pi} cos0x sin 2nxdx = 0,所以 \int_{- \pi}^{\pi} sin (nx) cos (nx) dx = 0 & \end{align} ∫−ππsin(nx)cos(nx)dx=∫−ππcos(nx)sin(nx)dx=21[∫−ππsin2nxdx+∫−ππsin0xdx]当m=n=0时,左边变为∫−ππ0dx=0,右边计算也为0,所以∫−ππsin(nx)cos(nx)dx=0当m=n=0时,左边可以看作∫−ππcos0xsin2nxdx=0,所以∫−ππsin(nx)cos(nx)dx=0
总结如下:
∫ − π π s i n ( n x ) c o s ( m x ) d x = 0 ∫ − π π c o s ( n x ) s i n ( m x ) d x = 0 ∫ − π π c o s ( n x ) c o s ( m x ) d x = { 0 , m ≠ n 2 π , m = n = 0 π m = n ≠ 0 ∫ − π π s i n ( n x ) s i n ( m x ) d x = { 0 , m ≠ n 或 m = n = 0 π m = n ≠ 0 \begin{align} & \int_{- \pi}^{\pi} sin (nx) cos (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) sin (mx) dx = 0 \\ & \int_{- \pi}^{\pi} cos (nx) cos (mx) dx = \left\{\begin{matrix} 0, & m \ne n \\ 2 \pi, & m = n =0 \\ \pi & m = n \ne 0 \end{matrix}\right.\\ & \int_{- \pi}^{\pi} sin (nx) sin (mx) dx = \left\{\begin{matrix} 0, & m \ne n 或 m=n=0\\ \pi & m = n \ne 0 \end{matrix}\right. & \end{align} ∫−ππsin(nx)cos(mx)dx=0∫−ππcos(nx)sin(mx)dx=0∫−ππcos(nx)cos(mx)dx=⎩ ⎨ ⎧0,2π,πm=nm=n=0m=n=0∫−ππsin(nx)sin(mx)dx={ 0,πm=n或m=n=0m=n=0