0.摘要
由Witkin引入的尺度空间技术涉及使用高斯核将原始图像与卷积以生成更粗糙的分辨率图像。这种方法有一个主要缺点：在粗糙的尺度上准确获取“语义上有意义”的边缘位置很困难。在本文中，我们提出了尺度空间的新定义，并引入了一类利用扩散过程实现此定义的算法。扩散系数的选择在空间上变化，以鼓励区域内平滑而不是区域间平滑。实验证明了常规尺度空间的“在粗糙的尺度上不应生成新的极大值”这一特性得到了保留。由于我们方法中的区域边界保持清晰，我们获得了一个成功利用全局信息的高质量边缘检测器。在多幅图像上展示了实验结果。该算法涉及到在图像上复制的基本局部操作，因此可以实现并行硬件实现。
索引词-自适应滤波，模拟VLSI，边缘检测，边缘增强，非线性扩散，非线性滤波，并行算法，尺度空间。
1.引言
从计算机视觉的早期，例如Rosenfeld和Thurston [20]，人们就开始意识到多尺度描述的重要性。这个问题的一个清晰的形式化方法是由Witkin [21]引入的尺度空间滤波的概念，并在Koenderink [11]，Babaud，Duda和Witkin [1]，Yuille和Poggio [22]以及Hummel [7]，[8]中进行了进一步的发展。这种方法的基本思想非常简单：将原始图像嵌入到一族派生图像I(x,y,t)中，这些图像是通过将原始图像Io(x,y)与方差为t的高斯核G(x,y;t)进行卷积得到的。
较大的尺度空间参数t对应于更粗糙分辨率的图像。请参见图1。正如Koenderink [11]和Hummel [7]所指出的那样，这一参数族的派生图像可以等价地看作是热传导或扩散方程的解。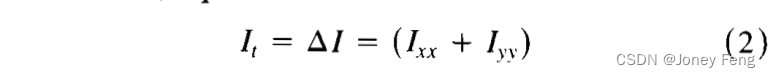
根据Koenderink的论述，扩散方程的公式化是基于两个准则：
1）因果关系：在粗糙的分辨率水平上，任何特征都需要在更细的分辨率水平上具有一个（不一定是唯一的）“原因”，尽管反过来不一定成立。换句话说，当分辨率降低时，不应该产生虚假的细节。
2）均匀性和各向同性：模糊处理需要具有空间不变性。这些准则自然地导致了扩散方程的公式化。值得注意的是，第二个准则仅仅是为了简化而陈述的。稍后我们将对此进行更详细的讨论。事实上，本文的主要主题是用更有用的内容替换这个准则。还应该注意，因果关系准则并不唯一地强制选择高斯进行模糊处理，尽管高斯是最简单的选择。Hummel [7]提出了一个重要的观察结果，即抛物型偏微分方程理论中的最大值原理的一个版本等效于因果关系。我们将在IV-A节中进一步讨论这个问题。本文的结构如下：第二节批评了标准的尺度空间范式，并提出了一组额外的准则来获得“语义上有意义”的多尺度描述。在第三节中，我们展示了通过允许扩散系数的变化可以满足这些准则。在IV-A节中，回顾了最大值原理，并用它来展示我们的方案如何满足因果关系准则。第五节展示了一些实验结果。第六节将我们的方案与其他边缘检测方案进行比较。第七节提出了一些结论性的评论。
图1. 通过将原始的一维信号（底部）与方差从底部到顶部逐渐增大的高斯核进行卷积得到的一族一维信号I(x,t)（改编自Witkin [21]）。
2.标准尺度空间范式的弱点
我们现在要考察标准尺度空间范式在需要"语义上有意义"的多尺度描述的视觉任务中的适用性。自然界中的表面通常具有分层的组织结构，由少量离散的层级组成[13]。在最细的层级上，一棵树由具有复杂脉络结构的叶子组成。在下一层级上，每片叶子被一个单一的区域所取代，而在最高层级上，有一个对应于树顶的单一斑块。每个描述层级都对应着一定的分辨率范围（尺度空间参数的区间）。此外，在每个描述层级上，区域（叶子、树顶或森林）都有明确定义的边界。在标准尺度空间范式中，粗糙尺度上边界的真实位置在粗糙尺度图像中并不直接可用。这在图2的一维示例中可以清楚地看到。粗糙尺度上的边缘位置与其真实位置有所偏移。在二维图像中，还存在另一个问题，即包含边缘绘制的大部分空间信息的边界交叉点被破坏。获取在粗糙尺度上检测到的边缘的真实位置的唯一方法是通过跟踪穿越尺度空间，找到它们在原始图像中的位置。这种技术证明是复杂且昂贵的[5]。
这种空间失真的原因非常明显，高斯模糊并不“尊重”对象的自然边界。假设我们有一张带有天空作为背景的树顶的图片。高斯模糊处理会导致树叶的绿色与天空的蓝色在树顶作为特征出现之前就被“混合”在一起（在树叶被模糊在一起之后）。图3显示了通过高斯模糊得到的一系列较粗的图像，说明了这一现象。还可以注意到，区域边界通常是模糊的，而不是清晰的。基于这一动机，我们提出了生成图像多尺度“语义上有意义”描述的候选范式必须满足的几项标准[18]：
- 因果性：正如Witkin和Koenderink指出的，尺度空间表示应该具有这样的特性，即从较细的尺度到较粗的尺度时不应产生虚假的细节。
- 立即定位：在每个分辨率上，区域边界应该清晰，并与该分辨率上的语义上有意义的边界重合。
- 分段平滑：在所有尺度上，应该优先进行区域内的平滑，而不是区域间的平滑。在前面提到的树的例子中，在与天空背景合并之前，叶子区域应该先被折叠成一个树顶。
图2. 边缘的位置（相对于x的Laplacian的零点）在图1的线性尺度空间中（改编自Witkin [21]）。
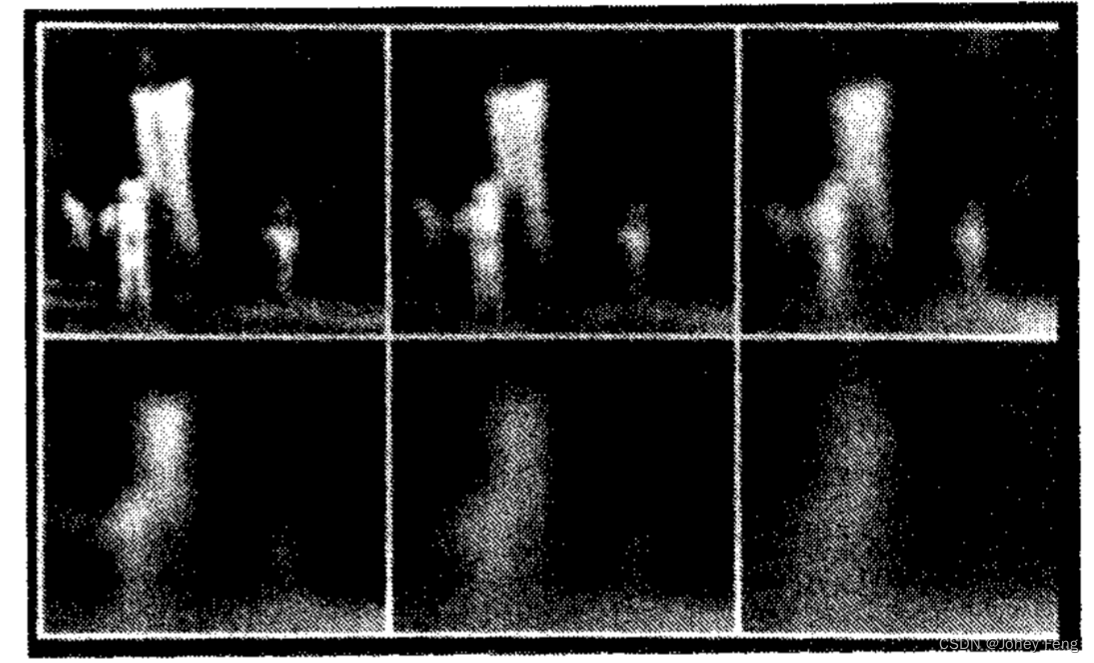图3. 通过各向同性线性扩散（离散8个最近邻实现的0.2.4,8,16,32次迭代）产生的尺度空间（尺度参数从上到下，从左到右递增）。与图12进行比较。
3.各向异性扩散
有一种简单的方法可以修改线性尺度空间范式，以实现我们在前一节中提出的目标。在尺度空间的扩散方程框架中，扩散系数c被假定为与空间位置无关的常数。并没有根本性的理由要求这样。引用Koenderink的话[11, p.3641]：“...我不允许空间变体模糊。显然这对问题并非必要，但它极大地简化了分析。”我们将展示如何选择适当的c(x, y, t)将使我们能够满足前一节中列出的第二和第三个标准。此外，在不牺牲因果性的情况下可以做到这一点。考虑各向异性扩散方程。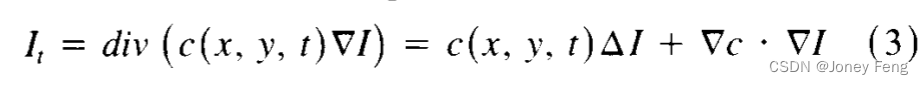
其中，我们用div表示散度算子，用V和A分别表示梯度和拉普拉斯算子，与空间变量相关。如果c(x, y, t)是一个常数，它会简化为各向同性热扩散方程I ,=cAZ。假设在时间（尺度）t上，我们知道适合该尺度的区域边界的位置。我们希望在区域内部而不是跨越边界进行平滑。这可以通过在每个区域内部设置导热系数为1，在边界上设置为0来实现。然后，模糊将在每个区域中单独进行，区域之间没有相互作用。区域边界将保持清晰。当然，我们事先不知道每个尺度上的区域边界（如果我们知道的话，问题已经解决了！）。可以计算的是适合该尺度的边界位置（边缘）的当前最佳估计。设E(x, y, t)是这样一个估计值：一个在图像上定义的矢量值函数，理想情况下应具有以下特性：
1）E(x, y, t)在每个区域的内部为0。
2）E(x, y, t)=Ke(x, y, t)在每个边缘点处，其中e是边缘上的法向量单位，K是边缘的局部对比度（左右图像强度的差异）。需要注意的是，上述中使用的边缘一词并未正式定义-我们在这里指的是感知主观概念中的边缘作为区域边界。一个完全令人满意的正式定义很可能是解决方案的一部分，而不是问题的定义！如果有一个估计值E(x, y, t)，则可以选择导热系数c(x, y, t)为一个关于E的大小的函数c=)IE 11 (x, y, t )g()IE 11 )。根据先前所述的策略，g()必须是一个非负的单调递减函数，且g(0)=1（见图4）。这样，扩散过程主要发生在区域的内部，并且不会影响E的大小较大的区域边界。直观上来说，扩散过程能否满足第II节中的三个尺度空间目标在很大程度上取决于估计E作为边缘位置的“猜测”的准确性。然而，准确性在计算上是昂贵的，需要复杂的算法。我们能够证明，幸运的是，亮度函数的最简单的边缘位置估计，即E(x, y, t)=VZ(x, y, t)，给出了出色的结果。g()有许多可能的选择，最明显的是一个二值函数。在下一节中，我们将展示，如果我们使用边缘估计E(x, y, t)=VZ(x, y, t)，那么g()的选择将受到一类单调递减函数的限制。
图4.非线性函数g(.)的定性形状
4.各向异性扩散的特性
首先，我们通过回顾偏微分方程理论中的一个普遍结果，即最大值原理，来证明各向异性扩散满足第II节的因果性准则。在第IV-B节中，我们将展示，如果扩散中的导热系数被选择为亮度函数梯度的大小的局部函数，即，如果函数g(.)被适当选择，不仅可以保持亮度边缘，还可以使其更加清晰。
A. 最大值原理
因果性准则要求在尺度空间中从细到粗的过程中不引入新的特征。如果我们将图像中的“特征”与亮度函数Z(x, y, t)的“斑点”对应，其中t表示不同尺度参数的值，那么新的“斑点”的出现意味着必须创建一个最大值或最小值，该最大值或最小值要么属于尺度空间的内部，要么属于尺度空间的顶面Z(x, y, tf)（其中tf是尺度空间中最粗的尺度）。因此，通过展示尺度空间中的所有极大值和极小值属于原始图像，可以建立因果性准则。扩散方程（3）是满足最大值原理的更一般类别的椭圆方程的特例。该原理表明，方程在空间和时间上的解的所有极大值都属于初始条件（原始图像）和感兴趣域的边界，前提是传导系数是正的。在我们的情况下，由于我们使用绝热边界条件，最大值原理更加强大：最大值只属于原始图像。关于该原理的证明可以在[17]中找到；为了使本文更完整，我们在附录中提供了一个简单的证明，该证明还涵盖了绝热边界情况，并使用了对传导系数的较弱假设。在第五节中还提出了最大值原理的离散版本。
B. 边缘增强
使用传统的低通滤波和线性扩散来消除噪声和进行尺度空间处理的代价是边缘的模糊。这导致边缘的检测和定位变得困难。这个问题的分析在[4]中给出。通过高通滤波或将扩散方程逆向运行可以实现边缘增强和模糊图像的重建。这是一个不适定问题，并且会导致数值不稳定的计算方法，除非问题被适当约束或重新表述[9]。我们将在这里展示，如果将传导系数选择为图像梯度的适当函数，我们可以使各向异性扩散在时间上向前运行时增强边缘，从而享受到扩散的稳定性，这是由最大值原理所保证的。我们将边缘建模为与高斯卷积的阶跃函数。不失一般性，假设边缘与y轴对齐。散度算子的表达式简化了。
我们选择c为梯度I的函数：c(x, g(I(x, y, t)))。然后扩散方程（3）的一维版本变为y, t) = g(I(x, y, t))，如式（4）所示。让4(z,)表示流量c乘以I。
我们对边缘斜率的时间变化感兴趣：a/at(Z, )。如果c() > 0，函数I()是光滑的，可以颠倒微分的顺序：
假设边缘的方向使得I'>0。在拐点处，I''=0，并且I'''<<0，因为拐点对应于具有最大斜率的点（见图5）。因此，在拐点附近，a/at(Z,)的符号与4r(Z,)相反。如果4r(I,)>0，边缘的斜率将随时间减小；相反，如果4r(I,)<0，斜率将随时间增加。注意，这种斜率的增加不能由边缘的尺度变化引起，因为这将违反最大值原理。边缘变得更加锐利。 有多种可能的4r(.)选择，例如，g(Z,)=C /(1 +(I'/K )'^a)，其中a>0（见图6）。然后存在与K和a相关的阈值，当4r(-)在此阈值以下时，它是单调增加的，而在此阈值以上时，它是单调减少的，从而模糊小的不连续性并使边缘变得更加锐利。还要注意，在边缘最陡峭的区域附近，扩散可以被认为是“倒退运行”，因为(+(I,))在(5)中是负数。这可能是一个令人担忧的问题，因为已知常系数扩散向后运行是不稳定的，并且会放大噪声产生涟漪。但在我们的情况下，这种担忧是没有根据的：最大值原理保证不会产生涟漪。实验观察到，4r(I,)<0的区域迅速缩小，过程保持稳定。
图5：（从上到下）平滑的阶跃边缘及其一阶、二阶和三阶导数。
图6：一种选择的函数4（.），可以实现边缘增强。
5.实验结果
我们使用一个简单的数值方案来测试我们的各向异性扩散、尺度空间和边缘检测思想，该方案在本节中描述。方程（3）可以在一个方形网格上离散化，亮度值与顶点相关联，传导系数与弧相关联（见图7）。可以使用4个最近邻的离散化Laplacian算子：
其中0 <= IX <= 1/4是为了使数值方案稳定，N、S、E、W是北、南、东、西的助记符下标，方括号上的上标和下标应用于其包含的所有项，并且符号V（不要与我们用于梯度算子的V混淆）表示最近邻的差异：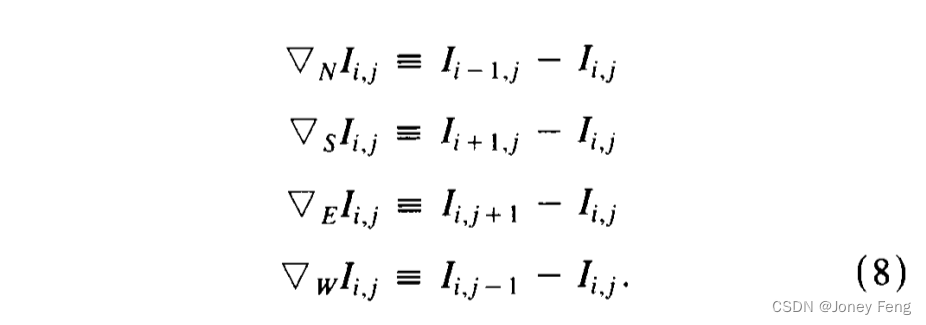
传导系数在每次迭代中根据亮度梯度（4）进行更新：
梯度的值可以在不同的邻域结构上进行计算，从而在准确性和局部性之间实现不同的平衡。最简单的选择是在每个弧位置上用其沿弧方向投影的绝对值来近似梯度的范数：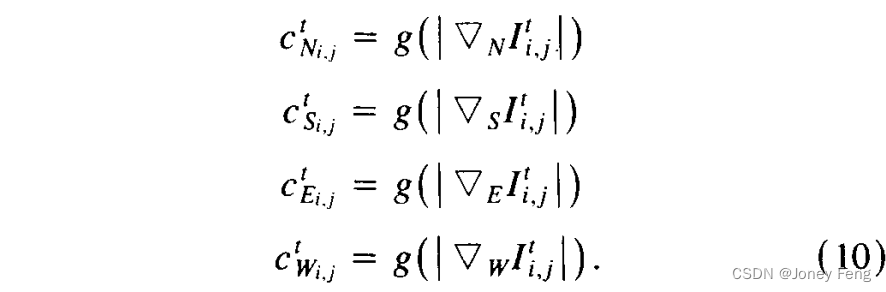
该方案并不是对方程（3）的精确离散化，而是对类似扩散方程的离散化，其中传导张量是对角矩阵，其条目为g（I I1）和g（I Iy1），而不是g（I I11）和g（I IIV1）。这种离散化方案保持了连续方程（3）中亮度总量不变的性质。此外，图像中每个弧的亮度“通量”仅取决于定义它的两个节点的亮度值，这使得该方案成为模拟VLSI实现的自然选择[19]。见图8。更精细的梯度近似可以产生感知上类似的结果，但计算复杂度增加。
可以验证，无论梯度的近似选择如何，离散化方案仍然满足最大（和最小）原则，前提是函数g在0和1之间有界。事实上，我们可以直接从（7）中证明这一点，使用事实：X E [0,1/4]和c E [0,1]，并定义（I M ）= max {(I, IN, IS, IE, IW)}和（I m ）= min {(I, IN, IS, IE, IW)}，即Z在迭代t中的邻居的最大和最小值。我们可以证明：
即，在离散化的尺度空间的内部不可能存在（局部）最大值和最小值。实际上：
本文中用于生成图片的数值方案是由方程（7），（8）和（10）给出的方案，使用原始图像作为初始条件，并使用绝热边界条件，即将传导系数在图像边界处设为零。传导系数c的常数值（即g（*）= 1）会导致高斯模糊（见图3）。使用不同的g（-）函数可以得到感知上相似的结果。本文中的图像是使用...获得的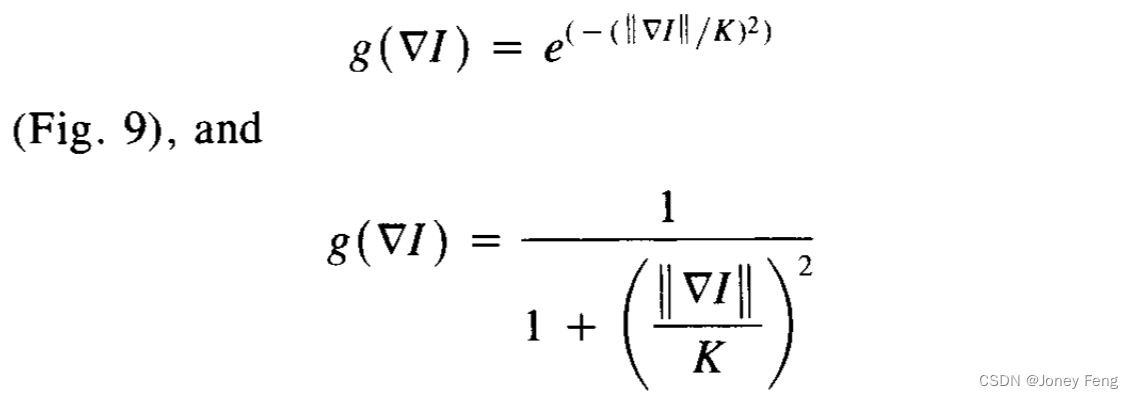
（图12-14）。这两个函数生成的尺度空间是不同的：第一个更看重高对比度的边缘而不是低对比度的边缘，第二个更看重较大的区域而不是较小的区域。常数K要么通过手动设置为固定值（见图9-14），要么使用Canny [4]描述的“噪声估计器”进行设置：计算整个图像中梯度的绝对值的直方图，并在每次迭代中将K设置为其积分的90％值（见图12（b））。本节中描述的计算方案之所以选择是因为它的简单性。其他扩散方程的数值解和多尺度算法可以考虑用于高效的软件实现。
图7.模拟扩散方程的离散计算方案的结构（有关物理实现，请参见图8）。亮度值I与一个点阵的节点相关联，传导系数c与弧相关联。图示了一个节点及其四个北、东、西、南邻居。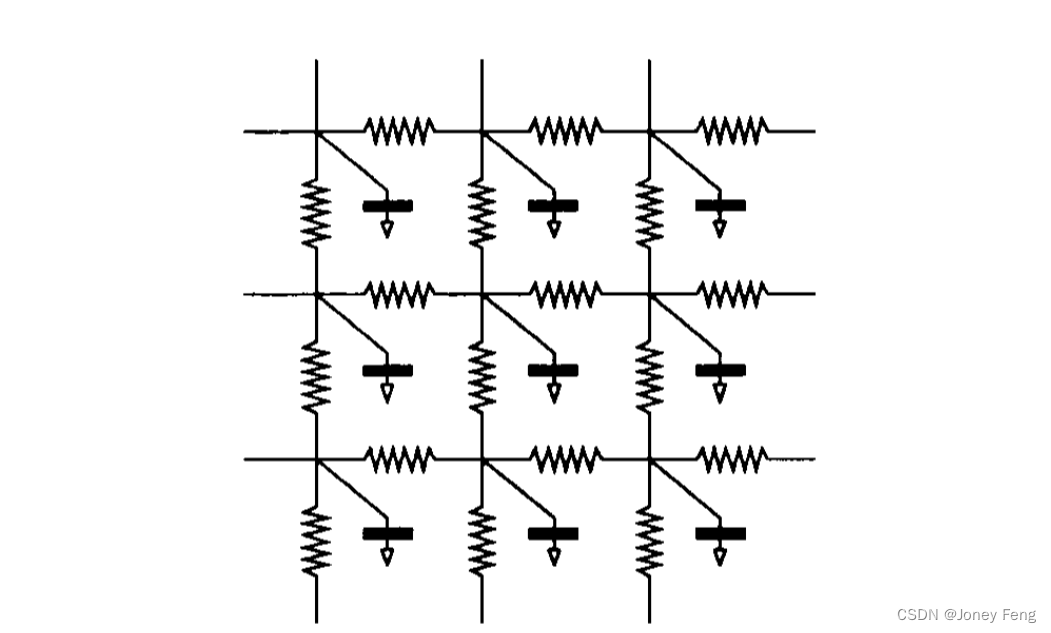
图8.实现在第V节中描述的各向异性扩散的网络结构，更详细的说明请参见[19]。网络中每个节点上的电容电荷代表像素处图像的亮度。线性电阻产生各向同性的线性扩散。具有如图6所示I-V特性的电阻产生各向同性扩散。
图9.各向异性扩散（b）对Canaletto图像（a）的影响[3]。
6.与其他边界检测方法比较
本节将比较我们在本文中提出的各向异性扩散方案与先前关于边缘检测、图像分割和图像恢复的工作。我们将边缘检测器分为两类：固定邻域边缘检测器和能量/概率“全局”方案。
A.固定邻域检测器
这类边缘检测器仅使用局部信息-它们通常检查图像的一个小窗口，并尝试智能地确定是否存在边缘以及在哪里存在边缘。这种决策是模糊且困难的。我们选择Canny的方案[4]作为这类边缘检测器的代表。该方案使用高斯的方向导数与图像进行卷积-其思想是沿着边缘进行平滑，从而在不过渡模糊边缘的情况下减少噪声。但是，存在两个主要困难：1）使用线性滤波器会导致局部化精度与可检测性之间的不可避免的权衡；2）在多尺度上组合滤波器的输出的复杂性。各向异性扩散是一个非线性过程，因此原则上不受限制1)的限制。通过局部自适应平滑，避免了多尺度、多方向滤波器的复杂性。因此，我们可以总结出我们提出的方案相比于线性固定邻域边缘检测器的优势。 局部性：平滑发生的邻域的形状和大小由图像的亮度模式在局部确定，并且根据需要平滑的区域的形状和大小进行自适应。在基于线性平滑或固定邻域处理的方案中，平滑发生的区域的形状和大小在整个图像中是恒定的。这会导致有意义的区域形状的扭曲，并且丢失像边缘交叉点（见图10(b)、12(d)、15）这样的结构，这些结构包含了允许对边缘线绘制进行三维解释的大部分信息[121]。
Simplicig算法是在4（8）连接的正方形格点上迭代进行相同的最近邻操作（4-8个差异、一个函数评估或表查找以及4-8个求和）的算法。相比之下，Canny边缘检测器需要一系列的卷积（每次涉及大邻域）作为预处理阶段，并且需要一个跨尺度匹配阶段。此外，我们的算法通过第四节讨论的扩散过程使边缘变得锐利，因此边缘细化和连接几乎是不必要的，尤其是在粗糙分辨率的情况下（将图17与图16进行比较）。对于基于卷积的边缘检测器来说，这是一个必要、精细且昂贵的步骤，因为线性低通滤波会模糊边缘。各向异性扩散中涉及的计算的简单性使其成为数字硬件实现的良好选择。并行性：算法的结构是并行的，这使得它在简单并行处理器阵列上运行成本较低。在顺序机器上，各向异性扩散的计算成本比基于卷积的检测器更高。这是因为在扩散过程中生成了一系列连续的尺度，而不是一个小固定数量的尺度。
B.基于能量的图像重建和分割方法
文献中出现了许多方法，其中边缘检测和图像分割过程是通过最小化一种能量函数来实现的。
其中，Z表示格点的集合，N(i)表示与节点i相邻的节点集合，z是定义在格点上的函数，通常是亮度函数[2]。另一种等价的表述是基于在所有图像空间上定义的马尔可夫概率分布函数的最大值的寻找。
函数U(*)具有(14)[6],[14]的形式。由于指数函数是单调的，概率分布的最大值和能量函数的最小值是相同的，因此我们可以将注意力限制在基于能量最小化的方案上。能量函数(14)由两个项的和组成：先验项（包含关于图像空间的先验知识的“团”函数V的和，详见[6]、[16]、[2]中的任意一篇文章进行完整讨论），以及依赖于可用数据的项（函数Wi的和）。V(e, *)通常是一个偶函数，仅取决于其参数差值的值（滥用符号表示V(zi, zj) = V(zj - zi)）。它在零处取得最小值，并且在正负半线上是单调的，将更高的能量（更低的概率）分配给亮度差异大的格点对i，j。我们将展示在第五节中建议的各向异性扩散的近似可以看作是能量函数先验部分的梯度下降。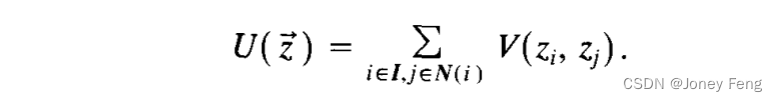
寻找函数最小值的最速下降策略包括从某个初始状态开始，然后迭代地根据梯度向量的相反方向改变状态。能量函数的梯度可以从(16)中对zi求导得到，它是分量的向量。因此，梯度下降算法是这
样的。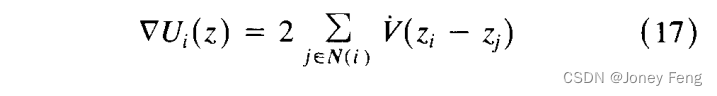
其中A是某个“速度”因子。假设V(-)在原点可导，并且定义k g define+(.)=-k，由于V(.)是偶函数，+(.)是奇函数，且+(0)=0。然后我们可以写成+(s)=s c(s)，其中c()是一个偶且正的函数。将其代入(18)中，我们得到。
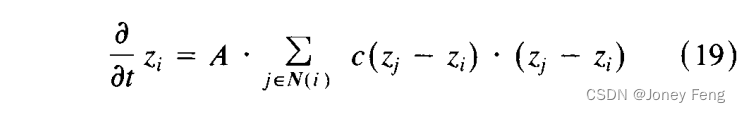这正是由方程(7)、(8)和(10)定义的各向异性扩散算法，如果邻域结构由方形格点的最近邻团组成。由[6]、[15]、[2]中的局部能量函数V()求导得到的流函数与第四节-B中的分析所建议的流函数的形状相似。见图18。总结一下：各向异性扩散可以看作是对某个能量函数的梯度下降。数据（原始图像）被用作初始条件。在基于能量的方法[6]、[16]、[2]中，通过能量函数中的一个项来强制解对数据的闭合性。这使得能量函数非凸，并且需要比梯度下降更复杂的优化算法。大多数已经提出的算法（例如模拟退火）对于视觉应用来说速度太慢。也许唯一的例外是Blake和Zisserman提出的GNC算法[2]，它不能保证对于一般图像找到全局最优解，但在速度和准确性之间取得了良好的折衷。
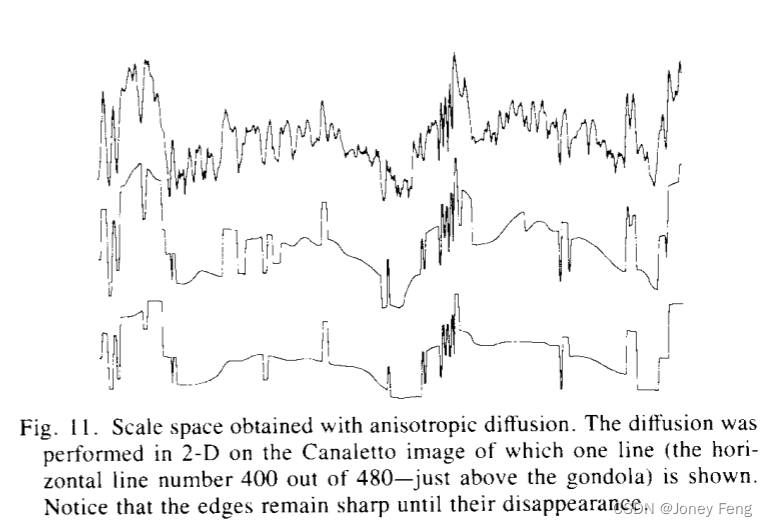
图12。从左到右：（a）原始图像，（b）使用各向同性扩散的尺度空间（10.20.80次迭代），（c）相同图像的边缘，（d）使用Canny边缘检测器检测到的可比较尺度的边缘（卷积核方差为1.2.4像素）。
图13。使用各向异性扩散的尺度空间。图12中亮度的三维图（a）原始图像（b）经过各向异性扩散平滑后。
图14。使用各向异性扩散的尺度空间。原始图像（左上方）和经过（从左到右，从上到下）20、60、120、160、220、280、320、400次迭代后的粗略尺度图像。
图15。使用线性卷积的尺度空间。边缘被扭曲，交叉点消失。使用Canny边缘检测器和方差为1/2、1、2、4、8、16像素的平滑高斯核生成的图像。（与图17相比，各向异性扩散保留了边缘的交叉点、形状和位置）
图16。使用阈值处理梯度在图14中检测到的边缘。不需要连接。细化仅适用于较细的尺度。与使用细化和连接的图17相比。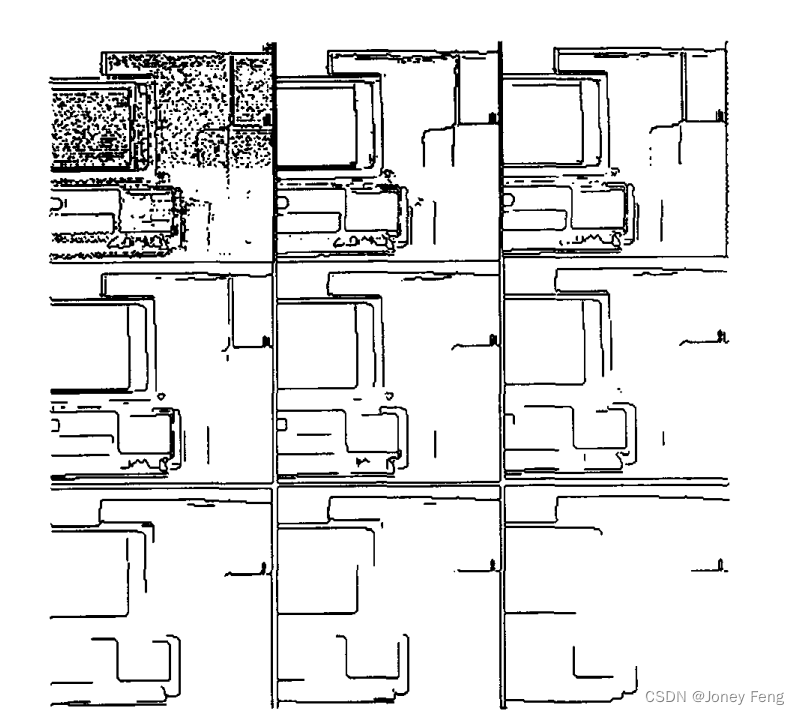
图17。使用细化和连接阶段在图14中检测到的边缘。
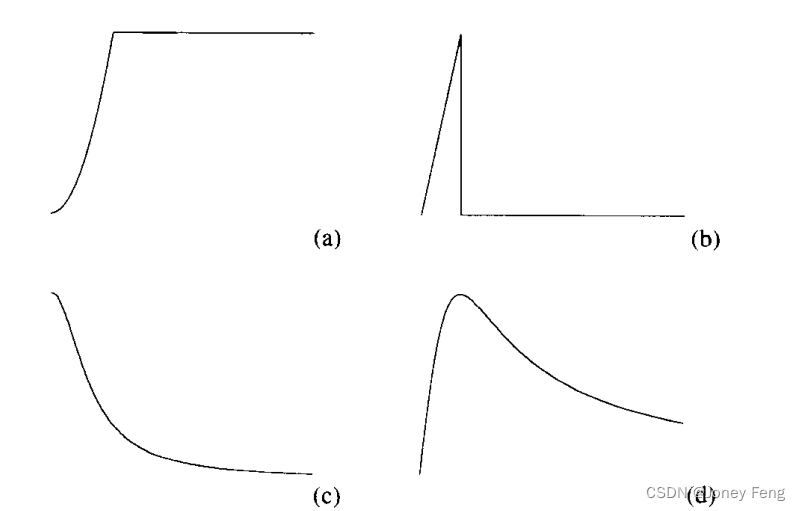图18。（a）由[6]、[2]、[14]提出的局部能量函数通常等于最近邻亮度差的平方，并在某个阈值处饱和。（b）能量函数（a）的一阶导数。（c）和（d）各向异性扩散传导系数和流函数，作为亮度梯度大小的函数，与离散情况下的最近邻亮度差成比例。（b）和（d）具有相同的作用。
7.总结
我们介绍了一种工具，各向异性扩散，我们相信它在早期视觉的许多任务中将证明其有用性。基于扩散的算法涉及整个图像格点上的简单、局部、相同的计算。在像连接机这样的大规模并行架构上实现几乎是微不足道的。使用混合模拟-数字网络的实现也似乎是可行的。我们已经证明，最简单的各向异性扩散版本可以成功地应用于多尺度图像分割。作为预处理步骤，它使得细化和连接边缘变得不必要，保留了边缘交叉点，并且不需要在不同尺度上对图像进行复杂的比较，因为形状和位置在每个尺度上都得到保留。在亮度梯度由噪声产生的图像中，如果噪声的梯度大于边缘的梯度，并且噪声水平在图像中变化显著，我们所描述的方案无法获得正确的多尺度分割。在这种情况下，全局噪声估计不能提供准确的局部估计，而梯度的局部值提供的信息对于区分与噪声相关和与边缘相关的梯度过于局限。此外，流函数的峰值的横坐标K必须根据典型的对比度值进行设置，如果这个值在整个图像中变化很大，那么K的值必须在局部进行设置。为了解决这些困难，应该使用局部对比度和噪声估计来实现各向异性扩散。
8.参考文献
[l] J.Babaud, A.Witkin, M.Baudin和R.Duda，“尺度空间滤波中高斯核的唯一性”，IEEE Trans.Pattern Anal.Machine Intell.，vol.PAMI-8，1986年1月。
[2] A.Blake和A.Zisserman，“视觉重建”，剑桥，MA：MIT Press，1987年。
[3] Canaletto，“威尼斯的风景”，美国国家艺术馆，华盛顿特区，约1740年。
[4] J.Canny，“边缘检测的计算方法”，IEEE Trans.Pattern Anal.Machine Intell.，vol.PAMI-8，1986年，pp.679-698。
[5] J.Clark，“尺度空间中奇点理论和幻影边缘”，IEEE Trans.Pattern Anal.Machine Intell.，vol.10，no.5，1988年，pp.720-727。
[6] S.Geman和D.Gernan，“随机松弛，Gibbs分布和贝叶斯图像恢复”，IEEE Trans.Pattern Anal.Machine Intell.，vol.PAMI-6，1984年，pp.721-741。
[7] A.Huminel，“基于零交叉的尺度空间表示”，在Proc.IEEE计算机视觉和模式识别会议上，1986年6月，pp.204-209：在《计算机视觉读物》中再现：M.Fischler和0.Firschein，编者，计算机视觉：问题，原理和方法，第181页。
[8] “金字塔数据结构的尺度空间形式”，在Parallel Computer Vision中，L.Uhr，编者，纽约：Academic Press，1987年。
[9] A.Hummel，B.Kimia和S.Zucker，“去模糊高斯模糊”，计算机视觉，图形和图像处理，vol.38，1987年，pp.66-80。
[10] F.John，“偏微分方程”，纽约：Springer-Verlag，1982年。
[11] J.Koenderink，“图像的结构”，生物控制，vol.50。
[12] J.Malik，“解释弯曲对象的线条绘图”，国际纯粹与应用数学杂志。
[13] D.Marr，“视觉”，洛杉矶，CA：Freeman，1982年。
[14] J.Marroquin，“逆问题的概率解决方案”，博士论文，麻省理工学院，1985年。
[15] “逆问题的概率解决方案”，人工智能实验室，麻省理工学院，技术报告AI-TR 860，1985年。
[16] D.Mumford和J.Shah，“分段光滑函数的最优逼近及相关变分问题”，Commun.Pure Appl.Math.，vol.42，1989年，pp.577-685。
[17] L.Nirenharg，“抛物方程的强最大原理”，Commuri.Purr Appl.Math.，vol.VI，1953年，pp.167-177。
[18] P.Perona和J.Malik，“使用各向同性扩散的尺度空间和边缘检测”，在Proc.IEEE计算机协会视觉会议上，1987年，pp.16-27。
[19] “一个用于边缘检测和尺度空间的网络”，在Proc.IEEE国际博览会上，1988年，pp.2565-2568。
[20] A.Rosenfeld和M.Thurston，“用于视觉场景分析的边缘和曲线检测”，IEEE Trans.Compur.，vol.C-20，1971年5月，pp.562-569。
[21] Los Altos，CA：Morgan Kaufmann，1987年，pp.187-223。
[22] Compur.Vision，vol.I，no.I，1982年，pp.73-103。
[23] A.Witkin，“尺度空间滤波”，在国际人工智能会议上，卡尔斯鲁厄，西德，1983年，pp.1019-1021。
[24] A.Yuille和T.Poggio，“零交叉的尺度定理”，IEEE Trans.Pattern Anal.Machine Intell.，vol.PAMI-8，1986年1月。