[PaddlePaddle] [学习笔记] PaddlePaddle 官方文档 —— ①使用Python和NumPy构建神经网络模型；②使用PaddlePaddle预测波士顿房价

1. 机器学习和深度学习综述

1.1 人工智能、机器学习、深度学习的关系

近些年人工智能、机器学习和深度学习的概念十分火热，但很多从业者却很难说清它们之间的关系，外行人更是雾里看花。在研究深度学习之前，先从三个概念的正本清源开始。概括来说，人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的，三者的关系如下图所示，即：人工智能 > 机器学习 > 深度学习。

人工智能（Artificial Intelligence，AI）是最宽泛的概念，是研发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。由于这个定义只阐述了目标，而没有限定方法，因此实现人工智能存在的诸多方法和分支，导致其变成一个“大杂烩”式的学科。机器学习（Machine Learning，ML）是当前比较有效的一种实现人工智能的方式。深度学习（Deep Learning，DL）是机器学习算法中最热门的一个分支，近些年取得了显著的进展，并替代了大多数传统机器学习算法。

1.2 机器学习

区别于人工智能，机器学习、尤其是监督学习则有更加明确的指代。机器学习是专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构，使之不断改善自身的性能。这句话有点“云山雾罩”的感觉，让人不知所云，下面我们从机器学习的实现和方法论两个维度进行剖析，帮助读者更加清晰地认识机器学习的来龙去脉。

1.2.1 机器学习的实现

机器学习的实现可以分成两步：①训练和②预测，类似于归纳和演绎：

• 归纳： 从具体案例中抽象一般规律，机器学习中的“训练”亦是如此。从一定数量的样本（已知模型输入 $X$ 和模型输出 $Y$）中，学习输出 $Y$ 与输入 $X$ 的关系（可以想象成是某种表达式）。

• 演绎： 从一般规律推导出具体案例的结果，机器学习中的“预测”亦是如此。基于训练得到的 $Y$ 与 $X$ 之间的关系，如出现新的输入 $X$，计算出输出 $Y$。通常情况下，如果通过模型计算的输出和真实场景的输出一致，则说明模型是有效的。

1.2.2 机器学习的方法论

机器学习的方法论和人类科研的过程有着异曲同工之妙，下面以“机器从牛顿第二定律实验中学习知识”为例，帮助读者更加深入理解机器学习（监督学习）的方法论本质，即在“机器思考”的过程中确定模型的三个关键要素：

1. 假设
2. 评价
3. 优化

1.2.2.1 案例：机器从牛顿第二定律实验中学习知识

牛顿第二定律是艾萨克·牛顿在1687年于《自然哲学的数学原理》一书中提出的，其常见表述：物体加速度的大小跟作用力成正比，跟物体的质量成反比，与物体质量的倒数成正比。牛顿第二运动定律和第一、第三定律共同组成了牛顿运动定律，阐述了经典力学中基本的运动规律。

在中学课本中，牛顿第二定律有两种实验设计方法：①倾斜滑动法和②水平拉线法，如图所示。

相信很多读者都有摆弄滑轮和小木块做物理实验的青涩年代和美好回忆。通过多次实验数据，可以统计出如下表所示的不同作用力下的木块加速度。

次数	作用力 $X$	加速度 $Y$
1	4	2
2	4	2
…	…	…
n	6	3

观察实验数据不难猜测，物体的加速度 $a$ 和作用力 $F$ 之间的关系应该是线性关系。因此我们提出假设 $a=w\cdot F$，其中，$a$ 代表加速度，$F$ 代表作用力，$w$ 是待确定的参数。

通过大量实验数据的训练，确定参数 $w$ 是物体质量的倒数 $\frac{1}{m}$，即得到完整的模型公式 $a=F\cdot \frac{1}{m}$。当已知作用到某个物体的力时，基于模型可以快速预测物体的加速度。例如：燃料对火箭的推力 $F=10$，火箭的质量 $m=2$，可快速得出火箭的加速度 $a=5$。

1.2.2.2 如何确定模型参数？

这个有趣的案例演示了机器学习的基本过程，但其中有一个关键点的实现尚不清晰，即：如何确定模型参数 $w=\frac{1}{m}$？

确定参数的过程与科学家提出假说的方式类似，合理的假说可以最大化的解释所有的已知观测数据。如果未来观测到不符合理论假说的新数据，科学家会尝试提出新的假说。如：天文史上，使用大圆和小圆组合的方式计算天体运行，在中世纪是可以拟合观测数据的。但随着欧洲工业革命的推动，天文观测设备逐渐强大，已有的理论已经无法解释越来越多的观测数据，这促进了使用椭圆计算天体运行的理论假说出现。因此，模型有效的基本条件是能够拟合已知的样本，这给我们提供了学习有效模型的实现方案。

上图是以 $H$ 为模型的假设，它是一个关于参数 $w$ 和输入 $x$ 的函数，用 $H(w,x)$ 表示。模型的优化目标是 $H(w,x)$ 的输出与真实输出 $Y$ 尽量一致，两者的相差程度即是模型效果的评价函数（相差越小越好）。

那么，确定参数的过程就是在已知的样本上，不断减小该评价函数（$H$ 和 $Y$ 的差距）的过程。直到模型学习到一个参数 $w$，使得评价函数的值最小，衡量模型预测值和真实值差距的评价函数也被称为损失函数（损失Loss）。

假设机器通过尝试答对（最小化损失）大量的习题（已知样本）来学习知识（模型参数 $w$），并期望用学习到的知识所代表的模型 $H(w,x)$，回答不知道答案的考试题（未知样本）。最小化损失是模型的优化目标，实现损失最小化的方法称为优化算法，也称为寻解算法（找到使得损失函数最小的参数解）。参数 $w$ 和输入 $x$ 组成公式的基本结构称为假设。在牛顿第二定律的案例中，基于对数据的观测，我们提出了线性假设，即作用力和加速度是线性关系，用线性方程表示。由此可见，①模型假设、②评价函数（损失/优化目标）和③优化算法 是构成模型的三个关键要素。

1.2.2.3 模型结构

模型假设、评价函数和优化算法是如何支撑机器学习流程的呢？如下图所示。

• 模型假设：世界上的可能关系千千万，漫无目标的试探 $Y\leftarrow X$ 之间的关系显然是十分低效的。因此假设空间先圈定了一个模型能够表达的关系可能，如蓝色圆圈所示。机器还会进一步在假设圈定的圆圈内寻找最优的 $Y\leftarrow X$ 关系，即确定参数 $w$。
• 评价函数：寻找最优之前，我们需要先定义什么是最优，即评价一个 $Y\leftarrow X$ 关系的好坏的指标。通常衡量该关系是否能很好的拟合现有观测样本，将拟合的误差最小作为优化目标。
• 优化算法：设置了评价指标后，就可以在假设圈定的范围内，将使得评价指标最优（损失函数最小/最拟合已有观测样本）的 $Y\leftarrow X$ 关系找出来，这个寻找最优解的方法即为优化算法。最笨的优化算法即按照参数的可能，穷举每一个可能取值来计算损失函数，保留使得损失函数最小的参数作为最终结果。

从上述过程可以得出，机器学习的过程与牛顿第二定律的学习过程基本一致，都分为 假设、评价和 优化 三个阶段：

• 假设：通过观察加速度 $a$ 和作用力 $F$ 的观测数据，假设 $a$ 和 $F$是线性关系，即 $a=w\cdot F$。
• 评价：对已知观测数据上的拟合效果好，即 $w\cdot F$ 计算的结果要和观测的 $a$ 尽量接近。
• 优化：在参数 $w$ 的所有可能取值中，发现 $w=\frac{1}{m}$ 可使得评价最好（最拟合观测样本）。

机器执行学习任务的框架体现了其学习的本质是“参数估计”（Learning is parameter estimation）。

上述方法论使用更规范化的表示如下图所示，未知目标函数 $f$，以训练样本 $D=(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$ 为依据。从假设集合 $H$ 中，通过学习算法 $A$ 找到一个函数 $g$。如果 $g$ 能够最大程度的拟合训练样本 $D$，那么可以认为函数 $g$ 就接近于目标函数 $f$。

在此基础上，许多看起来完全不一样的问题都可以使用同样的框架进行学习，如科学定律、图像识别、机器翻译和自动问答等，它们的学习目标都是拟合一个“大公式 $f$”，如下图所示。

1.3 深度学习

机器学习算法理论在上个世纪 90 年代发展成熟，在许多领域都取得了成功，但平静的日子只延续到 2010 年左右。随着大数据的涌现和计算机算力提升，深度学习模型异军突起，极大改变了机器学习的应用格局。今天，多数机器学习任务都可以使用深度学习模型解决，尤其在语音、计算机视觉和自然语言处理等领域，深度学习模型的效果比传统机器学习算法有显著提升。

相比传统的机器学习算法，深度学习做出了哪些改进呢？其实两者在理论结构上是一致的，即：模型假设、评价函数和优化算法，其根本差别在于假设的复杂度。如上图第二个示例（图像识别）所示，对于美女照片，人脑可以接收到五颜六色的光学信号，能快速反应出这张图片是一位美女。但对计算机而言，只能接收到一个数字矩阵，对于美女这种高级的语义概念，从像素到高级语义概念中间要经历的信息变换的复杂性是难以想象的，这个转换的过程如下图所示。

这种变换已经无法用数学公式表达，因此研究者们借鉴了人脑神经元的结构，设计出神经网络的模型，如下图所示。

图（a）展示了神经网络基本单元 —— 感知机（Perception）的设计方案，其处理信息的方式与人脑中的单一神经元有很强的相似性；图（b）展示了几种经典的神经网络结构（后续的章节中会详细阐述），类似于人脑中多种基于大量神经元连接而形成的不同职能的器官。

1.3.1 神经网络的基本概念

人工神经网络包括多个神经网络层，如：卷积层（Convolution Layer）、全连接层（Fully Connected Layer）、LSTM（Long Short-Term Memory，长短期记忆网络）等，每一层又包括很多神经元（neuron），超过三层的非线性神经网络都可以被称为深度神经网络（D-CNN）。通俗的讲，深度学习的模型可以视为是输入到输出的映射函数，如图像到高级语义（美女）的映射，足够深的神经网络理论上可以拟合任何复杂的函数。因此神经网络非常适合学习样本数据的内在规律和表示层次，对文字、图像和语音任务有很好的适用性。这几个领域的任务是人工智能的基础模块，因此深度学习被称为实现人工智能的基础也就不足为奇了。神经网络（NN）基本结构如下图所示。

其中：

• 神经元（neuron）： 神经网络中每个节点称为神经元，由两部分组成：
  1. 加权和：将所有输入加权求和。
  2. 非线性变换（激活函数）：加权和的结果经过一个非线性函数变换，让神经元计算具备非线性的能力。
• 多层连接： 大量这样的节点按照不同的层次排布，形成多层的结构连接起来，即称为神经网络。
• 前向计算： 从输入计算输出的过程，顺序从网络前至后。
• 计算图： 以图形化的方式展现神经网络的计算逻辑又称为计算图，也可以将神经网络的计算图以公式的方式表达：$$Y=f_3(f_2(f_1(w_1\cdot x_1+w_2\cdot x_2+w_3\cdot x_3+b)+...)+...)$$

由此可见，神经网络（NN）并没有那么神秘，它的本质是一个含有很多参数的“大公式”。

1.3.2 深度学习的发展历程

神经网络思想的提出已经是 70 多年前的事情了，现今的神经网络和深度学习的设计理论是一步步趋于完善的。在这漫长的发展岁月中，一些取得关键突破的闪光时刻，值得深度学习爱好者们铭记，如 下图所示。

• 1940 年代：首次提出神经元的结构，但权重是不可学的。
• 50-60 年代：提出权重学习理论，神经元（Neuron）结构趋于完善，开启了神经网络（NN）的第一个黄金时代。
• 1969 年：提出异或（XOR）问题（人们惊讶的发现神经网络模型连简单的异或问题也无法解决，对其的期望从云端跌落到谷底），神经网络模型进入了被束之高阁的黑暗时代。
• 1986 年：新提出的多层神经网络解决了异或问题，但随着 90 年代后理论更完备并且实践效果更好的 SVM 等机器学习模型的兴起，神经网络并未得到重视。
• 2010 年左右：深度学习进入真正兴起时期。随着神经网络模型改进的技术在语音和计算机视觉任务上大放异彩，也逐渐被证明在更多的任务，如自然语言处理（NLP）以及海量数据的任务上更加有效。至此，神经网络模型重新焕发生机，并有了一个更加响亮的名字：深度学习（Deep Learning）。

为何神经网络到 2010 年后才焕发生机呢？这与深度学习成功所依赖的先决条件：①大数据涌现、②硬件发展和③算法优化有关。

1. 大数据涌现：大数据是神经网络发展的有效前提。神经网络（NN）和深度学习（DL）是非常强大的模型，需要足够量级的训练数据。时至今日，之所以很多传统机器学习算法和人工特征依然是足够有效的方案，原因在于很多场景下没有足够的标记数据来支撑深度学习。深度学习的能力特别像科学家阿基米德的豪言壮语：“给我一根足够长的杠杆，我能撬动地球！”。深度学习也可以发出类似的豪言：“给我足够多的数据，我能够学习任何复杂的关系”。但在现实中，足够长的杠杆与足够多的数据一样，往往只能是一种美好的愿景。直到近些年，各行业 IT 化程度提高，累积的数据量爆发式地增长，才使得应用深度学习模型成为可能。
2. 硬件发展和算法优化：依靠硬件的发展和算法的优化。现阶段，依靠更强大的计算机、GPU、autoencoder 预训练和并行计算等技术，深度学习在模型训练上的困难已经被逐渐克服。其中，数据量和硬件是更主要的原因。没有前两者，科学家们想优化算法都无从进行。

1.3.3 深度学习的研究和应用蓬勃发展

早在 1998 年，一些科学家就已经使用神经网络模型识别手写数字图像（MNIST）了。但深度学习在计算机视觉应用上的兴起，还是在 2012 年 ImageNet 比赛上，使用 AlexNet 做图像分类。如果比较下 1998 年和 2012 年的模型，会发现两者在网络结构上非常类似，仅在细节上有所优化。在这 14 年间，计算性能的大幅提升和数据量的爆发式增长，促使模型完成了从“简单的数字识别”到“复杂的图像分类”的跨越。

虽然历史悠久，但深度学习在今天依然在蓬勃发展，一方面基础研究快速发展，另一方面工业实践层出不穷。基于深度学习的顶级会议 ICLR(International Conference on Learning Representations) 统计，深度学习相关的论文数量呈逐年递增的状态，如下图所示。同时，不仅仅是深度学习会议，与数据和模型技术相关的会议 ICML 和 KDD，专注视觉的 CVPR 和专注自然语言处理的 EMNLP 等国际会议的大量论文均涉及着深度学习技术。该领域和相关领域的研究方兴未艾，技术仍在不断创新突破中。

另一方面，以深度学习为基础的人工智能技术，在升级改造众多的传统行业领域，存在极其广阔的应用场景。下图选自艾瑞咨询的研究报告，人工智能技术不仅可在众多行业中落地应用（广度），同时，在部分行业（如安防、遥感、互联网、金融、工业等）已经实现了市场化变现和高速增长（深度），为社会贡献了巨大的经济价值。

如下图所示，以计算机视觉（CV）的行业应用分布为例，根据 IDC 的数据统计和预测，随着人工智能向各个行业的渗透，当前较多运用人工智能的互联网行业的产值占比反而会逐渐变小。

1.3.4 深度学习改变了 AI 应用的研发模式

1.3.4.1 实现了端到端（End2End）的学习

深度学习改变了很多领域算法的实现模式。在深度学习兴起之前，很多领域建模的思路是投入大量精力做特征工程，将专家对某个领域的“人工理解”沉淀成特征表达，然后使用简单模型完成任务（如分类或回归）。而在数据充足的情况下，深度学习模型可以实现端到端（End2End）的学习，即不需要专门做特征工程，将原始的特征输入模型中，模型可同时完成特征提取和分类任务，如下图所示。

以计算机视觉任务为例，特征工程是诸多图像科学家基于人类对视觉理论的理解，设计出来的一系列提取特征的计算步骤，典型如 SIFT 特征。在 2010 年之前的计算机视觉领域，人们普遍使用 SIFT 一类特征 + SVM 一类的简单浅层模型完成建模任务。

说明：

1. SIFT 特征由 David Lowe 在 1999 年提出，在 2004 年加以完善。SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用 SIFT 特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要 3 个以上的 SIFT 物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT 特征的信息量大，适合在海量数据库中快速准确匹配。

2. 深度学习和传统机器学习最本质的区别在于特征工程的需求：

   • 在传统机器学习中，特征工程是一个重要的步骤，需要领域专家手动从原始数据中设计和选择相关的特征，作为输入供机器学习算法使用。这个过程通常需要大量领域知识、数据预处理和人工努力来创建信息丰富、有意义的数据表示。
   • 而深度学习则能够在训练过程中自动地从原始数据中学习到相关特征。深度学习模型，尤其是神经网络，能够通过多个计算层次逐渐学习到数据的层次化表示。这种自动学习特征的能力使得深度学习更加适用于处理复杂和高维数据。

1.3.4.2 实现了深度学习框架标准化

除了应用广泛的特点外，深度学习还推动人工智能进入工业大生产阶段，算法的通用性导致标准化、自动化和模块化的框架产生，如下图 所示。

在此之前，不同流派的机器学习算法理论和实现均不同，导致每个算法均要独立实现，如随机森林（RF）和支撑向量机（SVM）。但在深度学习框架下，不同模型的算法结构有较大的通用性，如常用于计算机视觉的卷积神经网络模型（CNN）和常用于自然语言处理的长期短期记忆模型（LSTM），都可以分为组网模块、梯度下降的优化模块和预测模块等。这使得抽象出统一的框架成为了可能，并大大降低了编写建模代码的成本。一些相对通用的模块，如网络基础算子的实现、各种优化算法等都可以由框架实现。建模者只需要关注数据处理，配置组网的方式，以及用少量代码串起训练和预测的流程即可。

在深度学习框架出现之前，机器学习工程师处于“手工作坊”生产的时代。为了完成建模，工程师需要储备大量数学知识，并为特征工程工作积累大量行业知识。每个模型是极其个性化的，建模者如同手工业者一样，将自己的积累形成模型的“个性化签名”。而今，“深度学习工程师”进入了工业化大生产时代，只要掌握深度学习必要但少量的理论知识，掌握 Python 编程，即可在深度学习框架上实现非常有效的模型，甚至与该领域最领先的模型不相上下。建模领域的技术壁垒面临着颠覆，也是新入行者的机遇。

1.4 人工智能的职业发展空间广阔

下面就从经济回报的视角，分析下人工智能是不是一个有前途的职业。坦率的说，如巴菲特所言，选择一个自己喜欢的职业是真正的好职业。但对于多数普通人，经济回报也是职业选择的重要考虑因素。一个有高经济回报的职业一定是市场需求远远大于市场供给的职业，且市场需求要保持长期的增长，而市场供给难以中短期得到补充。

1.4.1 人工智能岗位的市场需求旺盛

根据各大咨询公司的行业研究报告，人工智能相关产业在未来十年预计有 30% ~ 40% 的年增长率。一方面，人工智能的应用会从互联网行业逐渐扩展到金融、工业、农业、能源、城市、交通、医疗、教育等更广泛的行业，应用空间和潜力巨大；另一方面，受限于工智能技术本身的成熟度以及人工智能落地要结合场景的数据处理、系统改造和业务流程优化等条件的制约，人工智能应用的价值释放过程会相对缓慢。这使得市场对人工智能的岗位需求形成了一条稳步又长期增长的曲线，与互联网行业相比，对多数的求职者更加友好，如下图所示。

互联网行业由于技术成熟周期短，应用落地的推进速度快，反而形成一条增长率更高（年增长率超过 100%）但增长周期更短的曲线（电脑互联网时代 10 年，移动互联网时代 10 年）。当行业增长达到顶峰，对岗位的需求也会相应回落，如同 2021 年底的互联网行业的现状。

1.4.2 复合型人才成为市场刚需

在人工智能落地到千行万业的过程中，企业需求量最大、也最为迫切的是既懂行业知识和场景，又懂人工智能理论，还具备实践能力和经验的“复合型人才”。成为“复合型人才”不仅需要学习书本知识，还要大量进行产业实践，使得这种人才有成长深度，供给增长缓慢。从上述分析可见，当人工智能产业在未来几十年保持稳定的增长，而产业需要的“复合型人才”又难以大量供给的情况下，人工智能应用研发岗位会维持一个很好的经济回报。

2. 使用 Python 和 NumPy 构建神经网络模型

上一章我们初步认识了神经网络的基本概念（如神经元、多层连接、前向计算、计算图）和模型结构三要素（模型假设、评价函数和优化算法）。本章将以“波士顿房价预测”任务为例，介绍使用 Python 和 NumPy 来构建神经网络模型的思考过程和操作方法。

波士顿房价预测是一个经典的机器学习任务，类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同，波士顿地区的房价受诸多因素影响。该数据集统计了 13 种可能影响房价的因素和该类型房屋的均价，期望构建一个基于 13 个因素进行房价预测的模型，如下图所示。

对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为①回归任务和②分类任务。因为房价是一个连续值，所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题，并用神经网络来实现这个模型。

2.1 线性回归（Linear Regression）模型

假设房价和各影响因素之间能够用线性关系来描述：

$$y=\sum _{j=1}^M{x}_j{w}_j+b\text{\hspace{1em}(1)}$$

模型的求解即是通过数据拟合出每个 $w_j$ 和 $b$。其中，$w_j$ 和 $b$ 分别表示该线性模型的权重（Weight）和偏置（Bias）。一维情况下，$w_j$ 和 $b$ 是直线的斜率和截距。

线性回归模型使用均方误差（Mean Squared Error，MSE）作为损失函数（Loss），用以衡量预测房价和真实房价的差异，公式如下：

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n({\hat{Y}}_i-Y_i{)}^2\text{\hspace{1em}(2)}$$

思考：

为什么要以均方误差（MSE）作为损失函数？即将模型在每个训练样本上的预测误差加和，来衡量整体样本的准确性。这是因为损失函数的设计不仅仅要考虑“合理性”，同样需要考虑“易解性”，这个问题在后面的内容中会详细阐述。

---

神经网络的标准结构中每个神经元（Neuron）由加权和与非线性变换构成，然后将多个神经元分层的摆放并连接形成神经网络（NN）。线性回归模型可以认为是神经网络模型的一种极简特例，是一个只有加权和、没有非线性变换的神经元（无需形成网络），如下图所示。

2.2 使用 Python 和 NumPy 实现波士顿房价预测任务

深度学习不仅实现了模型的端到端学习，还推动了人工智能进入工业大生产阶段，产生了标准化、自动化和模块化的通用框架。不同场景的深度学习模型具备一定的通用性，五个步骤即可完成模型的构建和训练，如下图所示。

正是由于深度学习的建模和训练的过程存在通用性，在构建不同的模型时，只有模型三要素不同，其它步骤基本一致，深度学习框架才有用武之地。

2.2.1 数据处理

数据处理包含五个部分：①数据导入、②数据形状变换、③数据集划分、④数据归一化处理和⑤封装 load_data 函数。数据一般只有经过预处理后，才能被模型调用。

2.2.1.1 读入数据

通过如下代码读入数据，了解下波士顿房价的数据集结构，数据存放在本地目录下 housing.data 文件中。

数据集下载地址：http://paddlemodels.bj.bcebos.com/uci_housing/housing.data

import numpy as np
import json


# 读取数据
datafile = "/data/data_01/lijiandong/Datasets/boston_house_price/housing.data"
data = np.fromfile(datafile, sep=" ")
print(data)  # /data/data_01/lijiandong/Datasets/boston_house_price/housing.data
print(data.shape)  # (7084,)

2.2.1.2 数据形状变换

由于读入的原始数据是 1 维的，所有数据都连在一起。因此需要我们将数据的形状进行变换，形成一个 2 维的矩阵，每行为一个数据样本（有 14 个列），每个数据样本包含 13 个 $X$（影响房价的特征）和一个 $Y$（该类型房屋的均价）。

"""
读入之后的数据被转化成1维array，其中array的第0-13项是第一条数据，第14-27项是第二条数据，以此类推.... 
这里对原始数据做reshape，变成N x 14的形式
"""
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])

# 查看数据
x = data[0]  # 取第一行
print(x.shape)  # (14,)
print(x)
"""
[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
 4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]
"""

2.2.1.3 数据集划分

将数据集划分成训练集和测试集，其中训练集用于确定模型的参数，测试集用于评判模型的效果。为什么要对数据集进行拆分，而不能直接应用于模型训练呢？这与学生时代的授课和考试关系比较类似，如下图所示。

上学时总有一些自作聪明的同学，平时不认真学习，考试前临阵抱佛脚，将习题死记硬背下来，但是成绩往往并不好。因为学校期望学生掌握的是知识，而不仅仅是习题本身。另出新的考题，才能鼓励学生努力去掌握习题背后的原理。同样我们期望模型学习的是任务的本质规律，而不是训练数据本身，模型训练未使用的数据，才能更真实的评估模型的效果。

在本案例中，我们将 80% 的数据用作训练集，20% 用作测试集，实现代码如下。

ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
test_data = data[offset:]

print(data.shape)  # (506, 14)
print(training_data.shape)  # (404, 14)
print(test_data.shape)  # (102, 14)

通过打印训练集的形状，可以发现共有 404 个样本，每个样本含有 13 个特征和 1 个预测值。

2.2.1.4 数据归一化处理

数据归一化是一种常见的数据预处理技术，用于将数据缩放到一定的范围，通常是 $[0,1]$ 或者 $[-1,1]$ 之间（前者的使用更加广泛，因此我们使用前者）。数据归一化的公式如下：

对于每个特征（或每个列），假设原始数据的范围是 $[\min ,\max ]$，归一化后的数据可以通过以下公式计算：

$$归一化后的数值=\frac{原始数值-\min }{\max -\min }$$

其中，"原始数值"是指特定特征中的原始数据值，"min"是该特征在数据集中的最小值，"max"是该特征在数据集中的最大值。

使用归一化使得每个特征的取值缩放到 $[0,1]$ 之间。这样做有两个好处：

1. 模型训练更高效，在本节的后半部分会详细说明；
2. 特征前的权重大小可以代表该变量对预测结果的贡献度（因为每个特征值本身的范围相同）。

# 计算train数据集的最大值和最小值
maxinums, minimus = training_data.max(axis=0), training_data.min(axis=0)

# 对数据进行归一化处理
for col_name in range(feature_num):
    # 训练集归一化
    training_data[:, col_name] = (training_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
    # 测试集归一化（确保了测试集上的数据也使用了与训练集相同的归一化转换，避免了引入测试集信息污染）
    test_data[:, col_name] = (test_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])

# 验证是否有大于1的值
print(np.any(training_data[:, :-1] > 1.0))  # False
print(np.any(test_data[:, :-1] > 1.0))  # True（这是正常的，因为我们使用了训练集的归一化参数）

2.2.1.5 封装成 load_data 函数

将上述几个数据处理操作封装成 load_data 函数，以便下一步模型的调用，实现方法如下。

import numpy as np
import json


def data_load():
    # 2.2.1.1 读入数据
    datafile = "/data/data_01/lijiandong/Datasets/boston_house_price/housing.data"
    data = np.fromfile(datafile, sep=" ")


    # 2.2.1.2 数据形状变换
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)
    data = data.reshape([data.shape[0] // feature_num, feature_num])  # [N, 14]


    # 2.2.1.3 数据集划分
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    test_data = data[offset:]


    # 2.2.1.4 数据归一化处理
    # 计算train数据集的最大值和最小值
    maxinums, minimus = training_data.max(axis=0), training_data.min(axis=0)

    # 对数据进行归一化处理
    for col_name in range(feature_num):
        # 训练集归一化
        training_data[:, col_name] = (training_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        # 测试集归一化（确保了测试集上的数据也使用了与训练集相同的归一化转换，避免了引入测试集信息污染）
        test_data[:, col_name] = (test_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        
    return training_data, test_data


# 获取数据
training_data, test_data = data_load()
x = training_data[:, :-1]  # 训练数据
target = training_data[:, -1:]  # 目标值

# 查看数据
print(f"x.shape: {
      
      x.shape}")  # (404, 13)
print(f"target.shape: {
      
      target.shape}")  # (404,)

2.2.2 模型设计

模型设计是深度学习模型关键要素之一，也称为网络结构设计，相当于模型的假设空间，即实现模型“前向计算”（从输入到输出）的过程。

如果将输入特征和输出预测值均以向量表示，输入特征 $x$ 有 13 个分量，$y$ 有 1 个分量，那么参数权重的形状（shape）是 $13\times 1$。假设我们以如下任意数字赋值参数做初始化：

$$w=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,-0.1,-0.2,-0.3,-0.4,0.0]$$

用代码表示即：

w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
w = np.array(w).reshape([13, 1])

取出第 1 条样本数据，观察样本的特征向量与参数向量相乘的结果。

x1 = x[0]
t = np.dot(x1, w)
print(t)  # [0.69474855]

完整的线性回归公式，还需要初始化偏移量 $b$，同样随意赋初值 -0.2。那么，线性回归模型的完整输出是 $z=t+b$，这个从特征和参数计算输出值的过程称为“前向计算”。

b = -0.2  # bias
z = t + b
print(z)  # [0.49474855]

将上述计算预测输出的过程以“类和对象”的方式来描述，类成员变量有参数 $w$ 和 $b$。通过写一个 forward 函数（代表“前向计算”）完成上述从特征和参数到输出预测值的计算过程，代码如下所示。

class Network:
    def __init__(self, num_of_weights):
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)  # 随机产生w的初始值
        self.b = 0.0  # 不使用偏置
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z

基于 Network 类的定义，模型的计算过程如下所示。

net = Network(13)
x1 = x[0]
y1 = target[0]
z = net.forward(x1)
print(z)  # [2.39362982]

从上述前向计算的过程可见，线性回归也可以表示成一种简单的神经网络（只有一个神经元，且激活函数为恒等式 $y=y$）。这也是机器学习模型普遍为深度学习模型替代的原因：由于深度学习网络强大的表示能力，很多传统机器学习模型的学习能力等同于相对简单的深度学习模型。

2.2.3 训练配置

模型设计完成后，需要通过训练配置寻找模型的最优值，即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。

通过模型计算 $x_1$ 表示的影响因素所对应的房价应该是 $z$, 但实际数据告诉我们房价是 $y$。这时我们需要有某种指标来衡量预测值 $z$ 跟真实值 $y$ 之间的差距。对于回归问题，最常采用的衡量方法是使用均方误差（MSE）作为评价模型好坏的指标，具体定义如下：

$$\mathrm{Loss}=(y-z{)}^2\text{\hspace{1em}(3)}$$

上式中的 Loss（简记为: $L$）通常也被称作损失函数，它是衡量模型好坏的指标。这里我们需要思考一个问题：如果要衡量预测房价和真实房价之间的差距，是否将每一个样本的差距的绝对值加和即可？差距绝对值加和是更加直观和朴素的思路，为何要平方加和？

这是因为损失函数的设计不仅要考虑准确衡量问题的“合理性”，通常还要考虑“易于优化求解”。至于这个问题的答案，在介绍完优化算法后再揭示。

在回归问题中，均方误差（MSE）是一种比较常见的形式，分类问题中通常会采用交叉熵（Cross Entropy）作为损失函数，在后续的章节中会更详细的介绍。对一个样本计算损失函数值的实现如下。

loss = (y1 - z) ** 2
print(loss)  # [3.88644793]

因为计算损失函数时需要把每个样本的损失函数值都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数 $N$。

$$L=\frac{1}{N}\sum _{i=1}^N(y_i-z_i{)}^2\text{\hspace{1em}(4)}$$

在 Network 类下面添加损失函数的计算过程如下。

class Network:
    def __init__(self, num_of_weights):
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)  # 随机产生w的初始值
        self.b = 0.0  # 不使用偏置
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, pred, gt):
        loss_value_sum = (pred - gt) ** 2
        return np.mean(loss_value_sum)

使用定义的 Network 类，可以方便的计算预测值和损失函数。需要注意的是，类中的变量 x, w, b, pred, gt, loss_value_sum 等均是向量。以变量 x 为例，共有两个维度，一个代表特征数量（值为 13），一个代表样本数量，代码如下所示。

# 组成向量一次性计算多个值
x1 = x[:3]  # 前三行
y1 = target[:3]  # 前三行

pred = net.forward(x1)
print(f"pred: {
      
      pred}")

loss = net.loss(pred, target)
print(f"loss: {
      
      loss}")

结果：

pred: [[2.39362982]
 [2.46752393]
 [2.02483479]]
loss: 3.573658599044957

2.2.4 训练过程

上述计算过程描述了如何构建神经网络，通过神经网络完成预测值和损失函数的计算。接下来介绍如何求解参数 $w$ 和 $b$ 的数值，这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一，其目标是让定义的损失函数 $\mathrm{Loss}$ 尽可能的小，也就是说找到一个参数解 $w$ 和 $b$，使得损失函数取得极小值。

我们先做一个小测试：如下图所示，基于微积分知识，求一条曲线在某个点的斜率等于函数在该点的导数值。那么大家思考下，当处于曲线的极值点时，该点的斜率是多少？

这个问题并不难回答，处于曲线极值点时的斜率为 0，即函数在极值点的导数为 0。那么，让损失函数取极小值的 $w$ 和 $b$ 应该是下述方程组的解：

$$\frac{\partial L}{\partial w}=0\text{\hspace{1em}(5)}$$

$$\frac{\partial L}{\partial b}=0\text{\hspace{1em}(6)}$$

其中 $L$ 表示的是损失函数的值，$w$ 为模型权重，$b$ 为偏置项。$w$ 和 $b$ 均为要学习的模型参数。

把损失函数表示成矩阵的形式，如下：

$$L=\frac{1}{N}||y-(Xw+b)|{|}^2\text{\hspace{1em}(7)}$$

其中 $y$ 为 $N$ 个样本的标签值构成的向量，形状为 $N\times 1$；$X$ 为 $N$ 个样本特征向量构成的矩阵，形状为 $N\times D$，$D$ 为数据特征长度；$w$ 为权重向量，形状为 $D\times 1$；$b$ 为所有元素都为 $b$ 的向量，形状为 $N\times 1$。

计算公式 7 对参数 $b$ 的偏导数：

$$\frac{\partial L}{\partial b}=1^T[y-(Xw+b)]\text{\hspace{1em}(8)}$$

请注意，上述公式忽略了系数 $\frac{2}{N}$，并不影响最后结果。其中 $1$ 为 $N$ 维的全 1 向量。

令公式 8 等于 0，得到

$$b^{\ast }={\overline{x}}^{T}w-\overline{y}\text{\hspace{1em}(9)}$$

其中 $\overline{y}=\frac{1}{N}{1}^{T}y$ 为所有标签的平均值， $\overline{x}=\frac{1}{N}(1^{T}X{)}^T$ 为所有特征向量的平均值。将 $b^{\ast }$ 带入公式 7 中并对参数 $w$ 求偏导得到

$$\frac{\partial L}{\partial w}=(X-{\overline{x}}^T{)}^T[(y-\overline{y})-(X-{\overline{x}}^T)w]\text{\hspace{1em}(10)}$$

令公式 10 等于 0，得到最优参数

$$w^{\ast }=[(X-{\overline{x}}^T{)}^T(X-{\overline{x}}^T){]}^{-1}(X-{\overline{x}}^T{)}^T(y-\overline{y})\text{\hspace{1em}(11)}$$

$$b^{\ast }={\overline{x}}^T{w}^{\ast }-\overline{y}\text{\hspace{1em}(12)}$$

将样本数据 $(x,y)$ 带入上面的公式 11 和公式 12 中即可求解出 $w$ 和 $b$ 的值，但这种方法只对线性回归这样简单的任务有效。如果模型中含有非线性变换，或者损失函数不是均方差这种简单的形式，则很难通过上式求解。为了解决这个问题，下面我们将引入更加普适的数值求解方法：梯度下降法。

2.2.4.1 梯度下降法

在现实中存在大量的函数正向求解容易，但反向求解较难，被称为单向函数，这种函数在密码学中有大量的应用。密码锁的特点是可以迅速判断一个密钥是否是正确的(已知 $x$，求 $y$ 很容易)，但是即使获取到密码锁系统，也无法破解出正确得密钥（已知 $y$，求 $x$ 很难）。

这种情况特别类似于一位想从山峰走到坡谷的盲人，他看不见坡谷在哪（无法逆向求解出 $\mathrm{Loss}$ 导数为 0 时的参数值），但可以伸脚探索身边的坡度（当前点的导数值，也称为梯度）。那么，求解 Loss 函数最小值可以这样实现：从当前的参数取值，一步步的按照下坡的方向下降，直到走到最低点。这种方法笔者称它为“盲人下坡法”。哦不，有个更正式的说法“梯度下降法”。

训练的关键是找到一组 $(w,b)$，使得损失函数 $L$ 取极小值。我们先看一下损失函数 $L$ 只随两个参数 $w_5$ 和 $w_9$ 变化时的简单情形，启发下寻解的思路。

$$L=L(w_5,w_9)\text{\hspace{1em}(13)}$$

这里将 $w_0,w_1,...,w_{12}$ 中除 $w_5,w_9$ 之外的参数和 $b$ 都固定下来，可以用图画出 $L(w_5,w_9)$ 的形式，并在三维空间中画出损失函数随参数变化的曲面图。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


net = Network(num_of_weights=13)

# 只画出参数w5和w9在区间[-160, 160]的曲线部分，以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros(shape=[len(w5), len(w9)])

# 计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
    for j in range(len(w9)):
        # 更改模型参数的数值
        net.w[5] = w5[i]
        net.w[9] = w9[i]
        
        # 模型infer并计算、记录loss
        pred = net.forward(x)
        loss = net.loss(pred=pred, gt=target)
        losses[i, j] = loss
        
# 使用matplotlib将两个变量和对应的Loss作3D图
fig = plt.figure(dpi=300)
ax = fig.add_axes(Axes3D(fig))

# 设置坐标轴标签
ax.set_xlabel('w5')
ax.set_ylabel('w9')
ax.set_zlabel('Loss')

w5, w9 = np.meshgrid(w5, w9)

ax.plot_surface(w5, w9, losses, rstride=1,cstride=1, cmap="rainbow")
plt.savefig("gd_sample_demo.png")

从图中可以明显观察到有些区域的函数值比周围的点小。需要说明的是：为什么选择 $w_5$ 和 $w_9$ 来画图呢？这是因为选择这两个参数的时候，可比较直观的从损失函数的曲面图上发现极值点的存在。其他参数组合，从图形上观测损失函数的极值点不够直观。

观察上述曲线呈现出“圆滑”的坡度，这正是我们选择以均方误差作为损失函数的原因之一。下图呈现了只有一个参数维度时，均方误差和绝对值误差（只将每个样本的误差累加，不做平方处理）的损失函数曲线图。

由此可见，均方误差表现的“圆滑”的坡度有两个好处：

1. 曲线的最低点是可导的。
2. 越接近最低点，曲线的坡度逐渐放缓，有助于通过当前的梯度来判断接近最低点的程度（是否逐渐减少步长，以免错过最低点）。

绝对值误差是不具备这两个特性的，这也是损失函数的设计不仅仅要考虑“合理性”，还要追求“易解性”的原因。

现在我们要找出一组 $[w_5,w_9]$ 的值，使得损失函数最小，实现梯度下降法的方案如下：

• 步骤 1：随机的选一组初始值，例如：$[w_5,w_9]=[-100.0,-100.0]$
• 步骤 2：选取下一个点 $[w_5^{\prime },w_9^{\prime }]$ ，使得 $L(w_5^{\prime },w_9^{\prime })<L(w_5,w_9)$
• 步骤 3：重复步骤 2，直到损失函数几乎不再下降。

如何选择 $[w_5^{\prime },w_9^{\prime }]$ 是至关重要的，第一要保证 $L$ 是下降的，第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们：沿着梯度的反方向，是函数值下降最快的方向，如下图所示。简单理解，函数在某一个点的梯度方向是曲线斜率最大的方向，但梯度方向是向上的，所以下降最快的是梯度的反方向。

2.2.4.2 梯度计算

上文已经介绍了损失函数的计算方法，这里稍微改写。为了使梯度计算更加简洁，引入因子 $\frac{1}{2}$，定义损失函数如下：

$$L=\frac{1}{2N}\sum _{i=1}^N(y_i-z_i{)}^2\text{\hspace{1em}(14)}$$

其中 $z_i$ 是网络对第 $i$ 个样本的预测值：

$$z_i=\sum _{j=0}^{12}{x}_i^j\cdot w_j+b\text{\hspace{1em}(15)}$$

梯度的定义：

$$\mathrm{gradient}=(\frac{\partial L}{\partial w_0},\frac{\partial L}{\partial w_1},...,\frac{\partial L}{\partial w_{12}},\frac{\partial L}{\partial b})\text{\hspace{1em}(16)}$$

可以计算出 $L$ 对 $w$ 和 $b$ 的偏导数：

$$\begin{array}{rl}\frac{\partial L}{\partial w_j}& =\frac{1}{N}\sum _{i=1}^N(z_i-y_i)\frac{\partial z_i}{\partial w_j}\\ & =\frac{1}{N}\sum _{i=1}^N(z_i-y_i)x_i^j\end{array}\text{\hspace{1em}(17)}$$

$$\begin{array}{rl}\frac{\partial L}{\partial b}& =\frac{1}{N}\sum _{i=1}^N(z_i-y_i)\frac{\partial z_i}{\partial b}\\ & =\frac{1}{N}\sum _{i=1}^N(z_i-y_i)\end{array}\text{\hspace{1em}(18)}$$

从导数的计算过程可以看出，因子 $\frac{1}{2}$ 被消掉了，这是因为二次函数求导的时候会产生因子
2，这也是我们将损失函数改写的原因。

下面我们考虑只有一个样本的情况下，计算梯度：

$$L=\frac{1}{2}(y_i-z_i{)}^2\text{\hspace{1em}(19)}$$

$$z_1=x_1^0\cdot w_0+x_1^1\cdot w_1+...+x_1^{12}\cdot w_{12}+b\text{\hspace{1em}(20)}$$

可以计算出：

$$L=\frac{1}{2}(x_1^0\cdot w_0+x_1^1\cdot w_1+...+x_1^{12}\cdot w_{12}+b-y_1{)}^2\text{\hspace{1em}(21)}$$

可以计算出 $L$ 对 $w$ 和 $b$ 的偏导数：

$$\begin{array}{rl}\frac{\partial L}{\partial w_0}& =(x_1^0\cdot w_0+x_1^1\cdot w_1+...+x_1^{12}\cdot w_{12}+b-y_1)\cdot x_1^0\\ & =(z_1-y_1)\cdot x_1^0\end{array}\text{\hspace{1em}(22)}$$

$$\begin{array}{rl}\frac{\partial L}{\partial b}& =(x_1^0\cdot w_0+x_1^1\cdot w_1+...+x_1^{12}\cdot w_{12}+b-y_1)\cdot 1\\ & =(z_1-y_1)\end{array}\text{\hspace{1em}(23)}$$

可以通过具体的程序查看每个变量的数据和维度。

x1 = x[0]
y1 = target[0]
z1 = net.forward(x1)
print(f"x1.shape: {
      
      x1.shape}, The value is: {
      
      x1}")
print(f"y1.shape: {
      
      y1.shape}, The value is: {
      
      y1}")
print(f"z1.shape: {
      
      z1.shape}, The value is: {
      
      z1}")

结果：

x1.shape: (13,), The value is: 
[0.         0.18       0.07344184 0.         0.31481481 0.57750527
 0.64160659 0.26920314 0.         0.22755741 0.28723404 1.
 0.08967991]
y1.shape: (1,), The value is: [0.42222222]
z1.shape: (1,), The value is: [130.86954441]

按上面的公式，当只有一个样本时，可以计算某个 $w_j$，比如 $w_0$ 的梯度。

gradient_w0 = (z1 - y1) * x1[0]
print(f"The gradient of w0 is: {
      
      gradient_w0}")  # [0.]

同样我们可以计算 $w_1$ 的梯度。

gradient_w1 = (z1 - y1) * x1[1]
print(f"The gradient of w1 is: {
      
      gradient_w1}")  # [0.35485337]

依次计算 $w_j$ 的梯度。

gradients_of_weights = []
for i in range(net.w.shape[0]):
    gradient = (z1 - y1) * x1[i]
    gradients_of_weights.append(gradient)
    
print(gradients_of_weights)

结果：

[array([0.]), array([0.35485337]), array([0.14478381]), array([0.]), array([0.62062832]), array([1.13849828]), array([1.26486811]), array([0.53070911]), array([0.]), array([0.44860841]), array([0.56625537]), array([1.9714076]), array([0.17679566])]

2.2.4.3 使用 NumPy 进行梯度计算

基于 NumPy 广播机制（对向量和矩阵计算如同对 1 个单一变量计算一样），可以更快速的实现梯度计算。计算梯度的代码中直接用 $(z_1-y_1)\cdot x_1$，得到的是一个 13 维的向量，每个分量分别代表该维度的梯度。

gradient_w = (z1 - y1) * x1
print(f"[The gradient of w by sampled] gradient_w.shape: {
      
      gradient_w.shape}, gradient_w: \r\n{
      
      gradient_w}")

结果：

[The gradient of w by sampled] gradient_w.shape: (13,), gradient_w: 
[0.         0.35485337 0.14478381 0.         0.62062832 1.13849828
 1.26486811 0.53070911 0.         0.44860841 0.56625537 1.9714076
 0.17679566]

输入数据中有多个样本，每个样本都对梯度有贡献。如上代码计算了只有样本 1 时的梯度值，同样的计算方法也可以计算样本 2 和样本 3 对梯度的贡献。

for i in range(x.shape[0]):
    input = x[i]
    gt = target[i]
    pred = net.forward(input)
    gradient = (pred - gt) * input
    if 1 <= i <= 3:
        print(f"[The gradient of w by sampled_{
      
      i}] gradient.shape: {
      
      gradient.shape}, gradient: \r\n{
      
      gradient}")

结果：

[The gradient of w by sampled_1] gradient.shape: (13,), gradient: 
[4.95115308e-04 0.00000000e+00 5.50693832e-01 0.00000000e+00
 3.62727044e-01 1.15004718e+00 1.64259797e+00 7.32343840e-01
 9.12450018e-02 2.40970621e-01 1.16094704e+00 2.09863504e+00
 4.29108324e-01]
 
[The gradient of w by sampled_2] gradient.shape: (13,), gradient: 
[3.21688482e-04 0.00000000e+00 3.58140452e-01 0.00000000e+00
 2.35897372e-01 9.47722033e-01 8.18057517e-01 4.76275452e-01
 5.93406432e-02 1.56713807e-01 7.55014992e-01 1.34780052e+00
 8.66203097e-02]
 
[The gradient of w by sampled_3] gradient.shape: (13,), gradient: 
[2.95458209e-04 0.00000000e+00 6.89019665e-02 0.00000000e+00
 1.51571633e-01 6.64543743e-01 4.45830114e-01 4.52623356e-01
 8.77472466e-02 7.37333335e-02 6.54837165e-01 1.00206898e+00
 3.36921340e-02]

可能有的读者再次想到可以使用 for 循环把每个样本对梯度的贡献都计算出来，然后再作平均。但是我们不需要这么做，仍然可以使用 NumPy 的矩阵操作来简化运算，如 3 个样本的情况。

# 注意这里是一次取出3个样本的数据，不是取出第3个样本
x_3_samples = x[:3]
y_3_samples = target[:3]
z_3_samples = net.forward(x_3_samples)

print('x {}, shape {}'.format(x_3_samples, x_3_samples.shape))
print('y {}, shape {}'.format(y_3_samples, y_3_samples.shape))
print('z {}, shape {}'.format(z_3_samples, z_3_samples.shape))

x [[0.00000000e+00 1.80000000e-01 7.34418420e-02 0.00000000e+00
  3.14814815e-01 5.77505269e-01 6.41606591e-01 2.69203139e-01
  0.00000000e+00 2.27557411e-01 2.87234043e-01 1.00000000e+00
  8.96799117e-02]
 [2.35922539e-04 0.00000000e+00 2.62405717e-01 0.00000000e+00
  1.72839506e-01 5.47997701e-01 7.82698249e-01 3.48961980e-01
  4.34782609e-02 1.14822547e-01 5.53191489e-01 1.00000000e+00
  2.04470199e-01]
 [2.35697744e-04 0.00000000e+00 2.62405717e-01 0.00000000e+00
  1.72839506e-01 6.94385898e-01 5.99382080e-01 3.48961980e-01
  4.34782609e-02 1.14822547e-01 5.53191489e-01 9.87519166e-01
  6.34657837e-02]], shape (3, 13)
  
y [[0.42222222]
 [0.36888889]
 [0.66      ]], shape (3, 1)
 
z [[2.39362982]
 [2.46752393]
 [2.02483479]], shape (3, 1)

x_3_samples, y_3_samples , z_3_samples 的第一维大小均为 3，表示有 3 个样本,下面计算这 3 个样本对梯度的贡献。

gradient_w = (z_3_samples - y_3_samples) * x_3_samples
print('gradient_w {}, gradient.shape {}'.format(gradient_w, gradient_w.shape))

gradient_w [[0.00000000e+00 3.54853368e-01 1.44783806e-01 0.00000000e+00
  6.20628319e-01 1.13849828e+00 1.26486811e+00 5.30709115e-01
  0.00000000e+00 4.48608410e-01 5.66255375e-01 1.97140760e+00
  1.76795660e-01]
 [4.95115308e-04 0.00000000e+00 5.50693832e-01 0.00000000e+00
  3.62727044e-01 1.15004718e+00 1.64259797e+00 7.32343840e-01
  9.12450018e-02 2.40970621e-01 1.16094704e+00 2.09863504e+00
  4.29108324e-01]
 [3.21688482e-04 0.00000000e+00 3.58140452e-01 0.00000000e+00
  2.35897372e-01 9.47722033e-01 8.18057517e-01 4.76275452e-01
  5.93406432e-02 1.56713807e-01 7.55014992e-01 1.34780052e+00
  8.66203097e-02]], gradient.shape (3, 13)

此处可见，计算梯度 gradient_w 的维度是 $3\times 13$，并且其第 1 行与上面第 1 个样本计算的梯度 gradient_w_by_sample1一致，第 2 行与上面第 2 个样本计算的梯度 gradient_w_by_sample2 一致，第 3 行与上面第 3 个样本计算的梯度 gradient_w_by_sample3 一致。这里使用矩阵操作，可以更加方便的对 3 个样本分别计算各自对梯度的贡献。

那么对于有 $N$ 个样本的情形，我们可以直接使用如下方式计算出所有样本对梯度的贡献，这就是使用 NumPy 库广播功能带来的便捷。 小结一下这里使用 NumPy 库的广播功能：

• 一方面可以扩展参数的维度，代替 for 循环来计算 1 个样本对从 $w_0$ 到 $w_{12}$ 的所有参数的梯度。
• 另一方面可以扩展样本的维度，代替 for 循环来计算样本 0 到样本 403 对参数的梯度。

z = net.forward(x)
gradient_w = (z - target) * x
print('gradient_w shape {}'.format(gradient_w.shape))
print(gradient_w)

gradient_w shape (404, 13)
[[0.00000000e+00 3.54853368e-01 1.44783806e-01 ... 5.66255375e-01
  1.97140760e+00 1.76795660e-01]
 [4.95115308e-04 0.00000000e+00 5.50693832e-01 ... 1.16094704e+00
  2.09863504e+00 4.29108324e-01]
 [3.21688482e-04 0.00000000e+00 3.58140452e-01 ... 7.55014992e-01
  1.34780052e+00 8.66203097e-02]
 ...
 [7.66711387e-01 0.00000000e+00 3.35694398e+00 ... 3.87578270e+00
  4.79373123e+00 2.45903597e+00]
 [4.83683601e-01 0.00000000e+00 3.14256160e+00 ... 3.62826605e+00
  4.20149273e+00 2.30075782e+00]
 [1.42480820e+00 0.00000000e+00 3.58013213e+00 ... 4.13346610e+00
  5.11244491e+00 2.54493671e+00]]

上面 gradient_w 的每一行代表了一个样本对梯度的贡献。根据梯度的计算公式，总梯度是对每个样本对梯度贡献的平均值。

$$\begin{array}{rl}\frac{\partial L}{\partial w_j}& =\frac{1}{N}\sum _{i=1}^N(z_i-y_i)\frac{\partial z_i}{\partial w_j}\\ & =\frac{1}{N}\sum _{i=1}^N(z_i-y_i)x_i^j\end{array}\text{\hspace{1em}(17)}$$

可以使用 NumPy 的均值函数来完成此过程，代码实现如下。

# axis = 0 表示把每一行做相加然后再除以总的行数
gradient_w = np.mean(gradient_w, axis=0)
print('gradient_w ', gradient_w.shape)
print('w ', net.w.shape)
print(gradient_w)
print(net.w)

gradient_w  (13,)
w  (13, 1)
[0.10197566 0.20327718 1.21762392 0.43059902 1.05326594 1.29064465
 1.95461901 0.5342187  0.88702053 1.15069786 1.5790441  2.43714929
 0.87116361]
[[ 1.76405235]
 [ 0.40015721]
 [ 0.97873798]
 [ 2.2408932 ]
 [ 1.86755799]
 [-0.97727788]
 [ 0.95008842]
 [-0.15135721]
 [-0.10321885]
 [ 0.4105985 ]
 [ 0.14404357]
 [ 1.45427351]
 [ 0.76103773]]

使用 NumPy 的矩阵操作方便地完成了 gradient 的计算，但引入了一个问题，gradient_w 的形状是 $(13,)$，而 $w$ 的维度是 $(13,1)$。导致该问题的原因是使用 np.mean函数时消除了第 0 维。为了加减乘除等计算方便，gradient_w 和 $w$ 必须保持一致的形状。因此我们将 gradient_w 的维度也设置为 $(13,1)$，代码如下：

gradient_w = gradient_w[:, np.newaxis]
print('gradient_w shape', gradient_w.shape)  # gradient_w shape (13, 1)

综合上面的剖析，计算梯度的代码如下所示。

pred = net.forward(x)
gradient_w = (pred - target) * x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
print(gradient_w)

[[0.10197566]
 [0.20327718]
 [1.21762392]
 [0.43059902]
 [1.05326594]
 [1.29064465]
 [1.95461901]
 [0.5342187 ]
 [0.88702053]
 [1.15069786]
 [1.5790441 ]
 [2.43714929]
 [0.87116361]]

上述代码非常简洁地完成了 $w$ 的梯度计算。同样，计算 $b$ 的梯度的代码也是类似的原理。

gradient_b = (pred - target)
gradient_b = np.mean(gradient_b)
# 此处b是一个数值，所以可以直接用np.mean得到一个标量
print(gradient_b)  # 2.599327274554706

将上面计算 $w$ 和 $b$ 的梯度的过程，写成 Network 类的 gradient 函数，实现方法如下所示。

class Network_with_gradient:
    def __init__(self, num_of_weights):
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)  # 随机产生w的初始值
        self.b = 0.0  # 不使用偏置
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, pred, gt):
        loss_value_sum = (pred - gt) ** 2
        return np.mean(loss_value_sum)
    
    def gradient(self, x, gt):
        pred = self.forward(x)
        gradient_w = (pred - gt) * x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (pred - gt)
        gradient_b = np.mean(gradient_b)
        
        return gradient_w, gradient_b
    
    
# 初始化网络
net = Network_with_gradient(13)
# 设置[w5, w9] = [-100., -100.]
net.w[5] = -100.0
net.w[9] = -100.0

pred = net.forward(x)
loss = net.loss(pred, target)
gradient_w, gradient_b = net.gradient(x, target)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))

point [-100.0, -100.0], loss 7873.345739941161
gradient [-45.87968288123223, -35.50236884482904]

2.2.4.4 梯度更新

下面研究更新梯度的方法，确定损失函数更小的点。首先沿着梯度的反方向移动一小步，找到下一个点 $P_1$，观察损失函数的变化。

# 在[w5, w9]平面上，沿着梯度的反方向移动到下一个点P1
# 定义移动步长 eta
eta = 0.1
# 更新参数w5和w9
net.w[5] = net.w[5] - eta * gradient_w5
net.w[9] = net.w[9] - eta * gradient_w9
# 重新计算z和loss
pred = net.forward(x)
loss = net.loss(pred, target)
gradient_w, gradient_b = net.gradient(x, target)
gradient_w5 = gradient_w[5][0]
gradient_w9 = gradient_w[9][0]
print('point {}, loss {}'.format([net.w[5][0], net.w[9][0]], loss))
print('gradient {}'.format([gradient_w5, gradient_w9]))

point [-95.41203171187678, -96.4497631155171], loss 7214.694816482369
gradient [-43.883932999069096, -34.019273908495926]

运行上面的代码，可以发现沿着梯度反方向走一小步，下一个点的损失函数的确减少了。感兴趣的话，大家可以尝试不停的点击上面的代码块，观察损失函数是否一直在变小。

在上述代码中，每次更新参数使用的语句： net.w[5] = net.w[5] - eta * gradient_w5

• 相减：参数需要向梯度的反方向移动。
• eta：控制每次参数值沿着梯度反方向变动的大小，即每次移动的步长，又称为学习率。

大家可以思考下，为什么之前我们要做输入特征的归一化，保持尺度一致？这是为了让统一的步长更加合适，使训练更加高效。

如下图所示，特征输入归一化后，不同参数输出的 Loss 是一个比较规整的曲线，学习率可以设置成统一的值 ；特征输入未归一化时，不同特征对应的参数所需的步长不一致，尺度较大的参数需要大步长，尺寸较小的参数需要小步长，导致无法设置统一的学习率。

2.2.4.5 封装 Train 函数

将上面的循环计算过程封装在 train 和 update 函数中，实现方法如下所示。

import numpy as np
import json
import matplotlib.pyplot as plt


class Network_with_gradient:
    def __init__(self, num_of_weights):
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)  # 随机产生w的初始值
        self.b = 0.0  # 不使用偏置
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, pred, gt):
        loss_value_sum = (pred - gt) ** 2
        return np.mean(loss_value_sum)
    
    def gradient(self, x, gt):
        pred = self.forward(x)
        gradient_w = (pred - gt) * x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (pred - gt)
        gradient_b = np.mean(gradient_b)
        
        return gradient_w, gradient_b
    
    def update(self, gradient_w5, gradient_w9, lr=0.01):
        self.w[5] = self.w[5] - lr * gradient_w5
        self.w[9] = self.w[9] - lr * gradient_w9
        
    def train(self, inp, gt, interations=100, lr=0.01):
        pts = []
        losses = []
        
        for i in range(interations):
            pts.append([self.w[5][0], self.w[9][0]])
            pred = self.forward(inp)
            loss = self.loss(pred, gt)
            gradient_w, gradient_b = self.gradient(x=inp, gt=gt)
            gradient_w5 = gradient_w[5][0]
            gradient_w9 = gradient_w[9][0]
            self.update(gradient_w5, gradient_w9, lr=lr)
            losses.append(loss)
            
            if i % 50 == 0:
                print(f"iter: {
      
      i}, point: {
      
      [self.w[5][0], self.w[9][0]]}, Loss: {
      
      loss}")
        return pts, losses


def data_load():
    # 2.2.1.1 读入数据
    datafile = "/data/data_01/lijiandong/Datasets/boston_house_price/housing.data"
    data = np.fromfile(datafile, sep=" ")


    # 2.2.1.2 数据形状变换
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)
    data = data.reshape([data.shape[0] // feature_num, feature_num])  # [N, 14]


    # 2.2.1.3 数据集划分
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    test_data = data[offset:]


    # 2.2.1.4 数据归一化处理
    # 计算train数据集的最大值和最小值
    maxinums, minimus = training_data.max(axis=0), training_data.min(axis=0)

    # 对数据进行归一化处理
    for col_name in range(feature_num):
        # 训练集归一化
        training_data[:, col_name] = (training_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        # 测试集归一化（确保了测试集上的数据也使用了与训练集相同的归一化转换，避免了引入测试集信息污染）
        test_data[:, col_name] = (test_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        
    return training_data, test_data
    
    
if __name__ == "__main__":
    # 获取数据
    train_data, test_data = data_load()
    inputs = train_data[:, :-1]
    targets = train_data[:, -1:]
    
    # 创建网络
    model = Network_with_gradient(num_of_weights=13)
    num_iteration = 2000
    
    # 启动训练
    points, losses = model.train(inputs, targets, num_iteration, lr=0.01)
    
    # 画出损失函数的变化趋势
    plot_x = np.arange(num_iteration)
    plot_y = np.array(losses)
    plt.plot(plot_x, plot_y)
    plt.xlabel("Iteration")
    plt.ylabel("Loss")
    plt.savefig("test_model_loss.png")

iter: 0, point: [-0.9901843263352099, 0.39909152329488246], Loss: 8.74595446663459
iter: 50, point: [-1.565620876463878, -0.12301073215571104], Loss: 6.306355217447029
iter: 100, point: [-2.022354418155828, -0.5542991021920926], Loss: 4.711795652571785
iter: 150, point: [-2.3835826672990916, -0.9119900464266062], Loss: 3.6675975768722684
...
iter: 1850, point: [-3.2091283870302365, -3.3267726714708044], Loss: 1.4862553256192466
iter: 1900, point: [-3.1961376490600024, -3.344849195951625], Loss: 1.4842710198735334
iter: 1950, point: [-3.183547669731126, -3.3622933329823237], Loss: 1.4824177199043154

2.2.4.6 训练过程扩展到全部参数

为了能给读者直观的感受，上文演示的梯度下降的过程仅包含 $w_5$ 和 $w_9$ 两个参数。但房价预测的模型必须要对所有参数 $w$ 和 $b$ 进行求解，这需要将 Network 中的 update 和 train 函数进行修改。由于不再限定参与计算的参数（所有参数均参与计算），修改之后的代码反而更加简洁。

实现逻辑：

1. 前向计算输出
2. 根据输出和真实值计算 Loss
3. 基于 Loss 和输入计算梯度
4. 根据梯度更新参数值

四个部分反复执行，直到到损失函数最小。

import numpy as np
import json
import matplotlib.pyplot as plt


class Network_full_weights:
    def __init__(self, num_of_weights):
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)  # 随机产生w的初始值
        self.b = 0.0  # 不使用偏置
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, pred, gt):
        loss_value_sum = (pred - gt) ** 2
        return np.mean(loss_value_sum)
    
    def gradient(self, x, gt):
        pred = self.forward(x)
        gradient_w = (pred - gt) * x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (pred - gt)
        gradient_b = np.mean(gradient_b)
        
        return gradient_w, gradient_b
    
    def update(self, gradient_w, gradient_b, lr=0.01):
        self.w = self.w - lr * gradient_w  # 负梯度，所以是减
        self.b = self.b - lr * gradient_b  # 负梯度，所以是减
        
    def train(self, inp, gt, interations=100, lr=0.01):
        pts = []
        losses = []
        
        for i in range(interations):
            pts.append([self.w[5][0], self.w[9][0]])
            pred = self.forward(inp)
            loss = self.loss(pred, gt)
            gradient_w, gradient_b = self.gradient(x=inp, gt=gt)
            self.update(gradient_w, gradient_b, lr=lr)
            losses.append(loss)
            
            if i % 50 == 0:
                print(f"iter: {
      
      i}, point: {
      
      [self.w[5][0], self.w[9][0]]}, Loss: {
      
      loss}")
        return pts, losses


def data_load():
    # 2.2.1.1 读入数据
    datafile = "/data/data_01/lijiandong/Datasets/boston_house_price/housing.data"
    data = np.fromfile(datafile, sep=" ")


    # 2.2.1.2 数据形状变换
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)
    data = data.reshape([data.shape[0] // feature_num, feature_num])  # [N, 14]


    # 2.2.1.3 数据集划分
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    test_data = data[offset:]


    # 2.2.1.4 数据归一化处理
    # 计算train数据集的最大值和最小值
    maxinums, minimus = training_data.max(axis=0), training_data.min(axis=0)

    # 对数据进行归一化处理
    for col_name in range(feature_num):
        # 训练集归一化
        training_data[:, col_name] = (training_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        # 测试集归一化（确保了测试集上的数据也使用了与训练集相同的归一化转换，避免了引入测试集信息污染）
        test_data[:, col_name] = (test_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        
    return training_data, test_data
    
    
if __name__ == "__main__":
    # 获取数据
    train_data, test_data = data_load()
    inputs = train_data[:, :-1]
    targets = train_data[:, -1:]
    
    # 创建网络
    model = Network_full_weights(num_of_weights=13)
    num_iteration = 2000
    
    # 启动训练
    points, losses = model.train(inputs, targets, num_iteration, lr=0.01)
    
    # 画出损失函数的变化趋势
    plot_x = np.arange(num_iteration)
    plot_y = np.array(losses)
    plt.plot(plot_x, plot_y)
    plt.xlabel("Iteration")
    plt.ylabel("Loss")
    plt.savefig("test_model_loss.png")

iter: 0, point: [-0.9901843263352099, 0.39909152329488246], Loss: 8.74595446663459
iter: 50, point: [-1.2510816196755312, 0.10537114344977061], Loss: 1.2774697388163774
iter: 100, point: [-1.248700167154482, 0.013128221346003856], Loss: 0.8996702309578077
iter: 150, point: [-1.207833898147619, -0.03959546161885696], Loss: 0.7517595081577438
iter: 200, point: [-1.1647360167738359, -0.08022928159585666], Loss: 0.639972629138626
...
iter: 1850, point: [-0.593635514684025, -0.23371944218812102], Loss: 0.10208939582379549
iter: 1900, point: [-0.5835935123829064, -0.23148564712851874], Loss: 0.09960847979302702
iter: 1950, point: [-0.5736614290879241, -0.2292815676008641], Loss: 0.09724348540057882

2.2.4.7 随机梯度下降法（ Stochastic Gradient Descent）

在上述程序中，每次损失函数和梯度计算都是基于数据集中的全量数据。对于波士顿房价预测任务数据集而言，样本数比较少，只有 404 个。但在实际问题中，数据集往往非常大，如果每次都使用全量数据进行计算，效率非常低，通俗地说就是“杀鸡焉用牛刀”。由于参数每次只沿着梯度反方向更新一点点，因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数，这种方法被称作随机梯度下降法（Stochastic Gradient Descent，SGD），核心概念如下：

• mini-batch：每次迭代时抽取出来的一批数据被称为一个 mini-batch。
• batch_size：一个 mini-batch 所包含的样本数目称为 batch_size。
• epoch：当程序迭代的时候，按 mini-batch 逐渐抽取出样本，当把整个数据集都遍历到了的时候，则完成了一轮训练，也叫一个 epoch。启动训练时，可以将训练的轮数 num_epochs 和 batch_size 作为参数传入。

下面结合程序介绍具体的实现过程，涉及到数据处理和训练过程两部分代码的修改。

2.2.4.7.1 数据处理代码修改

数据处理需要实现拆分数据批次和样本乱序（为了实现随机抽样的效果）两个功能。

# 获取数据
train_data, test_data = data_load()
print(train_data.shape)  # (404, 14)

train_data 中一共包含 404 条数据，如果 batch_size=10，即取前 0 ~ 9 号样本作为第一个 mini-batch，命名 train_data1。

train_data1 = train_data[:10]
print(train_data1.shape)  # (10, 14)

使用 train_data1 的数据（0 ~ 9 号样本）计算梯度并更新网络参数。

# 获取数据
train_data, test_data = data_load()
print(train_data.shape)  # (404, 14)

train_data1 = train_data[:10]
print(train_data1.shape)  # (10, 14)

model = Network_full_weights(13)
inputs = train_data1[:, :-1]
targets = train_data1[:, -1:]

points, losses = model.train(inputs, targets, 1, lr=0.01)
print(losses[0])  # 4.497480200683046

再取出 10 ~ 19 号样本作为第二个 mini-batch，计算梯度并更新网络参数。按此方法不断的取出新的 mini-batch，并逐渐更新网络参数。

接下来，将 train_data 分成大小为 batch_size 的多个 mini_batch，如下代码所示：将 train_data分成 $\frac{404}{10}+1=41$ 个 mini_batch，其中前 40 个 mini_batch，每个均含有 10 个样本，最后一个 mini_batch 只含有 4 个样本。

# 获取数据
train_data, test_data = data_load()
batch_size = 10
n = len(train_data)
mini_batches = [train_data[k: k+batch_size] for k in range(0, n, batch_size)]  # 如果不够k+batch_size了，那么就取完

print(f"第一个mini_batch的shape为: {
      
      mini_batches[0].shape}")  # (10, 14)
print(f"最后一个mini_batch的shape为: {
      
      mini_batches[-1].shape}")  # (4, 14)

另外，这里是按顺序读取 mini_batch，而 SGD 里面是随机抽取一部分样本代表总体。为了实现随机抽样的效果，我们先将 train_data 里面的样本顺序随机打乱，然后再抽取 mini_batch。随机打乱样本顺序，需要用到 np.random.shuffle 函数，下面先介绍它的用法。

说明：通过大量实验发现，模型受训练后期的影响更大，类似于人脑总是对近期发生的事情记忆的更加清晰。为了避免数据样本集合的顺序干扰模型的训练效果，需要进行样本乱序操作。当然，如果训练样本的顺序就是样本产生的顺序，而我们期望模型更重视近期产生的样本（预测样本会和近期的训练样本分布更接近），则不需要乱序这个步骤。

a = np.array(list(range(1, 13)))
print(f"Shuffle前的数组为: {
      
      a}")  # [ 1  2  3  4  5  6  7  8  9 10 11 12]
np.random.shuffle(a)  # inplace操作
print(f"Shuffle后的数组为: {
      
      a}")  # [ 6  9  1 11  4 10  7  3  2 12  5  8]

多次运行上面的代码，可以发现每次执行 shuffle 函数后的数字顺序均不同。 上面举的是一个 1 维数组乱序的案例，我们再观察下 2 维数组乱序后的效果。

a = np.array(list(range(1, 13))).reshape([6, 2])
print(f"Shuffle前的数组为: \r\n{
      
      a}")
np.random.shuffle(a)  # inplace操作
print(f"Shuffle后的数组为: \r\n{
      
      a}")

Shuffle前的数组为: 
[[ 1  2]
 [ 3  4]
 [ 5  6]
 [ 7  8]
 [ 9 10]
 [11 12]]
 
Shuffle后的数组为: 
[[ 5  6]
 [ 1  2]
 [ 3  4]
 [11 12]
 [ 9 10]
 [ 7  8]]

观察运行结果可发现，数组的元素在第 0 维被随机打乱，但第 1 维的顺序保持不变。例如数字 2 仍然紧挨在数字 1 的后面，数字 8 仍然紧挨在数字 7 的后面，而第二维的 [3, 4] 并不排在 [1, 2] 的后面。将这部分实现 SGD 算法的代码集成到 Network 类中的 train 函数中，最终的完整代码如下。

# 获取数据
train_data, test_data = data_load()
    
# Shuffle
# 在训练集需要进行shuffle（随机打乱样本顺序）的情况下，测试
np.random.shuffle(train_data)
    
# 将 train_data 分成多个 mini_batch
batch_size = 10
n = len(train_data)
mini_batches = [train_data[k: k+batch_size] for k in range(0
    
# 创建网络
model = Network_full_weights(13)
# 依次使用每个mini_batch的数据
for idx, mini_batch in enumerate(mini_batches):
    inputs = mini_batch[:, :-1]
    targets = mini_batch[:, -1:]
    loss = model.train(inputs, targets, interations=1, lr=0.
    print(f"mini_batch[{
      
      idx}]'s loss: {
      
      loss}")

iter: 0, point: [-0.988214319272273, 0.4040241417140549], Loss: 5.310067748287684
mini_batch[0]'s loss: ([[-0.977277879876411, 0.41059850193837233]], [5.310067748287684])
iter: 0, point: [-1.0000665119658712, 0.3901139032526141], Loss: 9.948974311703784
mini_batch[1]'s loss: ([[-0.988214319272273, 0.4040241417140549]], [9.948974311703784])
iter: 0, point: [-1.0099096964900296, 0.3859828997852013], Loss: 4.582071696627923
...
mini_batch[39]'s loss: ([[-1.2343588100526453, 0.14439735680045832]], [1.0128812556524254])
iter: 0, point: [-1.237167617412837, 0.1414588534395813], Loss: 0.09470445497034455
mini_batch[40]'s loss: ([[-1.236799748470745, 0.14160559639242365]], [0.09470445497034455])

2.2.4.7.2 训练过程代码修改

将每个随机抽取的 mini-batch 数据输入到模型中用于参数训练。训练过程的核心是两层循环：

1. 第一层循环，代表样本集合要被训练遍历几次，称为“epoch”，代码如下：

for epoch in range(epochs)

2. 第二层循环，代表每次遍历时，样本集合被拆分成的多个批次，需要全部执行训练，称为“iter (iteration)”，代码如下：

for iter_idx, mini_batch in enumerate(mini_batches):

在两层循环的内部是经典的四步训练流程：前向计算->计算损失->计算梯度->更新参数，这与大家之前所学是一致的，代码如下：

# 前向推理
pred = model.forward(inputs)

# 计算损失
loss = model.train(inputs, targets, interations=1, lr=0.01)

# 计算梯度
gradient_w, gradient_b = model.gradient(inputs, targets)

# 更新参数
model.update(gradient_w, gradient_b, lr=0.01)

将两部分改写的代码集成到 Network 类中的 train 函数中，最终的实现如下。

import numpy as np
import json
import matplotlib.pyplot as plt


class Network_full_weights:
    def __init__(self, num_of_weights):
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)  # 随机产生w的初始值
        self.b = 0.0  # 不使用偏置
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, pred, gt):
        loss_value_sum = (pred - gt) ** 2
        return np.mean(loss_value_sum)
    
    def gradient(self, x, gt):
        pred = self.forward(x)
        gradient_w = (pred - gt) * x
        gradient_w = np.mean(gradient_w, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = (pred - gt)
        gradient_b = np.mean(gradient_b)
        
        return gradient_w, gradient_b
    
    def update(self, gradient_w, gradient_b, lr=0.01):
        self.w = self.w - lr * gradient_w  # 负梯度，所以是减
        self.b = self.b - lr * gradient_b  # 负梯度，所以是减
        
    def train(self, inputs, epochs=100, batch_size=1, lr=0.01):
        n = len(inputs)
        losses = []
        
        for epoch in range(epochs):
            # 在每轮迭代开始之前，将训练数据的顺序随机打乱
            # 然后再按每次取batch_size条数据的方式取出
            np.random.shuffle(inputs)
            
            # 将训练数据进行拆分，每个mini_batch包含batch_size条的数据
            mini_batches = [inputs[k: k+batch_size] for k in range(0, n, batch_size)]
            
            # 对每个mini_batch进行训练
            for iter_idx, mini_batch in enumerate(mini_batches):
                x = mini_batch[:, :-1]
                gt = mini_batch[:, -1:]
                
                # infer
                pred = self.forward(x)

                # calc loss
                loss = self.loss(pred, gt)

                # record loss
                losses.append(loss)

                # calc gradients
                gradient_w, gradient_b = self.gradient(x, gt)
                
                # update weights and bias
                self.update(gradient_w, gradient_b, lr)
                
                # print
                print(f"Epoch: {
      
      epoch}\titer: {
      
      iter_idx}\tloss: {
      
      loss:.4f}")
        
        return losses


def data_load():
    # 2.2.1.1 读入数据
    datafile = "/data/data_01/lijiandong/Datasets/boston_house_price/housing.data"
    data = np.fromfile(datafile, sep=" ")


    # 2.2.1.2 数据形状变换
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)
    data = data.reshape([data.shape[0] // feature_num, feature_num])  # [N, 14]


    # 2.2.1.3 数据集划分
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]
    test_data = data[offset:]


    # 2.2.1.4 数据归一化处理
    # 计算train数据集的最大值和最小值
    maxinums, minimus = training_data.max(axis=0), training_data.min(axis=0)

    # 对数据进行归一化处理
    for col_name in range(feature_num):
        # 训练集归一化
        training_data[:, col_name] = (training_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        # 测试集归一化（确保了测试集上的数据也使用了与训练集相同的归一化转换，避免了引入测试集信息污染）
        test_data[:, col_name] = (test_data[:, col_name] - minimus[col_name]) / (maxinums[col_name] - minimus[col_name])
        
    return training_data, test_data
    
    
if __name__ == "__main__":
    # get data
    train_data, test_data = data_load()
    
    # create model
    model = Network_full_weights(13)

    # start training
    losses = model.train(train_data, epochs=100, batch_size=100, lr=0.1)
    
    # 画出损失函数的变化趋势
    plot_x = np.arange(len(losses))
    plot_y = np.array(losses)
    plt.plot(plot_x, plot_y)
    plt.xlabel("Iteration = samples num / batch size * epochs")
    plt.ylabel("Loss")
    plt.savefig("test_model_loss.png")

结果：

Epoch: 0        iter: 0 loss: 10.1354
Epoch: 0        iter: 1 loss: 3.8290
Epoch: 0        iter: 2 loss: 1.9208
Epoch: 0        iter: 3 loss: 1.7740
Epoch: 0        iter: 4 loss: 0.3366
Epoch: 1        iter: 0 loss: 1.6275
Epoch: 1        iter: 1 loss: 0.9842
Epoch: 1        iter: 2 loss: 0.9121
Epoch: 1        iter: 3 loss: 0.9971
Epoch: 1        iter: 4 loss: 0.6071
...
Epoch: 98       iter: 0 loss: 0.0662
Epoch: 98       iter: 1 loss: 0.0468
Epoch: 98       iter: 2 loss: 0.0267
Epoch: 98       iter: 3 loss: 0.0340
Epoch: 98       iter: 4 loss: 0.0203
Epoch: 99       iter: 0 loss: 0.0342
Epoch: 99       iter: 1 loss: 0.0688
Epoch: 99       iter: 2 loss: 0.0377
Epoch: 99       iter: 3 loss: 0.0317
Epoch: 99       iter: 4 loss: 0.0061

观察上述 Loss 的变化，随机梯度下降加快了训练过程，但由于每次仅基于少量样本更新参数和计算损失，所以损失下降曲线会出现震荡。

说明：

1. 由于房价预测的数据量过少，所以难以感受到随机梯度下降带来的性能提升。
2. 在机器学习中，迭代次数（Iteration）是指训练过程中更新模型参数的总次数。它由元素数（数据集中样本的数量）除以批次大小（Batch Size）再乘以训练轮数（Epoch）得出。即：$$迭代次数（\mathrm{Iteration}）=\frac{\mathrm{样本数量}}{\mathrm{BatchSize}}\times \mathrm{Epoch}$$这个公式告诉我们在整个训练过程中，模型将会更新参数多少次。训练过程会经过多个 Epoch，每个 Epoch 将数据集分成若干个批次进行训练，批次的大小由 Batch Size 决定。

2.2.5 模型保存

Numpy 提供了 save 接口，可直接将模型权重数组保存为 .npy 格式的文件。

np.save("w.npy", model.w)  # 保存模型参数
np.save("b.npy", model.b)  # 保存模型偏置

2.2.6 小结

本章我们详细介绍了如何使用 NumPy 实现梯度下降算法，构建并训练了一个简单的线性模型实现波士顿房价预测，可以总结出，使用神经网络建模房价预测有三个要点：

1. 构建网络，初始化参数 $w$ 和 $b$，定义预测和损失函数的计算方法。
2. 随机选择初始点，建立梯度的计算方法和参数更新方式。
3. 从总的数据集中抽取部分数据作为一个 mini_batch，计算梯度并更新参数，不断迭代直到损失函数几乎不再下降。

3. 使用 PaddlePaddle 重写波士顿房价预测任务

本教程中的案例覆盖计算机视觉、自然语言处理和推荐系统等主流应用场景，使用飞桨实现这些案例的流程基本一致，如下图所示。

在第二章中，我们学习了使用 Python 和 NumPy 实现波士顿房价预测任务的方法，本章我们将尝试使用飞桨重写房价预测任务，体会二者的异同。在数据处理之前，需要先加载飞桨框架的相关类库。

import paddle
from paddle.nn import Linear
import paddle.nn as nn
import paddle.nn.functional as F
import paddle.optimizer as optimizer
import numpy as np
import os
import random

代码中参数含义如下：

• paddle：飞桨的主库，paddle 根目录下保留了常用 API 的别名，当前包括：
  • paddle.tensor
  • paddle.framework
  • paddle.device
  • 目录下的所有API；
• Linear：神经网络的全连接层函数，包含所有输入权重相加的基本神经元结构。在房价预测任务中，使用只有一层的神经网络（全连接层）实现线性回归模型。
• paddle.nn：组网相关的 API，包括 Linear、卷积 Conv2D、循环神经网络 LSTM、损失函数 CrossEntropyLoss、激活函数 ReLU 等；
• paddle.nn.functional：与 paddle.nn 一样，包含组网相关的 API，如：Linear、激活函数 ReLU 等，二者包含的同名模块功能相同，运行性能也基本一致。 差别在于 paddle.nn 目录下的模块均是类，每个类自带模块参数；paddle.nn.functional 目录下的模块均是函数，需要手动传入函数计算所需要的参数。在实际使用时，卷积、全连接层等本身具有可学习的参数，建议使用 paddle.nn；而激活函数、池化等操作没有可学习参数，可以考虑使用 paddle.nn.functional。

---

说明：飞桨支持两种深度学习建模编写方式，更方便调试的动态图模式和性能更好并便于部署的静态图模式。

• 动态图模式（命令式编程范式，类比 Python）：解析式的执行方式。用户无需预先定义完整的网络结构，每写一行网络代码，即可同时获得计算结果；
• 静态图模式（声明式编程范式，类比 C++）：先编译后执行的方式。用户需预先定义完整的网络结构，再对网络结构进行编译优化后，才能执行获得计算结果。

飞桨框架 2.0 及之后的版本，默认使用动态图模式进行编码，同时提供了完备的动转静支持，开发者仅需添加一个装饰器（to_static），飞桨会自动将动态图的程序转换为静态图的 program，并使用该 program 训练并可保存静态模型以实现推理部署。

3.1 数据处理

数据处理的代码不依赖框架实现，与使用 Python 构建房价预测任务的代码相同，详细解读请参考第二章，这里不再赘述。

def load_data():
    # 从文件导入数据
    datafile = './work/housing.data'
    data = np.fromfile(datafile, sep=' ', dtype=np.float32)

    # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
                      'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)

    # 将原始数据进行Reshape，变成[N, 14]这样的形状
    data = data.reshape([data.shape[0] // feature_num, feature_num])

    # 将原数据集拆分成训练集和测试集
    # 这里使用80%的数据做训练，20%的数据做测试
    # 测试集和训练集必须是没有交集的
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]

    # 计算train数据集的最大值，最小值
    maximums, minimums = training_data.max(axis=0), training_data.min(axis=0)
    
    # 记录数据的归一化参数，在预测时对数据做归一化
    global max_values
    global min_values
   
    max_values = maximums
    min_values = minimums
    
    # 对数据进行归一化处理
    for i in range(feature_num):
        data[:, i] = (data[:, i] - min_values[i]) / (maximums[i] - minimums[i])

    # 训练集和测试集的划分比例
    training_data = data[:offset]
    test_data = data[offset:]
    return training_data, test_data
# 验证数据集读取程序的正确性
training_data, test_data = load_data()
print(training_data.shape)
print(training_data[1,:])

(404, 14)

[2.35922547e-04 0.00000000e+00 2.62405723e-01 0.00000000e+00
 1.72839552e-01 5.47997713e-01 7.82698274e-01 3.48961979e-01
 4.34782617e-02 1.14822544e-01 5.53191364e-01 1.00000000e+00
 2.04470202e-01 3.68888885e-01]

3.2 模型设计

模型定义的实质是定义线性回归的网络结构，飞桨建议通过创建 Python 类的方式完成模型网络的定义，该类需要继承 paddle.nn.Layer 父类，并且在类中定义 __init__ 函数和 forward 函数。forward 函数是框架指定实现前向计算逻辑的函数，程序在调用模型实例时会自动执行，forward 函数中使用的网络层需要在 __init__ 函数中声明。

• 定义 __init__ 函数：在类的初始化函数中声明每一层网络的实现函数。在房价预测任务中，只需要定义一层全连接层，模型结构和第二章保持一致；
• 定义 forward 函数：构建神经网络结构，实现前向计算过程，并返回预测结果，在本任务中返回的是房价预测结果。

class Regression(nn.Layer):
    def __init__(self):
        super(Regression, self).__init__()
        
        # 定义一层全连接层，输入维度是13，输出维度是1
        self.fc = nn.Linear(in_features=13, out_features=1)
        
    
    def forward(self, inputs):
        x = self.fc(inputs)
        return x

3.3 训练配置

训练配置过程如下图所示：

if __name__ == "__main__":
    # 实例化模型
    model = Regression()
    
    # 开启模型训练模式
    model.train()
    
    # 加载数据
    training_data, test_data = load_data()
    
    # 定义优化算法，使用SGD
    optimizer = optimizer.SGD(learning_rate=0.01, parameters=model.parameters())

说明：模型实例有两种状态：训练状态 .train() 和预测状态 .eval()。训练时要执行正向计算和反向传播梯度两个过程，而预测时只需要执行正向计算，为模型指定运行状态，有两点原因：

1. 部分高级的算子在两个状态执行的逻辑不同，如：Dropout 和 BatchNorm（在后续的“计算机视觉”章节会详细介绍）；
2. 从性能和存储空间的考虑，预测状态时更节省内存(无需记录反向梯度)，性能更好。

使用飞桨框架只需要设置 SGD 函数的参数并调用，即可实现优化器设置，大大简化了这个过程。

3.4 训练过程

训练过程采用二层循环嵌套方式：

• 内层循环： 负责整个数据集的一次遍历，采用分批次方式（batch）。假设数据集样本数量为 1000，一个批次有 10 个样本，则遍历一次数据集的批次数量是 1000/10=100，即内层循环需要执行 100 次。
• 外层循环： 定义遍历数据集的次数，通过参数 epochs 设置。

# 外层循环: 定义遍历数据集的次数，通过参数 epochs 设置
for epoch in range(epochs):
    ...
    # 内层循环： 负责整个数据集的一次遍历，采用分批次方式（batch）。
    for iter_idx, mini_batch in enumerate(mini_batch):
        ...

说明: batch 的取值会影响模型训练效果：

• batch 过大，会增大内存消耗和计算时间，且训练效果并不会明显提升（每次参数只向梯度反方向移动一小步，因此方向没必要特别精确）；
• batch 过小，每个 batch 的样本数据没有统计意义，计算的梯度方向可能偏差较大。

由于房价预测模型的训练数据集较小，因此将 batch 设置为 10。每次内层循环都需要执行如下图所示的步骤，计算过程与使用 Python 编写模型完全一致。

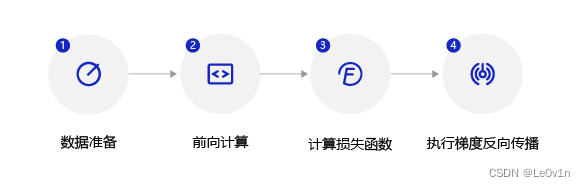
• 数据准备：将一个批次的数据先转换成 nparray 格式，再转换成 Tensor 格式；
• 前向计算：将一个批次的样本数据灌入网络中，计算输出结果；
• 计算损失函数：以前向计算结果和真实房价作为输入，通过损失函数 square_error_cost 的 API 计算出损失函数值（Loss）。
• 反向传播：执行梯度反向传播 backward 函数，即从后到前逐层计算每一层的梯度，并根据设置的优化算法更新参数(opt.step 函数)。

epochs = 100  # 总样本需要训练的轮次
batch_size = 10  # 每个 mini_batch 的样本数量

# 外层循环: 定义遍历数据集的次数，通过参数 epochs 设置
for epoch in range(epochs + 1):
    # 在每个 epoch 开始之前，将训练数据进行 Shuffle
    np.random.shuffle(training_data)
    
    # 将训练数据按照batch_size进行拆分
    mini_batches = [training_data[k: k + batch_size] for k in range(0, len(training_data), batch_size)]
    
    epoch_loss = []  # 记录损失
    
    # 内层循环： 负责整个数据集的一次遍历，采用分批次方式（mini-batch）。
    for iter_idx, mini_batch in enumerate(mini_batches):
        x = np.array(mini_batch[:, :-1])  # 训练样本
        y = np.array(mini_batch[:, -1:])  # 目标值

        # ndarray -> tensor
        inputs = paddle.to_tensor(x)
        targets = paddle.to_tensor(y)
        
        # infer
        preds = model(inputs)
        
        # calc losses
        losses = F.square_error_cost(input=preds, label=targets)
        
        # mean loss
        avg_loss = paddle.mean(losses, axis=0)
        epoch_loss.append(avg_loss.numpy())
            
        # 反向传播，计算每层参数的梯度值
        avg_loss.backward()

        # 让优化器更新参数
        optimizer.step()
        
        # 为下一个 epoch 清空当前梯度
        optimizer.clear_grad()
        
    # 打印损失
    print(f"Epoch: {
      
      epoch}\tLoss: {
      
      np.average(epoch_loss):.4f}")
    epoch_loss.clear()  # 清空历史损失

结果：

W0805 03:36:18.712543 116394 gpu_resources.cc:119] Please NOTE: device: 0, GPU Compute Capability: 7.5, Driver API Version: 10.2, Runtime API Version: 10.2
W0805 03:36:18.715507 116394 gpu_resources.cc:149] device: 0, cuDNN Version: 8.2.
Epoch: 0        Loss: 0.2431
Epoch: 1        Loss: 0.0846
Epoch: 2        Loss: 0.0774
...
Epoch: 99       Loss: 0.0133
Epoch: 100      Loss: 0.0134

和 PyTorch 是一样的，前向计算、计算损失和反向传播梯度，每个操作只需要 1 ~ 2 行代码即可实现。飞桨已经帮助我们自动实现了反向梯度计算和参数更新的过程，不再需要逐一编写代码。

3.5 保存并测试模型

3.5.1 保存模型

使用 paddle.save API 将模型当前的参数数据 model.state_dict() 保存到文件中，用于模型预测或校验的程序调用。

# 保存模型
paddle.save(obj=model.state_dict(), path="LR_model.pdparams")
print(f"模型保存成功, 路径为: LR_model.pdparams")

说明：为什么要执行保存模型操作，而不是直接使用训练好的模型进行预测？

理论而言，直接使用模型实例即可完成预测，但是在实际应用中，训练模型和使用模型往往是不同的场景。模型训练通常使用大量的线下服务器（不对外向企业的客户/用户提供在线服务）；模型预测则通常使用线上提供预测服务的服务器实现或者将已经完成的预测模型嵌入手机或其他终端设备中使用。因此本教程中“先保存模型，再加载模型”的讲解方式更贴合真实场景的使用方法。

3.5.2 测试模型

下面选择一条数据样本，测试下模型的预测效果。测试过程和在应用场景中使用模型的过程一致，主要可分成如下三个步骤：

1. 配置模型预测的机器资源。
2. 将训练好的模型参数 LR_model.pdparams 加载到模型实例中。由两个语句完成：
   1. 第一句是从文件中读取模型参数；
   2. 第二句是将参数内容加载到模型。
   • 加载完毕后，需要将模型的状态调整为 eval()（校验）。
   • 上文中提到，训练状态的模型需要同时支持前向计算和反向传导梯度，模型的实现较为臃肿，而校验和预测状态的模型只需要支持前向计算，模型的实现更加简单，性能更好。
3. 将待预测的样本特征输入到模型中，打印输出的预测结果。

我们通过 load_one_example 函数实现从数据集中抽一条样本作为测试样本，具体实现代码如下所示。

def load_one_example(test_data):
    # 从已经加载的测试集中随机选择一条作为测试数据
    idx = np.random.randint(low=0, high=test_data.shape[0])
    one_data, label = test_data[idx, :-1], test_data[idx, -1:]
    
    # 修改该条数据的shape为 [1, 13]
    one_data = one_data.reshape([1, -1])
    
    return one_data, label


# 读取模型
model_dict = paddle.load("LR_model.pdparams")
model = Regression()
model.load_dict(state_dict=model_dict)
# 转换模型状态
model.eval()
    
# 读取单条测试数据
one_data, label = load_one_example(test_data=test_data)
one_data = paddle.to_tensor(one_data)
    
# 模型推理
pred = model(one_data)
    
# 对推理结果做反归一化处理
pred = pred * (max_values[-1] - min_values[-1]) + min_values[-1]
# 对真实标签做反归一化处理
label = label * (max_values[-1] - min_values[-1]) + min_values[-1]
    
print(F"推理结果为: {
      
      pred.numpy()}\t对应的真实值为: {
      
      label}")

结果：

推理结果为: [[16.670935]]       对应的真实值为: [13.6]

通过比较“模型预测值”和“真实房价”可见，模型的预测效果与真实房价接近。房价预测仅是一个最简单的模型，使用飞桨编写均可事半功倍。那么对于工业实践中更复杂的模型，使用飞桨节约的成本是不可估量的。同时飞桨针对很多应用场景和机器资源做了性能优化，在功能和性能上远强于自行编写的模型。

4. PaddlePaddle 与 PyTorch 语法区别

4.1 前向传播：一样

"""=============== PyTorch ==============="""
# 前向传播
loss = model(input_data, target)


"""=============== Paddle ==============="""
# 前向传播
loss = model(input_data, target)

4.2 反向传播：一样

"""=============== PyTorch ==============="""
loss.backward()


"""=============== Paddle ==============="""
# 反向传播
loss.backward()

4.3 更新参数：一样

"""=============== PyTorch ==============="""
# 定义优化器
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

# 更新参数
optimizer.step()


"""=============== Paddle ==============="""
# 定义优化器
optimizer = paddle.optimizer.SGD(learning_rate=learning_rate, parameters=model.parameters())

# 更新参数
optimizer.step()

4.4 清空梯度：不一样

"""=============== PyTorch ==============="""
# 清空梯度
optimizer.zero_grad()


"""=============== Paddle ==============="""
# 清空梯度
optimizer.clear_gradients()

4.5 模型参数文件及模型后缀：一样

"""=============== PyTorch ==============="""
# 保存模型参数
torch.save(model.state_dict(), "model.pt")  # 后缀一般是 .pt 或 .pth


"""=============== Paddle ==============="""
# 保存模型参数
paddle.save(model.state_dict(), "model.pdparams")  # 后缀一般是 .pdparams

4.6 读取模型：不一样

"""=============== PyTorch ==============="""
# 加载模型参数
model_state_dict = torch.load("model.pt")
model.load_state_dict(model_state_dict)


"""=============== Paddle ==============="""
# 加载模型参数
model_state_dict = paddle.load("model.pdparams")
model.set_state_dict(model_state_dict)

知识来源

1. https://www.paddlepaddle.org.cn/tutorials/projectdetail/3520300
2. https://www.paddlepaddle.org.cn/tutorials/projectdetail/5836960
3. https://www.paddlepaddle.org.cn/tutorials/projectdetail/4309126