傅里叶变换 是啥?
傅里叶变换是以法国数学家让-巴蒂斯特·约瑟夫·傅里叶(Jean-Baptiste Joseph
Fourier)的名字命名的,以纪念他对这一数学工具的贡献。傅里叶生活在18世纪末和19世纪初,他是一位多才多艺的科学家,不仅在数学领域有杰出的成就,还在热传导、天体物理学等领域做出了重要贡献。
傅里叶变换最早的形式是由傅里叶于1822年首次引入的,他在其著作《解热方程的解析法》中描述了将周期函数分解为一系列正弦和余弦函数的方法。他的工作为现代信号处理、图像处理和其他领域中的频域分析奠定了基础。
傅里叶变换之所以以傅里叶的名字命名,是因为他是第一个系统地研究和应用这一数学工具的人。傅里叶的工作深刻影响了现代科学,尤其在信号处理、图像处理和通信等领域,傅里叶变换被广泛应用于分析和处理不同类型的信号和数据。
傅里叶变换中的变换是变换什么?
在傅里叶变换中,"变换"指的是将一个函数从时域(时间域)表示转换为频域(频率域)表示。换句话说,傅里叶变换将一个函数的表达方式从描述其在不同时间点的行为,转换为描述其在不同频率上的成分。
在傅里叶变换中,我们要对一个函数(通常是信号或图像)进行变换。这个函数可以是连续的,也可以是离散的。连续傅里叶变换(CFT)适用于连续时间信号,将其从时域转换为连续频率域。离散傅里叶变换(DFT)适用于离散时间信号,将其从时域转换为离散频率域。
在opencv 中变换的什么?
在 OpenCV 中,傅里叶变换(Fourier Transform)是对图像进行的变换,将图像从空间域(时域)转换为频率域。具体来说,OpenCV
中的傅里叶变换是离散傅里叶变换(DFT),用于将离散图像从时域转换为离散频率域。
在傅里叶变换中,OpenCV 对输入的图像进行数学变换,将图像的每个像素表示为一系列正弦和余弦波的振幅和相位。这样可以将图像从其原始像素表示转换为表示图像中不同频率成分的复杂表示。
看了上面的信息还是不知道是个啥,就知道为什么叫傅里叶变换
傅里叶变换非常抽象,很多人在工程中用了很多年的傅里叶变换也没有彻底理解傅里叶变换到底是怎么回事。为了更好地说明傅里叶变换,我们先看一个生活中的例子。
表 14-1 所示的是某饮料的配方,该配方是一个以时间形式表示的表格,表格很长,这里仅仅截取了其中的一部分内容。该表中记录了从时刻“00:00”开始到某个特定时间“00:11”内的操作。
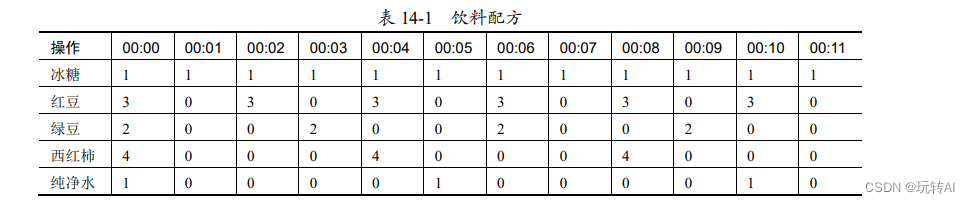
仔细分析该表格可以发现,该配方:
- 每隔 1 分钟放 1 块冰糖。
- 每隔 2 分钟放 3 粒红豆。
- 每隔 3 分钟放 2 粒绿豆。
- 每隔 4 分钟放 4 块西红柿。
- 每隔 5 分钟放 1 杯纯净水。
上述文字是从操作频率的角度对配方的说明。
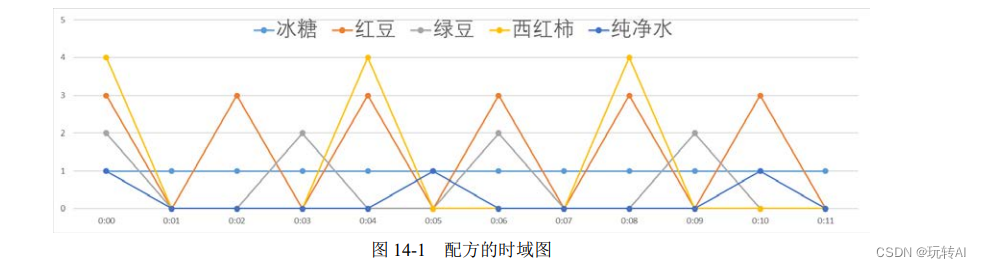
在数据的处理过程中,经常使用图表的形式表述信息。如果从时域的角度,该配方表可以表示为图 14-1。图 14-1 仅仅展示了配方的前 11 分钟的操作,如果要完整地表示配方的操作,必须用图表绘制出全部时间内的操作步骤。
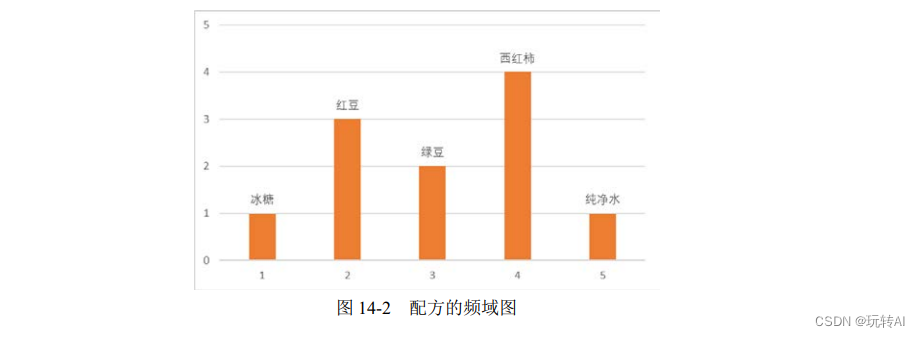
如果从频率(周期)的角度表示,这个配方表可以表示为图 14-2,图中横坐标是周期(频率的倒数),纵坐标是配料的份数。
可以看到,图 14-2 可以完整地表示该配方的操作过程。
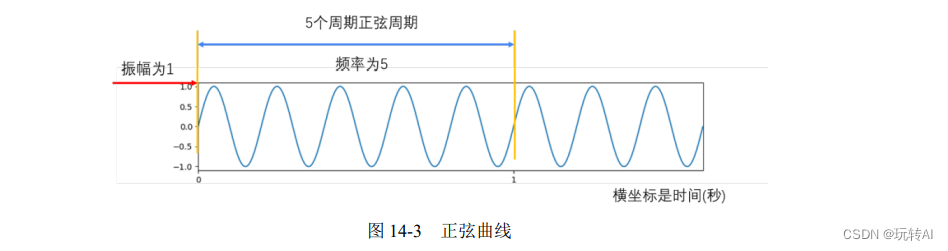
对于函数,同样可以将其从时域变换到频域。
图 14-3 是一个频率为 5(1 秒内 5 个周期)、振幅为 1 的正弦曲线。
如果从频率的角度考虑,则可以将其绘制为图 14-4 所示的频域图,图中横坐标是频率,纵坐标是振幅。
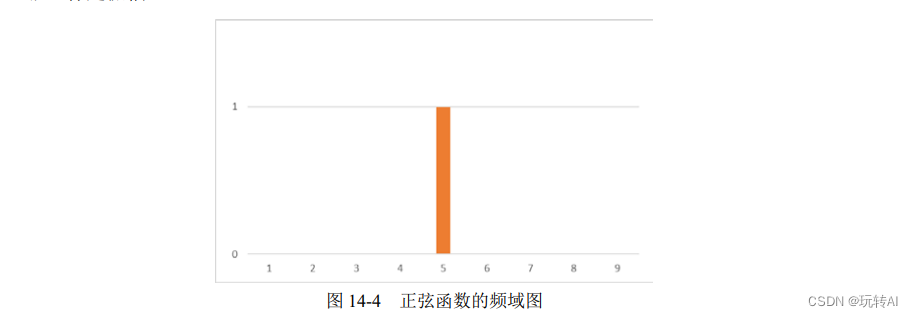
14-3 与图 14-4 是等价的,它们是同一个函数的不同表示形式。可以通过频域表示得到对应的时域表示,也可以通过时域表示得到对应的频域表示。
法国数学家傅里叶指出,任何周期函数都可以表示为不同频率的正弦函数和的形式。在今天看来,这个理论是理所当然的,但是这个理论难以理解,在当时遭受了很大的质疑。
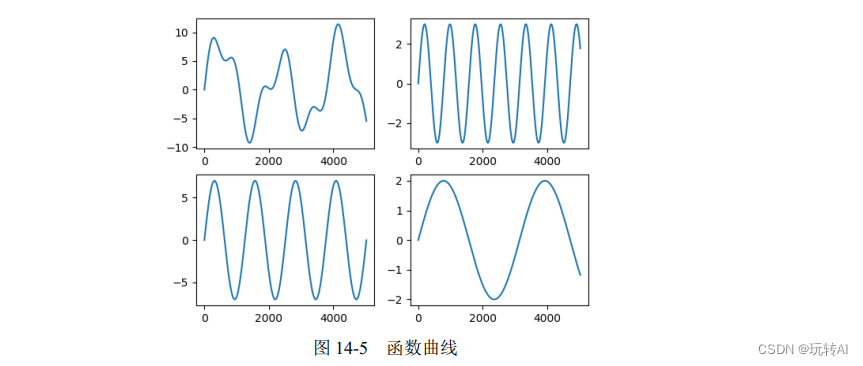
下面我们来看傅里叶变换的具体过程。例如,周期函数的曲线如图 14-5 左上角的图所示。该周期函数可以表示为:
y = 3np.sin(0.8x) + 7np.sin(0.5x) + 2np.sin(0.2x)
因此,该函数可以看成是由下列三个函数的和构成的:
- y1 = 3np.sin(0.8x) (函数 1)
- y2 = 7np.sin(0.5x) (函数 2)
- y3 = 2np.sin(0.2x) (函数 3)
上述三个函数对应的函数曲线分别如图 14-5 中右上角、左下角及右下角的图所示。
如果从频域的角度考虑,上述三个正弦函数可以分别表示为图 14-6 中的三根柱子,图中横坐标是频率,纵坐标是振幅。
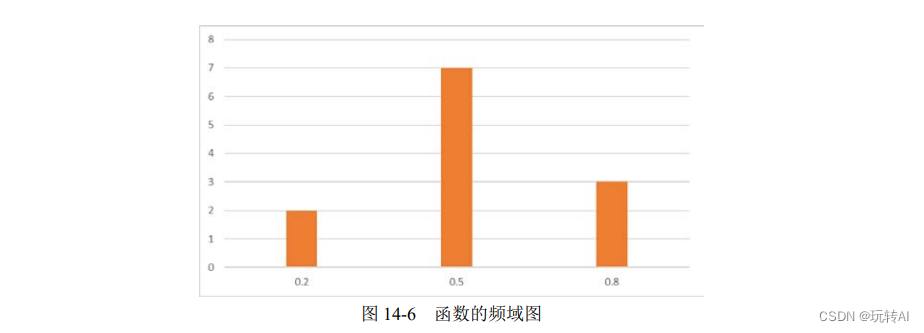
通过以上分析可知,图 14-5 中左上角的函数曲线可以表示为图 14-6 所示的频域图。
从图 14-5 左上角的时域函数图形,构造出如图 14-6 所示的频域图形的过程,就是傅里叶变换。
图 14-1 与图 14-2 表示相同的信息,图 14-1 是时域图,而图 14-2 是频域图。
图 14-5 左上角的时域函数图形,与图 14-6 所示的频域图形表示的页是完全相同的信息。
傅里叶变换就是从频域的角度完整地表述时域信息。
除了上述的频率和振幅外,还要考虑时间差的问题。例如,饮料配方为了控制风味,需要严格控制加入配料的时间。表 14-1 中“00:00”时刻的操作,在更精细的控制下,实际上如表14-2 所示。
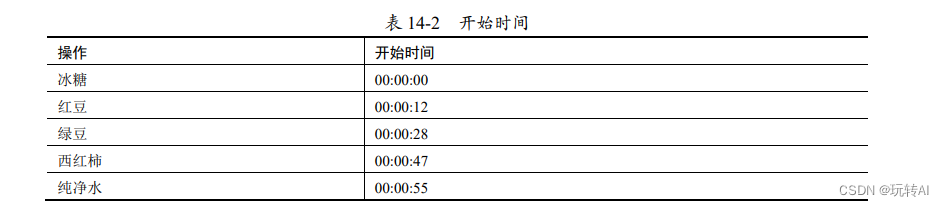
如果加入配料的时间发生了变化,饮料的风味就会发生变化。所以,在实际处理过程中,还要考虑时间差。这个时间差,在傅里叶变换里就是相位。相位表述的是与时间差相关的信息。
例如,图 14-7 中左上角图对应的函数可以表示为:
y = 3np.sin(0.8x) + 7np.sin(0.5x+2) + 2np.sin(0.2x+3)
因此,该函数可以看成是由下列 3 个函数的和构成的:
- y1 = 3np.sin(0.8x) (函数 1)
- y2 = 7np.sin(0.5x+2) (函数 2)
- y3 = 2np.sin(0.2x+3) (函数 3)
上述 3 个函数对应的函数曲线分别如图 14-7 中右上角、左下角和右下角的图所示。
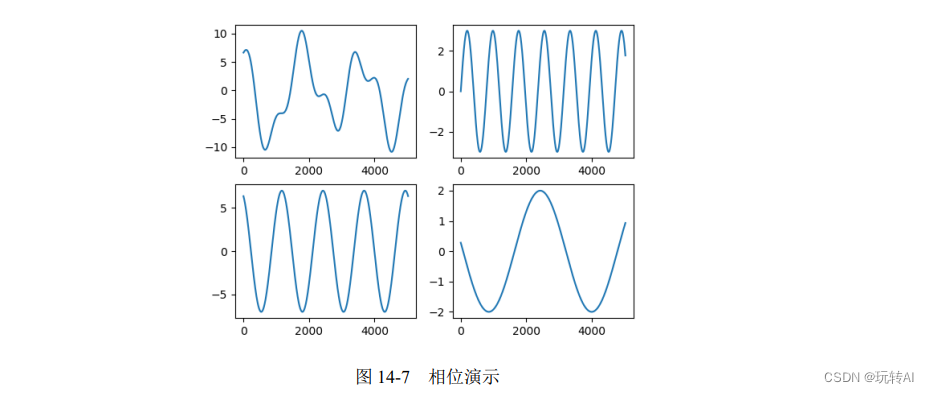
在本例中,如果把横坐标看成开始时间,则构成函数 y 的三个正弦函数并不都是从 0 时刻开始的,它们之间存在时间差。如果直接使用没有时间差的函数,则无法构成图 14-7 左上角图所示的函数,而是会构成图 14-5 左上角图所示的函数。
所以,相差也是傅里叶变换中非常重要的条件。
上面分别用饮料配方和函数的例子介绍了时域与频域转换的可行性,希望对大家理解傅里叶变换能有所帮助。
在图像处理过程中,傅里叶变换就是将图像分解为正弦分量和余弦分量两部分,即将图像从空间域转换到频率域(以下简称频域)。数字图像经过傅里叶变换后,得到的频域值是复数。
因此,显示傅里叶变换的结果需要使用实数图像(real image)加虚数图像(complex image),或者幅度图像(magnitude image)加相位图像(phase image)的形式。
因为幅度图像包含了原图像中我们所需要的大部分信息,所以在图像处理过程中,通常仅使用幅度图像。当然,如果希望先在频域内对图像进行处理,再通过逆傅里叶变换得到修改后的空域图像,就必须同时保留幅度图像和相位图像。
对图像进行傅里叶变换后,我们会得到图像中的低频和高频信息。低频信息对应图像内变化缓慢的灰度分量。高频信息对应图像内变化越来越快的灰度分量,是由灰度的尖锐过渡造成的。
例如,在一幅大草原的图像中有一头狮子,低频信息就对应着广袤的颜色趋于一致的草原等细节信息,而高频信息则对应着狮子的轮廓等各种边缘及噪声信息。
傅里叶变换的目的,就是为了将图像从空域转换到频域,并在频域内实现对图像内特定对象的处理,然后再对经过处理的频域图像进行逆傅里叶变换得到空域图像。傅里叶变换在图像处理领域发挥着非常关键的作用,可以实现图像增强、图像去噪、边缘检测、特征提取、图像压缩和加密等。
看着一堆文字说明 烧脑子,下面看看代码
Numpy 实现傅里叶变换函数说明
Numpy 模块提供了傅里叶变换功能,Numpy 模块中的 fft2()函数可以实现图像的傅里叶变换。
Numpy 提供的实现傅里叶变换的函数是 numpy.fft.fft2(),它的语法格式是:
返回值 = numpy.fft.fft2(原始图像)
这里需要注意的是,参数“原始图像”的类型是灰度图像,函数的返回值是一个复数数组(complex ndarray)。
经过该函数的处理,就能得到图像的频谱信息。此时,图像频谱中的零频率分量位于频谱图像(频域图像)1的左上角,为了便于观察,通常会使用numpy.fft.fftshift()函数将零频率成分移动到频域图像的中心位置,如图 14-8 所示。
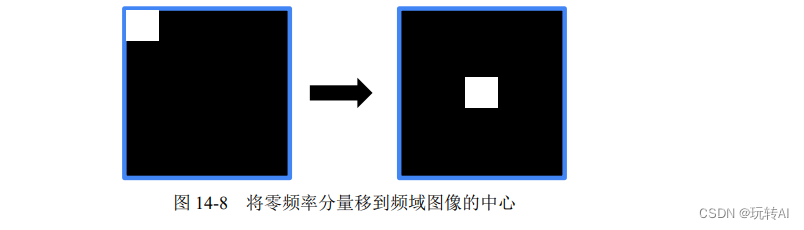
函数 numpy.fft.fftshift()的语法格式是:
返回值=numpy.fft.fftshift(原始频谱)
使用该函数处理后,图像频谱中的零频率分量会被移到频域图像的中心位置,对于观察傅里叶变换后频谱中的零频率部分非常有效。
对图像进行傅里叶变换后,得到的是一个复数数组。为了显示为图像,需要将它们的值调整到[0, 255]的灰度空间内,使用的公式为:
像素新值=20*np.log(np.abs(频谱值))
代码示例:用 Numpy 实现傅里叶变换,观察得到的频谱图像。
代码如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))
plt.subplot(121)
plt.imshow(img, cmap = 'gray')
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show()
运行结果:
显示原始图像和其频谱图像

实现逆傅里叶变换
需要注意的是,如果在傅里叶变换过程中使用了 numpy.fft.fftshift()函数移动零频率分量,那么在逆傅里叶变换过程中,需要先使用 numpy.fft.ifftshift()函数将零频率分量移到原来的位置,再进行逆傅里叶变换,该过程如图 14-10 所示。
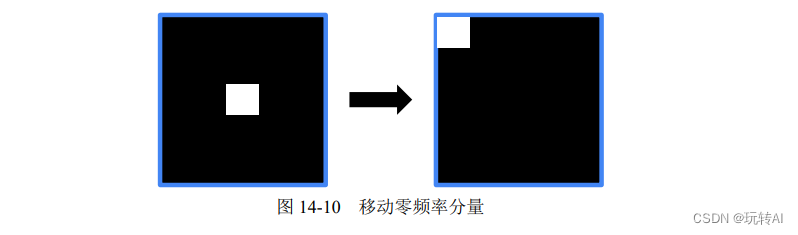
函数 numpy.fft.ifftshift()是 numpy.fft.fftshift()的逆函数,其语法格式为:
调整后的频谱 = numpy.fft.ifftshift(原始频谱)
numpy.fft.ifft2()函数可以实现逆傅里叶变换,返回空域复数数组。它是 numpy.fft.fft2()的逆函数,该函数的语法格式为:
返回值=numpy.fft.ifft2(频域数据)
函数 numpy.fft.ifft2()的返回值仍旧是一个复数数组(complex ndarray)。
逆傅里叶变换得到的空域信息是一个复数数组,需要将该信息调整至[0, 255]灰度空间内,使用的公式为:
iimg = np.abs(逆傅里叶变换结果)
示例:在 Numpy 内实现傅里叶变换、逆傅里叶变换,观察逆傅里叶变换的结果图像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
#对图像进行傅里叶变换,结果是复数
f = np.fft.fft2(img)
#将低频部分移动到图像中心
fshift = np.fft.fftshift(f)
#将复数变化成实数
magnitude_spectrum = 20*np.log(np.abs(fshift))
#将傅里叶变换的结果进行反变换
ishift = np.fft.ifftshift(fshift)
#对傅里叶变换的结果进行反变换
iimg = np.fft.ifft2(ishift)
#取绝对值
iimg = np.abs(iimg)
plt.subplot(131),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(132),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('magnitude_spectrum'),plt.axis('off')
plt.subplot(133),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()
运行结果:

高通滤波示例
在一幅图像内,同时存在着高频信号和低频信号。
- 低频信号对应图像内变化缓慢的灰度分量。例如,在一幅大草原的图像中,低频信号对
应着颜色趋于一致的广袤草原。 - 高频信号对应图像内变化越来越快的灰度分量,是由灰度的尖锐过渡造成的。如果在上面的大草原图像中还有一头狮子,那么高频信号就对应着狮子的边缘等信息。
滤波器能够允许一定频率的分量通过或者拒绝其通过,按照其作用方式可以划分为低通滤波器和高通滤波器。
- 允许低频信号通过的滤波器称为低通滤波器。低通滤波器使高频信号衰减而对低频信号放行,
会使图像变模糊。 - 允许高频信号通过的滤波器称为高通滤波器。高通滤波器使低频信号衰减而让高频信号通过,将增强图像中尖锐的细节,但是会导致图像的对比度降低。
傅里叶变换可以将图像的高频信号和低频信号分离

要将图 14-12 中右图中间的像素值都置零,需要先计算其中心位置的坐标,然后选取以该坐标为中心,上下左右各 30 个像素大小的区域,将这个区域内的像素值置零。
该滤波器的实现方法为:
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
示例:在 Numpy 内对图像进行傅里叶变换,得到其频域图像。然后,在频域内将低频分量的值处理为 0,实现高通滤波。最后,对图像进行逆傅里叶变换,得到恢复的原始图像。
观察傅里叶变换前后图像的差异。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
rows, cols = img.shape
crow,ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'),plt.axis('off')
plt.show()
运行结果:

OpenCV 实现傅里叶变换
OpenCV 提供了函数 cv2.dft()和 cv2.idft()来实现傅里叶变换和逆傅里叶变换,下面分别展开介绍。
实现傅里叶变换
函数 cv2.dft()的语法格式为:
返回结果=cv2.dft(原始图像,转换标识)
在使用该函数时,需要注意参数的使用规范:
- 对于参数“原始图像”,要首先使用 np.float32()函数将图像转换成 np.float32 格式。
- “转换标识”的值通常为“cv2.DFT_COMPLEX_OUTPUT”,用来输出一个复数阵列。
函数 cv2.dft()返回的结果与使用 Numpy 进行傅里叶变换得到的结果是一致的,但是它返回的值是双通道的,第 1
个通道是结果的实数部分,第 2 个通道是结果的虚数部分。
经过函数 cv2.dft()的变换后,我们得到了原始图像的频谱信息。
此时,零频率分量并不在中心位置,为了处理方便需要将其移至中心位置,可以用函数 numpy.fft.fftshift()实现。
例如,如下语句将频谱图像 dft 中的零频率分量移到频谱中心,得到了零频率分量位于中心的频谱图像 dftshift。
dftShift = np.fft.fftshift(dft)
经过上述处理后,频谱图像还只是一个由实部和虚部构成的值。要将其显示出来,还要做进一步的处理才行。
函数 cv2.magnitude()可以计算频谱信息的幅度。该函数的语法格式为:
返回值=cv2.magnitude(参数 1,参数 2)
式中两个参数的含义如下:
- 参数 1:浮点型 x 坐标值,也就是实部。
- 参数 2:浮点型 y 坐标值,也就是虚部,它必须和参数 1 具有相同的大小(size 值的大小,不是 value 值的大小)。
函数 cv2.magnitude()的返回值是参数 1 和参数 2 的平方和的平方根,公式为:
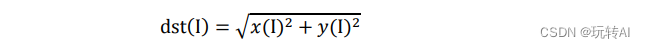
式中,I 表示原始图像,dst 表示目标图像。
得到频谱信息的幅度后,通常还要对幅度值做进一步的转换,以便将频谱信息以图像的形式展示出来。简单来说,就是需要将幅度值映射到灰度图像的灰度空间[0, 255]内,使其以灰度图像的形式显示出来。
这里使用的公式为:
result = 20*np.log(cv2.magnitude(实部,虚部))
下面对一幅图像进行傅里叶变换,帮助读者观察上述处理过程。如下代码针对图像“lena”进行傅里叶变换,并且计算了幅度值,对幅度值进行了规范化处理:
import numpy as np
import cv2
img = cv2.imread('lena.png',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
print(dft)
dftShift = np.fft.fftshift(dft)
print(dftShift)
result = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))
print(result)
得到的值范围分别如图 14-14 所示。其中:
- 左图显示的是函数 cv2.dft()得到的频谱值,该值是由实部和虚部构成的。
- 中间的图显示的是函数 cv2.magnitude()计算得到的频谱幅度值,这些值不在标准的图像灰度空间[0, 255]内。
- 右图显示的是对函数 cv2.magnitude()计算得到的频谱幅度值进一步规范的结果,现在值的范围在[0, 255]内。

示例:用 OpenCV 函数对图像进行傅里叶变换,并展示其频谱信息
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
result = 20*np.log(cv2.magnitude(dftShift[:,:,0],dftShift[:,:,1]))
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'),plt.axis('off')
plt.subplot(122),plt.imshow(result, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()
运行结果:
- 左图是原始图像。
- 右图是频谱图像,是使用函数 np.fft.fftshift()将零频率分量移至频谱图像中心位置的结果。

实现逆傅里叶变换
在 OpenCV 中,使用函数 cv2.idft()实现逆傅里叶变换,该函数是傅里叶变换函数 cv2.dft()
的逆函数。其语法格式为:
返回结果=cv2.idft(原始数据)
对图像进行傅里叶变换后,通常会将零频率分量移至频谱图像的中心位置。如果使用函数
numpy.fft.fftshift() 移动了零频率分量, 那 么 在进行逆傅里叶变换前,要使用函数
numpy.fft.ifftshift()将零频率分量恢复到原来位置。
还要注意,在进行逆傅里叶变换后,得到的值仍旧是复数,需要使用函数 cv2.magnitude()
计算其幅度。
示例:用 OpenCV 函数对图像进行傅里叶变换、逆傅里叶变换,并展示原始图像及经过逆傅里叶变换后得到的图像。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('lena.png',0)
#对图像进行傅里叶变换
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
#将低频部分移动到图像中心
dftShift = np.fft.fftshift(dft)
#将复数变化成实数
ishift = np.fft.ifftshift(dftShift)
#将傅里叶变换的结果进行反变换
iImg = cv2.idft(ishift)
#取绝对值,取对数的目的为了将数据变化到较小的范围(比如0-255),并显示,结果是复数
iImg= cv2.magnitude(iImg[:,:,0],iImg[:,:,1])
print(iImg.shape)
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122),plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()
运行结果:

右图是对原始图像 img 进行傅里叶变换、逆傅里叶变换后得到的图像。