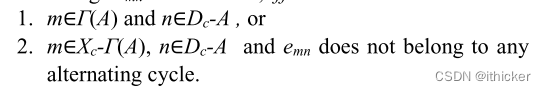Abstract—摘要
不同的约束是大多数约束满足问题的重要组成部分。已知不同约束的广义弧一致性问题可以归结为一个值图中的最大匹配问题。 在值图的任何最大匹配中都没有出现的冗余边可以而且应该从图中删除。 现有的方法试图通过在找到图的最大匹配后计算强连通分量来识别这些冗余边。 本文给出了一个新的冗余边识别定理。 我们证明了在找到一个最大匹配后可以立即检测出一些冗余边缘。 基于这一理论结果,我们提出了一种处理不同约束的有效算法。 实际问题的实验结果表明,新算法的性能明显优于现有的算法。
一. 导言
约束规划是解决问题的有力工具,在现实世界的各种应用中得到了广泛的应用。约束满足问题(CSP)定义了一组变量,这些变量的值必须满足某些指定的约束。 最有用和最重要的约束之一是AllDifferent约束[Lauriere1978],它要求约束的所有变量必须具有不同的值。 各种不同的约束可以在各种各样的组合问题中找到[Wallace1996],包括各种谜题、图着色和指派问题。
求解CSP的典型方法是从所有可能的变量值中搜索。 为了加速这个搜索过程,引入了各种一致性技术来从不属于问题任何解决方案的变量域中删除值。 Régin提出了一种适用于各种约束的广义弧一致性(GAC)的经典滤波算法。 该算法利用图论C.Berge[Berge and Minieka,1973]的一个定理,对所有不同约束的值图的最大匹配中不出现的冗余边进行剪枝。 对于不同约束一致性的弱形式,Leconte[Leconte1996]提出了一种基于Hall区间识别的距离一致性算法。 Puget[Puget1998]提出了一种比值域一致性更弱的边界一致性算法。 据我们所知,Régin算法仍然是最先进的GAC滤波方法。 Gent[Gent,Miguel et al.2008]讨论了Régin算法的几个实现细节,特别是残差图的强连通分量(SCC)的计算。 在[Van Hoeve2001]中可以找到对所有不同约束的调查。 近年来,AllDifferent约束作为一种强大的工具,被广泛应用于求解困难的约束优化问题,如子图同构[Solnon2010]和约束聚类[Duong and Vrain2017]。
本文提出了一种简单而快速的求解各种不同约束的算法。 我们的新算法是基于一个新的定理来识别所有不同约束的值图的冗余边。 本文将冗馀边分为两类:一类冗馀边可以通过寻找最大匹配立即得到,另一类冗馀边可以通过计算小的子图中的SCCs得到。 基于这个定理,我们设计了一个有效的算法来求解各种不同的约束。 我们算法的主要改进来自于1型冗余边的识别,这使得我们可以在不增加任何计算的情况下去除大量的冗余边。 与先进方法相比,新算法不需要构造残差图,残差图的边比原值图的边多。 因此,我们算法中的SCCS计算也比以前的算法快。 我们使用Minion1.8软件[Gent,Jefferson et al.]对新算法在许多基准实例上的性能进行了评估,结果表明我们的算法在所有问题实例上的性能都优于Régin算法。
论文的组织方式如下。 我们在第2节中介绍了与约束满足问题和图论有关的定义。 在第3节中,我们提出并证明了一个新的值图冗余边识别定理,并给出了一个适用于各种约束的快速算法。 我们在第4节中评估了算法在几个实际问题上的性能,并在第5节中进行了讨论。
二. 背景和初步情况
1. 约束定义: 约束满足问题(CSP)是一个三元组(x,d,c),其中x是一组变量,{x1,x2,…,xn},d是一组域{d1,d2,…,Dn},其中di是变量xi的可能值集,c是变量之间的约束集。 Csp(x,d,c)的解是一组值(d1,…,dn)∈D1×··×dn,其中,对于变量xi1,…,xim上的每一个约束c∈C,我们有(di1,…,dim)∈C。 一个约束是广义弧一致的(GAC),即每个变量的值都可以扩展到约束的所有其他变量,这样约束就满足了。
2. An alldifferent constraint: C(x1,…,xn)是一个约束,它指定对于任何i<j,xi≠xj。 对于一个完全不同的约束C,二部图B©=(xc,dc,e)称为C的值图,其中(xi,d)∈E iff d∈DI。 为了在不同的约束条件下实现GAC,需要引入图论中的一些概念,特别是关于最大匹配的概念。
3. 图论 考虑一个二分图B(U,V,E),其中U,V是两个不相交的节点集,E中的每条边都将U中的一个节点连接到V中的一个节点。
- 匹配是一组没有公共节点的边集。
- 如果节点连接到匹配中的边,则称为匹配节点,否则称为自由节点。
- 边数最大的匹配称为最大匹配。
- 交替路径是指其边在匹配中和匹配中是交替的路径。 增广路径是两端节点为自由节点的交替路径。
一个二分图可能有多个最大匹配,因此最大匹配通常不是唯一的。 对于一个图,可能存在许多相同大小的最大匹配。 允许的边是属于某些(但不是全部)最大匹配的边。 冗余边是指不出现在任何最大匹配中的边。 类似地,允许的节点是由一些(但不是全部)最大匹配覆盖的节点。
4. Régin’s滤波算法。 在B©[Régin1994]中,一个完全不同的约束是GAC,它的值图的每条边都属于覆盖XC的匹配。 因此,要实现GAC,需要去除其值图中的冗余边。 Régin[Régin1994]提出了一种基于以下性质的滤波算法:
性质1(Berge1970):对于任意最大匹配M,允许边属于从自由结点开始的偶数交替路径或偶数交替循环。
因此,为了识别值图的所有冗余边,该算法首先计算一个最大匹配,然后基于SCCS找到所有从自由节点开始的交替路径和所有偶数的交替循环。 最后两个步骤可以通过在有向残差图中寻找SCCs来结合。 残差图是通过在原值图上增加一个虚节点和DC边来构造的。 因此,残差图总是大于值图。 残差图的独立SCC之间的不匹配边(即free边)是冗余边。 一个例子如图1所示。

三. 识别冗余边缘
对于一个完全不同的约束C,对应于任何最大匹配中从未出现的边的变量-值对应该被剪枝。 因此,在本文的其余部分,我们将重点讨论如何有效地识别值图的所有冗余边。
考虑一个完全不同的约束C(Xc,Dc)和它的值图B(c)=(Xc,Dc,E)。
- 设A是B(c)的允许结点集
- Γ(A)是A的邻居结点集。
显然,如果存在约束解,Xc的所有结点都必须匹配。 因此,允许的节点只能在集合Dc中找到。 该值图的节点集可分为A、Γ(A)、Dc-A、Xc-Γ(A)四个集合。 允许的节点很容易被我们以前的工作[Zhang,Han et al.2017]识别出来,最初用于识别一个网络的输入节点。
Xc的所有结点都必须匹配,在值图当中覆盖Xc的匹配等价于最大匹配,所以对于所有最大匹配一定包含Xc内所有值,允许的节点是由一些(但不是全部)最大匹配覆盖的节点,Xc的节点是全部最大匹配覆盖的节点,故不为允许节点,所以许的节点只能在集合Dc中找到。对于集合Dc当中寻找允许节点即分为允许和不允许节点两部分A、Dc-A。而Xc和Dc通过边相连且边仅在两节点集合之间,集合内无边,则Dc中的邻居节点均在Xc中,所以A的邻居节点都在Xc中即为Γ(A),Xc其余节点则为Xc-Γ(A)。
性质2: 允许结点IFF 对于任意最大匹配M(提出最大匹配M是为了确定matching和free边进一步确定交替的路径),该结点可以通过从自由结点开始的偶数交替路径到达。
基于性质2,并使用我们的节点集划分,我们现在给出了一个新的识别冗余边的定理: 、
定理: 对于任意最大匹配,不匹配的边EMN是冗余的 IFF
证明: 根据A,Γ(A),Dc-A和Xc-Γ(A)的定义,一个值图的边可以分为E(Γ(A),A),E(Γ(A),Dc-A)和E(Xc-Γ(A),Dc-A)三个集合(图2)。 注意,基于Γ(a)的定义,A的所有邻居节点都应该在Γ(a)中。Xc-Γ(A)是 Xc中与A有边连接节点以外节点,因此,在A和xc-Γ(A)之间不存在边。
我们首先证明了E(Γ(a),a)的所有边都是允许边
- 自己理解:允许的节点是由一些(但不是全部)最大匹配覆盖的节点,则允许节点对应的边均是由一些(但不是全部)最大匹配覆盖的边,允许节点的边均与Γ(a)连接,则E(Γ(a),a)的所有边都是允许边。
- 一个非匹配边Eba∉M,其中a∈A和b∈Γ(a)。 因为A是一个允许的节点,所以根据属性2,必须存在一个偶数交替的路径P连接节点A和自由节点。 考虑路径P+Eba,如果我们交换路径的匹配边和不匹配边,我们有一个新的最大匹配M′,其中Eba∈M′。 因此,E(Γ(a),a)的所有边都是允许边,并且可以在新的最大匹配M′中。
其次,我们证明了E(Γ(A),Dc-A)的所有边都是冗余的。 因为Γ(a)是变量集的一部分,所以Γ(a)的任何节点都应该匹配。否则,就无法解决约束。- 首先Γ(a)属于Xc,Xc中的节点一定属于最大匹配,则所有节点一定应该匹配
- 同时开始证明了E(Γ(a),a)是允许边,一个边是允许边在 Régin’s滤波算法中提出当且仅当改边属于某些max matching不是所有,故该节点一定匹配
设Emn是允许边,其中m∈Γ(A),n∈Dc-A。 由于Γ(A)是A的邻居集,且A的任意节点都是允许的,因此必然存在一条从连接到节点M的自由节点开始的交替路径P。 因此,路径p+Emn是一个交替路径。 基于属性2,节点n是允许的节点。 这与节点N的定义相矛盾。 因此,E(Γ(A),Dc-A)的所有边都是冗余边。
最后,我们证明了E(Xc-Γ(A),Dc-A)的边是冗余边,它们不匹配,不属于任何交替循环。 注意,它是性质1的推论。 因此,证明完成了。
图2给出了上述定理的一个简单例子。 在找到值图的最大匹配(红边)之后,节点5是唯一空闲的节点。 允许的节点集为A={3,4,5},因为节点3和4可以通过从节点5开始的交替路径到达。 A的邻集为Γ(a)={x3,x4}。 根据我们的定理,集合Γ(A)与DC-A之间的边可以从值图中去除(1)性质。 因此,我们只需要找到集合{x1,x2}和{1,2}之间的不匹配边,而不是在任何交替循环中(2)性质这就是边E(x2,1)。
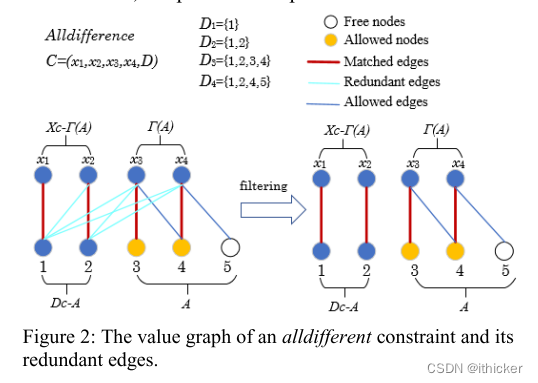
评价:对于值图的简化即去除冗余边的效果暂时是等价的,效率感觉有所提高,首先两种方法都需要最大匹配算法,原来需要全局遍历寻找cycle和path,而现在我们只需要遍历free node寻找path由于性质2确定allowed node 从而获得A、Γ(A)、Dc-A、Xc-Γ(A)四个集合,根据定理我们去除冗余边,效率大大提升。
这个定理给我们提供了一种在二部图中寻找冗余边的有效方法。 根据该定理,节点集Γ(A)与DC-A之间的边用1型冗余边表示,其余冗余边用2型冗余边表示。
- 在找到允许节点集后,可以很容易地得到第1类冗余边。 允许的节点可以通过查找基于属性2的最大匹配来找到。最大匹配算法如Hopcroft-Karp算法[Hopcroft and Karp1973]或Hungarian算法[Kuhn1955]的基本思想是迭代寻找与手头匹配M对应的所有增广路径,然后导出更大的匹配M′。 当不能找到增广路径时,获得最大匹配, 该算法的最后一步就是从最大匹配的空闲节点开始寻找所有的交替路径。 因此,在一个最大匹配算法的最后一步可以得到所有允许的节点及其邻居,该算法提供了第一部分冗余边。
- 对于剩余的冗余边,我们只需要在一个较小的子图B′(XC-Γ(A),DC-A,E′)中找到SCCs,其中E′-是连接XC-γ(A)和DC-A的边集。
上述思想和步骤在算法1中得到体现,用于对不同约束条件的值图B进行过滤。


我们的算法的第一部分是寻找最大匹配,这可以通过Hopcroft-Karp算法在O(|Xc|0.5|E|)中完成。 第二部分是求二部图B′(XC-Γ(A),DC-A,E′)的SCC,这可以用Tarjan算法[Tarjan1972]在O(Xc-Γ(A)+Dc-A+E′)中完成。 虽然我们的算法具有与前人相同的最坏情况复杂度,但在实际应用中具有更好的性能。 这是因为在找到一个最大匹配后,许多冗余边可以立即被去除,并且我们只需要在一个较小的图B′(XC-Γ(a),DC-a,E′)中寻找SCCs,而不是在原始值图中寻找SCCs。
算法1的第一部分(步骤1-10)基本上是寻找一个最大匹配。 因此,它可以与许多最大匹配算法相结合,如Hopcroft-Karp算法或Hungarian算法。 此外,我们的算法的改进是在匹配过程中识别出1型冗余边,因此,它可以结合许多优化技术来解决不同的约束条件,如增量匹配、域计数、优先级队列、分阶段传播或独立计算SCCs[Gent,Miguel et al.2008]。
四. 实验结果
我们评估了新算法的性能。我们首先分析了所有冗余边中类型 1 冗余边的比例。然后,我们将我们的算法的性能与针对所有不同约束的大量基准实例的最先进方法进行了比较。 我们的算法是基于 Minion constraint solver 1.8 [Gent, Jefferson et al.] 实现的。所有实验都在 Windows 7 工作站上运行,该工作站配备 3.9 GHz 的四核 Intel i7-3770 处理器和 32GB DDR3 1600MHz RAM。
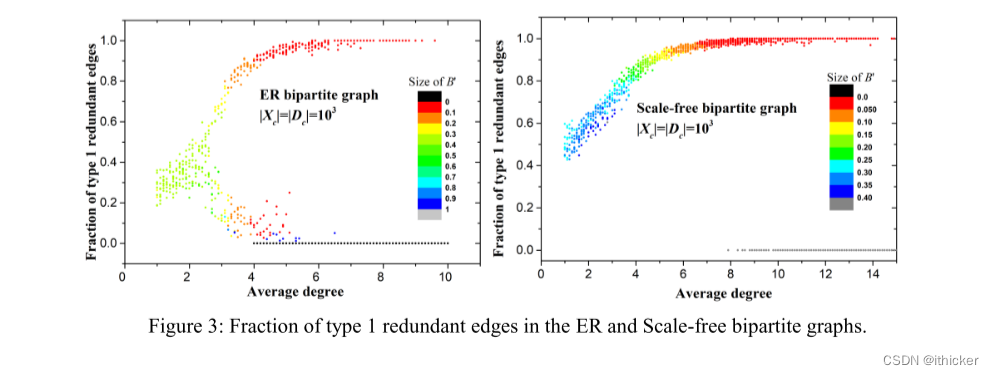
在我们的实验中,我们首先使用[Shen-Orr,Milo et al.2002]的无标度网络模型和[Bollobás2013]的ER随机网络模型生成了一系列合成二分图,其中我们设置Xc=Xc=1000。 类型1冗余边可以在最大匹配后获得。 因此,如果有更多的第1类边,我们的算法将更加高效。 当平均节点度增加时,冗余边大多为1型,且B′(XC-Γ(A)、DC-A、E′)的大小相对较小(图3)。 这意味着在找到一个最大匹配后,可以找到大部分冗余边,剩下的冗余边可以在一个小值图B′(xc-γ(a),Dca,E′)中得到。 这将大大提高算法在实际应用中的效率。 我们还评估了一些实际问题中1型冗余边的比例(图4)。 计算了搜索过程中冗余边的总数,并计算了1型和2型冗余边的比例。 很明显,许多问题也有很大一部分类型1冗余边。

接下来,我们使用 Minion 软件 1.8 版 [Gent, Jefferson et al.] 实现了我们的新算法。该软件已经实现了 Régin 的 [Régin 1994] 过滤算法和其他优化技术,例如增量匹配 [Régin 1994]、BFS 匹配 [Cormen 2009] 和分阶段传播 [Schulte 和 Stuckey 2004]。为了实现我们的算法,我们使用 Hopcroft–Karp 算法来获得最大匹配和 Tarjan 算法来计算 SCC。我们还使用增量匹配技术,这与 [Régin 1994] 相同。 我们将我们的算法与以下实现进行了比较:
1)Régin 的增量匹配过滤算法(IncMatch)
2)IncMatch使用FF-BFS匹配算法代替Hopcroft-Karp算法(IncMatchBFS)
3)IncMatch-BFS 分阶段传播 (IncMatchBFS-Staged)。
**我们用来解决问题的搜索策略是深度优先时间顺序回溯。**基准实例选自 [Gent, Miguel et al. 2008],包括兰福德数问题(CSPLib 中的 prob024 [Gent 和 Walsh 1999])、哥伦布标尺问题(CSPLib 中的 prob006)、带孔的平衡拟群 (QWH) [Kautz、Ruan 等人。 2001]、类群存在(CSPLib 中的 prob003)、社交高尔夫球手(CSPLib 中的 prob010)、优雅图(CSPLib 中的 prob053)、N-Queens(CSPLib 中的 prob054)和运动调度。
在这些约束满足问题的实例中,我们将我们的算法与上述三种现有方法进行了比较。在实验中,我们将时间限制为 4 小时,将节点限制为 106 个。对于那些可以在时间限制内找到解决方案的问题,我们比较了原始运行时间(图 5 和表 1)。对于那些超过时间限制的问题,我们统计了每秒搜索的节点数(图 6)。 如表 1 和图 5-6 所示,我们的算法绝不会比其他算法慢,并且通常比这些方法快 1-6 倍。重申一下,我们算法的效率提升来自识别和删除类型 1 约束,计算量很小。在那些没有 1 型冗余边的问题上,我们的算法也有更好的性能,因为它在值图中找到 SCC,而不是在残差图中找到 SCC,残差图比原始值图有更多的边。



五 结论
我们开发了一种快速过滤算法,用于实现 alldifferent 约束的广义弧一致性。我们提出了一个新的定理,用于识别约束图中需要删除的冗余边。我们表明,我们的算法在我们测试的所有基准问题上明显优于最佳 GAC 算法,显着减少了这些实际问题的计算时间。我们的算法可用于提高解决包含所有不同约束的约束满足问题的性能。