摘要- ABSTRACT
AllDifferent约束是任何约束工具包、语言或求解器的重要组成部分，因为它被广泛应用于各种约束模型中。 文献中包含了这个约束的许多不同版本，它们以推断的强度与计算成本进行交易。 在这篇文章中，我们关注于推理的最高强度，加强了一个称为广义弧一致性(GAC)的性质。 本文对GAC的主要算法在AllDifferent约束条件下的优化进行了分析研究。 我们从文献中对一些关键技术进行了实证评估。 我们还报告了这些技术的重要实现细节，这些细节通常在已发表的论文中没有描述。 我们特别关注通过利用在标准传播过程中发现的强连接组件来改进增量，因为这以前没有详细说明。 我们的经验工作代表了迄今为止对AllDifference的GAC算法变体的最广泛的一组实验。 总体而言，优化的最佳组合在没有优化的情况下给出了相同实现168倍的平均加速。
引言
在工业和学术界的许多领域，约束是一种强大而自然的知识表示和推理手段。 例如，考虑一个大学时间表的制作。 这一问题的制约因素包括：数学报告厅可容纳100名学生； 艺术史讲座需要一个有幻灯机的场地； 任何学生都不能同时参加两次讲座。 一个组合问题的约束求解分两个阶段进行。 首先，将问题建模为一组决策变量，以及一组解决方案必须满足的对这些变量的约束条件。 决策变量表示为了解决问题必须做出的选择。 与每个决策变量相关联的潜在值域对应于该选择的选项（选择的选项就是变量的取值）。 在我们的例子中，每个讲座可能有两个决策变量，分别代表时间和地点。 对于每一班学生来说，他们上课的时间变量可能对他们有一个不同的限制，以确保课程不会同时在两个地方进行。 第二阶段包括使用约束求解器搜索解：为满足所有约束的决策变量赋值。 这种方法的简单性和通用性是将约束求解成功应用于许多学科的基础，如调度、工业设计和组合数学[29]。
AllDifferent约束表示变量向量取不同的值。 它是任何约束系统的重要组成部分，广泛应用于各种约束模型中，如拟群的构造和完成、运动调度、时间表和Golomb标尺的构造等。 文献中包含了这个约束的许多不同版本，它们以推断的强度与计算成本进行交易。 事实上，选择适当的一致性水平有时对于有效地解决CSP是至关重要的[26]。 Van Hoeve考察了推论的各种力量[28]，包括6.1.2节中描述的弱的和快速的成对分解，界和范围一致性，以及广义弧一致性(GAC)。 Régin[21]给出了求解AllDifferent约束的经典GAC算法。 在本文中，我们关注的是推理的最高强度（强制GAC）。 将自己限制在GAC允许我们深入研究各种优化，但这意味着本文的范围不包括边界和范围一致性算法的优化。
本文是对广义弧一致性(GAC)的主要算法在不同约束条件下的优化问题的分析综述。 当基于对已发表的优化的调查，我们从三个方面扩展了文献。
- 首先，我们提供了我们所讨论的优化的广泛实现细节。 最初的出版物经常省略这些细节，例如出于篇幅的原因。 提供这样的细节应该可以避免未来的工人不得不重新发明轮子。
- 其次，我们提供了广泛的实证分析，以显示我们所调查的技术的价值或其他。 重要的是，我们能够相互结合地评估优化。
- 第三，我们详细介绍了以前文献中没有描述过的技术，以及我们在这里介绍的一些新技术。 在前一类中，我们展示了如何在搜索过程中探索强连接组件中的增量。 在后一类中，我们介绍了使用动态触发器减少必要传播数量的方法，以及对变量赋值情况的优化。
在本文的第二节中，我们回顾了关键的背景资料，在较高的水平上介绍了Régin算法，并综述了文献中对其提出的优化。 我们讨论了增量匹配、域计数、优先队列的使用、分阶段传播、独立处理强连通分量、重要边、顾问和不动点推理。（贡献二）
第三节给出了算法的具体实现。 对关键实施问题的详细调查是本文的贡献之一。 （贡献1）
在第4节中，我们详细介绍了如何利用强连通分量来提高各种传播的效率。 在Régin算法中，我们在一个由允许的值和变量与值之间的匹配构成的图中找到了一组SCCs。 不同的SCCs之间的边表示不可能的值。 当我们向下移动搜索树中的一个分支时，SCC只能保持不变或分裂成新的SCC。 因此，当我们删除一个变量-值对时，我们只需要研究包含被删除的变量-值对的单个SCC。 由于这可能只包含原始约束中所有变量的一小部分，我们可以大大减少这种增量传播所需的工作量。 本文首次详细介绍了这一技术，因为它以前一直存在于民间传说中，而不是文学作品中。 （贡献三前一类技术） 我们在第6节中实证表明这是一个非常有价值的优化。 我们还给出了进一步的，次要的，优化对SCCS的计算，对于我们把一个变量赋给一个值的常见情况。
在第5节中，我们将展示如何利用GAC AllDifferent的“动态触发器”。 在标准算法中，当任何值被删除时，我们必须做一些工作。 Katriel证明了存在一小组变量-值对，这样，如果删除任何其他值，就不可能传播[16]，并给出了一个概率算法来利用这一思想。 我们将这一思想扩展到一种技术，它在减少传播者被调用的次数的同时，确定地保持GAC。 这可以使用动态触发器在Minion中实现[10]。 事实上，我们在AllDifferent Propagator内部实现动态触发器的版本上显示了略微更好的性能。 这有一个额外的优点，即它可移植到没有动态触发器基础结构的求解器。 我们在第5节中给出了全部细节，在第6.4节中给出了实验结果。 我们的结论是，这项技术主要是在GAC所有不同的表现不好的情况下有益的，所以它可能不是普遍有用的。 （贡献三后一类技术）
我们在第6节中的经验工作代表了迄今为止关于AllDifferent的GAC算法变体的最广泛的一组实验。 我们实现了我们所调查的大部分（尽管不是全部）优化。 实现基于最先进的Minion约束求解器[9]。 我们的比较从来不与稻草人实现相比，因为所有技术都使用相同的实现，除了添加优化或用另一种技术替换一种技术。 我们的结果提出了一些观点。 在某些情况下，我们确认了文献中关于如何实现GAC AllDifferent的标准建议。 我们在第6.3节中展示了增量匹配可以减少运行时间，并且作为一个昂贵的约束，所有AllDifferent约束应该在一个单独的队列中传播，在传播便宜的约束之后。 同时，我们还证明了将GAC AllDifferent算法和一个更便宜的算法结合成一个混合阶段传播器是值得的。 针对文献中已有的建议，我们证明了一个简单的匹配算法比一个复杂的匹配算法更有效。 而且，尽管以前没有文献报道过，但我们表明开发强连接组件特别有益，平均加速率约为3倍。 我们在第7节中总结了我们对未来实施者的建议。
与Régin算法的简单实现相比，我们最好的技术组合总是比不使用它们好，可以将搜索速度提高数千倍。 我们得到的平均加速比香草实现168倍。 我们希望我们的调查将帮助其他实现者在他们的系统中获得这些加速，并刺激研究人员发明更有效的优化。
2. 背景
2.1. 准备工作
虽然我们定义约束CK的作用域为xk1，…，xkr，但在讨论特定的约束时，我们经常省略k下标，并将变量称为x1，…，xr，而将域称为d1，…，dr。
图论
Régin的Allvarif算法[21]利用了图论的结果，特别是最大二部匹配[3]和强连通分量[27]。
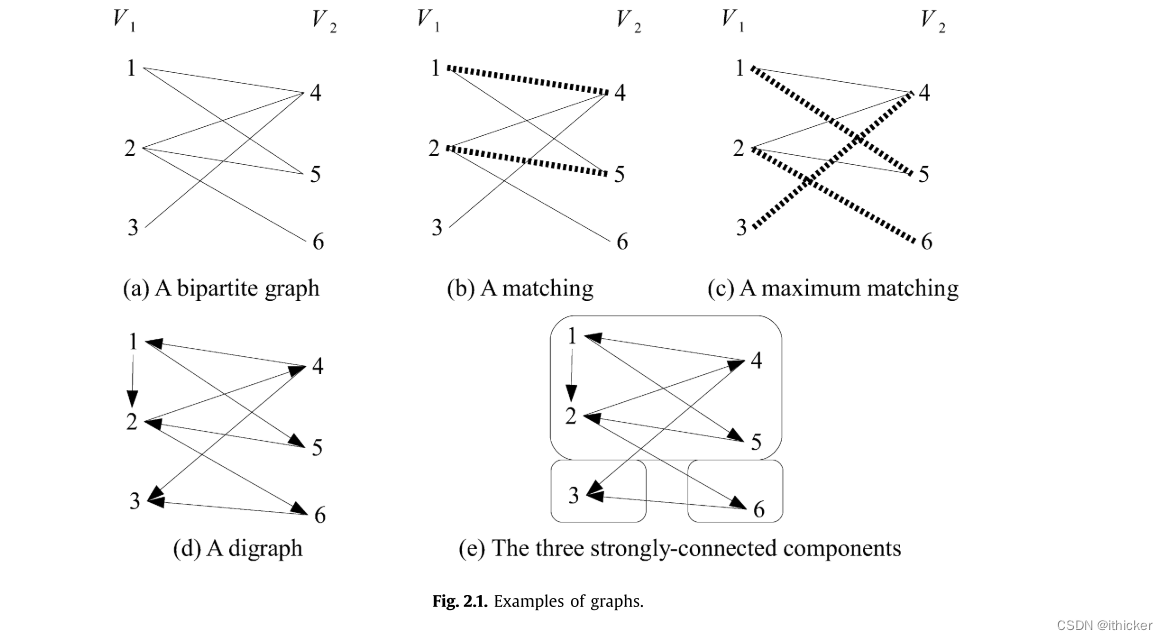
我们考虑二部图和有向图。 二部图G=<V,E>定义为一组顶点V和一组边E ⊆ V×V,其中边被解释为没有方向，没有重复的边，并且顶点可以划分为两个集合V1和V2，使得同一集合中没有两个元素相邻。 图 2.1(a)给出了一个二部图的例子，其中V1={1,2,3}和V2={4,5,6}。
二部图的一个匹配是一组边M ⊆ E，使得没有两条边连接到同一个顶点。 图 2.1(b)给出了基数为2的匹配的一个例子，其中粗体、虚线边缘在匹配中。 最大匹配（也称为最大基数匹配）是具有最大基数的匹配。 图 2.1©给出了示例二分图的最大匹配。 在这种情况下，最大匹配是唯一的。 有许多算法可以计算二分图中的最大匹配，例如Hopcroft-Karp[14]和Ford-Fulkerson[6]。
有向图也是一组顶点V上的一对G=<V，E>,一组边E V×V。边被解释为有方向。 图 2.1(d)给出了一个有向图的例子。 强连通分量(SCC)是有向图的极大顶点集，具有从任意顶点到任意顶点的路径的性质。 因此，SCCs内有循环，SCCs之间没有循环的边。 SCCs集合形成有向图顶点的一个分区。 Tarjan算法可以在线性时间内有效地计算任意有向图的SCCs[27]。 为图 2.1(d)，3个SCC分别为{1,2,4,5}，{3}和{6}，如图所示 2.1(e).
2.2. Régin和Costa算法
正如Knuth和Raghunathan[18]所指出的，众所周知，寻找“不同代表”系统的问题等价于二部匹配。 在约束求解方面，Régin[21]利用这种等价性构造了适用于各种约束的经典GAC算法。 Costa同时发表了一个非常相似的算法[7]。 Régin算法具有较好的时间限制。 从这里开始，我们只考虑Régin的算法。
该算法使用图论的结果，特别是Berge[3](CH.7，第125页）的一个定理，在一个有两个主要阶段的算法中：寻找变量到不同值的最大匹配，以及寻找有向图的强连通分量。 算法通常是增量式的，但为了简单起见，我们将其概括为非增量式的：
- 从变量到不同值找到一个最大有效匹配M。 Hopcroft-Karp[14]或Ford-Fulkerson[6]算法可用于此。
- 当|M|<r时，约束是不可满足的。（r是变量个数，最大匹配无法覆盖Xc，存在变量无合理取值，无解）
- 由M和变量域构造残差图R。 该有向图具有R的强连通分量之间的边对应于可剪枝的文字（变量-值对就是边，连通分量之间的非匹配边是冗余边，也不会有匹配边，若边属于某个匹配则一定在某个path或者cycle中即有向残差图中的连通分量）的性质。 R定义如下（定义2.2）。
- 计算R.Tarjan算法[27]的强连通分量。
- 修剪G中对应边横贯两个SCC，且不包含在M.2中的变量-值对
2.2.1. 算法的非正式描述
计算匹配
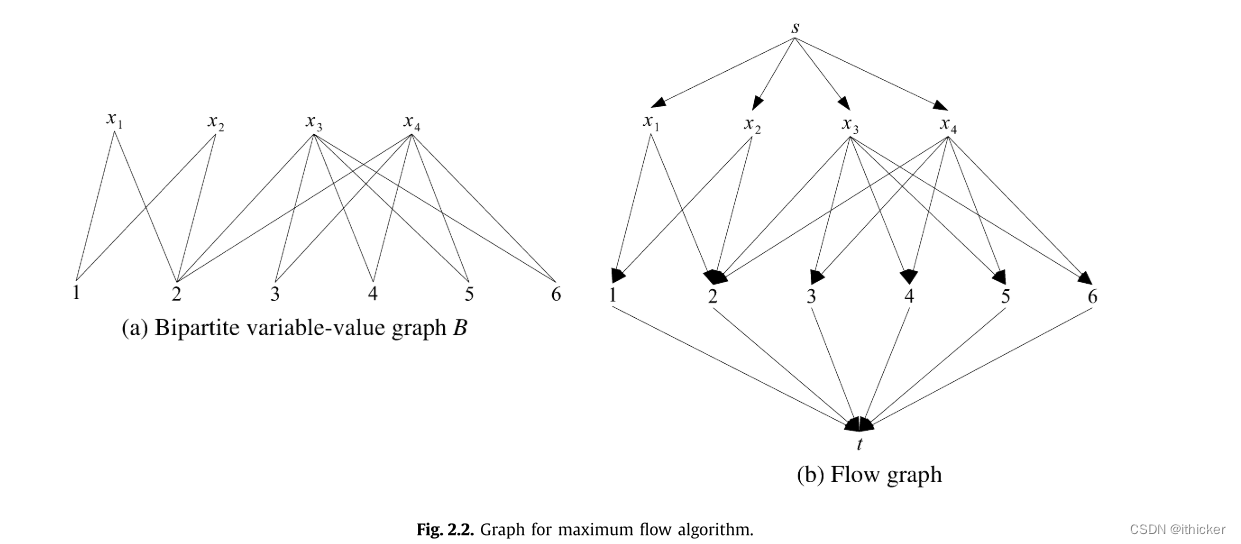
二部变量-值图如图所示 2.2(a). 每个变量由一个顶点表示，每个值由一个顶点表示，并且变量XI和值J由边连接，如果J在XI的域中。 该图表示为B。上述算法的第一阶段是在该图中构造一个最大匹配。
我们可以把二部最大匹配问题看作是一个有向图中的最大流问题。 最大流量是指在不违反边界容量限制的情况下，沿着有向图的边缘，寻找一种材料可以从源顶点运送到汇聚点的最大速率的问题。 有向图是由B通过添加一个源顶点S和一个汇点T来构造的。 边集如下所示：S对所有变量x1.…x4，每个值1.…6对汇点t，B中的每个边被翻译成从变量顶点到值的有向边。 这就产生了图如图表 2.2(b)，我们称之为流图。 为了找到最大流量，每个边的容量为1。
Ford-Fulkerson方法[6]（第27章）可用于求从S到T的流图中的最大流，该算法可求出一条增广路径，即可以用来增加流的路径。 例如，S→X1→1→T在图是一条增广路径 2.2(b). 该算法采用增广路径来增加流量，并计算出第二个流图。 在第二流图中寻找第二增广路径，以这种方式Ford-Fulkerson迭代地找到并应用增广路径，直到不存在这样的路径。 因此，有一系列的流图，在最后的流图中达到顶点，该流图表示从S到T的最大流。
任何流图的每个边要么在从S到T的流中使用，要么不使用。 未使用的边可以沿着第一个流图中的边的方向携带大小为1的新流。 相反，使用过的边缘可以携带相反方向的新流，并变得不使用。 因此，在所有流图中，所用边的方向相对于它们在第一流图中的方向是相反的。
当应用扩展路径时，路径中的每个已使用的边都变得未使用，反之亦然。 这样做的效果是反转路径中所有边的方向，以创建序列中的下一个流图。
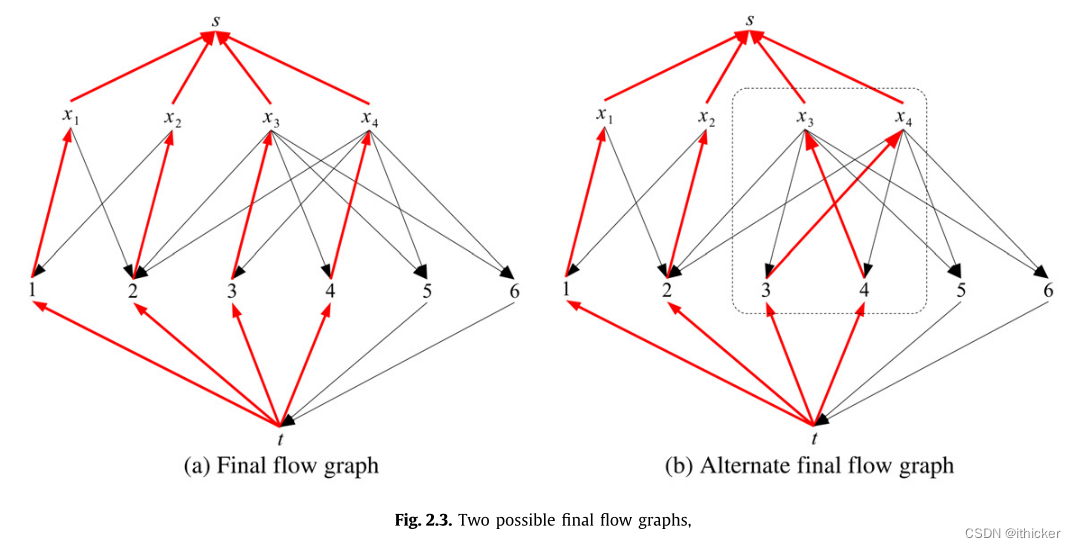
一个可能的最终流程图显示在图 2.3(a)，表示所有i∈1…r.的匹配xi=i。最后的流图表示一个最大匹配，该匹配用于AllDifferent算法的下一阶段。
此时，算法必须测试最大匹配是否覆盖所有变量。 如果不是，那么约束就不能满足，因为每个变量都必须赋值（上面算法的第2行）。
计算SCCS
考虑一下图 2.3(a)再次。 如果我们在这个图中取任意一个圈，把它的所有边的方向反向，那么我们就有了另一个流图，它表示一个不同的最大匹配。 例如，如果循环t→4→x4→5→t是反向的，我们将匹配中x4的赋值改为5。 反转循环3→X3→4→X4→3对应于匹配中的交换值3和4。 这与Ford-Fulkerson算法的一次迭代非常相似，不同之处在于从S到T的流保持不变，因为路径在同一个顶点开始和结束。 对于旋回3→x3→4→x4→3，图给出了旋回反转的结果 2.3(b).
通过在最终的流图中找到循环，并反转循环中的所有边，可以产生所有的最大匹配[3]（第7章，第124-125页）。 在Berge语言中，包含t的循环对应于从一个非饱和顶点开始的交替初等偶链。 不包括t的循环对应于交替的初等循环。
在图 2.3(a)，两个集合S1={x1,x2,1,2}和S2={x3,x4,3,4,5,6,t}是不同的，因为没有包含这两个集合顶点的圈。 换句话说，S1中的变量不能在S2中取值，反之亦然。 事实上，S1和S2是SCCs（如2.1节所定义）。 两条边(X3→2,X4→2)从一个SCC到另一个SCC交叉。
最后的流图被划分为SCCs。 为图 2.3，SCs为S1={x1,x2,1,2},S2={x3,x4,3,4,5,6,T},S3={s}。 对于从一个SCC交叉到另一个SCC的任何边，并且不包含在匹配中，它对应的域值被删除。 这足以强制执行GAC[21]。 在这个例子中，由于边X3→2和X4→2，从X3和X4的域中移除2。
2.2.2. 详细介绍了AllDifferent算法
为了构造一个完善的GAC算法[21]，Régin利用了Berge的一个结果，该结果应用于B：允许边（属于一些，但不是全部的最大匹配）iff 边属于偶数（包含偶数个边）且从不匹配顶点开始交替（该路径在匹配中的边与非边之间交替）的路径，或交替循环[3](CH.7，第125页）。 既不允许也不在匹配中的边不在最大匹配中（not allowed and not vital），并且对应于因此可以剪枝的变量-值对。 我们现在详细描述Régin算法。
在上面的非正式描述中，我们使用Ford-Fulkerson算法来计算匹配，其最终残差图用于算法的第二阶段。 Ford-Fulkerson可能不是最有效的匹配算法，所以在本节中我们将匹配从SCC计算中分离出来。
所有区域的并集的大小为|D1 ∪ ··· ∪ Dr|= d。 为了简单起见，域元素被假定为1…d。
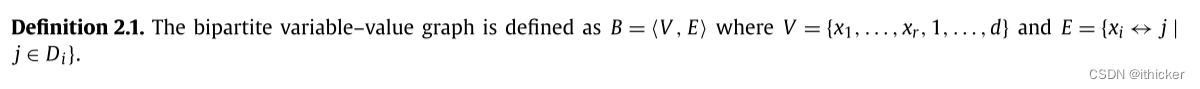
对B应用二部匹配算法，返回最大基数匹配M：{x1,…,xr}→{1,…,d}。 如果m<r，则AllDifferent约束不可满足（最大matching无法覆盖Xc则证明有变量无法取值），算法返回false。
接下来我们构造残差有向图作为M和D1…Dr的函数。 这类似于最后的流图，只是我们省略了源顶点S，因为它总是一个单例SCC，并且每个边的方向是相反的（出于效率考虑，这不影响SCCS）。
将SCC算法应用于R,返回V’（scc节点）的分区S={S1,…,SK},若K=1,则该算法结束。 否则，对于B中不包含在M中的、连接S中两个SCC中顶点的每个边，该边对应于一个被剪枝的变量-值对。
2.3. 基本算法的优化
许多作者对基本算法提出了一些优化。 我们在这里调查他们。
2.3.1. 增量匹配
匹配的M可以在搜索期间增量地保持[21]。 Régin建议在调用之间存储变量值图和匹配中涉及的边集的表示。 删除的边缘将在回溯超过导致其删除的决定时恢复。 与修剪值相对应的边将增量地移除。 为了去除适当的边，Régin的算法要求将一组去除的值传递到传播器中。
若采用Hopcroft-Karp算法进行匹配修复，Régin将Hopcroft-Karp算法和所有不同算法的时间复杂度从O(r^1.5d)提高到O(√krd)，其中k为丢失的匹配边数[21]3
2.3.2. 域计数
Quimper和Walsh[20]提出了集合、多集合和元组变量的AllDifferent和全局基数约束的变体。 这些变量类型可以有非常大的域。 他们观察到，如果变量Xi的定义域大于某个阈值，那么约束不需要通过对Xi的任何剪枝来触发。 阈值总是小于或等于r。 Quimper和Walsh给出了一个算法，在构造一组域小于其阈值的变量之前，计算所有域的大小。 虽然这一思想是在集合、多集合和元组变量的背景下提出的，但它也可以适用于小的有限域。
我们怀疑计算所有域将是昂贵的。 在我们的实验中，我们遵循Lagerkvist和Schulte[19]的更简单的方法，它使用R作为阈值。 当变量事件触发约束时，将计算变量的域DI。 如果If |Di | < r,则调用传播程序（或排队等待调用）。
我们观察到阈值可以降低到R-1。 原始引理[20]基于霍尔集，其中霍尔集是变量集H，使得每个变量域是值集DH的子集，并且|DH|=H。 如果存在一个Hall集，那么DH中的所有值都从H中不存在的所有变量中剪枝；如果所有Hall集都被找到并执行相应的剪枝，那么GAC就建立了。 大小为r的霍尔集是没有用的，因为在霍尔集之外没有要剪枝的变量。 有用的最大霍尔集的大小为r-1，其中所有域的大小为r-1或更小。 因此，在我们的域计数实验中，只有当Di |改变且|Di | < r时，才调用（或排队等待调用）传播子。
作为霍尔集的一个例子，考虑以下AllDifference约束:X1…X3∈{1…3}，X4…X6∈{3…6}：AllDifference(X1…X6)， 变量x1.…x3形成一个霍尔集，DH值集为{1.…3}。 因此，值3从变量x4…x6的域中移除。 这种类型的推理被非正式地用于解决数独谜题。
2.3.3. 优先级队列
许多约束求解器都有约束的优先级队列[1,15,23]，这样优先级就决定了约束传播器的执行顺序。 AllDifferent约束具有低优先级是标准做法。 Schulte和Stuckey证明了优先级排队的重要性[22]，并在我们的实验中对其进行了评估。
2.3.4. 分阶段传播
Schulte和Stuckey还提出了多重或分级传播[22]，其中具有高优先级的廉价传播器与更昂贵的低优先级传播器相结合。 对于包含所有不同的实例，这种方法显示了一些希望，因此我们在实验中评估了一个分阶段传播器。
2.3.5. AllDifference的分解
例如，假设我们有AllDifference(x1…x6)，并且有x1…x3∈{1…3}，x4…x6∈{4…6}。 这可以分解成独立的约束AllDifference(x1…x3)和AllDifference(x4…x6)。 如果我们能有效地发现和管理分解，这种分解可以节省时间。 不幸的是，这种优化是在社区的民间传说中而不是在文献中。分解约束的一个廉价方法是使用GAC AllDifferent算法找到的强连通分量。 正如我们在第4节中所报告的，这种方法并不完整（它没有找到所有可能的分解），但它在实践中工作得很好。 如何有效地管理分解还不是很明显。 本文的贡献之一是在第4节中描述了如何有效地实现这种优化，包括算法和数据结构。
2.3.6. 重要边
Katriel观察到，许多的值移除影响AllDifferent不会导致其他值移除，因此处理它们的工作是浪费的[16]。 在基于网络流的约束的更一般的上下文中，她引入了“重要边缘”的概念。 一个重要的边是这样一个边，它的移除会导致一些变量-值对的移除。 她给出了所有AllDifferent和普遍基数约束的重要边数的上界。 如果图足够稠密（即如果每个变量有许多允许的值），她表明只通过间歇传播就可以降低传播的预期成本。 她建议，当影响约束的值移除的简单计数达到一个数字时，触发传播，该数字表明，在概率上，一个值可能被删除。 请注意，该算法实际上并不强制执行GAC，因为当计数较低时，它可能会错过传播，而是在搜索树中较深的节点捕获它们。 Katriel没有报告实现，并观察到未能传播的风险可能超过传播的降低成本。
虽然Katriel算法的实现很有趣，但它不维护GAC的事实使它超出了本文的范围。 在本文中，我们采用了重要边的概念来减少所有不同传播子被调用的次数，同时仍然保证了GAC的正确执行。 我们通过使用“动态触发器”[10]来实现这一点，并在第5节中详细报告这一点。 我们描述了一种廉价的技术，用于最多找到2R+D边，使得任何不在集合中的边都被保证不是重要边。
2.3.7. 文献中的其他建议
Lagerkvist和Schulte在Gecode求解器的上下文中开发advisors[19]。 Advisor是在变量事件发生时立即执行的过程。 他们使用Advisors和AllDifferent来实现域计数，并在违反匹配时热切地维护匹配。 不幸的是，对于他们试验的所有不同的变体和问题实例，advisors的成本超过了他们的好处[19]。 我们没有用advisors做实验。
Schulte和Stuckey提出了不动点推理[22]，并观察到他们的实例Golomb-10-D在运行时有了非常轻微（0.1%）的改进，该实例具有GAC AllDifferent约束。 不动点推理可以通过消除无用的调用来减少对传播者的调用次数。 然而，他们观察到AllDifferent算法的无用执行是廉价的，由于它的增量做法。 我们没有实验定点推理。
3. AllDifferent算法的实现
在本节中，我们将报告GAC AllDifferent传播器的一些实现细节，然后我们将其用于优化的经验评估。 这给出了对任何实施者面临的主要和一些次要问题的调查。 除了两个匹配算法之外，我们要么根据文献，要么根据似乎合理的目的来做出设计决策，而不是将我们的选择置于严格的经验评估之下。 在这一节中，我们选择了两个二分最大匹配算法进行以后的经验比较，选择一个有一个很好的时间范围和另一个在实践中工作良好的算法。
算法1显示了AllDifferent传播子器的最基本变体。 这个变体在任何方面都不是增量的。 它只需调用FindMaximumMatching和FindsccRemoveValues。
为了支持增量匹配，将删除第1行。(增量匹配实在不断移除边的过程中，若别的约束影响删除了匹配边重新寻找新的匹配过程) 我们认为这两种匹配算法都执行迭代修复，因此不需要进行任何更改来支持增量匹配。 AllDifferent的这个变体有一个状态项，从一个调用存储到下一个调用（匹配函数）。 这不是回溯的，因为有效的匹配是回溯稳定的。 当在回溯时恢复值时，有效匹配仍然有效，因为其中的值都不被移除。
AllDifferent的两个变体都调用FindMaximumMatching和FindsccRemoveValues。 下文第3.1和3.2节介绍了这两项职能。
Régin认为AllDifferent的空间复杂度为O(Rd)，因为变量值图是显式存储的[21]。 在Régin的方法中，变量值图在从域中移除值时保持，并且必须作为搜索回溯进行回溯。 在查询域开销很大的上下文中，这是合理的。 然而，在我们的实验上下文中，查询域是廉价的。 因此，在我们的实现中，我们既不显式存储变量图，也不显式存储残差图，将空间复杂度降低到O(D)。 图是在遍历时发现的。 由于大多数边对应于变量-值对，因此检查边是否存在被实现为测试域是否包含特定值。 当从一个可变顶点发现所有边时，需要在一个域上迭代。 理想情况下，求解器将提供一个域迭代器，它将在恒定的时间内找到第一个和下一个域元素。 在我们的实验中，求解器提供了域的最小值和最大值，我们用它们来约束迭代。 为了找到从值顶点到变量的所有边，需要遍历所有变量（就像我们在这里所做的那样），或者显式地存储和回溯图。
3.1. 最大二部匹配
我们考虑的第一个算法是Hopcroft-Karp算法[14]。 Hopcroft-Karp算法的运行时间为O(√rm)，其中m为变值图的边数。 然而，当使用增量匹配时，该算法只在搜索的根节点从头计算匹配； 随后，它修复丢失了k条边的匹配。 Hopcroft-Karp的成本为O(√km)[21]。 我们在C++中的实现遵循Eppstein[8]的实现。
我们实现的第二个算法是Ford-Fulkerson[6]，它用一个简单的广度优先搜索（FF-BFS）来增加路径。 它从一个不匹配的可变顶点开始，并搜索一个增广路径。 然后应用增广路径将匹配的基数增加1。 这是迭代，直到没有更多的不匹配的变量顶点，或BFS没有找到一个增加路径。
FF-BFS在很大范围的二部图上具有良好的平均行为[25]的优点，尽管该算法在时间O(rm)上运行。 修复一个丢失了k条边的匹配，代价为O（km）。
Régin[21]采用Alt、Blum、Mehlhorn和Paul2算法，该算法是Hopcroft-Karp算法的一个变体，时间界为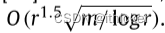
就上界而言，Hopcroft-Karp对稀疏图更好，而ABMP对稠密图更好。 我们事先不知道变量-值图的密度。
与其他匹配算法相比，我们的图相对较小。 在我们的实验中，具有最大差异约束的问题类是人为问题(r=500)。 第二大是针对社会高尔夫球手(R=480)，第三是运动日程安排(R=120)。 这并不是因为我们的例子很容易； 许多需要两个多小时才能解决。
Setubal对ABMP、FF-BFS、FF-DFS（Ford-Fulkerson与深度优先搜索）和Goldberg算法进行了实证比较[25]。 他生成了每个分区中有2p个顶点的二分图，其中p∈{8…17}。 如果我们估计我们的图在每个分区中有29个顶点，检验Setubal的结果（对每类图取最接近29个顶点的大小，并且只考虑序列计算机）表明FF-BFS对所有类都是竞争性的，并且在8/11类中是最有效的（或相等的）。
将这些结果与Setubal[24]的早期工作结合起来，我们期望FF-BFS在我们的实验中比Hopcroft-Karp有更好的表现。 情况就是这样，如第6.3节所示。
3.2. 查找SCCs并删除域值
为了计算SCCs，我们使用Tarjan算法[27]，因为它简单有效（时间范围为O(V+E)或O(Rd))。 它也适用于我们在第5节中描述的优化，其中一些信息是从算法运行中收集的。
算法1调用FindSCCsRemoveValues（算法2)，该算法查找SCCs，并移除适当的值以实现GAC。 为了避免显式存储所有SCC，这两个任务一起实现。 FindsccRemoveValues是一个简单的包装器，它初始化数据结构并调用TarjanRemoveValues，根据需要可能不止一次。 所有变量都在FindsCsRemoveValues和TarjanRemoveValues之间共享。
TarjanRemoveValues递归地执行Tarjan的算法[27]（第1-12行），并使用SCCS从域中移除值（第13-23行）。 Tarjan的算法执行深度优先搜索(DFS)。 如果它是递归实现的（正如这里所示），那么可以在递归展开时构造SCCs。 Tarjan算法的关键是根属性，通过它，一个顶点被标识为SCC的根。 在第13行测试root属性。 当根被识别时，SCC从TStack数据结构中构造。(根就是一个SCC当中dfs值最小的节点)
残差图（定义2.2）由邻域函数（第6行）给出，其中邻域(V)返回顶点集{V1,V2,…}通过有向边V→Vj与V相连的。 Tarjan算法的数据结构如下所述。
- MAXDFS是一个简单的计数器，从1开始，每次发现一个新顶点（第4行）时，该计数器就会递增。
- DFSNUM用于记录发现顶点的顺序，方法是从1开始对顶点进行编号。 dfsnum在第2行的maxdfs中设置。
- visited是访问过的顶点集。 它在第5行更新。
- TStack是一个顶点堆栈，它以空开始。 每当发现一个新顶点时，它就被推到tstack上（第1行）。 当算法检测到Curnode（DFS中的当前节点）是SCC的根时，它通过弹出TStack中的所有值来构造SCC，直到Curnode（第17-20行）。
- lowlink是关键的数据结构，其特性是lowlink[C]是所有顶点的DFSNUM中的最小值，这些顶点的DFSNUM是由DFS使用的以下边所能到达的，在R中最多只有一条边。对于每个顶点C，lowlink[C]等于DFSNUM[C]，而C是一个强连通分量的根。 LowLink[c]初始化为DFSNUM[c]。 LowLink[C]的值从第9和12行的相邻顶点更新。 当LowLink[C]使用Online13时，它已达到其最终值。
邻域函数不出现在程序代码中，以避免函数调用的开销。 相反，对于以下三种情况，第6-12行重复三次：其中curnode = t,curnode∈{x1 … xr},orcurnode∈{1 …d}.。 对于Curnode=T的情况，提前计算邻居集。 如果这个集合为空，则从残差图中省略T，因为它将是一个单例SCC。 当curnode={x1…xr,1…d}时，不需要事先显式构造邻集，就可以迭代邻集。
当算法找到一个SCC的根（第13行）时，它会做一个简单的测试来确定剩余图是否被划分（第14-15行）。 如果DFS没有遍历所有可变顶点（因为有些是不可达的），或者递归没有完全展开，那么残差图必须划分为多个SCC。
如果残差图划分，算法计算当前SCC（第17-20行）。 此SCC包含变量和值，因此在所有最大匹配中，值被分配给SCC中的变量。 因此，这些值不能分配给来自Varset的不在SCC中的任何变量。 因此，使用RemoveFromDomain从所有此类变量中移除这些值。
3.3. 次要实现细节
图算法操作小的整数集，执行诸如插入和移除整数、清除集合、测试特定整数的存在以及遍历集合等操作。 一个例子是Tarjan算法中的访问顶点集。 （在实现中，每个顶点都映射到一个不同的整数。）在所有情况下，我们都知道整数的范围（它永远不会超过0.…r+d)。
我们设计了下面的数据结构来表示0…n的子集。 我们有一个整数数组V[0…n]，由set元素索引，还有一个整数C（称为certificate）。 V初始化为0，certificate初始化为1。 元素E存在于集合IFFV[E]=C中。 为了插入元素e,v[e]← c,并为删除e,v[e]← 0。 要清除该集合，请使用c← c+1。 这样，我们就可以在小的常数时间内清除集合。
当我们要求一个集合是可迭代的时，我们还维护一个值的数组，用一个表示集合大小的整数连续存储。 通过将大小设置为0并递增certificate，仍然可以在恒定时间内实现清除操作。 对于这种类型的集合，**remove操作是线性时间的，但它很少使用，只在一个地方调用。 对于分配优化的每个应用程序调用一次（**在4.2节中描述）。
匹配的M主要表示为域值的数组，由变量数索引。 当使用Hopcroft-Karp时，它也表示为变量数组，按值索引。 Hopcroft-Karp和FF-BFS都 保持匹配中的值集。 Hopcroft-Karp还维护变量集。
4. 开发强连接组件
在本节中，我们重点介绍在搜索过程中利用强连接组件的优化。 主要焦点是在文献中第一次详细描述如何利用强连接组件的独立性，我们在2.3.5节中简要描述了这一点。 在此，我们描述了SCCS独立处理的数据结构和算法。 我们还引入了我们认为是一个新的，但次要的优化，以便在分配变量时更快地处理SCCS。
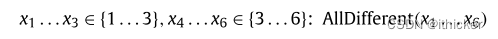
为了了解我们如何识别不相交的SCCs，请考虑（4.1）。 假设找到的匹配是xi→i对于所有i。 残差图以图表示 4.1. 在此图上运行Tarjan算法， 计算两个分别包含变量{x1…x3}和{x4…x6}的SCCs。 在对图进行分区之后，GAC算法将从变量x4…x6中剪除值3。 此时，在残差图和变量-值图中，两个SCC完全断开，并将保持如此，直到通过回溯恢复值。 在以后对传播器的调用中，可以独立地考虑这两个SCC。 这使得我们可以加快最大匹配算法和Tarjan算法的速度。 这两种算法分别在变值图的子图上运行（最大匹配算法），或在残差图的子图上运行（Tarjan算法）。 此外，当变量XI发生变化并且这些变化触发AllDifferent约束时，只需要考虑包含XI的SCC。 如下文第6.5节所示，这些变化大大提高了效率。
此方法不执行AllDifferent约束的所有可能分解。 例如，假设我们有AllDifference(x1…x6)，并且有x1…x3∈{1…4}，x4…x6∈{5…8}。 这可以分解成独立的约束AllDifference(x1…x3)和AllDifference(x4…x6)。 我们的方法不会执行此分解。 约束的两个部分都有三个变量和四个值，备用值导致X1…X3和X4…X6通过接收器T连接，因此所有六个变量都包含在一个SCC中。 尽管它不完全，但根据SCCS进行分解在实践中很有效，正如我们将在下面展示的那样。
4.1. 表示集合划分
为了存储不同算法调用之间的SCCs，需要一种可回溯的集合划分表示。 存储变量集的分区（表示为整数1…r)就足够了，因为可以从变量中快速发现值。 由于匹配算法和Tarjan算法都需要在变量集上迭代，所以分区中的每个集合都是有效的可迭代的， 这一点很重要。 迭代的顺序并不重要。 没有必要进行O(1)集隶属度测试。
当所有不同的算法执行时，它可能会进一步细分SCC，但它不会合并SCC，也不会以任何其他方式改变它们。 因此，只需要细分，在回溯时恢复集合。
对于一组整数s={1…r}，我们使用的分区表示由两个整数数组和一个回溯布尔数组组成。
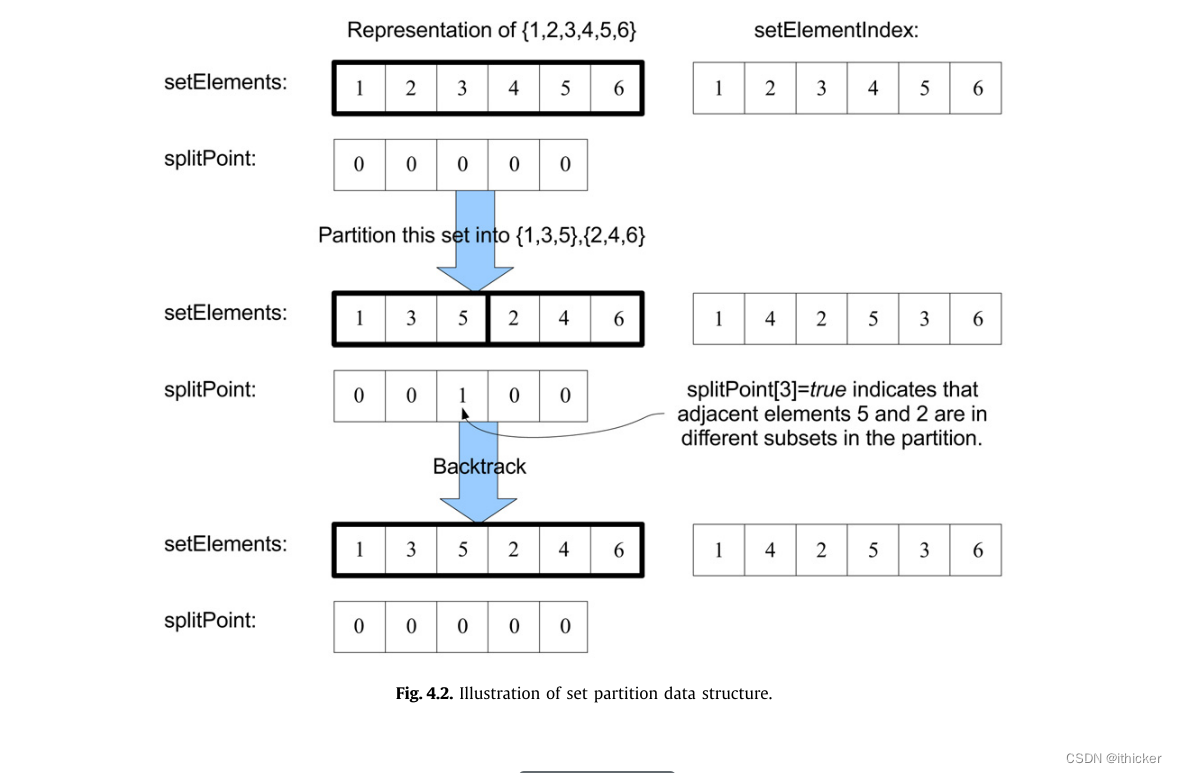
细分分区的操作包括置换setElements中的元素（并相应地更新setElementIndex）以及将SplitPoint中的布尔值从false改为true。 回溯此更改时，只需还原拆分点数组即可。 这在图得到了说明 4.2举一个简单的例子。
细分大小为n的子集需要O（N）个时间，因为可能需要在setElements数组中写入n个元素，并在setElementIndex数组中更新n个索引。 在这个操作，最多可以更改N-1个ElementSofSplitPoint，若要在回溯时撤消此操作，将还原最多N-1个SplitPoint值。 （子集分为多个集合，因为表示b和b+1元素关系，最多分为N哥集合，但是只能修改SplitPoint值到N-1）
SetElementIndex数组和SetElementIndex数组是简单的整数数组。 拆分点数组是通过尾随来维护的。 更改拆分点数组中的值的总成本为O(1)。 它涉及三个操作，每个操作花费O(1)时间：更改内存中的值，向跟踪堆栈中添加记录，以及在回溯时读取记录并恢复值。 因此，维护拆分点的成本不影响细分分区的总o(n)时间。
4.2. 分配优化
变量的分配，无论是通过搜索过程还是通过传播，都可能是一种足够常见的情况，因此优化它会有所回报。 当分配一个变量 xi 时，SCC 的计算可以稍微简化。在残差图中，xi 有一条向外的边，没有一条向内的边，因此 xi 一定在单例 SCC 中。其中 xi → a，值 a 必须从所有其他变量的域中移除。
为了优化这种情况，对包含XI的SCC s进行分区。 第一个XI与setElements中SCC的第一个元素交换。 然后将SplitPoint[setElementIndex[i]]设置为true，将S细分为S1={xi}和S2=S{xi}。 这一过程在图得到了说明 4.3. 值A从S2中所有变量的域中移除，S2被排队等待Tarjan的算法处理（因为它可能会进一步细分）。 这需要O®时间，并且不会减少对Tarjan算法的调用次数。 然而，它确实减小了Tarjan操作的图形的大小。 该优化的有效性在第6.5节中进行了测试。
4.3. 实现独立的SCCS
为了实现上述两个建议，我们用propagate-scc（算法3）代替简单的propagate函数（算法1）。 此函数需要一组名为TriggeringVars的变量作为参数。 这些变量触发了约束：在最简单的情况下，这将是自上次调用propagate-scc以来域已更改的所有变量。 当使用动态触发器（在第5节中描述）时，TriggeringVars是丢失了一个或多个触发器值的所有变量的集合。
当使用定义域计数时，TriggeringVars是定义域小于r的所有变化变量的集合。对于一个定义域较大的变量Xi，它的匹配值(m[i])可以从di中移除，而Xi∉TriggeringVars，从而使匹配无效而不触发约束。 为了涵盖这种情况，第15-17行检查SCC的匹配。 如果匹配中的某些值已被移除，则调用FindMaximumMatching。 只有在使用域计数时才需要这样做，所以我们引入了标志domaincounting，这是使用域计数的真实情况。
Propagate-SCC 遍历触发变量集，查找每个变量属于哪个 SCC（命名为 s，第 3 行）并检查匹配是否已失效（第 4 行）。如果有，则调用 FindMaximumMatching 来修复匹配（第 5-6 行）。
算法3的第7-11行实现了分配优化。 如果已分配XI，则执行第8-11行。 可能已经将s添加到ChangedSCCs，并且由于它即将被分区，因此必须将其从ChangedSCCs中删除。 这是在第8行完成的。 S被划分为单例SCC{XI}和S:S{XI}的其余部分（第9行）。 第10行执行从S2中的所有变量中移除赋值，如果需要，S2将在ChangedSCCS上排队（第11行）。 如果xi未赋值，并且s可以细分(|S|>1)，那么s被添加到changedscs（第13行）。
如果不需要分配优化，第7-13行将被替换为在ChangedSCCS中插入S的一行。
5. AllDifferent约束的动态触发器
默认情况下，对任何变量域的任何更改都会触发AllDifferent约束。 然而，有可能确定的情况下，SCCs将保持强烈连接，因此不能进行修剪。 例如，域计数，如2.3.2节所述，产生了一种这样的方法。 正如第2.3.6节所述，Katriel采取了不同的方法，将流图中的重要边定义为删除会导致进一步删除的边，并表明重要边的数量很少[16]。 然而，Katriel没有将这一观察扩展到一种方法，这种方法可以正确地实施GAC，同时（可能）减少工作。 在本节中，我们描述了一种廉价的方法，用于寻找包含所有重要边的边集，以及如何在使用动态（可移动）触发器的约束求解器中实现这一方法。
5.1. 背景
金特等人 受SAT的启发，提出了观看文字[10]。 作为触发约束传播的触发器，监视文字有三个不同于通常使用的触发器的特性。 当给定的变量-值对被删除时，被监视的文字才会引起传播； 它们的触发条件可以在搜索过程中动态改变； 并且它们在回溯时保持稳定，所以不要使用内存进行恢复。 Gent等人对元素、表和布尔和约束的观察文字已经表明是有效的。 [10、11]。
观察到的 文字传播算法通常围绕支持的概念。 对文字的支持是一个对象，它是文字一致的证据，因此不能被传播算法删除。 支持的一个例子是表约束的有效的、可接受的元组。 在这种情况下，元组可以充当它所包含的所有文字的支持。 虽然此支持是完整的，但不需要执行任何工作，但必须在支持的任何部分无效时触发约束。 支持的第二个例子是SAT中CNF子句的一对未赋值变量：这表明不能进行单元传播。 因此，它支持子句中的所有文字。
变量具有某些事件，这些事件在其域更改时发生。这些可能包括降低上限，提高下限，将变量分配给单个值或从域中删除特定值。我们指的是放置一个受监视的文字，意思是将其附加到变量事件，并清除它，从而将其从事件中删除。当变量事件发生时，求解器会遍历附加到该事件的受监视文字，并为每个事件调用相关的约束传播器。在搜索开始之前，约束会分配固定数量的监视文字。
监视文字的概念并不完全适用于AllDifferent约束，因为监视文字必须是正确的，即使它们在回溯中没有移动，这是一个称为“回溯-稳定性”的性质。 我们用作支持的对象并不总是回溯稳定的（正如我们将在下一节中演示的那样），因此必须在回溯时恢复触发器。 金特等人参考回溯观看文字作为动态触发器[10]。
5.2. 为动态触发器适应AllDifferent
当采用不同的算法使用动态触发器时，重要的结构是SCC的集合：如果每个SCC保持强连接，则不能进行传播，也不必触发约束。 因此，我们重点研究了Tarjan算法，并在残差图中识别出Tarjan算法遵循相同轨迹时必须存在的边，从而在再次执行时返回相同的结果。 在Katriel的意义上，[16]所有重要的边都必须在这个集合中。 Katriel没有给出一个显式算法来找到包含所有重要边的集合，尽管可以从她的证明中提取一个。 她的证明的构造是基于每个SCC中的深度优先搜索。 我们遵循一种非常相似的方法，但在Tarjan算法的上下文中给出了它。 该方法简单有效，只需要在Tarjan算法运行时收集一些信息。
我们收集一组T边，如下所示。 如第3.2节所述，Tarjan算法在残差图R = <V’ , E’> 中执行深度优先搜索(DFS)，DFS遍历的边E’包含在T中。每个顶点的Lowlink值也利用图中的边更新，识别SCC的判据是基于Lowlink值。 对于每一个顶点，Lowlink值可以改变多次，但在识别SCCs时只使用其最终值，因此用于获得其最终值的边包括在T中，E’中的所有其他边不包括在T中。
我们声称，去除E’中的任何边而不是T中的任何边都不影响SCCs的集合。 我们把所有这样的边放在一起考虑，因为去除边对SCCs集合的影响是单调的。 为了证明这一观点，我们证明了有向图R=<V’,T>具有与R相同的SCCs。Tarjan算法在有向图D上的执行表示为T(D)。
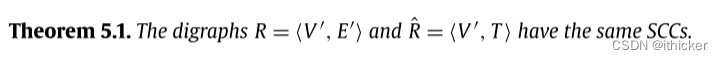
Proof. 证明了Tarjan算法对R和R返回相同的SCCs。 Tarjan的算法是正确的27。
Tarjan算法的DFS中顶点探测的顺序与结果无关。 因为顶点集是相同的，而且DFS所需的所有边根据定义都在T中，所以T®可以执行与T(R尖)完全相同的DFS。 因此，在不丧失一般性的情况下，我们假定T®可以执行与T(R尖)相同的DFS。 因此，每个顶点的DFSNUM是相同的。
在DFS树中的每个顶点V处，LowLink[V]是通过取值集Sv中的最小值来计算的。 Sv对应于V的邻域的lowlink或dfsnum，对于每个邻域，其对应值在SV中的包含仅取决于dfs序，这是不变的。 因此，所需要的就是与Sv中的最小值相对应的边在T中存在。根据定义，这就是这种情况
T®的最后一部分在递归展开时构造SCCs。 计算的SCCs取决于Lowlink的最终值和DFS的顺序。 因此T(R尖)构造了相同的SCCs集。
T中的一些边直接表示一个字面：边的形式是Xi→J或J→Xi。 我们在所有相应的文字上放置动态触发器。 忽略T中的所有其他边是安全的，因为它们不对应于域值。
图 5.1(a)在表示三个变量x1、x2、x3和五个值1、2、3、4、5的残差图上说明了这一过程。 DFS按以下顺序执行:X1，1，X2，2，X3，3，T，4，5。 DFS所穿越的八条边在图中用宽虚线表示。 最后使用三条边来改变lowlink值:2→x1、4→x2和5→x3，它们在图中用实黑表示
为了放置触发器，忽略与t之间的边。 为图 5.1(a)，触发器组为X1→1、X1→2、X2→1、X2→2、X2→4、X3→2、X3→3和X3→5。
图 5.1(b)显示了该算法在同一图上的不同执行。 在这种情况下，DFS按x1,1,t,4,x2,2,x3,3,5的顺序执行。 这给出了一组较小的触发器，因为X2→1不包括在这种情况下。 所有其他触发因素与图相同 5.1(a).
此方法每个变量最多产生3个触发器，每个备用值最多产生一个触发器（最多产生3R+(D-R)=2R+D个触发器），但并不是我们发现的所有触发器都是必要的。 例如，在图 5.1(a)，其中4→X2和5→X3上的触发器不是必需的。 其他触发器足以证明三个顶点X1，X2，X3确实在同一个SCC中。
触发器并不总是回溯稳定的。 考虑当一些边丢失时，SCC S1分成S2和S3的情况：为S2和S3计算的触发器显然没有覆盖证明S1的连通性所需的所有边，因为没有连接这两个组件的边。 因此，当在回溯时恢复S1时，触发器也必须回溯。
我们猜想，当域较大时，或者当每个搜索节点从域中删除的值很少时，这种方法会很好地工作。
5.3. 实现动态触发器的集合
这种方法实现起来非常便宜，因为它只需要从Tarjan算法的执行中收集一些信息。 不需要额外的计算。
需要对算法2进行两组更改。 首先，在算法findsccsremoveValues的顶部，清除S中变量的所有动态触发器。 然后，在当前SCC的匹配中使用的每个值上放置一个动态触发器。 这是因为这些值将在DFS期间使用。 此外，在匹配的每个值上放置一个监视文字。 这是必需的，因为匹配不是回溯的，而动态触发器是回溯的，因此当搜索回溯时，它们可能会偏离。 放置监视的文字也可以保证在违反匹配时触发AllDifferent。 在某些情况下，这将导致对同一个变量-值对触发两次约束。 然而，当将动态触发器与优先级队列结合时（第2.3.3)，当约束被触发时，它只是将触发变量添加到稍后要处理的集合中，然后返回。 因此，附加监视文字的成本是最小的。
第二组更改在算法TarjanRemoveValues中。 当curnode={1…d}时，添加与用于DFS（第11行）和用于lowlink[curnode]的最终更改（第9和12行）的边相对应的动态触发器。 如果lowlink[curnode]的最后更改发生在第12行，则一条边用于DFS和更新lowlink。 不需要放置两个动态触发器对应于一个边。 在这种情况下只放置一个动态触发器。
5.4. 内部动态触发器
完全在AllDifferent约束内模拟动态触发器是可能的。 为此，传播器将动态触发器值存储在回溯数组中。 约束将静态触发器设置为在任何域更改时触发。 当它被变量XI触发时，传播器检查触发变量的域，以查看是否丢失了任何重要的值。 如果不是，它立即返回。 对于每个变量，值都连续存储在带有长度计数器的数组中。 在我们的实验中，通过块复制来回溯数组。 我们将这种方法称为内部动态触发器。
以这种方式模拟动态触发器可能很有用，原因有两个。 首先，它可能更有效率。 将触发器值写入数组的成本非常低，清除数组（通过将大小设置为0）非常便宜。 相比之下，放置一个“真正的”动态触发器（如Gent等人[10]所描述的，用双链表实现）需要对指针进行四次赋值。 清除一组动态触发器需要对每个文字进行两次赋值。 除此之外，任何更改都必须记录在跟踪堆栈上，并在回溯时反转。 其次，求解器可能不提供动态触发器。 事实上，大多数求解器都没有提供这种功能。 因此，内部动态触发器对于所有不同类型的动态触发器的普遍适用性是非常重要的。
6. 实验评价
在这一节中，我们描述了我们的实验评估的背景。 然后我们给出了四组实验。 首先，我们在第6.3节中评估了增量匹配和优先级排队的标准方法。 其次，在第6.4节中，我们评估了动态触发器和域计数方法，这两种方法都旨在减少对传播器的调用次数。 第三，在第6.5节中，我们独立评估处理SCCS。 最后，我们将我们的最佳GAC AllDifferent约束与建立较弱一致性的传播器进行了比较。
6.1. 实验语境
对于所有实验，我们使用求解器 Minion [9,10]。我们通过以下方式调整了 Minion 0.4.1：
单调集： 我们通过一个新的接口使一个单调集对约束可用。 所谓单调，是指一旦一个集合中的一个元素在给定的节点上被移除，该元素在所有的后代节点上都保持在集合之外。 单调性允许通过尾随进行有效的实现。我们用值 true 或 false 表示每个元素：因为所有值只从 true 移动到 false，所以我们只需要存储正在更改的元素而不是将其恢复到的值。 这用于实现 4.1 节中描述的集合分区数据结构。特别是它用于 splitPoint 数组。从集合中删除一个元素及其随后的回溯恢复的成本是 O(1)。
动态触发器： 我们接受了监视文本[10]，并添加了一个跟踪机制，将它们恢复为搜索回溯。 该设施与标准监视文字共存。 在Minion中，被监视的文字可能被放置在变量-值对、上界或下界或变量上（在任何域更改时触发，或仅在赋值时触发）。监视文字也可以不使用。 AllDifferent在变量-值对上使用监视的文字和动态触发器。
Minion已经提供了我们需要的其他设施。 当约束被触发时，很容易识别触发变量。 indomain、getmin和getmax方法允许我们查询变量域。 RemoveFromDomain方法用于从变量域中移除值。
域查找在Minion中的设计是快速的，因为它是一个非常常见的操作。 这在运行图算法时很重要**，因为它们查询域以便在遍历图时发现图。 对于不同的算法，域迭代也很重要。** 不幸的是，Minion不支持域迭代，但它维护了用于绑定迭代的上下边界。
所有实验都是在苹果iMac电脑上运行的，配有2 GHz核心双处理器和2 GB内存，在OS X Tiger(10.4.11)下。 我们使用的Minion分支可以在http://minion.sourceforge.net/files/上找到，其中包括构建说明。
我们进行了广泛的测试，我们的代码已经通过。 除了在开发过程中进行持续和详细的测试之外，我们还检查了对于每个实例的每个算法变体所探索的搜索节点的数量是相同的(都是以tarjian算法为主体，所有dfs的节点数量是相同的)，只有超过时间或节点限制的实例除外。
在所有比较GAC变体的实验中，我们将搜索节点限制在500,000个，时间限制在1200秒。 由于超时的可能性，我们对速度的主要度量是每秒搜索的节点，而不是原始运行时。 对于一些社交高尔夫球手和Golomb实例，Minion直到时间限制很长之后才停止，因为时间限制执行中的一个小缺陷。
最后，我们报告的所有运行时间都是用于解决每个给定实例或超时的总时间和节点，包括所有初始化和搜索时间，包括 AllDifferent 传播器之外的时间。 这自动意味着**每个优化的所有附带特征都被考虑在内，例如额外或减少的内存使用及其对实际运行时间的影响。**然而，这确实意味着我们报告的结果通常不如我们仅在 AllDifferent 传播器内部测量运行时所获得的结果那么引人注目。尽管如此，我们经常会看到运行时有数量级的改进。
6.1.1. Minion队列机制和触发器
Minion是一个以变量为中心的求解器，具有额外的以约束为中心的队列。 概念上有两个队列，如下所述。 由于效率的原因，求解器有两个队列：变量队列非常快，因为向队列中添加变量事件是一个O(1)操作。 但是，变量队列不允许将约束赋予低优先级。 使用附加约束队列可以克服这一限制。
变量队列可以包含绑定事件的副本。 其他事件不能在队列中重复，因为它们不能在单个搜索节点上发生两次。 每个变量事件都有两个与其相关联的列表：一个是在搜索开始前固定的静态触发器列表，另一个是双链的动态触发器列表。 若要传播变量事件，求解器将遍历两个列表，调用与触发器关联的传播器。 每个触发器都包含一个传递给传播器的整数。 通过这种方式，传播器可以识别是哪个触发器（因此是哪个变量事件）触发了它。
约束队列
约束队列包含指向约束的指针。 约束负责设置触发器，并根据需要将自身添加到约束队列中。 这样，当变量队列触发约束时，它可能会执行一个测试，以确定是否应该将记录添加到约束队列中。 这使我们能够实现域计数（如2.3.2节所述）和内部动态触发器（如5.4节所述）。
实际上**，当从变量队列触发时，约束可能会失败，更新内部数据结构并执行传播**，因此这种机制比Lagerkvist和Schulte的Advisors（第2.3.7节）更通用，后者不允许执行传播。
约束队列允许重复，但是AllDifferent约束保留了它是否存在于约束队列中的记录，从而避免了重复。
约束队列不是优先级队列。 但是，约束队列的优先级低于变量队列：在从约束队列中处理每个项之前，变量队列被清空。 在下面的所有实验中，使用约束队列的唯一约束是AllDifferent约束，因此它的优先级低于任何其他约束。
处理队列的整体算法如下所示。
6.1.2. 成对无差别
Minion提供了一个简单的AllDifferent传播器，每当变量被赋值时就会触发该传播器，并从所有其他变量的域中移除赋值。 这显然是一个非常简单和快速的算法。 它在二进制不相等约束的团上执行与AC相同的传播，因此不能实现GAC。 我们称之为成对传播器。
6.1.3. 阶段性差异
如第2.3.4节所述，Schulte和Stuckey提出将廉价繁殖体（类似于上述两两繁殖体）与GAC AllDifference结合[22]。 他们提出了两种方法来实现这一点：简单地发布两个约束，或者从两个传播器构建一个分阶段传播器。 他们在他们的实例上显示了在Gecode中分阶段传播的效率更高[22]。
所提出的分段传播器利用了Gecode的多个约束队列，在Minion中不可能精确实现。 我们实现了一个近似的模拟。 无论何时从变量队列调用分段传播器，它都会检查是否分配了触发变量。 如果是，则从所有其他变量的域中移除赋值。 除了这个额外的检查之外，分阶段传播器与传统的传播器是相同的。 这个非常简单的改变产生了非常好的实验结果，如6.3节所示。
6.2. 基准集
我们生成了大量的基准实例，这些实例可以在http://minion.sourceforge.net/上获得。
Langford数问题(CSPLIB[13]中的prob024),k=2（即每个数出现两次）,n∈{10,11,12,…,25}。 这是用一个长度为2n的矢量V建模的，这是完全不同的，其中元素V[i]和V[i+n]表示色i在问题中的两个位置。 该模型由Gent、Miguel和Rendl[12]提出。 变量顺序跟随向量v的索引，值顺序是上升的。
Golomb标尺问题（CSPLIB中的prob006）是构造一组n个整数，这些整数都是不同的，并且对之间的间隔都是不同的。 假设最低的整数为0，最高的整数使用分支和定界来最小化。 它被建模为一个整数对之间的n(n-1)/2差的向量，向量上有一个单独的AllDifferent约束。 变量顺序跟随向量的索引，值顺序是上升的。
平衡含孔拟群(QWH)[17]是一个具有特定结构的部分拉丁方的完备问题。 实例是从n阶的随机完全拉丁方{20,25,30,35}中生成的。 每个尺寸产生10个拉丁方块，打1.7×N^1.55个孔来产生平衡的部分拉丁方块。 孔的数量产生在困难峰值或接近困难峰值的实例。 该问题被建模为一个n×n的变量矩阵，域为{1…n}，每行和每列都有不同的约束。 变量顺序沿行从左到右。 在矩阵中按顺序搜索这些行。 值顺序是升序。
Social Golfers（CSPLIB中的prob010)是将GS的高尔夫球手分配到S组的问题，每个W周，这样两个高尔夫球手永远不会在一起玩超过一次。 它被建模为变量的W向量，域为1.…g×s，表示周数。 对于每个星期，向量被划分为S集。 为了打破一些对称性，盘在周内按lexordered排列，高尔夫球手在盘内按lexordered排列，周按lexordered排列。 每个星期向量都有一个不同的约束。 域为{1…gs(gs-1)/2}的变量的第二个向量表示一起玩的对。 对于每个星期，对于同一集合中的每对变量，使用表约束将这两个变量映射到对向量中的单个变量。 对向量有一个完全不同的约束。 我们生成了G=4的Social Golfers实例和以下其他参数w，s:5，4…86，4…8，7，5…8，8，6…8，9，7…8，10，8，总共生成了20个实例。 变量顺序是每周依次搜索，对于每一周，我们遵循W向量的索引。 值顺序是升序。
运动计划类似于G=2的社交高尔夫球手（即比赛涉及两个队）。 n支球队在n-1周内进行n/2场比赛。 每队在每个球场上最多打两次。 它被建模为n-1个变量向量，域为1.…n表示周数。 向量被划分成对。 为了打破一些对称性，每一对都是有序的，周是lex有序的。 此外，球场是可互换的，所以每个球场上的游戏向量都是按规则排列的。 运动调度还具有AllDifferent的对向量，以及两种表示形式之间的表约束。 这样就保证了每支球队和其他球队比赛一次。 变量和值的顺序与社会高尔夫球手相同。
设计问题是为了显示动态触发器和域计数的好处。 这是病态的，因为GAC AllDifferent约束不执行剪枝，尽管执行了大量的计算。 它由两个向量V和W组成。 V的长度为5，变量的定义域为{1…50}。 一个AllDifferent约束（使用PairWisePropagator）被放置在V，并且V[4]=V[5]。 因此没有解决办法。 两两AllDifference的存在只是使问题不能满足，同时引起了研究人员的广泛搜索：二叉搜索树有50×49×48×47=5527200个左分支。 W是一个长度为L≥4的向量，包含区域为{1…D}的变量，在W上施加不同的约束，两个向量V，W由V[1]≠W[1]，V[2]≠W[2]，V[3]≠W[3]，V[4]=W[4]连接。 因此，每当赋值V中的变量时，就会通过传播从W中的变量中移除一个值。 变量顺序跟随V的索引，值顺序是上升的。
我们生成了具有L={100,200,300,400,500}的实例，其中D=L或D=L+1两种类型。 这两种类型都可以很好地使用动态触发器，因为每个左分支只删除一个值，这不太可能触发GAC。 使用域计数时，当d=l时，约束总是通过移除单个值来触发。 然而，当d=L+1时，约束永远不会触发，因此传播器只在根节点执行。 在这种情况下，域计数应该优于动态触发器。
6.3. 实验一：文献中提出的变体
优先级排队和增量匹配是标准技术。 在这个实验中，我们测试它们的优点。 我们还考虑了一种可供选择的匹配算法和分阶段传播。
Simple： AllDifferent的最简单变体如算法1所示。 它不使用约束队列，因此为每个变量事件调用一次。 Simple不独立处理SCC，也不使用动态触发器或域计数。 采用Hopcroft-Karp算法进行匹配计算。
PriorityQ： 简单算法，但从约束队列调用。 它被添加到任何变量事件的约束队列中，除非它已经存在。 因此，重复项被移除，约束在所有其他约束之后传播。
priorityq-incmatch：使用增量匹配的priorityq。 （删除了第1行的算法1，这样从一个调用到下一个调用都保留匹配。）
PriorityQ-incmatch-bfs：这是使用FF-BFS匹配算法而不是Hopcroft-Karp的PriorityQ-incmatch。
priorityq-incmatch-bfs-stagement： 这是priorityq-incmatch-bfs具有stagement传播，如第6.1.3节所述。
首先，在我们的基准集上对Simple和PriorityQ进行了比较。 我们希望PriorityQ在所有实例中都能表现得更好。 图 6.1表明情况并非如此，尽管大多数实例都受益于约束队列，有些实例的性能要好100倍以上。 这主要与Schulte和Stuckey[22]关于优先级排队的结果一致，尽管他们的结果不那么引人注目。
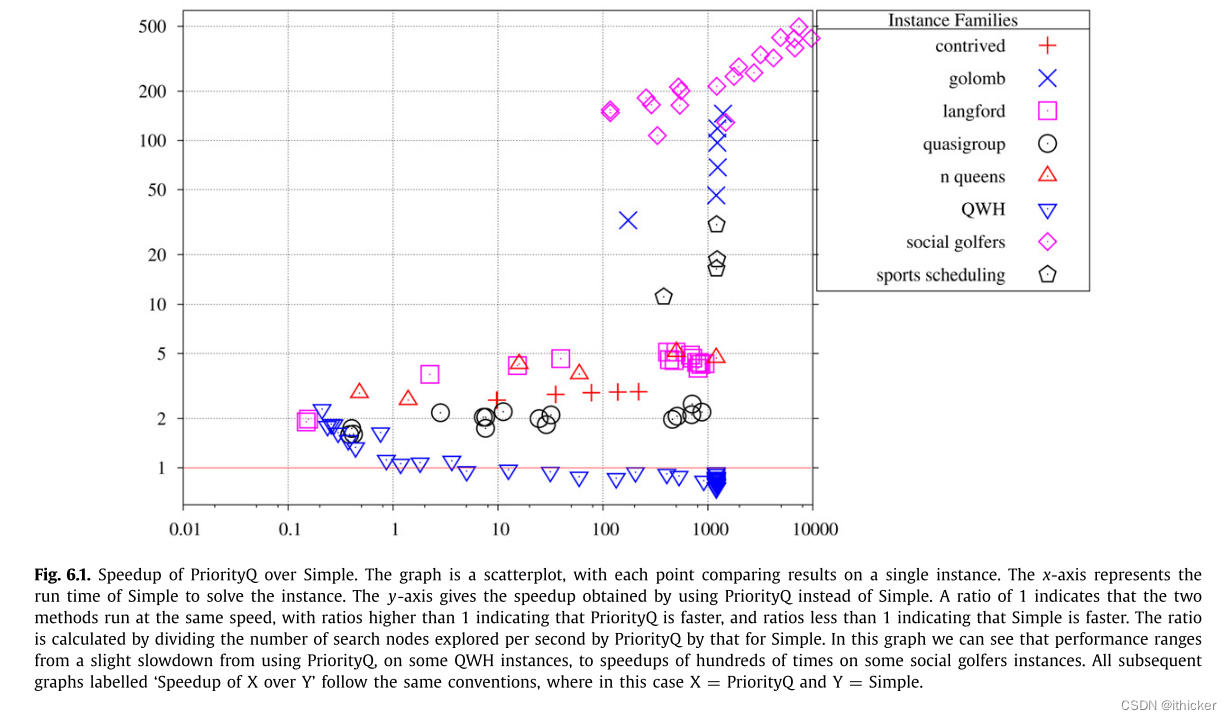
在所有进一步的实验中，我们同时使用约束队列和增量匹配，因为它们是标准技术，并且在此上下文中被验证是有用的。 我们在所有进一步的实验中都使用FF-BFS算法，因为它通常比Hopcroft-Karp更快，从来没有比它更慢。 我们还使用分阶段传播，因为它的平均速度要快得多。 将PriorityQ-IncMatch-BFS-Staged与Simple相比，我们观察到了2.14～863倍的加速比，除去人为的实例族，平均加速比为80.8。
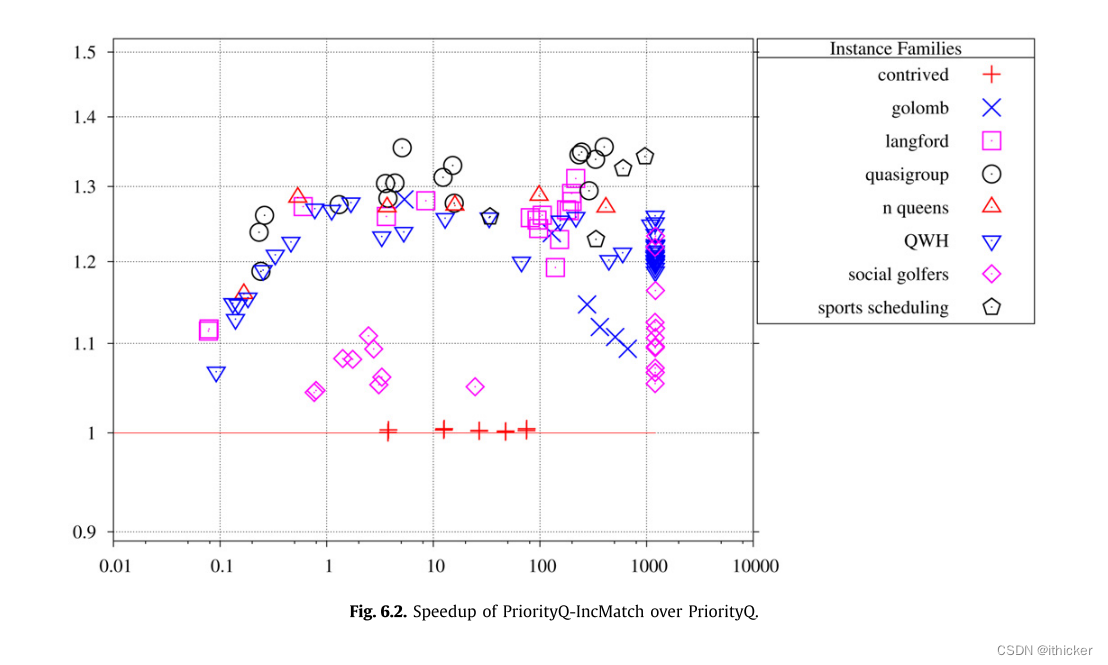
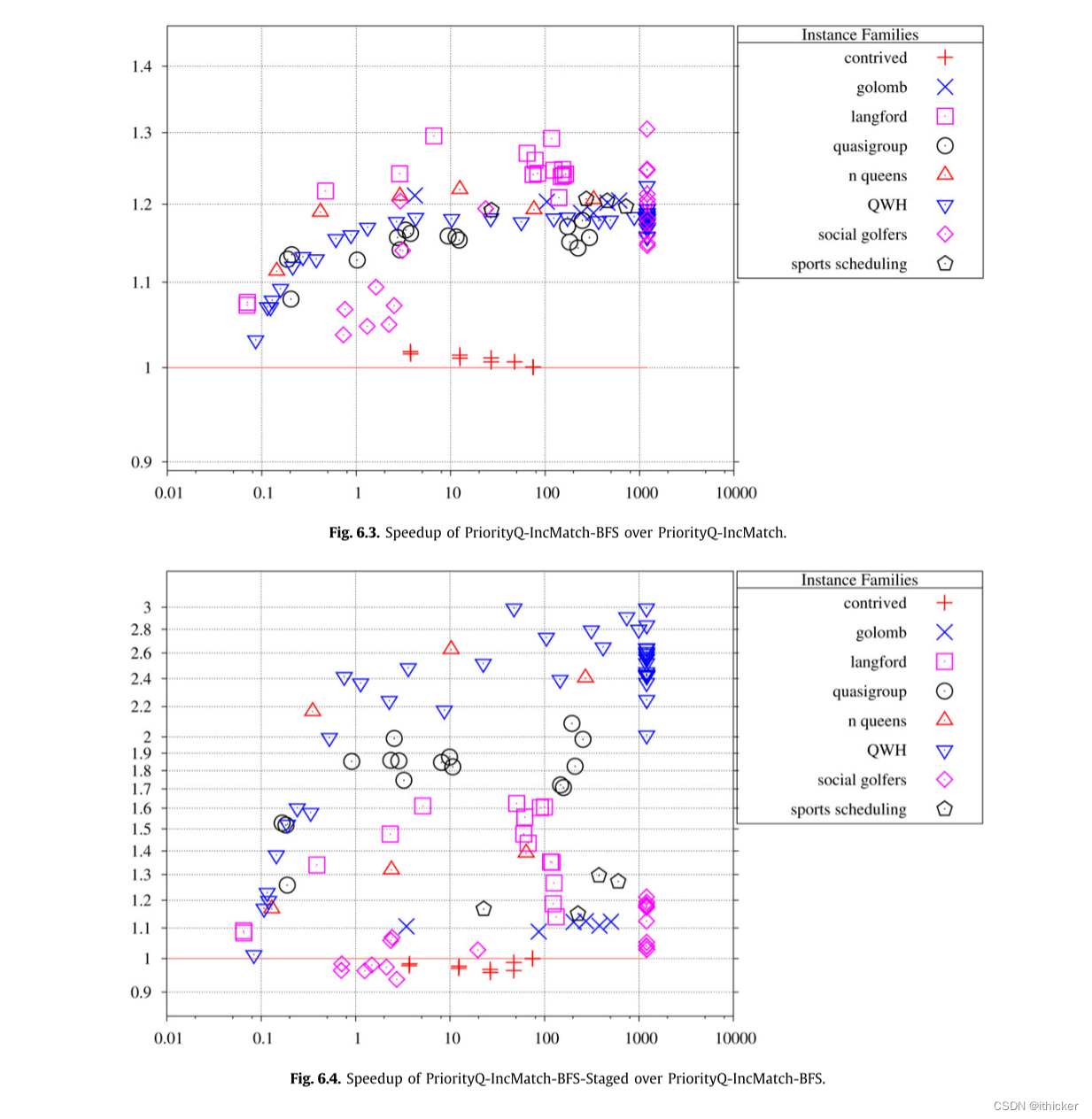
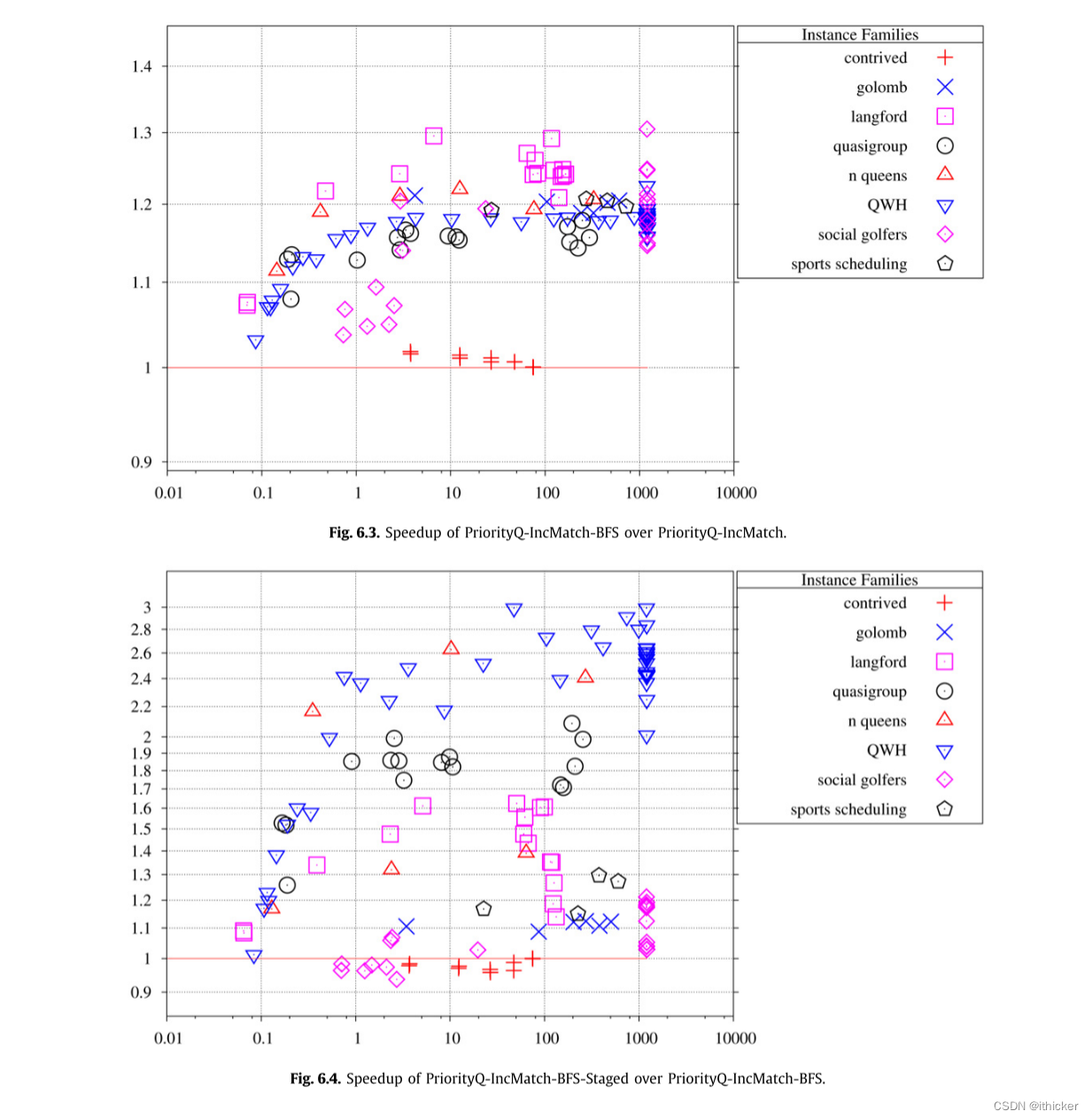
6.4. 实验二：动态触发器和域计数
为了本实验的目的，所有变体都将使用约束队列和增量匹配。 目的是比较唤醒所有域事件与使用动态触发器和域计数。
基线：与上一节中的priorityq-incmatch-bfs-stagement相同。
DynamicTrigger：增加动态触发器的基线，如第5节所述。
DynamicTriggerInternal：添加内部动态触发器的基线（第5.4节）。
DomainCount：当约束是从变量队列触发的，而约束队列中不存在约束时，将计算触发变量的域DI。 （默认情况下，在Minion中不维护值的数量。）如果di<r，则将约束添加到约束队列中。
图 6.5显示DynamicTrigger和Baseline之间每秒搜索节点的比率。 实例分散在1的上方和下方，这表明DynamicTrigger的优势在许多情况下被其开销所抵消。 正如预期的那样，使用DynamicTrigger所有设计的实例都要快得多。 图 6.6显示了DynamicTriggerInternal和Baseline之间的相同图。 DynamicTriggerInternal在大多数实例上的性能略好于Baseline，每秒探测的节点数是Baseline的1.3倍，平均提高了6%（不包括做作的）。 令人惊讶的是，人为的实例是一个例外，因为它们使用DynamicTriggerInternal比使用Baseline慢。 在DynamicTriggerInternal中，放置动态触发器的成本要低得多（因为它们只是被写入数组）。 但是，数组通过块复制进行回溯，对于设计的实例，数组很大。
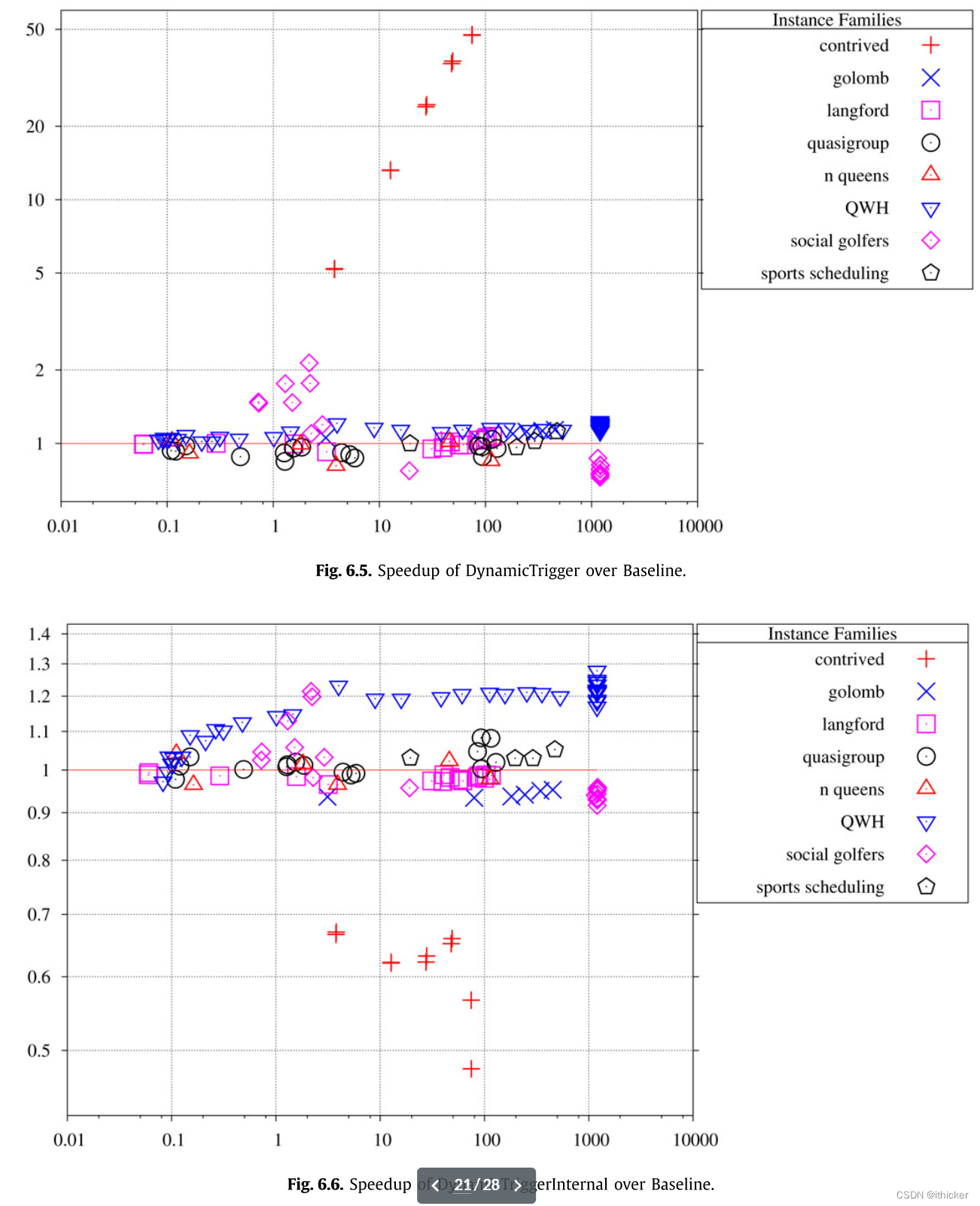
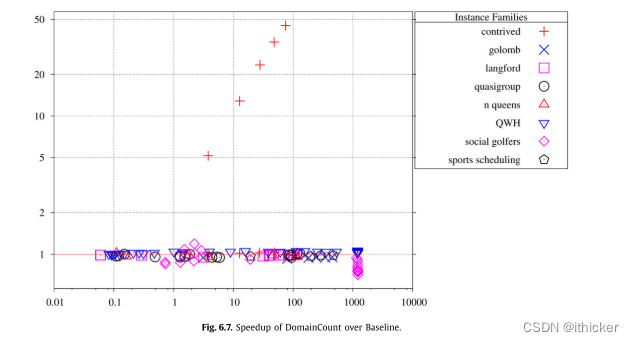
最后，我们比较了domaincount和baseline。 每秒搜索节点的比率如图所示 6.7. 域计数是便宜的，所以没有实例明显慢，但它也从来没有实质性的胜利。 这也许并不奇怪，因为域计数最初是用于具有非常大域的集合或元组变量[20]。 设计的实例与预期的一样，其中d=r+1的实例显示了域计数的巨大优势，而d=r的实例显示了不优势。
我们对这个实验的结论是，内部动态触发器平均来说是值得的，而动态触发器的开销太大， 域计数在这个基准集上不能很好地工作。
6.5. 实验三：独立处理SCCs
第4节中描述的SCC优化旨在减少运行图算法所花费的时间。 它与域计数无关。 然而，动态触发器和SCC优化之间存在依赖关系，因为在较小的图上运行Tarjan算法可能会导致较少的触发器被移动，因此可能会减少使用动态触发器的开销。 对于这些实验，我们忽略域计数，但考虑动态触发器。
**基线：**与实验一的priorityq-incmatch-bfs-stagement相同。
SCC：除基线外，SCCS还按照第4节的描述进行独立处理。
**SCC-AssignOpt：**除了SCC之外，还使用了第4.2节中描述的分配优化。
**SCC-AssignOpt-DynamicTrigger：**除了SCC-AssignOpt，还使用了动态触发器。
SCC-AssignOpt-DynamicTriggerInternal：除了SCC-AssignOpt，还使用内部动态触发器。
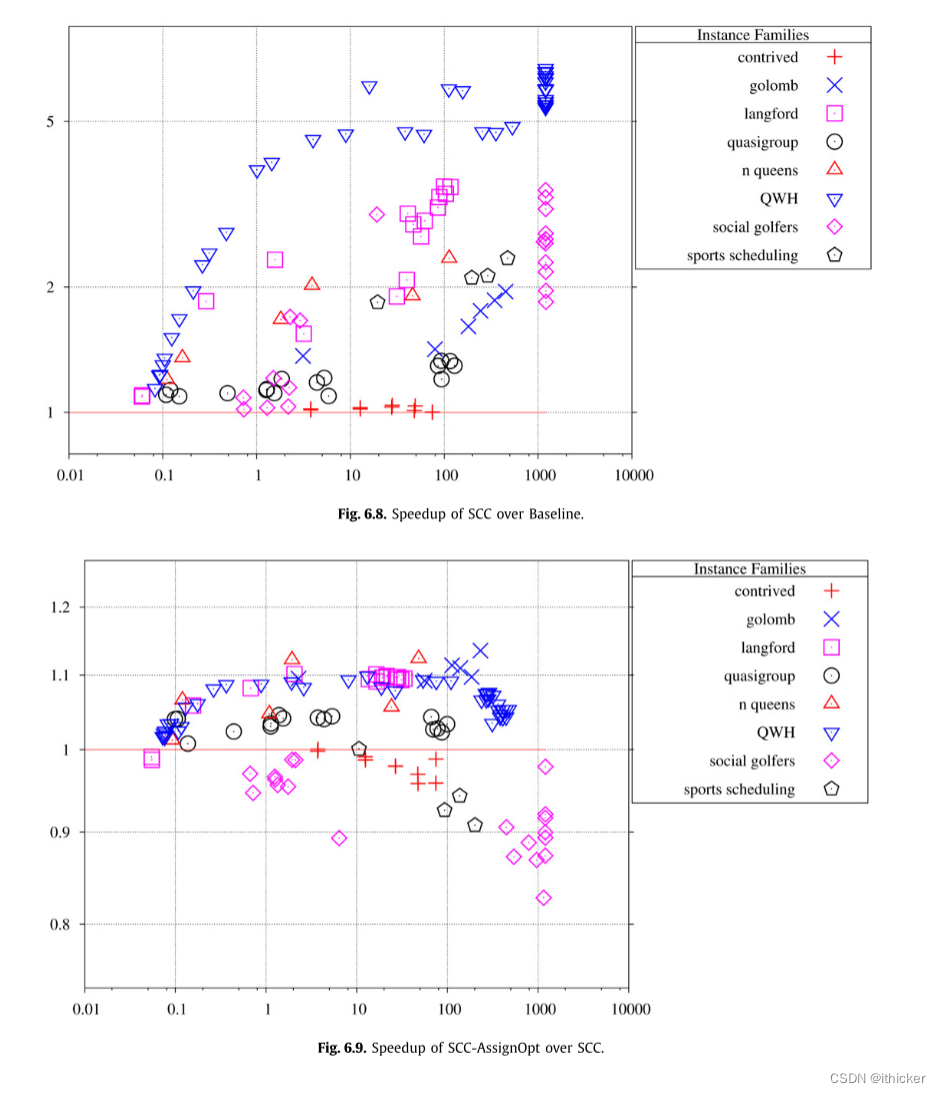
图 6.8显示了SCC与基线的比较结果。 SCC变体能够在基准测试上每秒搜索多达10倍的搜索节点，并且SCC永远不会比基准测试慢。 这是预期的，因为SCC没有太多的额外成本，并且在较小的图上运行图算法的潜在节省是很大的。
将SCC-AssignOpt与SCC(Charles 6.9）进行比较，表明AssignOpt在节点/秒上的平均改进仅为3%，但不包括人为的实例。
社交高尔夫球手和运动日程安排问题用AssignOpt解决得更慢。 这两个问题具有相似的结构，但对向量有很大的不同约束。 这可能表明AssignOpt不能很好地扩展到大型约束。
在分阶段约束中，在分配优化中所做的部分工作（从SCC中的其他变量中移除分配的值）是多余的，可以移除。 这可以稍微改善AssignOpt。
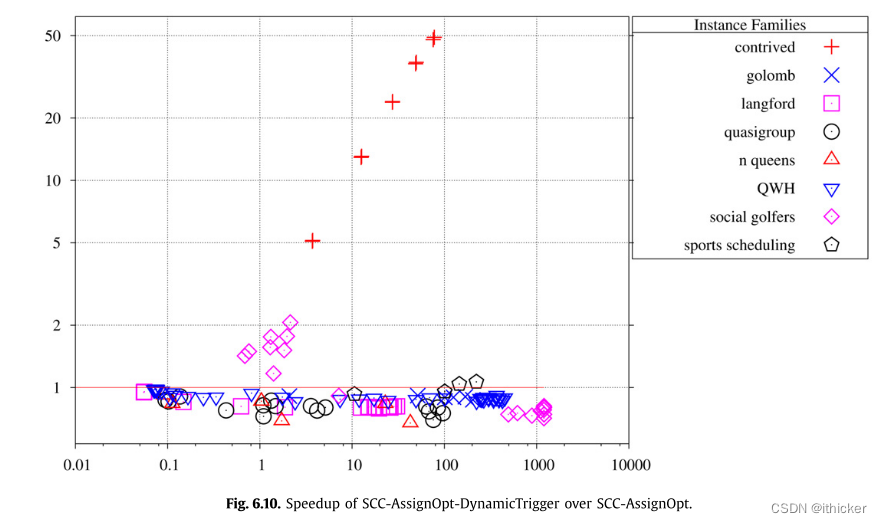
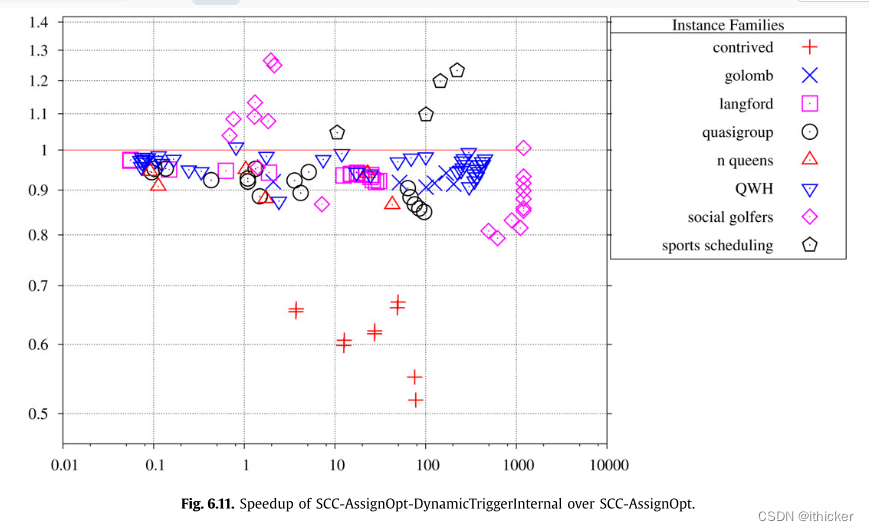
图 6.10显示了SCC-AssignOpt-DynamicTrigger与SCC-AssignOpt的比较结果。 除了几个社交高尔夫球手的例子，这些结果对动态触发器来说并不乐观。 使用动态触发器，许多实例的解决速度要慢得多。 内部动态触发器（图6.11）更好，可能是因为移动触发器的成本更低。 使用内部动态触发器可以更快地解决体育调度实例。 然而，平均而言（排除人为的问题），内部动态触发器损失5%。 这与没有SCC和AssignOpt的实验形成鲜明对比，在实验中，内部动态触发器增加了6%。 开发SCCS和分配优化降低了应用图算法的成本，因此现在不值得应用内部动态触发器。
由于动态触发器在这种情况下做得不好，我们认为SCC-AssignOpt是我们整体上最强的变体。
6.6. 实验四：与成对传播者的比较
我们将成对传播器（在6.1.2节中描述）与最有效的GAC AllDifferent变体进行了比较。 由于这两个传播器不提供相同级别的一致性，因此比较节点速率的用处有限：它只会显示维护GAC的开销，而不会显示好处。 因此，我们比较解决方案的时间，使用长得多的7200秒时间限制和没有节点限制。 我们使用的GAC AllForeign的变体是实验三中的SCC-AssignOpt。 我们把这称为最佳，把成对传播者称为成对。
图 6.12显示了一个求解时间的图，在x轴上成对，在y轴上成对比最好。 线x=7200上的点表示成对超时的实例。 GAC有两个实例超时，而不是成对超时，这是在x>1000和y<1的区域。
显然，在某些情况下，基于AllDifferent约束的GAC推理是非常重要的。 特别是，QWH和一些困难的社会高尔夫球手实例用GAC解决得更快。 在某些情况下，它们比成对解决的速度快1000倍以上。 许多作者（例如Stergiou和Walsh[26])发现GAC AllDifference很重要。
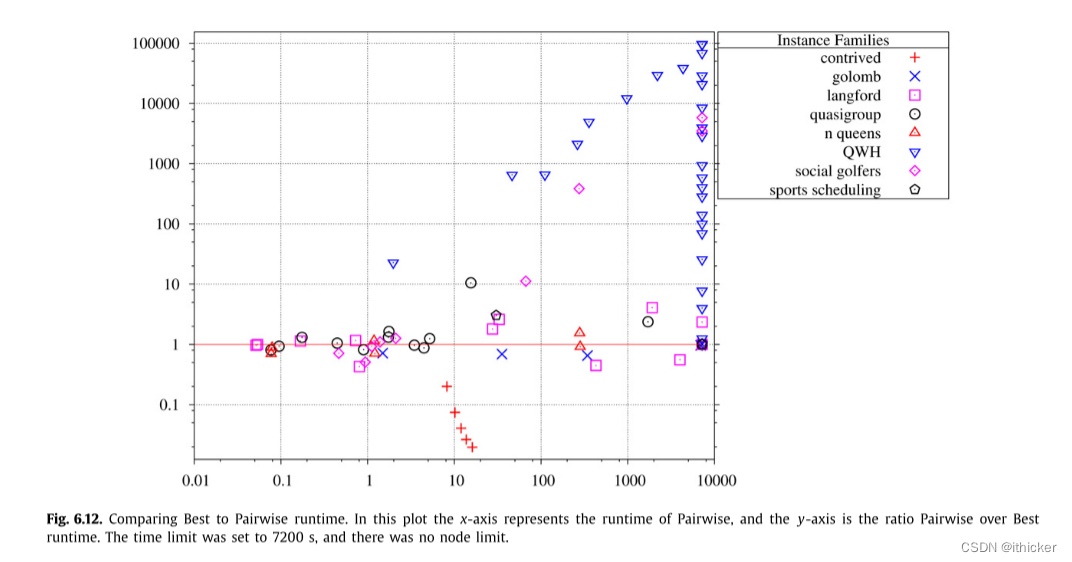
有**大量的实例导致GAC和Pairwise都超出了时间。**有两种情况是GAC超时并成对完成 (Golomb标尺n = 13，Langford的n = 14)，但是有22种情况是成对超时并GAC完成，尽管其中许多属于QWH类。**对于许多其他情况，GAC的性能不如成对。**但是，忽略人为设计的实例，成对的速度永远不会比GAC快2.34倍。有趣的是，这适用于容易和困难的情况，而不会随着情况变得更加困难而增加分歧。
总体而言，本实验表明，添加GAC AllDifferent传播器极大地扩展了Minion解决具有挑战性问题实例的能力。
6.7. 实验结论
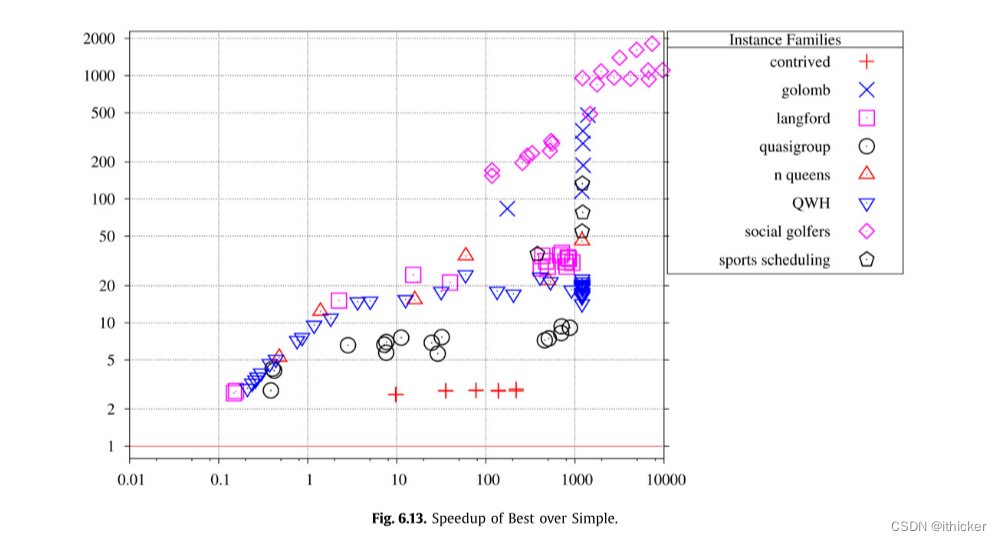
我们分别评估了GAC AllDifferent算法的许多不同的效率度量。 在本节中，我们一起考虑它们的影响。 图 6.13与Simple相比效果最好。 包括设计的实例，我们得到了从2.69倍到1813倍的加速，平均168倍。 显然，Best是对Simple的一个巨大改进，这表明了很好地实现AllDifferent的重要性。
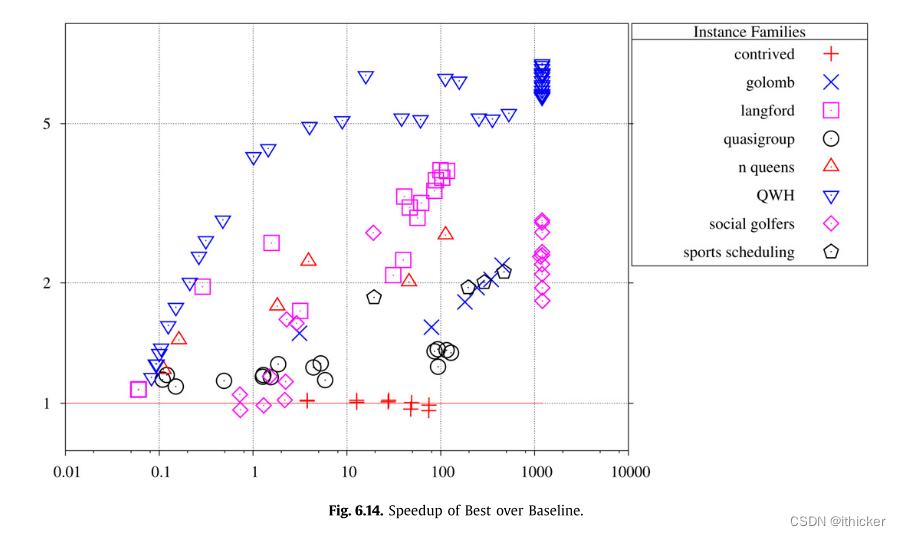
Simple不包括标准优化（优先级排队、增量匹配或分段），它使用Hopcroft-Karp而不是更高效的FF-BFS来执行匹配。 因此在图 6.14我们与基线进行了最好的比较。 这两种算法之间的唯一区别是优化，我们已经在第4节中描述了如何利用SCCS。 除了病理性的人为实例外，其他的都快了0.96～7.06倍，平均提高了2.98倍。6由于这些图是用于求解实例的，所以在所有不同的约束条件下的提高都要大于这一点。
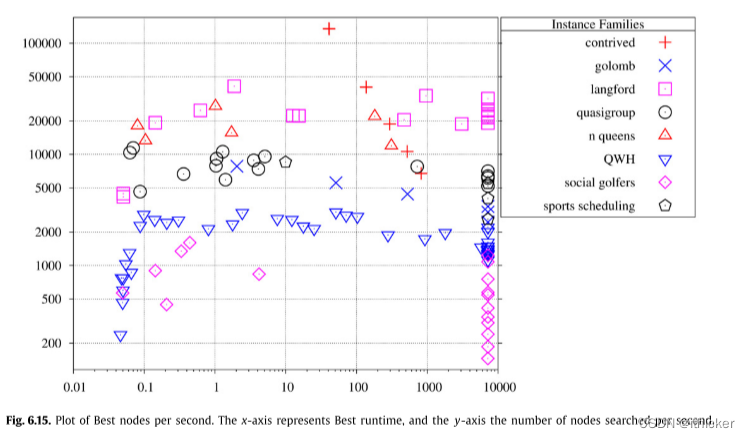
最后，图 6.15是Best每秒浏览的节点的曲线图。 这是为了给出算法在不同实例类上的速度的概念。 Langford的实例速度非常快，在某些情况下超过每秒20,000个节点，这在维护GAC时可能是非同寻常的。 Social Golfers和QWH是最慢的类，因为Social Golfers有很大的Allduffant约束（对于最大的实例，r=480，d=496)，而QWH每个实例有大量的约束（70个约束，其中r=d=35个）。
7. 实施建议
在这一节中，我们从我们的实验结果的细节中抽象出来，给跟随我们的人在实现所有不同的GAC或进一步优化它的研究提供简短的建议。
我们的结果表明，使用以下优化有巨大的好处，按重要性排序：在一个独立的队列中传播所有不同的约束； 强连接组件的增量开发； 以及使用分段组合GAC和成对传播子。 从增量匹配中有一个较小但仍然重要的20-30%的改进。 我们对这些优化的结果非常重要，它们不太可能被不同的实现选择或对不同实例的研究所逆转，并且这些优化在组合时仍然有效。 我们发现我们的分配优化是值得的，虽然在3%的影响足够小，但可以省略它，以节省程序员的时间，而不会给最终用户带来不必要的损失。
我们的一些结果取决于将使用GAC AllDifferent的上下文。 我们没有发现任何类型的动态触发器是值得的。 在我们的实验中，动态触发器在AllDifferent约束内实现时要好一些，这种方法也更易于移植。 我们并没有发现Lagerkvist和Schulte的Quimper和Walsh域计数的变体是有益的，即使我们对它有轻微的改进。 所有这些结论只有当我们忽略我们的一系列人为的实例时才适用，在这些实例上，维护GAC增加了成本而没有任何好处。 在这些情况下，动态触发器和域计数都是自己的，内部动态触发器不如内置在Minion中的触发器有效。 因此，如果使用GAC所有不同的传播器通常无效，则可以考虑使用动态触发器和域计数，以改善这种情况下的开销。 有一个问题我们还不能得出明确的结论
有一个问题，我们还不能得出明确的结论，是最佳匹配算法在GAC所有不同的传播。 我们用简单的BFS算法和复杂的Hopcroft-Karp算法进行了实验。 我们发现BFS明显更好，可以推荐它比Hopcroft-Karp。 然而，有许多其他匹配算法，很有可能另一个选择可能优于我们测试的两个算法。
正如在导言中所指出的，我们没有针对保持所有不同的边界和范围一致性的传播器进行测试。 因此，我们不能就这些技术与维持GAC相比的相对优点提出建议。 我们将很高兴看到一项研究评估这些算法的优化与本文类似的路线，以使最公平的比较与我们的优化GAC实现。
8. 结论
我们对利用Régin算法建立所有不同约束的广义弧一致性(GAC)的传播方法进行了广泛的综述。 我们调查了文献中提出的许多优化方法和一些以前没有报道过的方法。 对于这些方法中的大多数，我们都报告了它们的实施情况，并对它们的行为进行了实证分析。 我们已经特别注意结合彼此来评估优化，这（非常自然地）通常不是提出优化的论文的特征。 我们的实验很容易成为GAC算法最深入的实验分析。 基于它们，我们提供了建议，说明哪些优化是关键的，哪些不太常用。
我们将提请特别注意我们在搜索过程中处理强连接组件的结果。 我们从观察到单个强连接的组件可以独立处理，显示出显著的改进。 本文给出了该技术的首次详细报告和经验评价。 我们还通过将变量的赋值作为一种特殊情况，对维护强连接组件进行了较小的改进，我们认为这是一种新的优化。 这两种技术将搜索包含AllDifferent的实例的速度平均提高了3倍。
对于优化的最佳组合，我们发现在运行时，与谨慎但未优化的Régin算法实现相比，平均改进了160倍以上。 我们的结果证实，优化不是可选的额外内容，而是GAC AllDifferent的一个重要实现部分。 我们的结果还表明，GAC繁殖具有广泛的应用前景。 除了一些病理例子，与高度优化的成对AllDifferent传播相比，AllDifferent的GAC传播从未将搜索速度减慢2.34倍以上