傅里叶变换
欢迎关注公众号《故障诊断与python学习》
代码位置:https://github.com/HappyBoy-cmd/fault_diagnosis_signal_processing
参考资料:
书籍:机械故障诊断及典型案例解析(第2版,时献江)
前言
随机信号的时域分析只能提供有限的时域故障特征信息,若想进行信号的精密分析与诊断,需要更进一步的频谱分析 因为故障发生时往往会引起信号频率结构的变化,而且很多故障特征频率也是可以计算和预知的,通过监测该频率的幅值变换规律,就可以监控故障的发展过程。
频谱分析的理论基础是傅里叶变换,傅里叶变换包括傅里叶级数和傅里叶积分。本章主要介绍傅里叶变换的性质及典型信号的傅里叶变换,讨论离散傅里叶变换过程中产生的误差及提高频谱精度的方法。
1. 傅里叶级数
(1)基本原理
给定一个周期函数 x ( t ) = x ( t ± n T 0 ) ( n = 1 , 2 , 3 ⋯ , N ) x(t)=x\left(t \pm n T_{0}\right)(n=1,2,3 \cdots, N) x(t)=x(t±nT0)(n=1,2,3⋯,N) ,在一定条件下,可以根据如下公式展成傅里叶级数。
x ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n cos 2 π n f 0 t + b n sin 2 π n f 0 t ) x(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos 2 \pi n f_{0} t+b_{n} \sin 2 \pi n f_{0} t\right) x(t)=2a0+∑n=1∞(ancos2πnf0t+bnsin2πnf0t) (1)
式中 ——基频,Hz, f 0 = 1 / T 0 f_{0}=1 / T_{0} f0=1/T0 ;
——周期,s。
系数 { a n } \left\{a_{n}\right\} {
an}和 { b n } \left\{b_{n}\right\} {
bn}用下面的公式进行计算 ,即:
a n = 2 T ∫ 0 T 0 x ( t ) cos 2 π n f 0 t d t ( n = 1 , 2 , 3 ⋯ ) a_{n}=\frac{2}{T} \int_{0}^{T_{0}} x(t) \cos 2 \pi n f_{0} t \mathrm{~d} t \quad(n=1,2,3 \cdots) an=T2∫0T0x(t)cos2πnf0t dt(n=1,2,3⋯) (2)
b n = 2 T ∫ 0 T 0 x ( t ) sin 2 π n f 0 t d t ( n = 1 , 2 , 3 ⋯ ) b_{n}=\frac{2}{T} \int_{0}^{T_{0}} x(t) \sin 2 \pi n f_{0} t \mathrm{~d} t \quad(n=1,2,3 \cdots) bn=T2∫0T0x(t)sin2πnf0t dt(n=1,2,3⋯) (3)
a 0 2 = 1 T ∫ 0 T 0 x ( t ) d t = μ x \frac{a_{0}}{2}=\frac{1}{T} \int_{0}^{T_{0}} x(t) \mathrm{d} t=\mu_{x} 2a0=T1∫0T0x(t)dt=μx (4)
式中, μ x \mu_{x} μx是 x ( t ) x(t) x(t)的均值,称为直流分量, a n a_{n} an, b n b_{n} bn 为交流分量,也称谐波分量。
在数学上,傅里叶级数的概念是任何一个周期函数都可以用无限个三角函数去拟合。在信号处理领域的物理意义为:对任何一个周期信号都可以分解成如式 (2) ~(4) 的直流成分和无限个不能再分解的简谐信号(谐波分量)的叠加 或称任意周期信号中包括的频率成分如式(2)和式(3)所示。工程信号处理的一个主要任务就是分析和处理复杂信号中所包含的频率成分,这可以由傅里叶变换来完成
利用和差化积公式,我们可以得到更简洁的傅里叶级数表达式:
x ( t ) = A 0 + ∑ n = 1 ∞ A n sin ( 2 π n f 0 t + φ n ) x(t)=A_{0}+\sum_{n=1}^{\infty} A_{n} \sin \left(2 \pi n f_{0} t+\varphi_{n}\right) x(t)=A0+∑n=1∞Ansin(2πnf0t+φn) (5)
于是,幅值 A n A_{n} An和相位 φ n \varphi_{n} φn,可分别表示为:
A n = a n 2 + b n 2 A_{n}=\sqrt{a_{n}^{2}+b_{n}^{2}} An=an2+bn2 (6)
φ n = arctan b n a n \varphi_{n}=\arctan \frac{b_{n}}{a_{n}} φn=arctananbn(7)
式中,
a n = A n sin φ n a_{n}=A_{n} \sin \varphi_{n} an=Ansinφn
b n = A n cos φ n b_{n}=A_{n} \cos \varphi_{n} bn=Ancosφn
a 0 = A 0 a_{0}=A_{0} a0=A0。
也可以采用复数描述傅里叶级数,根据欧拉公式有:
cos θ = 1 2 ( e j θ + e − j θ ) \cos \theta=\frac{1}{2}\left(e^{j \theta}+e^{-j \theta}\right) cosθ=21(ejθ+e−jθ) (8)
sin θ = 1 2 j ( e j θ − e − j θ ) = − j 2 ( e j θ − e − j θ ) \sin \theta=\frac{1}{2 j}\left(e^{j \theta}-e^{-j \theta}\right)=-\frac{j}{2}\left(e^{j \theta}-e^{-j \theta}\right) sinθ=2j1(ejθ−e−jθ)=−2j(ejθ−e−jθ) (9)
代入式 (1) 式变为:
x ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n cos 2 π n f 0 t + b n sin 2 π n f 0 t ) = a 0 + ∑ n = 1 ∞ [ a n 2 ( e j 2 π n f 0 t + e − j 2 π n f 0 t ) + − j b n 2 ( e j 2 π n f 0 t − e − j 2 π n f 0 t ) ] = a 0 + ∑ n = 1 ∞ 1 2 ( a n − j b n ) e j 2 π n f 0 t + ∑ n = 1 ∞ 1 2 ( a n + j b n ) e − j 2 π n f 0 t \begin{aligned} x(t) & =\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos 2 \pi n f_{0} t+b_{n} \sin 2 \pi n f_{0} t\right) \\ & =a_{0}+\sum_{n=1}^{\infty}\left[\frac{a_{n}}{2}\left(e^{j 2 \pi n f_{0} t}+e^{-j 2 \pi n f_{0} t}\right)+\frac{-j b_{n}}{2}\left(e^{j 2 \pi n f_{0} t}-e^{-j 2 \pi n f_{0} t}\right)\right] \\ & =a_{0}+\sum_{n=1}^{\infty} \frac{1}{2}\left(a_{n}-j b_{n}\right) e^{j 2 \pi n f_{0} t}+\sum_{n=1}^{\infty} \frac{1}{2}\left(a_{n}+j b_{n}\right) e^{-j 2 \pi n f_{0} t} \end{aligned} x(t)=2a0+n=1∑∞(ancos2πnf0t+bnsin2πnf0t)=a0+n=1∑∞[2an(ej2πnf0t+e−j2πnf0t)+2−jbn(ej2πnf0t−e−j2πnf0t)]=a0+n=1∑∞21(an−jbn)ej2πnf0t+n=1∑∞21(an+jbn)e−j2πnf0t (10)
即: x ( t ) = ∑ − ∞ + ∞ C n e j 2 π n f 0 t x(t)=\sum_{-\infty}^{+\infty} C_{n} e^{j 2 \pi n f_{0} t} x(t)=∑−∞+∞Cnej2πnf0t (11)
式中, C 0 = a 0 C_{0}=a_{0} C0=a0 。
此时出现了负频率,这是由于用复数表示 cos x \cos x cosx, sin x \sin x sinx函数的结果。
下面求系数 C n C_{n} Cn:
C n = ( b n − j a n ) 2 = 1 2 2 T 0 [ ∫ − T 0 2 T 0 2 x ( t ) cos 2 π n f 0 t d t − j ∫ − T 0 2 T 0 2 x ( t ) sin 2 π n f 0 t d t ] = 1 T 0 ∫ − T 0 2 T 0 2 x ( t ) e − j 2 π n f 0 t d t n ≠ 0 \begin{aligned} C_{n} & =\frac{\left(b_{n}-j a_{n}\right)}{2}=\frac{1}{2} \frac{2}{T_{0}}\left[\int_{-\frac{T_{0}}{2}}^{\frac{T_{0}}{2}} x(t) \cos 2 \pi n f_{0} t \mathrm{~d} t-j \int_{-\frac{T_{0}}{2}}^{\frac{T_{0}}{2}} x(t) \sin 2 \pi n f_{0} t \mathrm{~d} t\right] \\ & =\frac{1}{T_{0}} \int_{-\frac{T_{0}}{2}}^{\frac{T_{0}}{2}} x(t) e^{-j 2 \pi n f_{0} t} \mathrm{~d} t \quad n \neq 0 \end{aligned} Cn=2(bn−jan)=21T02[∫−2T02T0x(t)cos2πnf0t dt−j∫−2T02T0x(t)sin2πnf0t dt]=T01∫−2T02T0x(t)e−j2πnf0t dtn=0 (12)
可见 , C n C_{n} Cn是一个复数量。由于 C n C_{n} Cn本身可以表示信号的幅值和相位,所以 C n C_{n} Cn称为有限区间 ( − T 0 / 2 , T 0 / 2 ) \left(-T_{0} / 2, T_{0} / 2\right) (−T0/2,T0/2)上信号 x ( t ) x(t) x(t)的离散频谱。
其中 ∣ C n ∣ = 1 2 a n 2 + b n 2 = 1 2 A n \left|C_{n}\right|=\frac{1}{2} \sqrt{a_{n}^{2}+b_{n}^{2}}=\frac{1}{2} A_{n} ∣Cn∣=21an2+bn2=21An ,称为幅值谱,为复数谱的幅值,为实谱幅值 A n A_{n} An的一半; arg ( C n ) = arctan b n a n = φ n \arg \left(C_{n}\right)=\arctan \frac{b_{n}}{a_{n}}=\varphi_{n} arg(Cn)=arctananbn=φn,称为相位谱。
(2) 周期信号傅里叶级数谱的特点
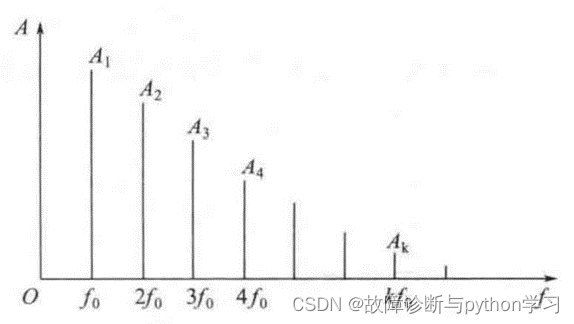
根据式 (4. 5) 可以绘出傅里叶级数的幅值谱图如图 1所示。可见,周期信号的频谱是离散的,每条谱线只出现在基波频率 f 0 f_{0} f0的整倍数上,不存在非整倍数的频率分量,随着谐波次数的增加,谐波幅值是逐渐下降的。根据这些特征,很容易在频域内判别信号是周期还是非周期的。
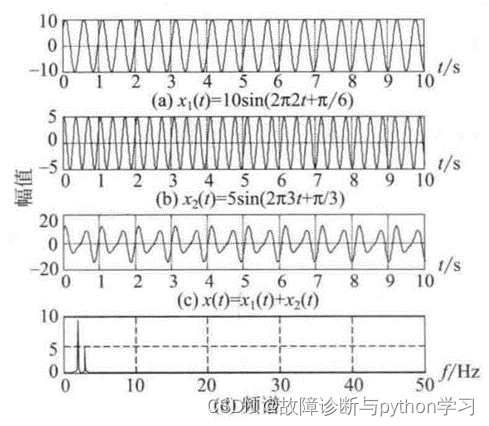
例如,例如,图 2 ( c) 中的两个周期信号的频率分别为2Hz和3,其合成显然为周期信号,且基频为 1Hz 。
图2.4 (d)为其计算频谱图,并没有图 4.1 的特征,其实,此时如果认为基频幅值为零,其仍然具有周期函数的主要频谱特征。
另外,也可对图2.5( C)中的合成信号进行频谱分析,结果如图2.5(d)所示,显然图中两个信号频率不成比例关系,虽然其时域波形很像周期信号,但是其谱特征为非周期信号(实际为准周期信号)。
(3) 典型信号的傅里叶级数谱
傅里叶级数的典型例子是方波信号[见图 3 (a) ],方波的傅里叶级数表达式为:
x ( t ) = 4 A 0 π ( sin 2 π f 0 t + 1 3 sin 6 π f 0 t + 1 5 sin 10 π f 0 t + 1 7 sin 14 π f 0 t + ⋯ ) x(t)=\frac{4 A_{0}}{\pi}\left(\sin 2 \pi f_{0} t+\frac{1}{3} \sin 6 \pi f_{0} t+\frac{1}{5} \sin 10 \pi f_{0} t+\frac{1}{7} \sin 14 \pi f_{0} t+\cdots\right) x(t)=π4A0(sin2πf0t+31sin6πf0t+51sin10πf0t+71sin14πf0t+⋯) (13)
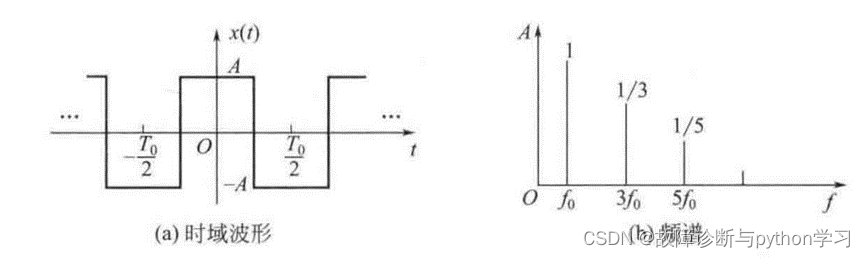
方波的频谱特点是只有奇次谐波。根据方波信号的频谱图3(b) ,也很容易判断其为周期信号。
2. 典型信号的傅里叶变换
2.1 单位脉冲信号 ( δ \delta δ函数)
(1) 函数的定义
δ ( t ) = { ∞ t = 0 0 t ≠ 0 \delta(t)=\left\{\begin{array}{ll} \infty & t=0 \\ 0 & t \neq 0 \end{array}\right. δ(t)={
∞0t=0t=0 (14)
① 函数的筛选性质
任何一函数 x ( t ) x(t) x(t)与 δ ( t ) \delta(t) δ(t)相乘的积分值等于此函数在零点的函数值 。
任一函数 x ( t ) x(t) x(t)与具有时移 t 0 t_{0} t0的单位脉冲函数 δ ( t − t 0 ) \delta\left(t-t_{0}\right) δ(t−t0)乘积的积分值是在该点上此函数的函数值 x ( t 0 ) x\left(t_{0}\right) x(t0)。
∫ − ∞ + ∞ δ ( t − t 0 ) x ( t ) d t = x ( t 0 ) \int_{-\infty}^{+\infty} \delta\left(t-t_{0}\right) x(t) \mathrm{d} t=x\left(t_{0}\right) ∫−∞+∞δ(t−t0)x(t)dt=x(t0) (15)
② 函数的卷积性质
任一函数 x ( t ) x(t) x(t)的卷积仍是此函数本身:
x ( t ) ∗ δ ( t ) = x ( t ) x(t)^{*} \delta(t)=x(t) x(t)∗δ(t)=x(t) (16)
任一函数 x ( t ) x(t) x(t)与具有时移 t 0 t_{0} t0的单位脉冲函数 δ ( t ± t 0 ) \delta\left(t \pm t_{0}\right) δ(t±t0)的卷积是时移后的该函数 :
x ( t ) ∗ δ ( t ± t 0 ) = x ( t ± t 0 ) x(t)^{*} \delta\left(t \pm t_{0}\right)=x\left(t \pm t_{0}\right) x(t)∗δ(t±t0)=x(t±t0) (17)
采用图解方法描述,如图4所示,一个在坐标原点对称的矩形函数 x ( t ) x(t) x(t)与具有时移的两个单位脉冲 δ ( t + t 0 ) \delta\left(t+t_{0}\right) δ(t+t0)和 δ ( t − t 0 ) \delta\left(t-t_{0}\right) δ(t−t0)作卷积,其结果是将 x ( t ) x(t) x(t)移至在这两个单位脉冲函数所在位置上,即任一函数与时间轴上任一点的单位脉冲函数卷积,其结果是将该函数原封不动地搬移到单位脉冲函数所在的时间轴位置。
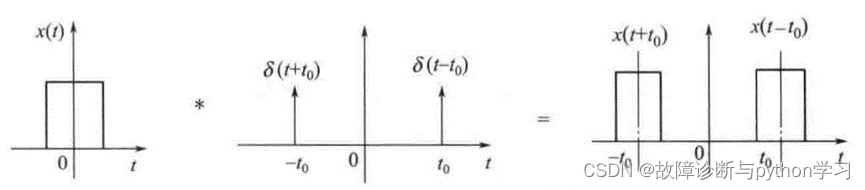
图4 任一函数与 δ \delta δ函数的卷积
(2) 函数的物理意义
δ \delta δ函数也叫冲击函数,是用以把一些抽象的不连续的物理量表示成形式上连续且能进行各种数学运算的广义函数。例如,它可以把集中载荷表示为分布载荷(分布面积为零,载荷集度为无穷大),把理想的碰撞冲量表示成一般冲量(作用的时间为零,作用力为无穷大 ),可以作为一种理想的脉冲激励函数。
采用敲击实验法测量叶片的共振频率,就是利用脉冲激励原理实现的。由锤敲击产生的冲击脉冲相当一个 δ \delta δ函数,其频谱在理论上是一根直线,也就是在所有的频段具有相同的能量,称为白噪声。在与叶片的固有频率交叉处,会产生共振,引起系统的自由衰减振动,检测这个振动频率就是被测叶片的固有频率。
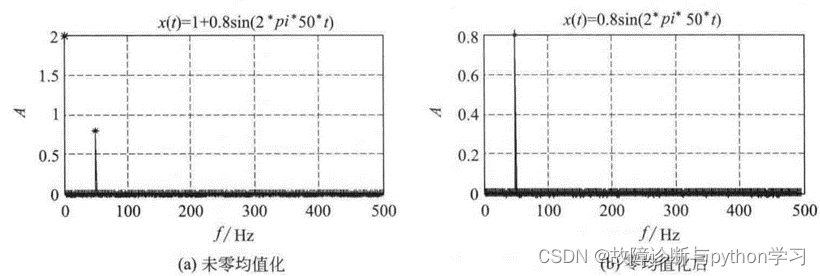
反之,直流信号的频谱是 δ \delta δ函数,所以当信号中含有直流成分时,也就是有一个均值成分存在的话,在频谱中的0频率附近就会有较高幅值的谱峰 ( 函数)出现,这会严重影响其他计算结果的显示比例,而且处于0点附近,不易被察觉,易产生误判,如图 5(a) 所示。所以,如前所述,信号处理前一般都要进行均值化处理。零均值化处理后的频谱如图 5 (b) 所示,可见,简谐信号的幅值已变为最大值,说明 δ \delta δ函数的影响被剔除。
3. 信号的采样
在信号处理领域,计算机只能处理离散的时间序列函数,因此计算机需要 把连续变化的信号变成离散信号后再进行相关的处理与运算。
3.1 采样定理
信号的采样确定了连续时间信号 x ( t ) x(t) x(t)的采样表达式 x ∗ ( t ) x^{*}(t) x∗(t),那么,采样间隔 Δ t \Delta t Δt必须符合什么样的条件时, x ∗ ( t ) x^{*}(t) x∗(t)才能保留有原连续时间信号 x ( t ) x(t) x(t)的所有信息。香农(Shannon)采样定理解决了此类问题。
设连续时间信号 x ( t ) x(t) x(t),其傅里叶换为 X ( f ) X(f) X(f), 频谱中的最高频率成分为 ,对连续时间信号 采样,采样频率为 f c f_{c} fc,采样后的离散时间信号为 x ∗ ( t ) x^{*}(t) x∗(t),如果满足条件 f s > 2 f c f_{\mathrm{s}}>2 f_{\mathrm{c}} fs>2fc,可以从离散时间信号 x ∗ ( t ) x^{*}(t) x∗(t)中恢复原连续时间信号 x ( t ) x(t) x(t),否则,会发生频率混叠,从离散信号 x ∗ ( t ) x^{*}(t) x∗(t)中无法恢复原连续时间信号 x ( t ) x(t) x(t)。
我们可以用下面的图解说明这个过程。
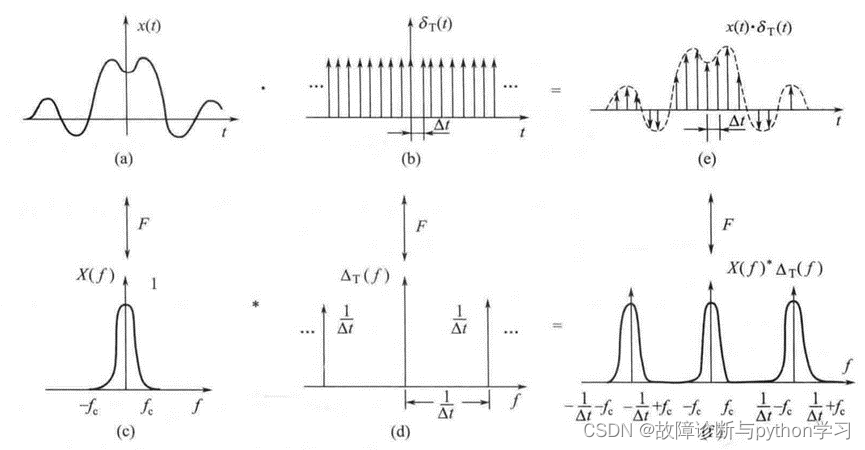
假设 x ( t ) x(t) x(t)为连续函数, δ T ( t ) \delta_{\mathrm{T}}(t) δT(t)为无穷脉冲序列,其采样间隔为 Δ t \Delta t Δt,波形如图 4.15 (a), (b) 所示 将 与 相乘即可以得到离散的 信号,其波形如图 4.15 (e) 所示,此过程称为采样,也称为时域离散, δ T ( t ) \delta_{\mathrm{T}}(t) δT(t)叫做采样函数。
可以利用卷积定理来讨论采样在频域中的变化过程。 x ( t ) x(t) x(t)和 δ T ( t ) \delta_{\mathrm{T}}(t) δT(t)的傅里叶变换分别表示于图 15 ( c) 和(d) 中。依据卷积定理,图 4. 15(f)中的图像应是图 15( c)和(d) 的频域函数 X ( f ) X(f) X(f)的卷积。由于 Δ T f \Delta_{\mathrm{T}} f ΔTf是无限个 δ \delta δ函数,所以根据 δ \delta δ函数卷积性质,只需将 X ( f ) X(f) X(f)移到每个 δ \delta δ函数位置上即可,可见离散后的信号的频谱是一个周期函数,只需观察其中的一个周期即可,它与连续函数 x ( t ) x(t) x(t)的傅里叶变换相同。
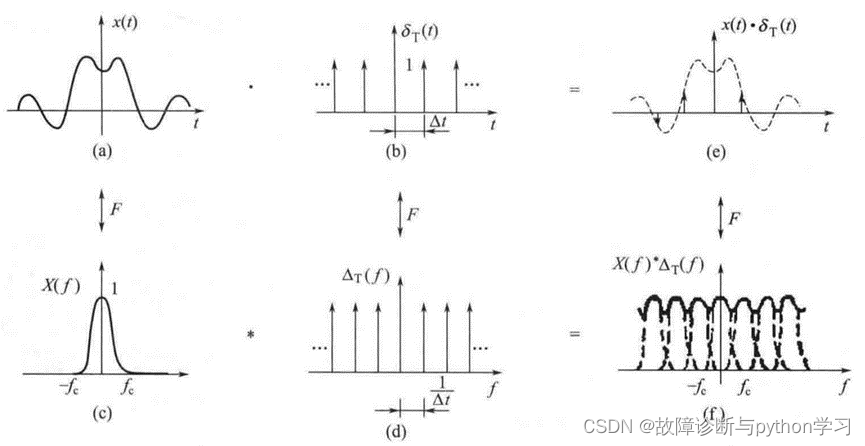
如在上例中,加大采样间隔 Δ t \Delta t Δt,其结果如图 6所示。可见由于增大了 Δ t \Delta t Δt,频域采样函数 变得更密,因为频域脉冲函数的间隔减小,它们与频谱 X ( f ) X(f) X(f)的卷积就产生了波形的相互重叠,如图 6(f)所示,函数的傅里叶变换由于采样引起的这种畸变称为混叠效应。
混叠效应产生的原因在于采样间隔 Δ t \Delta t Δt太大, 也就是采样频率过低。如何才能不产生这种现象呢?在图4.17 中可以看出,当 Δ T f \Delta_{\mathrm{T}} f ΔTf脉冲函数的频率间隔小于 2 f c 2 f_{c} 2fc,即 1 / T s < 2 f c 1 / T_{\mathrm{s}}<2 f_{\mathrm{c}} 1/Ts<2fc,卷积便出现重叠现象,这里 f c f_{\mathrm{c}} fc是连续函数 x ( t ) x(t) x(t)的最高频率成分。
如果令 f s = 1 Δ t f_{\mathrm{s}}=\frac{1}{\Delta t} fs=Δt1, f s f_{\mathrm{s}} fs称为采样频率, 不发生混叠效应的公式为:
f s = 1 Δ t ⩾ 2 f c f_{\mathrm{s}}=\frac{1}{\Delta t} \geqslant 2 f_{\mathrm{c}} fs=Δt1⩾2fc (18)
即: f s ⩾ 2 f c f_{\mathrm{s}} \geqslant 2 f_{\mathrm{c}} fs⩾2fc (19)
如果认为信号中的最高频率 f max f_{\max } fmax等于 的话, 则有:
f s ⩾ 2 f max f_{\mathrm{s}} \geqslant 2 f_{\max } fs⩾2fmax (20)
这就是香农采样定理。
实际工程中 ,取:
f s = ( 2.56 ∼ 4 ) f max f_{\mathrm{s}}=(2.56 \sim 4) f_{\max } fs=(2.56∼4)fmax (21)
对未知的信号最高频率成分 f max f_{\max } fmax,可由信号的低通滤波器的截止频率产生。
3.2 采样点数与频率分辨率
信号分析处理过程中,首先要确定的是采样频率 ,采样频率应符合采样定理。其次要确定采样点数N和频率分辨率 f s f_{\mathrm{s}} fs。采样点数受到快速傅里叶变换FFT) 变换的限制,一般情况下,只能取1024或2048 这类 2 m 2^{\mathrm{m}} 2m的点数。
采样频率 f s f_{\mathrm{s}} fs、采样点数 N N N和频率分辨率 Δ f \Delta f Δf之间的关系如下
Δ f = 1 T 0 = 1 N Δ t = f s N \Delta f=\frac{1}{T_{0}}=\frac{1}{N \Delta t}=\frac{f_{\mathrm{s}}}{N} Δf=T01=NΔt1=Nfs (22)
式中, T 0 T_{0} T0为采样总时间长度(单位为s); Δ t \Delta t Δt为采样间隔。
频率分辨率决定了频谱的分析精度,要想提高频率分辨率(降低 Δ t \Delta t Δt),应尽量减少采样频率 f s f_{\mathrm{s}} fs,或增加采样点数 N N N。
例,已知某信号的最高频率 f max = 1500 H z f_{\max }=1500 \mathrm{~Hz} fmax=1500 Hz,希望达到的频率分辨率 Δ f = 5 H z \Delta f=5 \mathrm{~Hz} Δf=5 Hz,试选择采样频率 f s f_{\mathrm{s}} fs、采样长度 T 0 T_{0} T0及采样 N N N。
采样频率 f s ⩾ 2 f max f_{\mathrm{s}} \geqslant 2 f_{\text {max }} fs⩾2fmax ,取:
f s = 2.5 f max = 2.5 × 1500 = 3750 H z f_{\mathrm{s}}=2.5 f_{\max }=2.5 \times 1500=3750 \mathrm{~Hz} fs=2.5fmax=2.5×1500=3750 Hz (23)
频率分辨率 Δ f = 1 / T 0 \Delta f=1 / T_{0} Δf=1/T0,采样时间长度 T 0 T_{0} T0为:
T 0 = 1 / Δ f = 1 / 5 = 0.2 s T_{0}=1 / \Delta f=1 / 5=0.2 \mathrm{~s} T0=1/Δf=1/5=0.2 s(24)
采样点数 N = T 0 / Δ t = T f s N=T_{0} / \Delta t=T f_{\mathrm{s}} N=T0/Δt=Tfs,于是:
N = T 0 f s = 0.2 × 3750 = 750 N=T_{0} f_{\mathrm{s}}=0.2 \times 3750=750 N=T0fs=0.2×3750=750(25)
此时, 应取 N N N应取1024,采样频率为 :
f s = N / T 0 = 1024 / 0.2 = 5120 H z f_{\mathrm{s}}=N / T_{0}=1024 / 0.2=5120 \mathrm{~Hz} fs=N/T0=1024/0.2=5120 Hz(26)
由于采样长度未变,此时,频率分辨率仍然不 变,且 f s ⩾ 2 f max f_{\mathrm{s}} \geqslant 2 f_{\max } fs⩾2fmax符合要求。
4. 离散傅里叶变换 (DFT)
离散傅变换 (Discrete Fourier Transform, DFT)是一种用计算机计算傅里叶变换的方法。
5. 快速傅里叶变换 (FFT)
其是一种高效快速计算DFT的算法
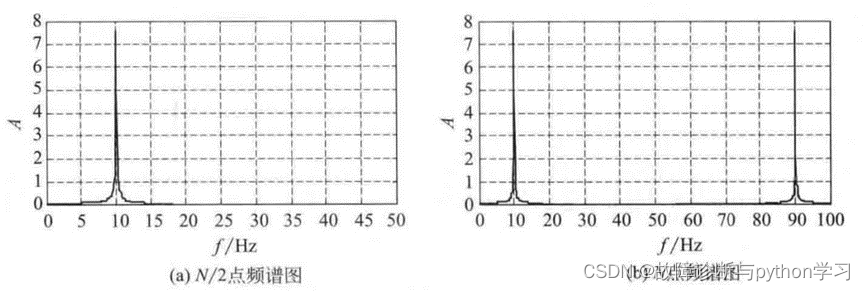
对一个时间函数 x ( t ) = 10. 0 ∗ sin ( 2 π f c t ) x(t)=10.0^{*} \sin \left(2 \pi f_{c} t\right) x(t)=10.0∗sin(2πfct)进行分析,其中信号频率 f c = 10 H z f_{\mathrm{c}}=10 \mathrm{~Hz} fc=10 Hz, 采样频率 f s = 100 H z f_{\mathrm{s}}=100 \mathrm{~Hz} fs=100 Hz,采样点数 N = 1024 N=1024 N=1024点,计算结果如图 7所示
6. FFT示例程序
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# @Time : 2022/12/17
# @Author : 李正平
# @fun : FFT示例程序
import pandas as pd
import numpy as np
from numpy.fft import fft, fftfreq
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.rcParams['axes.unicode_minus'] = False # 显示负号
font = {
'family': 'Times New Roman', 'size': '15', 'color': '0.5', 'weight': 'bold'}
6.1生成正弦曲线
fc = 10 # 信号频率
fs = 100 # 采样频率
N = 1024 # 采样点数
t = np.linspace(0, (N-1)/fs, N)
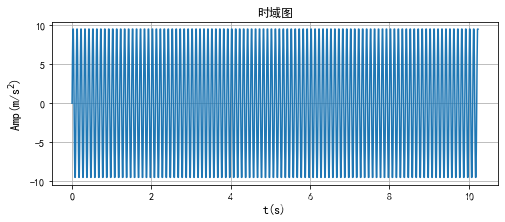
x = 10 * np.sin( 2 * np.pi * fc * t) # x=10*sin(2πft)
# 绘制时域图
plt.figure(figsize=(8,3))
plt.plot( t, x )
plt.grid()
plt.title('时域图')
plt.xlabel('t(s)', size=12)
plt.ylabel('Amp(m/s$^2$)', size=12)
plt.show()
6.2 N/2点频谱输出
先做fft
y = fft(x) # fft 计算
y # eg: array([24.89898285+0.j...]
# y.shape = (1024,)
>>>output
array([24.89898285+0.j , 24.90172703-0.09443086j,
24.90996273-0.18891404j, ..., 24.92369937+0.28350194j,
24.90996273+0.18891404j, 24.90172703+0.09443086j])
可见其fft结果为复数。我们要求幅值谱需求模:
amp_list = np.sqrt( np.abs(y) ) * 2 / N # 计算幅值谱
amp_list # eg: array([0.00974588, 0.00974645,
# shape = (1024,)
>>>output
array([0.00974588, 0.00974645, 0.00974816, ..., 0.00975103, 0.00974816,
0.00974645])
求完模后是实数。乘以2再除以N是为了还原至原始幅值。(但这里并没有还原至原始幅值大小,即10,目前还没了解是什么原因)
接下来求取横坐标,即频率序列
freq_list = np.linspace(0, ( N-1) / N * fs , N ) # 频率轴序列
freq_list # array([0.00000000e+00,...]
# shape = (512,)
>>>output
array([0.00000000e+00, 9.76562500e-02, 1.95312500e-01, ...,
9.97070312e+01, 9.98046875e+01, 9.99023438e+01])
可见其频率分辨率为fs/N,即100/1024。
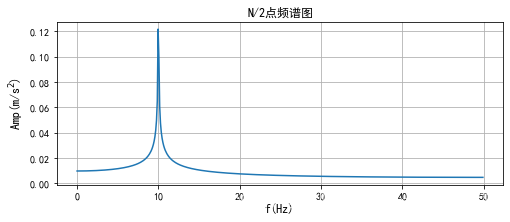
有了幅值和频率,就可以绘制频谱图了。
# N/2点频谱输出
plt.figure(figsize=(8,3))
plt.plot( freq_list[0:int(N/2)], amp_list[0:int(N/2)] )
plt.grid()
plt.title('N/2点频谱图')
plt.xlabel('f(Hz)', size=12)
plt.ylabel('Amp(m/s$^2$)', size=12)
plt.show()
6.3 N点频谱输出
# N点频谱输出
plt.figure(figsize=(8,3))
plt.plot( freq_list, amp_list )
plt.grid()
plt.title('N点频谱图')
plt.xlabel('f(Hz)', size=12)
plt.ylabel('Amp(m/s$^2$)', size=12)
plt.show()
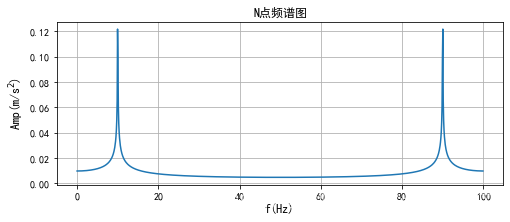
可见N点频谱与2/N点频谱图像是对称的,因此实际能观察到频率范围为采样频率的一半。
6.4 附-通过fftreq函数求频率序列
上面6.2节频率序列是自己手动生成的。fft包可以自动生成频率序列,即fftfreq()函数。
freq_list = fftfreq(n=N, d=1/fs)
freq_list
>>>output
array([ 0. , 0.09765625, 0.1953125 , ..., -0.29296875,
-0.1953125 , -0.09765625])
可知fftreq生成的频率有正频率和负频率两部分。
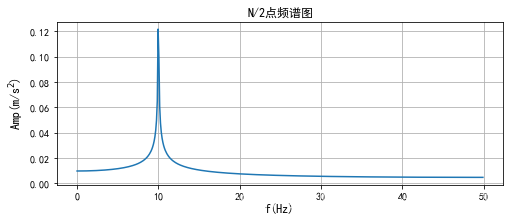
# N/2点频谱输出
plt.figure(figsize=(8,3))
plt.plot( freq_list[0:int(N/2)], amp_list[0:int(N/2)] )
plt.grid()
plt.title('N/2点频谱图')
plt.xlabel('f(Hz)', size=12)
plt.ylabel('Amp(m/s$^2$)', size=12)
plt.show()
# N点频谱输出
plt.figure(figsize=(8,3))
plt.plot( freq_list, amp_list )
plt.grid()
plt.title('N点频谱图')
plt.xlabel('f(Hz)', size=12)
plt.ylabel('Amp(m/s$^2$)', size=12)
plt.show()
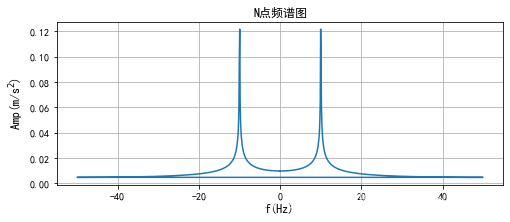
此时的频率图是关于频率为0对称。唯一的不足是应该在10Hz的幅值大小应该为10左右。目前这个地方没有摸清。图像是没问题。
6.5 定义为一个函数
def plot_fft(data_arr, fs):
"""
fun: 绘制fft图像
param data_arr: 输入数组
param fs: 采样频率
"""
N = len(data_arr)
y = fft(data_arr) # fft 计算
amp_list = np.sqrt( np.abs(y) ) * 2 / N # 计算幅值谱
freq_list = fftfreq(n=N, d=1/fs)
# N/2点频谱输出
plt.figure(figsize=(8,3))
plt.plot( freq_list[0:int(N/2)], amp_list[0:int(N/2)] )
plt.grid()
plt.title('fft频谱图')
plt.xlabel('f(Hz)', size=12)
plt.ylabel('Amp(m/s$^2$)', size=12)
plt.show()
plot_fft(data_arr=x, fs=100)
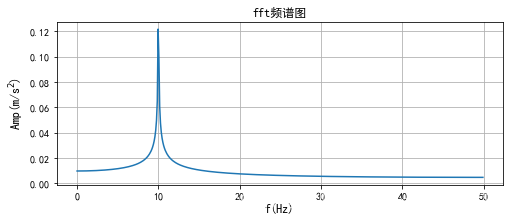
7. 总结
- 傅里叶级数的概念是任何一个周期函数都可以用无限个三角函数去拟合
- DFT是计算离散信号的傅里叶变换的一种算法
- FFT是一种高效计算DFT的算法
- 根据香农(采样)定理,采样频率应为所分析信号最大频率的2倍。实际工程应用 f s = ( 2.56 ∼ 4 ) f max f_{\mathrm{s}}=(2.56 \sim 4) f_{\max } fs=(2.56∼4)fmax。
- 采样频率为 f s f_s fs,其fft能观察的频率为 f s / 2 f_s/2 fs/2。例如采样频率为1600Hz,能观察的频率为800Hz。