文章目录
前言
近期在阅读Data-Driven Sparse Structure Selection for Deep Neural Networks论文时,用到里面APG-NAG相关优化器的知识,原论文方法采用mxnet去实现的,在这里想迁移到pytorch中。因此手撕一下APG和NAG相关的知识。
在之前文章APG(Accelerate Proximal Gradient)加速近端梯度算法 和 NAG(Nesterov accelerated gradient)优化器原理 (一)中,详细描述了APG算法,本文将简略讲一下NAG优化器,并着重讲一下Data-Driven Sparse Structure Selection for Deep Neural Networks论文中APG-NAG优化器的实现。
NAG优化器
NAG优化器主要可参考1和2两个引用。讲解的非常细致,在这里引用2中的话,并再用三张图简单描述一下:
Momentum是基于动量原理的,就是每次更新参数时,梯度的方向都会和上一次迭代的方向有关,当一个球向山下滚的时候,它会越滚越快,能够加快收敛,但是这样也会存在一个问题,每次梯度都是本次和上次之和,如果是同向,那么将导致梯度很大,当到达谷底的时候很容易动量过大导致小球冲过谷底,跳过当前局部最优位置。
我们希望有一个更智能的球,一个知道它要去哪里的球,这样它知道在山坡再次向上倾斜之前减速。
Nesterov accelerated gradient是一种使动量项具有这种预见性的方法 ----参考2
1.Momentum 更新
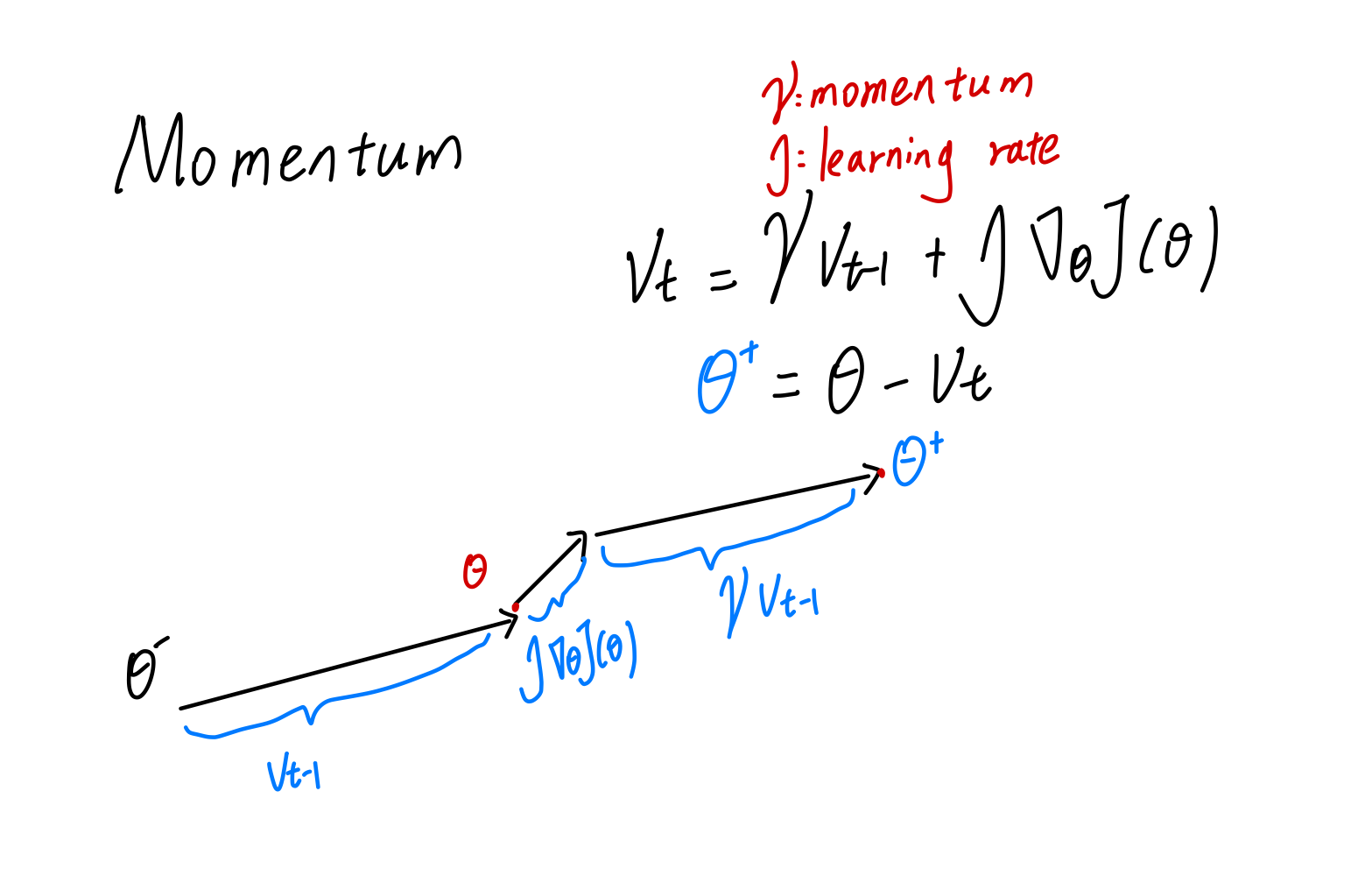
2. NAG 更新
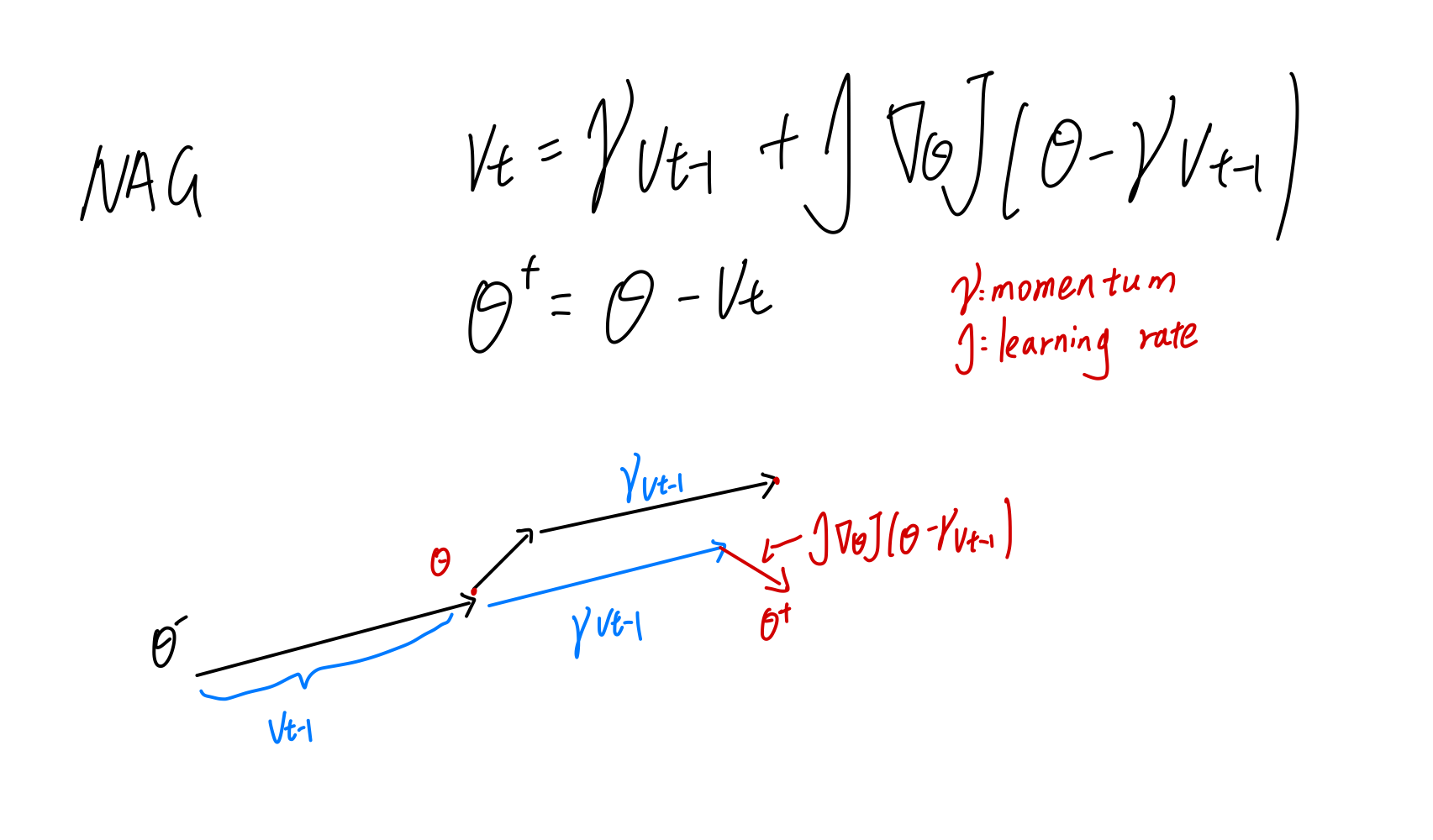
- 两者对比(蓝色为动量,绿色为NAG)
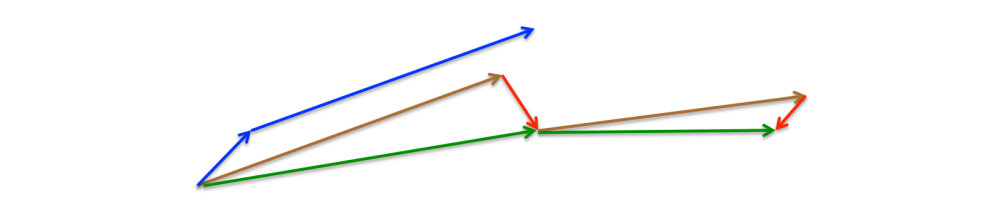
APG 与 NAG的结合
参考Data-Driven Sparse Structure Selection for Deep Neural Networks论文,其实也就是一个简单的上文提到的Lasso 问题的变种,定义如下目标函数,优化 x \mathbf{x} x,
min x g ( x ) + γ ∣ ∣ x ∣ ∣ 1 \begin{align} \min_{\bf{x}} g(\bf{x})+\gamma ||\bf{x}||_1 \end{align} xming(x)+γ∣∣x∣∣1
其中 g ( x ) g(\bf{x}) g(x)可微,则是一个典型的PGD优化问题,这里采用APG(加速近端梯度)进行优化。
根据APG算法,篇一公式(14)(15),可得,
d ( k ) = x ( k − 1 ) + k − 2 k + 1 ( x ( k − 1 ) − x ( k − 2 ) ) x ( k ) = p r o x η k ( d ( k ) − η k ∇ g ( d ( k ) ) ) f o r k = 1 , 2 , 3 , … \begin{align} d^{(k)} &= x^{(k-1)} + \frac{k-2}{k+1}(x^{(k-1)}-x^{(k-2)}) \\ x^{(k)}&=prox_{\eta_k}(d^{(k)}-\eta_k \nabla g(d^{(k)})) \\ for \space k&= 1,2,3,\ldots \nonumber \end{align} d(k)x(k)for k=x(k−1)+k+1k−2(x(k−1)−x(k−2))=proxηk(d(k)−ηk∇g(d(k)))=1,2,3,…
其中, η k \eta_k ηk代表学习率。
定义近端算子 / Soft-thresholding operator,参考篇一公式(9), 令 p r o x η k ( ⋅ ) = S γ η ( ⋅ ) prox_{\eta_k} (\cdot)= S_{\gamma\eta} ( \cdot ) proxηk(⋅)=Sγη(⋅),则
x ( k ) = S γ η ( k ) ( d ( k ) − η k ∇ g ( d ( k ) ) ) f o r k = 1 , 2 , 3 , … \begin{align} x^{(k)}&=S_{\gamma\eta_{(k)}}(d^{(k)}-\eta_k \nabla g(d^{(k)})) \\ for \space k&= 1,2,3,\ldots \nonumber \end{align} x(k)for k=Sγη(k)(d(k)−ηk∇g(d(k)))=1,2,3,…
然而,在深度学习中,这种操作是不友好的,计算 ∇ g ( d ( k ) ) \nabla g(d^{(k)}) ∇g(d(k)) 要额外对网络进行forward-backward运算。因此,作者他们想了个优化的方法,
首先对公式(2),公式(4)做了一个变形,
d ( k ) = x ( k − 1 ) + k − 2 k + 1 ( x ( k − 1 ) − x ( k − 2 ) ) ⟶ d ( k ) = x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) \begin{align} d^{(k)} &= x^{(k-1)} + \frac{k-2}{k+1}(x^{(k-1)}-x^{(k-2)}) \nonumber \\ \longrightarrow d^{(k)}&=x^{(k-1)} +\mu^{(k-1)} v^{(k-1)} \end{align} d(k)⟶d(k)=x(k−1)+k+1k−2(x(k−1)−x(k−2))=x(k−1)+μ(k−1)v(k−1)
同时对公式(4)中的 d ( k ) − η k ∇ g ( d ( k ) ) d^{(k)} -\eta_k \nabla g(d^{(k)}) d(k)−ηk∇g(d(k)) 作出如下变形,
z ( k ) = d ( k ) − η k ∇ g ( d ( k ) ) ⟶ z ( k ) = x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) − η k ∇ g ( x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) ) \begin{align} z^{(k)} &= d^{(k)} -\eta_k \nabla g(d^{(k)}) \nonumber \\ \longrightarrow z^{(k)}&=x^{(k-1)} +\mu^{(k-1)} v^{(k-1)} -\eta_k \nabla g(x^{(k-1)} +\mu^{(k-1)} v^{(k-1)} ) \end{align} z(k)⟶z(k)=d(k)−ηk∇g(d(k))=x(k−1)+μ(k−1)v(k−1)−ηk∇g(x(k−1)+μ(k−1)v(k−1))
则有,
v ( k ) = S γ η ( k ) ( z ( k ) ) − x ( k − 1 ) x ( k ) = x ( k − 1 ) + v ( k ) \begin{align} v^{(k)} &= S_{\gamma\eta_{(k)}}(z^{(k)}) - x^{(k-1)} \\ x^{(k)} &= x^{(k-1)}+v^{(k)}\end{align} v(k)x(k)=Sγη(k)(z(k))−x(k−1)=x(k−1)+v(k)
其中,另 μ ( k − 1 ) = k − 2 t + 1 \mu^{(k-1)}=\frac{k-2}{t+1} μ(k−1)=t+1k−2 , 另 v ( t k − 1 ) = x ( k − 1 ) − x ( k − 2 ) v^{(tk-1)} = x^{(k-1)}-x^{(k-2)} v(tk−1)=x(k−1)−x(k−2)。
那么为了避免计算 ∇ g ( x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) ) \nabla g(x^{(k-1)} +\mu^{(k-1)} v^{(k-1)}) ∇g(x(k−1)+μ(k−1)v(k−1))时造成的时长浪费,作者着重对 x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) x^{(k-1)} +\mu^{(k-1)} v^{(k-1)} x(k−1)+μ(k−1)v(k−1)进行了一个替代,即另 x ′ ( k − 1 ) = x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) x'^{(k-1)}=x^{(k-1)} +\mu^{(k-1)} v^{(k-1)} x′(k−1)=x(k−1)+μ(k−1)v(k−1),可以得到,
z ( k ) = x ′ ( k − 1 ) − η k ∇ g ( x ′ ( k − 1 ) ) v ( k ) = S γ η ( k ) ( z ( k ) ) − x ′ ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) x ′ ( k ) = S γ η ( k ) ( z ( k ) ) + μ ( k ) v ( k ) \begin{align} z^{(k)} &= x'^{(k-1)} -\eta_k \nabla g(x'^{(k-1)}) \\ v^{(k)} &= S_{\gamma\eta_{(k)}}(z^{(k)}) - x'^{(k-1)} +\mu^{(k-1)} v^{(k-1)} \\ x'^{(k)} &= S_{\gamma\eta_{(k)}}(z^{(k)}) +\mu^{(k)}v^{(k)} \end{align} z(k)v(k)x′(k)=x′(k−1)−ηk∇g(x′(k−1))=Sγη(k)(z(k))−x′(k−1)+μ(k−1)v(k−1)=Sγη(k)(z(k))+μ(k)v(k)
则计算 ∇ g ( x ′ ( k − 1 ) ) \nabla g(x'^{(k-1)}) ∇g(x′(k−1))将无需二次进行forward-backward运算。公式(11)的推导放在附录中。
最后还有一个软阈值/近端算子 S γ η ( k ) S_{\gamma\eta_{(k)}} Sγη(k)的定义,根据篇一,其定义如下:
S γ η ( k ) ( z ) i = s i g n ( z i ) R e L U ( ∣ z i ∣ − η ( k ) γ ) \begin{align} S_{\gamma\eta_{(k)}} (\mathbf{z})_i= sign(z_i)ReLU(|z_i|-\eta_{(k)}\gamma) \end{align} Sγη(k)(z)i=sign(zi)ReLU(∣zi∣−η(k)γ)
等价于,
S γ η ( k ) ( z ) i = s i g n ( z i ) M a x ( 0 , ∣ z i ∣ − η ( k ) γ ) \begin{align} S_{\gamma\eta_{(k)}} (\mathbf{z})_i= sign(z_i)Max(0,|z_i|-\eta_{(k)}\gamma) \end{align} Sγη(k)(z)i=sign(zi)Max(0,∣zi∣−η(k)γ)
Pytorch 代码实现
原论文中给出了mxnet的代码实现,但是mxnet框架有点老了,没用过也,遂迁移到pytorch。
原始代码:
import mxnet as mx
def apg_updater(weight, lr, grad, mom, gamma):
z = weight - lr * grad
z = soft_thresholding(z, lr * gamma)
mom[:] = z - weight + 0.9 * mom
weight[:] = z + 0.9 * mom
def soft_thresholding(x, gamma):
y = mx.nd.maximum(0, mx.nd.abs(x) - gamma)
return mx.nd.sign(x) * y
迁移后代码:
class APGNAG(Optimizer):
r"""Implements nesterov accelerated gradient descent with APG(optionally with momentum).
"""
def __init__(self, params, lr=required, momentum=0, dampening=0,
weight_decay=0, nesterov=False, gamma=None):
if lr is not required and lr < 0.0:
raise ValueError("Invalid learning rate: {}".format(lr))
if momentum < 0.0:
raise ValueError("Invalid momentum value: {}".format(momentum))
if weight_decay < 0.0:
raise ValueError("Invalid weight_decay value: {}".format(weight_decay))
defaults = dict(lr=lr, momentum=momentum, dampening=dampening,
weight_decay=weight_decay, nesterov=nesterov)
if nesterov and (momentum <= 0 or dampening != 0):
raise ValueError("Nesterov momentum requires a momentum and zero dampening")
self.gamma = gamma
super(APGNAG, self).__init__(params, defaults)
def __setstate__(self, state):
super(APGNAG, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('nesterov', False)
def step(self, closure=None):
"""Performs a single optimization step.
Arguments:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
weight_decay = group['weight_decay']
momentum = group['momentum']
dampening = group['dampening']
nesterov = group['nesterov']
for p in group['params']:
if p.grad is None:
continue
d_p = p.grad.data #* 参数的一阶梯度
# update weight_decay
if weight_decay != 0:
d_p.add_(p.data, alpha=weight_decay ) #* d_p = d_p + weight_decay * p.data
# update momentum
if momentum != 0:
param_state = self.state[p]
if 'momentum_buffer' not in param_state:
buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
else:
buf = param_state['momentum_buffer']
z = p.data.add(d_p, alpha = -group['lr']) #* z = p.data - lr * d_p
z = self.soft_thresholding(z, group['lr'] * self.gamma) #* S = soft_thresholding(z, lr * gamma)
buf = z - p.data + buf * momentum #* v = S - p.data + momentum * buf buf: v_{t-1} momentum: \mu
p.data = z + momentum * buf #* p.data = S + momentum * buf
#no negtive
p.data = torch.max(p.data, torch.zeros_like(p.data).cuda())
return loss
@staticmethod
def soft_thresholding(x, gamma):
return torch.sign(x) * torch.max(torch.abs(x) - gamma, torch.zeros_like(x).cuda())
总结
附录
公式(11)推导
根据公式(8),已知, x ( k ) = x ( k − 1 ) + v ( k ) x^{(k)} = x^{(k-1)}+v^{(k)} x(k)=x(k−1)+v(k),且 x ′ ( k − 1 ) = x ( k − 1 ) + μ ( k − 1 ) v ( k − 1 ) x'^{(k-1)}=x^{(k-1)} +\mu^{(k-1)} v^{(k-1)} x′(k−1)=x(k−1)+μ(k−1)v(k−1),则
x ′ ( k ) = x ( k ) + μ ( k ) v ( k ) = x ( k − 1 ) + v ( k ) + μ ( k ) v ( k ) = x ′ ( k − 1 ) − μ ( k − 1 ) v ( k − 1 ) + v ( k ) + μ ( k ) v ( k ) A c c o r d i n g t o f o r m u l a ( 10 ) , g e t : = S γ η ( k ) ( z ( k ) ) − v ( k ) + μ ( k − 1 ) v ( k − 1 ) − μ ( k − 1 ) v ( k − 1 ) + v ( k ) + μ ( k ) v ( k ) = S γ η ( k ) ( z ( k ) ) + μ ( k ) v ( k ) \begin{aligned} x'(k) &= x(k)+\mu^{(k)} v^{(k)} \\ &= x^{(k-1)}+v^{(k)}+ \mu^{(k)} v^{(k)} \\ &= x'^{(k-1)} - \mu^{(k-1)} v^{(k-1)} +v^{(k)}+ \mu^{(k)} v^{(k)} \\ &According \space to \space formula (10), get: \\ &= S_{\gamma\eta_{(k)}}(z^{(k)}) - v^{(k)} +\mu^{(k-1)} v^{(k-1)} - \mu^{(k-1)} v^{(k-1)} +v^{(k)}+ \mu^{(k)} v^{(k)} \\ &= S_{\gamma\eta_{(k)}}(z^{(k)}) +\mu^{(k)}v^{(k)} \end{aligned} x′(k)=x(k)+μ(k)v(k)=x(k−1)+v(k)+μ(k)v(k)=x′(k−1)−μ(k−1)v(k−1)+v(k)+μ(k)v(k)According to formula(10),get:=Sγη(k)(z(k))−v(k)+μ(k−1)v(k−1)−μ(k−1)v(k−1)+v(k)+μ(k)v(k)=Sγη(k)(z(k))+μ(k)v(k)