
【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

专栏详细介绍:【深度学习入门到进阶】必看系列,含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等
本专栏主要方便入门同学快速掌握相关知识。声明:部分项目为网络经典项目方便大家快速学习,后续会不断增添实战环节(比赛、论文、现实应用等)
专栏订阅:深度学习入门到进阶专栏
1.学习率
学习率是训练神经网络的重要超参数之一,它代表在每一次迭代中梯度向损失函数最优解移动的步长,通常用 η \eta η表示。它的大小决定网络学习速度的快慢。在网络训练过程中,模型通过样本数据给出预测值,计算代价函数并通过反向传播来调整参数。重复上述过程,使得模型参数逐步趋于最优解从而获得最优模型。在这个过程中,学习率负责控制每一步参数更新的步长。合适的学习率可以使代价函数以合适的速度收敛到最小值。
1.1 学习率对网络的影响
梯度更新公式: θ = θ − η ∂ ∂ θ J ( θ ) \theta=\theta-\eta\frac{\partial}{\partial\theta}J(\theta) θ=θ−η∂θ∂J(θ)
根据上述公式我们可以看到,如果学习率 η \eta η较大,那么参数的更新速度就会很快,可以加快网络的收敛速度,但如果学习率过大,可能会导致参数在最优解附近震荡,代价函数难以收敛,甚至可能会错过最优解,导致参数向错误的方向更新,代价函数不仅不收敛反而可能爆炸(如图1a所示)。如果学习率 η \eta η较小,网络可能不会错过最优点,但是网络学习速度会变慢。同时,如果学习率过小,则很可能会陷入局部最优点(如图1b所示)。因此,只有找到合适的学习率,才能保证代价函数以较快的速度逼近全局最优解。
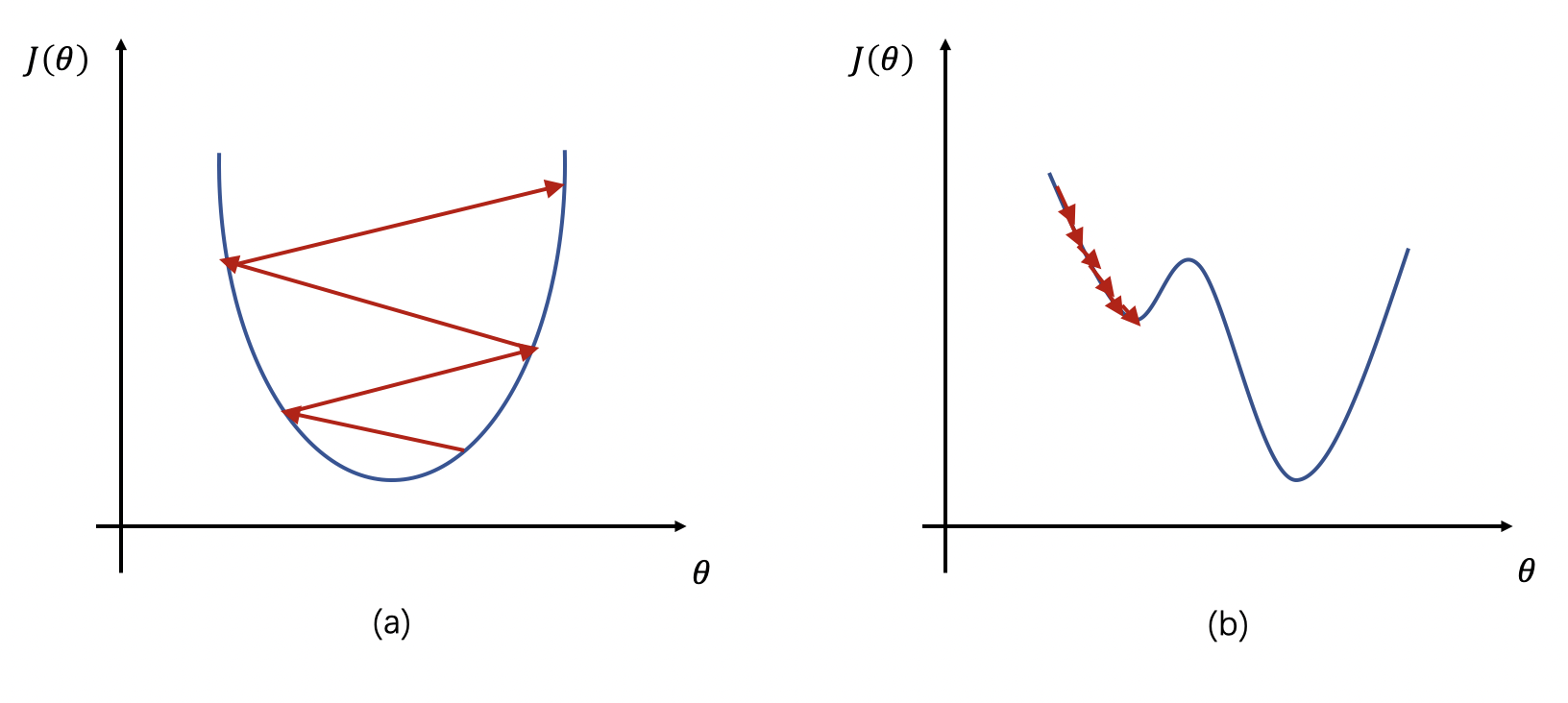
1.2学习率的设置
我们了解了只有合适的学习率才能保证网络稳定学习的同时,又以合理的高速收敛来减少训练时间。那么,如何设置学习率呢?
**
通常的,在训练网络的前期过程中,会选取一个相对较大的学习率以加快网络的收敛速度。而随着迭代优化的次数增多,逐步减小学习率,以保证最终收敛至全局最优解,而不是在其附近震荡或爆炸**。下面将介绍几种常用的学习率衰减方法,包括:分段常数衰减、指数衰减、自然指数衰减、多项式衰减、间隔衰减、多间隔衰减、逆时间衰减、Lambda衰减、余弦衰减、诺姆衰减、loss自适应衰减、线性学习率热身等。
1.2.1 分段常数衰减(Piecewise Decay)
在不同的学习阶段指定不同的学习率,在每段内学习率相同。该过程可以举例说明为:
boundaries = [100, 200] # 指定学习率改变的边界点为100和200
values = [1.0, 0.5, 0.1] # 指定不同区间下的学习率大小
learning_rate = 1.0 if epoch < 100
learning_rate = 0.5 if 100 <= epoch < 200
learning_rate = 0.1 if epoch >= 200
1.2.2 指数衰减(Exponential Decay)
学习率随训练轮数成指数衰减,每次将当前学习率乘以给定的衰减率得到下一个学习率。指数衰减的公式可表示为:
n e w _ l e a r n i n g _ r a t e = l a s t _ l e a r n i n g _ r a t e ∗ g a m m a new\_learning\_rate=last\_learning\_rate\ast gamma new_learning_rate=last_learning_rate∗gamma
其中,gamma为衰减率。
1.2.3 自然指数衰减 (Natural Exponential Decay)
每次将当前学习率乘以给定的衰减率的自然指数得到下一个学习率。其公式表达为:
KaTeX parse error: Expected 'EOF', got '_' at position 12: \textit{new_̲learning_rate}=…
其中,learning_rate为初始学习率,gamma为衰减率,epoch为训练轮数。
1.2.4多项式衰减(Polynomial Decay)
通过多项式衰减函数,学习率从初始值逐渐衰减至最低学习率。其中,参数 cycle表学习率下降后是否重新上升。若 cycle=True,则学习率衰减至最低后会重新上升到一定值,再降低至最低学习率并进行循环。若 cycle=False,则学习率从初始值单调递减至最低值。
- 若 cycle=True,其计算公式为:
d e c a y _ s t e p s = d e c a y _ s t e p s ∗ m a t h . c e i l ( e p o c h d e c a y _ s t e p s ) decay\_steps=decay\_steps*math.ceil(\dfrac{epoch}{decay\_steps})\quad\text{} decay_steps=decay_steps∗math.ceil(decay_stepsepoch)
n e w _ l e a r n i n g _ r a t e = ( l e a r n i n g _ r a t e − e n d _ l r ) ∗ ( 1 − e p o c h d e c a y _ s t e p s ) p o w e r + e n d _ l r new\_learning\_rate=(learning\_rate-end\_lr)*(1-\dfrac{epoch}{decay\_steps})^{power}+end\_lr new_learning_rate=(learning_rate−end_lr)∗(1−decay_stepsepoch)power+end_lr
- 若 cycle=False,其计算公式为:
e p o c h = m i n ( e p o c h , d e c a y steps ) epoch=min(epoch,decay\textit{steps}) epoch=min(epoch,decaysteps)
n e w _ l e a r n i n g _ r a t e = ( l e a r n i n g _ r a t e − e n d _ l r ) ∗ ( 1 − e p o c h d e c a y _ s t e p s ) p o w e r + e n d _ l r new\_learning\_rate=(learning\_rate-end\_lr)*(1-\dfrac{epoch}{decay\_steps})^{power}+end\_lr new_learning_rate=(learning_rate−end_lr)∗(1−decay_stepsepoch)power+end_lr
其中,learning_rate为初始学习率,decay_step为进行衰减的步长,end_lr为最低学习率,power为多项式的幂。
1.2.5 间隔衰减 (Step Decay)
学习率按照指定的轮数间隔进行衰减,该过程可举例说明为:
learning_rate = 0.5 # 学习率初始值
step_size = 30 # 每训练30个epoch进行一次衰减
gamma = 0.1 # 衰减率
learning_rate = 0.5 if epoch < 30
learning_rate = 0.05 if 30 <= epoch < 60
learning_rate = 0.005 if 60 <= epoch < 90
1.2.6 多间隔衰减(Multi Step Decay)
学习率按特定间隔进行衰减,与间隔衰减的区别在于:间隔衰减的epoch间隔是单一且固定的,而多间隔衰减中的epoch间隔是预先指定的多间隔。该过程可举例说明为:
learning_rate = 0.5 # 学习率初始值
milestones = [30, 50] # 指定轮数间隔
gamma = 0.1 # 衰减率
learning_rate = 0.5 if epoch < 30
learning_rate = 0.05 if 30 <= epoch < 50
learning_rate = 0.005 if 50 <= epoch
...
1.2.7 逆时间衰减(Inverse Time Decay)
学习率大小与当前衰减次数成反比。其计算公式如下:
n e w _ l e a r n i n g _ r a t e = l e a r n i n g _ r a t e 1 + g a m m a ∗ e p o c h new\_learning\_rate=\frac{l e a r n i n g\_r a t e}{1+g a m m a\ast e p o c h} new_learning_rate=1+gamma∗epochlearning_rate
其中,learning_rate为初始学习率,gamma为衰减率,epoch为训练轮数。
1.2.8 Lambda衰减(Lambda Decay)
使用lambda函数来设置学习率,其中lambda函数通过epoch计算出一个因子,使用该因子乘以初始学习率。该衰减过程可参考如下例子:
learning_rate = 0.5 # 学习率初始值
lr_lambda = lambda epoch: 0.95 ** epoch # 定义lambda函数
learning_rate = 0.5 # 当epoch = 0时,0.5 * 0.95 ** 0 = 0.5
learning_rate = 0.475 # 当epoch = 1时,0.5 * 0.95 ** 1 = 0.475
learning_rate = 0.45125 # 当epoch = 2时,0.5 * 0.95 ** 2 = 0.45125
...
1.2.9 余弦衰减(Cosine Annealing Decay)
使用 cosine annealing 的策略来动态调整学习率,学习率随step数变化成余弦函数周期变化。该方法为论文 SGDR:Stochastic Gradient Descent with Warm Restarts 中cosine annealing动态学习率。学习率调整公式为
\eta_t=\eta_{min}+\dfrac{1}{2}(\eta_{max}-\eta_{min})(1+cos(\dfrac{T_{car}}{T_{max}}\pi)),\quad T_{car}\neq(2k+1)T_{max}
\eta_{t+1}=\eta_t+\dfrac{1}{2}(\eta_{max}-\eta_{min})(1-cos(\dfrac{1}{T_{max}}\pi)),\quad T_{car}=(2k+1)T_{max}
1.2.10 诺姆衰减(Noam Decay)
诺姆衰减的计算方式如下:
n e w _ l e a r n i n g _ r a t e = l e a r n i n g _ r a t e ∗ d m o d e − 0.5 ∗ m i n ( e p s i l − 0.5 , e p o c h ∗ u a r m i p _ s t e p s − 1.5 ) new\_learning\_rate=learning\_rate\ast d^{-0.5}_{mode}\ast min(epsil^{-0.5},epoch\ast uarmip\_steps^{-1.5}) new_learning_rate=learning_rate∗dmode−0.5∗min(epsil−0.5,epoch∗uarmip_steps−1.5)
其中, d m o d e l d_model dmodel代表模型的输入、输出向量特征维度,warmup_steps为预热步数,learning_rate为初始学习率。更多细节请参考 attention is all you need。
1.2.11 loss自适应衰减(Reduce On Plateau)
当loss停止下降时,降低学习率。其思想是:一旦模型表现不再提升,将学习率降低 2-10 倍对模型的训练往往有益。此外,每降低一次学习率后,将会进入一个冷静期。在冷静期内不会监控loss变化也不会进行衰减。当冷静期结束后,会继续监控loss的上升或下降。
1.2.12 线性学习率热身(Linear Warm Up) 用的比较多
线性学习率热身是一种学习率优化策略,在正常调整学习率前,先逐步增大学习率。
当训练步数小于热身步数(warmup_steps)时,学习率 l r lr lr按如下方式更新:
l r = s t a r t _ l r + ( e n d _ l r − s t a r t _ l r ) ∗ e p o c h w a r m u p _ s t e p s lr=start\_lr+(end\_lr-start\_lr)*\dfrac{epoch}{warmup\_steps}\quad lr=start_lr+(end_lr−start_lr)∗warmup_stepsepoch
当训练步数大于等于热身步数(warmup_steps)时,学习率 l r lr lr为:
l r = l e a r n i n g _ r a t e lr=learning\_rate lr=learning_rate
其中,lr为热身之后的学习率,start_lr为学习率初始值,end_lr为最终学习率,epoch为训练轮数。
2.batch size
2.1 什么是BatchSize
- Batch一般被翻译为批量,设置batch_size的目的让模型在训练过程中每次选择批量的数据来进行处理。Batch Size的直观理解就是一次训练所选取的样本数。
- Batch Size的大小影响模型的优化程度和速度。同时其直接影响到GPU内存的使用情况,假如你GPU内存不大,该数值最好设置小一点。
在神经网络的训练过程中,一个非常直观的需要调整的超参数就是batch size。我们需要决定在一次训练中,要选取多少样本喂给神经网络,这个要选择的样本个数,就是batch size。batch size的可取值范围为1到全体样本数。举个例子,
- 传统的梯度下降法(Gradient Descent)就是采用了全部样本来进行训练和梯度更新,
- 它的变体随机梯度下降法(stochastic gradient descent),则设定batch size为1,即每次只将一个样本喂给神经网络,
- 在mini-batch梯度下降法中,则采用了一个折中的方法,每次选择一部分数据用于训练
2.2 batch size对网络的影响
-
在没有使用Batch Size之前,这意味着网络在训练时,是一次把所有的数据(整个数据库)输入网络中,然后计算它们的梯度进行反向传播,由于在计算梯度时使用了整个数据库,所以计算得到的梯度方向更为准确。但在这情况下,计算得到不同梯度值差别巨大,难以使用一个全局的学习率,所以这时一般使用Rprop这种基于梯度符号的训练算法,单独进行梯度更新。
-
在小样本数的数据库中,不使用Batch Size是可行的,而且效果也很好。但是一旦是大型的数据库,一次性把所有数据输进网络,肯定会引起内存的爆炸。所以就提出Batch Size的概念。
-
当采取传统的梯度下降法时,神经网络每一次训练都会使用全部数据。梯度基于全样本计算,因此会很准确。对于凸问题,局部最优即为全局最优的情况下,准确的梯度计算可以使梯度更新朝着正确的方向进行,以较快的速度达到全局最优解。但在真实的神经网络训练过程中,我们通常遇到的都是非凸问题,此时,局部最优解不是全局最优解,而传统的梯度下降法在这种情况下很容易陷入局部最优点或鞍点。同时,当整体样本数不大时,采用全体样本做batch size不会非常耗时,而当样本数很大时,每一次的计算将会非常耗时,也会导致内存爆炸。
-
当采取随机梯度下降法时,batch size值为1,每次获得的梯度都是根据当前的随机样本计算得来。由一个样本的梯度来近似所有的样本,会导致梯度估计不是很准确。同时,梯度易收到极端值的影响,导致损失剧烈震荡。但因为batch size为1,随机梯度下降法的计算速度会非常快。
-
如果选取比较折中的batch size作为mini-batch来进行随机梯度下降,其优点是用部分样本来近似全部样本,梯度相对于batch size为1更为准确,同时相比与使用全部样本,计算量减小,计算速度和收敛速度都会得到提升。看到这里可能会有一个疑问,为什么10000样本训练1次会比100样本训练100次收敛慢呢?我们假设样本真实的标准差为 σ \sigma σ,则 n个样本均值的标准差为 σ n \frac{\sigma}{\sqrt{n}} nσ, n \sqrt{n} n表明使用更多样本来估计梯度的方法回报是低于线性的。10000个样本训练一次和100个样本训练一次,由于计算量是线性的,前者的计算量是后者的100倍,但均值标准差只比后者降低了10倍,那么在相同的计算量下(同样训练10000个样本),小样本的收敛速度是远快于使用整个样本集的。同时,相对于训练全部样本,由于梯度存在不准确性,噪声的影响很可能会让梯度下降的过程中离开局部最优点或鞍点,从而有机会寻找全局最优点。
2.3 如何设置Batch_Size 的值?
更大的batch size会得到更精确的梯度估计值,但其估计梯度的回报是低于线性的。如果训练集较小,可以直接使用梯度下降法,batch size等于样本集大小。
设置BatchSize要注意一下几点:
1)batch数太小,而类别又比较多的时候,真的可能会导致loss函数震荡而不收敛,尤其是在你的网络比较复杂的时候。
2)随着batchsize增大,处理相同的数据量的速度越快。
3)随着batchsize增大,达到相同精度所需要的epoch数量越来越多。
4)由于上述两种因素的矛盾, Batch_Size 增大到某个时候,达到时间上的最优。
5)由于最终收敛精度会陷入不同的局部极值,因此 Batch_Size 增大到某些时候,达到最终收敛精度上的最优。
6)过大的batchsize的结果是网络很容易收敛到一些不好的局部最优点。同样太小的batch也存在一些问题,比如训练速度很慢,训练不容易收敛等。
7)具体的batch size的选取和训练集的样本数目相关。
8)GPU对2的幂次的batch可以发挥更佳的性能,因此设置成16、32、64、128…时往往要比设置为整10、整100的倍数时表现更优,Deep Learning 书中提到,在某些硬件上使用特定大小的数组时,运行时间会更少。尤其是在使用GPU时,通常使用2的幂数作为batch size可以获得更少的运行时间。
我在设置BatchSize的时候,首先选择大点的BatchSize把GPU占满,观察Loss收敛的情况,如果不收敛,或者收敛效果不好则降低BatchSize,一般常用16,32,64等。
2.3.1 在合理范围内,增大Batch_Size有何好处?
- 内存利用率提高了,大矩阵乘法的并行化效率提高。
- 跑完一次 epoch(全数据集)所需的迭代次数减少,对于相同数据量的处理速度进一步加快。
- 在一定范围内,一般来说 Batch_Size 越大,其确定的下降方向越准,引起训练震荡越小。
2.3.2 盲目增大 Batch_Size 有何坏处?
- 内存利用率提高了,但是内存容量可能撑不住了。
- 跑完一次 epoch(全数据集)所需的迭代次数减少,要想达到相同的精度,其所花费的时间大大增加了,从而对参数的修正也就显得更加缓慢。
- Batch_Size 增大到一定程度,其确定的下降方向已经基本不再变化。
2.3.3 调节 Batch_Size 对训练效果影响到底如何?
-
Batch_Size 太小,模型表现效果极其糟糕(error飙升)。
-
随着 Batch_Size 增大,处理相同数据量的速度越快。
-
随着 Batch_Size 增大,达到相同精度所需要的 epoch 数量越来越多。
-
由于上述两种因素的矛盾, Batch_Size 增大到某个时候,达到时间上的最优。
-
由于最终收敛精度会陷入不同的局部极值,因此 Batch_Size 增大到某些时候,达到最终收敛精度上的最优
- batchsize过小:每次计算的梯度不稳定,引起训练的震荡比较大,很难收敛。
batchsize过大优点:
-
(1)提高了内存利用率,大矩阵乘法并行计算效率提高。
-
(2)计算的梯度方向比较准,引起的训练的震荡比较小。
-
(3)跑完一次epoch所需要的迭代次数变小,相同数据量的数据处理速度加快。
batchsize过大缺点:
- 容易内容溢出,想要达到相同精度,epoch会越来越大,容易陷入局部最优,泛化性能差。
batchsize设置:通常10到100,一般设置为2的n次方。
原因:计算机的gpu和cpu的memory都是2进制方式存储的,设置2的n次方可以加快计算速度。
深度学习中经常看到epoch、 iteration和batchsize这三个的区别:
- batchsize:批大小。在深度学习中,一般采用SGD训练,即每次训练在训练集中取batchsize个样本训练;
- iteration:1个iteration等于使用batchsize个样本训练一次;
- epoch:1个epoch等于使用训练集中的全部样本训练一次;
举个例子,训练集有1000个样本,batchsize=10,那么训练完整个样本集需要:100次iteration,1次epoch。
1.当数据量足够大的时候可以适当的减小batch_size,由于数据量太大,内存不够。但盲目减少会导致无法收敛,batch_size=1时为在线学习,也是标准的SGD,这样学习,如果数据量不大,noise数据存在时,模型容易被noise带偏,如果数据量足够大,noise的影响会被“冲淡”,对模型几乎不影响。
2.batch的选择,首先决定的是下降方向,如果数据集比较小,则完全可以采用全数据集的形式。这样做的好处有两点,
1)全数据集的方向能够更好的代表样本总体,确定其极值所在。
2)由于不同权重的梯度值差别巨大,因此选取一个全局的学习率很困难。
3.参数初始化
在我们开始训练神经网络之前,首先要做的是给网络中的每一个权重和偏置赋值,这个赋值的过程就是参数初始化。合理的初始化可以缩短神经网络的训练时间,而不合理的初始化可能使网络难以收敛。那么,我们要如何对参数进行初始化呢?或许你有想到过将全部参数都设置为0,这看起来是一个简单又方便的办法,但遗憾的是神经网络中不能对权重进行全零初始化。在讨论如何对参数进行初始化前,我们先来看看为什么不能进行全零初始化。
为什么不能全零初始化?
以一个三层网络为例,假设其具体的网络示意图如图1所示。
其中, z 4 、 z 5 、 z 6 z4、z5、z6 z4、z5、z6可表达为:
z 4 = w 14 ∗ x 1 + w 24 ∗ x 2 + w 34 ∗ x 3 + b 4 z 5 = w 15 ∗ x 1 + w 25 ∗ x 2 + w 35 ∗ x 3 + b 5 z 6 = w 16 ∗ x 1 + w 26 ∗ x 2 + w 36 ∗ x 3 + b 6 z_4=w_{14}*x_1+w_{24}*x_2+w_{34}*x_3+b_4\\ z_5=w_{15}*x_1+w_{25}*x_2+w_{35}*x_3+b_5\\ z_6=w_{16}*x_1+w_{26}*x_2+w_{36}*x_3+b_6 z4=w14∗x1+w24∗x2+w34∗x3+b4z5=w15∗x1+w25∗x2+w35∗x3+b5z6=w16∗x1+w26∗x2+w36∗x3+b6
由于权重和偏置的初始值都为0,且同一层网络的激活函数相同,则有:
z 4 = z 5 = z 6 a 4 = a 5 = a 6 \begin{array}{c}z_4=z_5=z_6\\ a_4=a_5=a_6\end{array} z4=z5=z6a4=a5=a6
对于神经网络的最终输出 a 7 a_7 a7,我们可以得到:
z 7 = w 47 ∗ a 4 + w 57 ∗ a 5 + w 67 ∗ a 6 a 7 = f ( z 7 ) \begin{array}{l}z_7=w_{47}*a_4+w_{57}*a_5+w_{67}*a_6\\ a_7=f(z_7)\\ \end{array} z7=w47∗a4+w57∗a5+w67∗a6a7=f(z7)
其中, f ( ⋅ ) f(\cdot) f(⋅)为第三层网络的激活函数。
假设真实值为 y, 损失函数为 L o s s ( a 7 , y ) Loss(a_7,y) Loss(a7,y),根据反向传播算法和链式法则,我们可以得到:
∂ L o s s ( a 7 , y ) ∂ w 47 = ∂ L o s s ( a 7 , y ) ∂ a 7 ∗ ∂ a 7 ∂ z 7 ∗ ∂ z 7 ∂ w 47 = ∂ L o s s ( a 7 , y ) ∂ a 7 ∗ ∂ a 7 ∂ z 7 ∗ a 4 \begin{aligned}\frac{\partial Loss(a_7,y)}{\partial w_{47}}&=\frac{\partial Loss(a_7,y)}{\partial a_7}*\frac{\partial a_7}{\partial z_7}*\frac{\partial z_7}{\partial w_{47}}\\ &=\frac{\partial Loss(a_7,y)}{\partial a_7}*\frac{\partial a_7}{\partial z_7}*a_4\\ \end{aligned} ∂w47∂Loss(a7,y)=∂a7∂Loss(a7,y)∗∂z7∂a7∗∂w47∂z7=∂a7∂Loss(a7,y)∗∂z7∂a7∗a4
同样地:
∂ L o s s ( a 7 , y ) ∂ w 57 = ∂ L o s s ( a 7 , y ) ∂ a 7 ∗ ∂ a 7 ∂ z 7 ∗ ∂ z 7 ∂ w 67 = ∂ L o s s ( a 7 , y ) ∂ a 7 ∗ ∂ a 7 ∂ z 7 ∗ a 5 ∂ L o s s ( a 7 , y ) ∂ w 37 = ∂ L o s s ( a 7 , y ) ∂ a 7 ∗ ∂ a 7 ∂ z 7 ∗ a 6 \begin{aligned}\frac{\partial Loss(a_{7},y)}{\partial w_{57}}&=\frac{\partial Loss(a_{7},y)}{\partial a_{7}}*\frac{\partial a_{7}}{\partial z_{7}}*\frac{\partial z_{7}}{\partial w_{67}}\\ &=\frac{\partial Loss(a_{7},y)}{\partial a_{7}}*\frac{\partial a_{7}}{\partial z_{7}}*a_{5}\\ \frac{\partial Loss(a_{7},y)}{\partial w_{37}}=\frac{\partial Loss(a_{7},y)}{\partial a_{7}}*\frac{\partial a_{7}}{\partial z_{7}}*a_{6}\end{aligned} ∂w57∂Loss(a7,y)∂w37∂Loss(a7,y)=∂a7∂Loss(a7,y)∗∂z7∂a7∗a6=∂a7∂Loss(a7,y)∗∂z7∂a7∗∂w67∂z7=∂a7∂Loss(a7,y)∗∂z7∂a7∗a5
由于 a 4 = a 5 = a 6 a_4=a_5=a_6 a4=a5=a6,则有:
∂ L o s s ( a 7 , y ) ∂ w 47 = ∂ L o s s ( a 7 , y ) ∂ w 57 = ∂ L o s s ( a 7 , y ) ∂ w 67 = Δ w \frac{\partial L o s s(a_7,y)}{\partial w_{47}}=\frac{\partial L o s s(a_7,y)}{\partial w_{57}}=\frac{\partial L o s s(a_7,y)}{\partial w_{67}}=\Delta w\quad ∂w47∂Loss(a7,y)=∂w57∂Loss(a7,y)=∂w67∂Loss(a7,y)=Δw
权重更新表达式为:
w 47 ′ = w 47 + Δ w w 57 ′ = w 57 + Δ w w 67 ′ = w 67 + Δ w \begin{array}{c}w'_{47}=w_{47}+\Delta w\\ w'_{57}=w_{57}+\Delta w\\ w'_{67}=w_{67}+\Delta w\end{array} w47′=w47+Δww57′=w57+Δww67′=w67+Δw
由于 w 47 、 w 57 、 w 67 w_{47}、w_{57}、w_{67} w47、w57、w67的初始值均为0,那么: w ′ 47 = w ′ 57 = w ′ 67 w′_{47}=w′_{57}=w′_{67} w′47=w′57=w′67,同理: w ′ 14 = w ′ 24 = w ′ 34 = w ′ 14 = w ′ 25 = w ′ 26 = w ′ 34 = w ′ 35 = w ′ 36 w′_{14}=w′_{24}=w′_{34}=w′_{14}=w′_{25}=w′_{26}=w′_{34}=w′_{35}=w′_{36} w′14=w′24=w′34=w′14=w′25=w′26=w′34=w′35=w′36
。由此可见,更新后的参数在每一层内都是相同的。同时,无论经过多少次网络训练,相同网络层内的参数值都是相同的,这会导致网络在学习时没有重点,对所有的特征处理相同,这很可能导致模型无法收敛训练失败。这种现象被称为对称失效。
3. 常见的初始化方法
3.1 基于固定方差的参数初始化
一种非常常见的方式是采用高斯分布或均匀分布来对权重进行随机初始化。高斯分布和均匀分布的选择似乎没有很大差别,但初始分布的大小对于优化过程的结果和网络泛化能力都有很大影响。
高斯分布初始化:使用一个均值为 μ \mu μ,方差为 σ 2 \sigma_{2} σ2的高斯分布 N(μ,σ2)对每个参数进行随机初始化,通常情况下,μ=0,并对生成的数乘上一个小数,把权重初始化为很小的随机数。比如: w = 0.01 ∗ n p . r a n d o m . r a n d ( D , H ) w=0.01∗np.random.rand(D,H) w=0.01∗np.random.rand(D,H),这里选择乘以0.01初始化为一个很小的数是因为,如果最初随机到的 w值很大,当我们选择 sigmoid 或 tanh 激活函数时,函数值 s i g m o i d ( ⋅ ) sigmoid(⋅) sigmoid(⋅)或 t a n h ( ⋅ ) tanh(⋅) tanh(⋅)会停留在一个很平坦的地方,激活值接近饱和,导致梯度下降时,梯度很小,学习变得缓慢。但也不是说权重值越小越好,如果权重值过小,会导致在反向传播时计算得到很小的梯度值,在不断的反向传播过程中,引起梯度消失。
均匀分布初始化:在一个给定区间 [−r,r]内采取均匀分布进行初始化。假设随机变量在区间 [a,b]内均匀分布,则其方差为 v a r ( x ) = ( b − a ) 2 12 . var(x)=\frac{\left(b-a\right)^2}{12}. var(x)=12(b−a)2.。因此,当在 [−r,r]的区间内均匀分布采样,并满足 v a r ( x ) = σ 2 var(x)=\sigma^{2} var(x)=σ2时,则有 r = 3 σ 2 . r=\sqrt{3\sigma^{2}}\text{.} r=3σ2.
上述两种基于固定方差的初始随机化方法中,关键点在于如何设置方差 σ 2 \sigma^{2} σ2。过大或过小的方差都会导致梯度下降缓慢,网络训练效果不好等问题。为了降低固定方差对网络性能及优化效率的影响,基于固定方差的随机初始化一般要配合逐层归一化来使用。
3.2 基于方差缩放的参数初始化
方差缩放方法能够根据神经元的链接数量来自适应地调整初始化分布地方差,尽可能的保证每个神经元的输入和输出方差一致。那么,为什么要保证前后方差的一致性呢?这是因为如果输入空间和输出空间的方差差别较大,也就是说数据空间分布差异较大,那么在反向传播时可能会引起梯度消失或爆炸问题。比如,当输入空间稀疏,输出空间稠密时,将在输出空间计算得到的误差反向传播给输入空间时,这个误差可能会显得微不足道,从而引起梯度消失。而当输入空间稠密,输出空间稀疏时,将误差反向传播给输入空间,就可能会引起梯度爆炸,使得模型震荡。
3.2.1 Xavier初始化
Xavier初始化的提出,遵循了Bradley(2009)的理论环境,假设网络中的每一层的激活函数都是关于0对称的线性激活函数,权重间的初始化和输入特征相互独立,且均值都为0。
假设在一个神经网络中,对于一层线性网络,其表示为:
y = f ( z 1 W 1 + z 2 W 2 + z 3 W 3 + . . . + z i W i + b ) y=f(z_1W_1+z_2W_2+z_3W_3+...+z_iW_i+b)\quad\text{} y=f(z1W1+z2W2+z3W3+...+ziWi+b)
z i z_i zi代表该层网络的第 i个神经元,y为该层网络的输出, W i W_i Wi为本层网络的权重,b为偏置, f ( ⋅ ) f(⋅) f(⋅)为激活函数。这里我们假设激活函数为恒等函数,即 f(x)=x,导数为1。
对于其中的每个 z i W i z_iW_i ziWi,其方差为:
V a r ( z i W i ) = E ( z i ) 2 V a r ( W i ) + E ( W i ) 2 V a r ( z i ) + V a r ( z i ) V a r ( W i ) Var(z_i W_i)=E(z_i)^2Var(W_i)+E(W_i)^2Var(z_i)+Var(z_i)Var(W_i) Var(ziWi)=E(zi)2Var(Wi)+E(Wi)2Var(zi)+Var(zi)Var(Wi)
由于 W i W_i Wi和 z i z_i zi的均值都为0,因此可以得到:
V a r ( z i W i ) = V a r ( z i ) V a r ( W i ) Var(z_iW_i)=Var(z_i)Var(W_i) Var(ziWi)=Var(zi)Var(Wi)
又因为 z z z和 W W W相互独立,则有:
V a r ( y ) = n i ∗ V a r ( z i ) V a r ( W i ) Var(y)=n_i*Var(z_i)Var(W_i)\quad\text{} Var(y)=ni∗Var(zi)Var(Wi)
其中, n i n_i ni代表第 i层的神经元数量。
通过上面的公式我们可以发现,输入 z i z_i zi的方差和输出 y方差相差 n ∗ V a r ( W i ) n∗Var(W_i) n∗Var(Wi)倍,也就是说输入信号在经过神经元后会被放大或缩小 n ∗ V a r ( W i ) n∗Var(W_i) n∗Var(Wi)倍。为保证经过多层网络后,信号不被过分的放大或缩小,我们需要尽可能保证前向传播和反向传播时每层方差保持一致,则有:
∀ i , n i ∗ V a r ( W i ) = 1 ∀ i , n i + 1 ∗ V a r ( W i ) = 1 \begin{matrix}\forall i,\quad n_i*Var(W_i)=1\\ \forall i,\quad n_{i+1}*Var(W_i)=1\end{matrix} ∀i,ni∗Var(Wi)=1∀i,ni+1∗Var(Wi)=1
权衡上述两个限制,提出一个折中的办法:
∀ i , V a r ( W i ) = 2 n i + n i + 1 \forall i,\quad Var(W_i)=\dfrac{2}{n_i+n_{i+1}} ∀i,Var(Wi)=ni+ni+12
根据计算出的理想方差,可选择通过高斯分布或均匀分布来随机初始化参数。若采用高斯分布,则权重可按照 N ( 0 , 2 n i + n i + 1 ) N(0,\frac{2}{n_{i}+n_{i+1}}) N(0,ni+ni+12)的高斯分布来进行初始化。若采用在区间 [−r,r]的均匀分布进行初始化,则初始化分布有:
W ∼ U [ − 6 n i + n i + 1 , 6 n i + n i + 1 ] W\sim U[-\frac{\sqrt6}{\sqrt{n_i+n_{i+1}}},\frac{\sqrt6}{\sqrt{n_i+n_{i+1}}}]\quad\text{} W∼U[−ni+ni+16,ni+ni+16]
Xavier 初始化因为基本保证了输入和输出的方差一致,使得样本空间和类别空间的分布差异相似,因此使得模型的训练速度和分类性能获得提升。但xavier初始化的推导基于激活函数是线性的假设,使其并不适合于ReLU、sigmoid等非线性激活函数。
具体论文参见:Understanding the difficulty of training deep feedforward neural networks
3.2.2 Kaiming初始化
kaiming初始化是一种针对ReLU的初始化方法,假定使用ReLU激活函数时,网络每一层都中有一半的神经元被激活,另一半为0,因此其分布的方差也近似为恒等函数的一半。这样在考虑前向传播和反向传播时则有:
∀ i , 1 2 n i ∗ V a r ( W i ) = 1 ∀ i , 1 2 n i + 1 ∗ V a r ( W i ) = 1 \begin{array}{c}{ {\forall i,\quad\frac{1}{2}n_{i}*V a r(W_{i})=1}}\\ { {\forall i,\quad\frac{1}{2}n_{i+1}*V a r(W_{i})=1}}\\ \end{array} ∀i,21ni∗Var(Wi)=1∀i,21ni+1∗Var(Wi)=1
W i W_i Wi的理想方差为:
∀ i , V a r ( W i ) = 2 n i \forall i,\quad Var(W_i)=\dfrac2{n_i}\quad\text{} ∀i,Var(Wi)=ni2
当采用高斯分布时,则权重可按照 N ( 0 , 2 n i ) N(0,\frac{2}{n_i}) N(0,ni2)的高斯分布来进行初始化。若采用在区间 [−r,r]的均匀分布进行初始化,则初始化分布有:
W ∼ U [ + 6 n i , 6 n i ] W\sim U[+\dfrac{\sqrt{6}}{\sqrt{n_i}},\dfrac{\sqrt{6}}{\sqrt{n_i}}] W∼U[+ni6,ni6]
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification