深入理解机器学习——类别不平衡学习（Imbalanced Learning）： 类别不平衡分布对传统分类器性能的影响机理

文章《类别不平衡学习（Imbalanced Learning）：常用技术概览》已经以样本分布图的形式为读者直观地呈现了类别不平衡分布的负面影响。然而，读者可能仍不清楚其对各传统分类器性能的影响机理。在本文中，将分别以朴素贝叶斯、支持向量机及极限学习机这三种常用的分类器为例，从其各自的独特构造出发，在理论上分析类别不平衡分布对它们性能的影响机理，从而使读者能对类别不平衡分布的危害有更加深刻的认识。

朴素贝叶斯

众所周知，朴素贝叶斯分类器是提出较早且应用较为广泛的一种分类模型。该模型具有较强的理论基础，主要理论依据为贝叶斯定理及特征条件独立假设理论。假设用于分类建模的训练集共包括$n$个样本$x_1,x_2,\cdots ,x_n$，且这些样本可被划分为互不相交的$M$个类别$c_1,c_2,\cdots ,c_M$，则对于一个新样本$x$，根据贝叶斯决策理论，其隶属于类别$c_i$的概率可由下式求得：
$$P(c_i|x)=\frac{P(x|c_i)P(c_i)}{P(x)}$$

其中，$P(c_i|x)$为后验概率，表示样本$x$被划分为类别$c_i$的可能性；$P(c_i)$为先验概率，它表示在全部训练样本中，类标为$c_i$的样本所占的比例；$P(x|c_i)$则被称为类条件概率，即统计归属于类别$c_i$的样本中，与$x$具有相同属性取值的样本比例；$P(x)$是用于归一化的证据因子，即统计整个训练集中所出现的与$x$具有相同属性取值的样本比例。显然，只要给定一个训练集，先验概率、类条件概率及证据因子均可直接统计得到，代入上式即可计算得出最终的后验概率。计算样本$x$隶属于每一类的后验概率，再通过下式即可判定其归属类别：
$$h(x)=\arg \underset{i=1,2,\cdots ,M}{\max }P(c_i|x)$$

也就是将样本$x$判归为能使其后验概率最大的类别。

在贝叶斯判别规则中，还有一个需要关注的问题，即类条件概率$P(x|c_i)$的计算问题。考虑到对于绝大多数的分类问题而言，其样本通常都包含不止一个属性，在此情况下，则显然类条件概率$P(x|c_i)$应被分解为多个属性的联合概率，若训练样本有限，那么就会导致$P(x|c_i)$在其分布区间中的大部分位置取值为零，这显然是不合理的，因为“未被观测到”和“出现概率为零”是截然不同的两个概念。另外，样本中各属性的取值也未必都是离散的，对于取值为连续区间的属性而言，频率更是难以通过“查数”来统计得出。对于上述问题，贝叶斯决策理论通常是采用极大似然估计法来解决的。采用该方法，可近似估计得出属性空间中的概率密度分布，再用对应点的概率密度来近似替代类条件概率$P(x|c_i)$的估计值。

不失一般性，假设待分类问题为二类不平衡问题，其中少数类为正类，类标表示为$c_{+}$，多数类为负类，其类标用$c_{-}$来表示，每个样本只含有一个属性$x$，且两类样本在该属性上均服从正态高斯分布）。由于先验概率$P(c_{+})，P(c_{-})$及类条件概率$P(x|c_{+})，P(x|c_{-})$均已知，则可调用贝叶斯公式，计算得出其后验概率，分别为：
$$\begin{array}{rl}P(x|c_{+})=& \frac{P(x|c_{+})P(c_{+})}{P(x)}\\ P(x|c_{-})=& \frac{P(x|c_{-})P(c_{-})}{P(x)}\end{array}$$

显然，当分类边界出现在两类后验概率相等位置时，即$P(c_{+}|x)=P(c_{-}|x)$，也就是$P(x|c_{+})P(c_{+})=P(x|c_{-})P(c_{-})$时，分类器的经验风险将会达到最小化。

从上图可看出，若训练集中的样本是类别平衡的，即两类具有相等的先验概率$P(c_{+})=P(x|c_{-})P(c_{-})$，则分类边界应出现在两类类条件概率相等的位置，即上图中最优边界的位置。而若训练集是类别分布不平衡的，即$P(c_{+})<P(x|c_{-})P(c_{-})$，则为了保证后验概率相等，即$P(x|c_{+})P(c_{+})=P(x|c_{-})P(c_{-})$，分类边界将必然会出现在一个少数类的类条件概率高于多数类的类条件概率的位置，如上图中实际边界的位置。显然，实际的分类边界偏离了最优边界的位置，它被更多地推向了少数类所在的区域。基于上述理论解释，贝叶斯决策的结果会受到样本类别不平衡分布的影响，且这种影响是负面的。从上图中也可以看出，两类样本的重叠程度越高，类别不平衡比率越大，则分类边界的偏离度也将越大。

支持向量机

支持向量机（Support Vector Machine, SVM）为Vapnik于1995年提出，在2000年前后迅速发展成为机器学习领域的热点技术之一。不同于传统的分类算法，支持向量机不再以经验风险最小化为训练目标，转而追求结构风险最小化。所谓结构风险最小化，可以通过下图的例子加以解释。

从上图中可以看出，这是一个典型的二分类问题，利用这两类样本进行分类器建模，可以得到无数分类面，并可保证这些分类面的训练精度均为百分之百。上图中为大家展示了上述分类面中的三个，可分别标记为$H_1,H_2,h_3$。从直观上看，显然$H_2$的视觉效果要更好一些，因为它与两类边界样本的距离是相同的，且在它的垂直方向上，两类样本间存在最大的间隔，这就能保证其对训练样本的局部扰动具有最强的容忍度，也可以说它有最强的泛化能力。故若采用0-1损失函数作为分类器建模的度量标准，上述三个分类面均可保证经验风险最小化，而若考虑结构风险最小化，分类面$H_2$无疑是唯一选择。

支持向量机建模的目标就是要在样本空间中找到那个能使结构风险达到最小化的分类面。这个分类面可通过如下的线性方程来描述：
$$w^{T}x+b=0$$

其中，$w$为法向量，它决定了分类超平面的方向；$b$表示位移项，其决定了分类超平面与原点间的距离。显然，任一分类超平面的位置均可由其法向量$w$及位移项$b$唯一确定。样本空间中任意样本$x$到超平面的距离可由下式计算：
$$r=\frac{w^{T}x+b}{||w||}$$

若超平面可将全部训练样本均正确分类，即对于训练集中任一样本$(x_i,y_i)$，若$y_i=+1$，则有$w^{T}x+b>0$；若$y_i=-1$，则有$w^{T}x+b<0$。此时，可令：
$$\{\begin{array}{rl}{w}^{T}x+b\ge +1,& y_i=+1\\ w^{T}x+b\le -1,& y_i=-1\end{array}$$

如下图所示，距离超平面最近的几个圈起来的训练样本点可使上式的等号成立，我们通常将它们称为“支持向量”。显然，两个异类支持向量到超平面的距离之和为：
$$r=\frac{2}{||w||}$$

该距离被称为“间隔（Margin）”。

支持向量机的目的就是要找到那个具有最大间隔的分类面，也就是要找到对应的约束参数$w$和$b$，使得$\frac{2}{||w||}$最大。要使$\frac{2}{||w||}$最大，实际上就是要使$||w||$最小，于是待解的优化式可以写为如下形式：
$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}||w|{|}^2\\ \text{s.t.}& y_i(w^T{x}_i+b)\ge 1,i=1,2,\cdots ,N\end{array}$$
上述优化式是一个典型的二次规划问题，可以通过拉格朗日乘子法求解。前文仅仅考虑了训练样本线性可分的情况，然而在实际应用中，这种情况并不常出现。若训练样本在样本空间中线性不可分，则可考虑采用核方法将样本映射到线性可分的高维空间，再对分类面进行求解。核函数可表示为如下形式：
$$\begin{array}{rl}K(x_i,x_j)& \le \varphi (x_i)\\ \varphi (x_j)& \ge \varphi (x_i{)}^T\varphi (x_j)\end{array}$$

同时，为了避免分类间隔过小，从而降低分类器的泛化性能，可考虑令部分训练样本不满足约束式，这可通过在优化式中加入惩罚因子$C$来实现，则上式可被改写为：
$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i\\ \text{s.t.}& y_i(w^T\varphi (x_I)+b)\ge 1-\xi ,i=1,2,\cdots ,N;\xi \ge 0\end{array}$$

其中，$\xi$称为“松弛因子”，用来表示其不满足约束式$y_i(w^T\varphi (x_I)+b)\ge 1$的程度。通过拉格朗日乘子法，上式的对偶形式可被写为如下形式，并进行求解：
$$\begin{array}{rl}\underset{\alpha }{\min }& \sum _{i=1}^m{\alpha }_i+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{y}_i{y}_k{\alpha }_i{\alpha }_{J}K(x_i,x_j)\\ \text{s.t.}& \sum _{i=1}^N{y}_i{\alpha }_i=0,\forall i:0\le {\alpha }_i\le C\end{array}$$

观察上式可以发现，任一样本的拉格朗日乘子项系数${\alpha }_i$均对应如下三类情况之一：

• ${\alpha }_i=0$：这意味着对应样本能被正确分类，且位于间隔线外
• $0<{\alpha }_i<C$：这意味着对应样本位于间隔线上，也就是支持向量。
• ${\alpha }_i=C$：这意味着对应样本位于两条间隔线之间，能否被正确分类是未知的。

下面考虑类别不平衡问题，假设$N$个训练样本可被划分为两类，其中少数类样本数为$N^{+}$，多数类样本数为$N^{-}$，显然有$N^{+}<N^{-}$，且有$N^{+}+N^{-}=N$。此外，分别采用$N_{\text{SV}}^{+}$及$N_{\text{SV}}^{-}$表示两类样本中的支持向量个数，$N_{\text{boundary}}^{+}$和$N_{\text{boundary}}^{-}$来表示两类样本中被置于间隔区域中的样本数。则根据上式，显然有：
$$\begin{array}{rl}\sum _{i=1}^N{\alpha }_i& =\sum _{y_i=+1}^N{\alpha }_i+\sum _{y_i=-1}^N{\alpha }_i\\ \sum _{y_i=+1}^N{\alpha }_i& =\sum _{y_i=-1}^N{\alpha }_i\end{array}$$

由于${\alpha }_i$的取值至多为$C$，故可推得如下两个不等式：
$$\begin{array}{rl}\sum _{y_i=+1}{\alpha }_i& \ge N_{\text{boundary}}^{+}\times C\\ \sum _{y_i=+1}{\alpha }_i& \le N_{\text{SV}}^{+}\times C\end{array}$$

即：
$$N_{\text{SV}}^{+}\times C\ge \sum _{y_i=+1}{\alpha }_i\ge N_{\text{boundary}}^{+}\times C$$

同理可得：
$$N_{\text{SV}}^{-}\times C\ge \sum _{y_i=-1}{\alpha }_i\ge N_{\text{boundary}}^{-}\times C$$

在此，不妨令${\sum }_{y_i=+1}^N{\alpha }_i={\sum }_{y_i=-1}^N{\alpha }_i=M$，则：
$$\begin{array}{r}\frac{N_{\text{SV}}^{+}}{N^{+}}\ge \frac{M}{N^{+}\times C}\ge \frac{N_{\text{boundary}}^{+}}{N^{+}}\\ \frac{N_{\text{SV}}^{-}}{N^{-}}\ge \frac{M}{N^{-}\times C}\ge \frac{N_{\text{boundary}}^{-}}{N^{-}}\end{array}$$

其中，$\frac{N_{\text{boundary}}^{+}}{N^{+}}$和$\frac{N_{\text{boundary}}^{-}}{N^{-}}$分别表示两类样本中位于间隔区域的样本比例，由于间隔区域中样本的预测类标不可控，故上述两个指标也可分别看做是对两类训练样本错误率的一种近似。又由于有$N^{+}<N^{-}$，故显然有$\frac{M}{N^{+}\times C}$和$\frac{M}{N^{-}\times C}$，即表明正类（少数类）错误率的上限要高于负类（多数类）错误率的上限。由此，不难得出如下结论：支持向量机的训练结果会受到样本类别分布不平衡的影响，且这种影响是负面的。此外，也可看出，两类样本的训练样本数差别越大，则其对应的错误率上限的差别也将越大，负面影响的效果也越大。实际上，由于SVM的分类面仅与少量的支持向量有关，故其与其他分类器相比，受类别不平衡分布的影响要相对小得多。

极限学习机

极限学习机（Rxtreme Learning Machine, ELM）由南洋理工大学的Huang等人于2006年正式提出，经过近十年的发展，已经成为机器学习领域的研究热点之一。不同于传统的误差反传（Back-Propagation, BP）算法，极限学习机通过随机指定隐层参数，并利用最小二乘法求解输出层权重的方式来训练单隐层前馈神经网络（Single-hidden Layer Feedback Network, SLFN），故其具有泛化能力强、训练速度快等优点。SLFN的基本结构如下图所示：

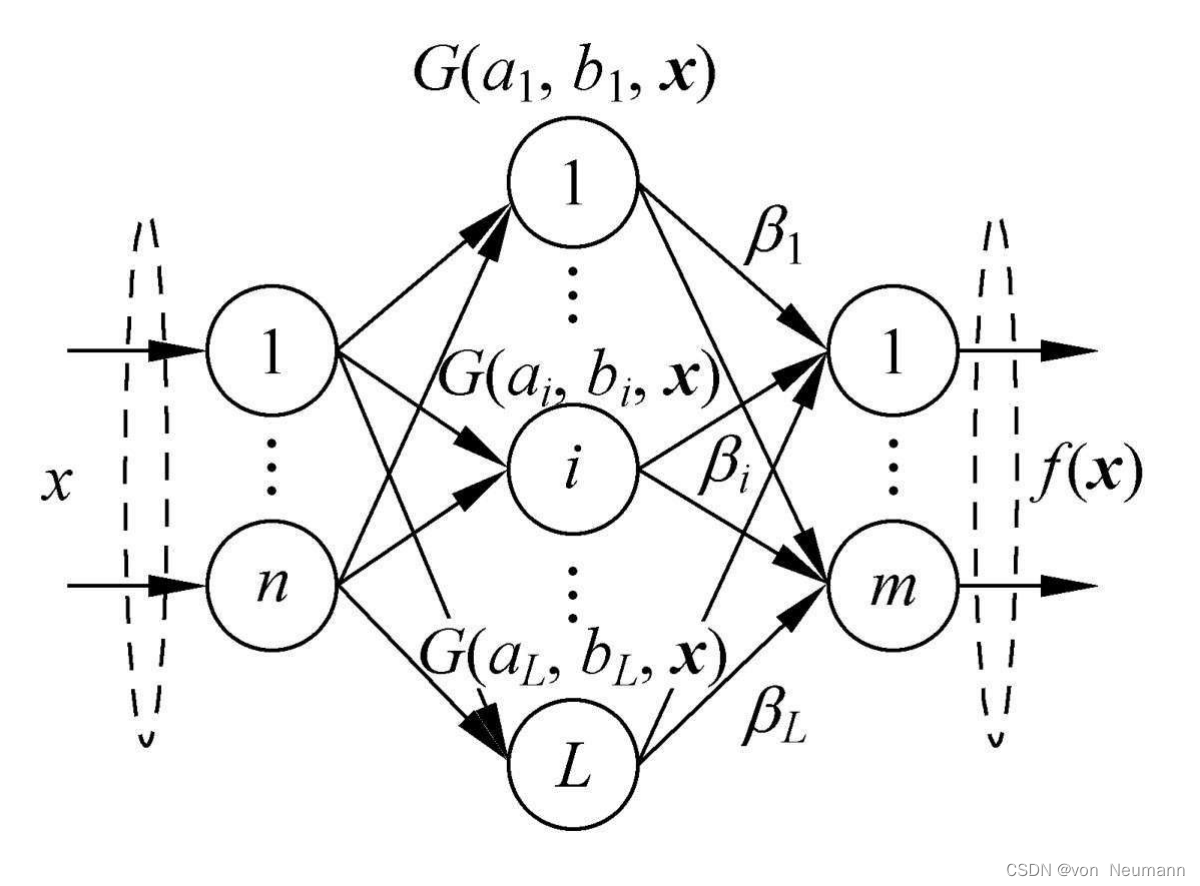
设训练集包括$N$个训练样本，将其表示为$(x_i,t_i)\in R^n\times R^m$，其中，$x_i$表示$n\times 1$维的输入向量，$t_i$表示第$i$个训练样本的期望输出向量，对于分类问题而言，$n$即代表训练样本的属性数，$m$则代表样本的类别数。如上图所示，若一个具有$L$个隐层节点的单隐层前馈神经网络能以零误差拟合上述$N$个训练样本，则意味着存在${\beta }_i,a_i,b_i$，使得下式成立：
$$f_L(x)=\sum _{i=1}^L{\beta }_{i}G(a_i,b_i,x_j)=t_j,k=1,2,\cdots ,N$$

其中，$a_i$和$b_i$分别表示第$i$个隐层节点的权重与偏置；${\beta }_i$表示第$i$个隐层节点的输出权重，即第$i$个隐层节点到各输出节点的连接权重；$G$表示激活函数，则上式可进一步简化为：
$$H\beta =T$$

其中：
$$H=\left[\begin{array}{ccc}G(a_1,b_1,x_1)& \cdots & G(a_L,b_L,x_1)\\ ⋮& \ddots & ⋮\\ G(a_1,b_1,x_N)& \cdots & G(a_N,b_N,x_N)\end{array}\right]$$

$$\beta =\left[\begin{array}{c}{\beta }_1^T\\ ⋮\\ {\beta }_L^T\end{array}\right]$$

$$T=\left[\begin{array}{c}{t}_1^T\\ ⋮\\ t_N^T\end{array}\right]$$

其中，$G(a_i,b_i,x_j)$表示第$j$个训练样本在第$i$个隐层节点上的激活函数值；$T$为所有训练样本对应的期望输出矩阵，通常将每个样本所对应类别输出节点的期望输出值设为$1$，其他节点的输出值则设为$-1$; $H$被称为隐层输出矩阵，其第$i$列为第$i$个隐层节点在所有训练样本上的输出向量，第$j$行为第$j$个训练样本在整个隐藏层中对应的输出向量。

在极限学习机中，由于所有$a_i$和KaTeX parse error: Expected group after '_' at position 3: bi_̲均是在$[-1,1]$区间内随机生成的，故输入样本、隐层权重与偏置、期望输出（类别标记）均已知，则输出权重矩阵$\beta$的近似解$\hat{\beta }$即可由下式直接计算得到：
$$\hat{\beta }=H^{T}T$$

其中，$H^T$为隐层输出矩阵的Moore-Penrose广义逆。根据其定义，可推知$\hat{\beta }$为该网络的最小范数最小二乘解。因此，极限学习机可通过进一步计算得到，而无须迭代训练，这就保证了神经网络的训练时间能被大幅缩减。同时，由于在求解过程中，约束了输出权重矩阵$\beta$的$L_2$范数，使其最小化，故可保证网络具有较强的泛化性能。

2012年，极限学习机的优化版本被提出，类似于支持向量机，其优化式可表示如下：
$$\begin{array}{rl}\min & L_{\text{ELM}}=\frac{1}{2}||\beta |{|}^2+\frac{1}{2}C\sum _{i=1}^N{ϵ}_I^2\\ \text{s.t.}& h(x_i)\beta =t_i-{ϵ}_i\end{array}$$

其中，${ϵ}_i$表示第$i$个训练样本的实际输出与期望输出之差；$h(x_i)$为第$i$个样例$x_i$在隐层上的输出向量，而$C$则为惩罚因子，用于调控网络的泛化性与精确性间的平衡关系。上述优化式可通过求解得到，给定一个具体的样本$x_i$，其对应的实际输出向量可由下式求得：
$$f(x)=\{\begin{array}{r}h(x)H^T(\frac{1}{C}+H{H}^T{)}^{-1}T,N<L\\ h(x)(\frac{1}{C}+H^{T}H{)}^{-1}{H}^{T}T,N\ge L\end{array}$$

其中，$f(x)=[f_1(x),f_2(x),\cdots ,f_m(x)]$则表示样本$x$的实际输出向量，并可进一步通过下式确定该样本的预测类标：
$$\text{Label}(x)=\arg \max f_i(x),i=1,2,\cdots ,m$$

下面考察样本类别不平衡分布对极限学习机会产生何种影响。从上面的理论分析可知，对于极限学习机而言，那些在属性空间中相邻较近的样本通常会有极其相似的输出值，而在类重叠区域，多数类样本会将少数类样本紧密地包裹其中，它们的输出值将极为接近。为同时保证所训练的极限学习机具有较强的泛化能力与较低的训练误差，少数类必然做出更多的牺牲。不失一般性，假设分类任务只有两个类别，其中在极限学习机中，少数类对应的期望输出为$1$，而多数类的期望输出为$-1$。考虑属性空间中两类样本的重叠区域，若可从该区域分割出一个足够小且样本分布致密的子区域，并保证在这一区域中多数类样例有$S$个，而少数类样例数恰好只有$1$个，即在此区域中，不平衡比率为$S$，则根据极限学习机的构造机理，这$S+1$个样例将有极其近似的输出值。设该少数类样本的特征向量为$x_0=(x_{01},x_{02},\cdots ,x_{0n})$，则$S$个多数类样例的特征向量可表示为：$x_i=(x_{01}+{\Delta }_{i1},x_{02}+{\Delta }_{i2},\cdots ,x_{0n}+{\Delta }_{in}),i=1,2,\cdots ,S$，其中，${\Delta }_{ij}$表示第$i$个多数类样例与少数类样例$x_0$相比，在第$j$个特征上的变化量，则在极限学习机训练完成后，这些样本的实际输出可表示为：
$$f(x_j)=\{\begin{array}{rl}& \sum _{i=1}^L{\beta }_{i}G(a_i,b_i,x_0),j=0\\ & \sum _{i=1}^L{\beta }_{i}G(a_i,b_i,x_0+\Delta x_j),j=1,2,\cdots ,S\end{array}$$

若以$\Delta f(x_j)$来表示第$j$个多数类样本对比少数类样本$x_0$在实际输出上的变化量，则其可表示如下：
$$\begin{array}{rl}\Delta f(x_j)& =\sum _{i=1}^L{\beta }_{i}G(a_i,b_i,x_0+\Delta x_j)-\sum _{i=1}^L{\beta }_{i}G(a_i,b_i,x_0)\\ & =\sum _{i=1}^L{\beta }_i(G(a_i,b_i,x_0+\Delta x_j)-G(a_i,b_i,x_0))\end{array}$$

若其中的激活函数$G$采用的是连续函数，且同时相邻样本在属性空间上的变化量$\Delta x_j$，隐层权重与偏置的$L_2$范数$||a||$、$||b||$，以及输出权重矩阵$||\beta ||$的$L_2$范数均足够小时，可保证两个邻近样本实际输出的变化量$\Delta f(x_j)$足够小。回顾上式，假定输出权重矩阵$\beta$已预先确定，则该致密区间的样例子集$Q_{\text{sub}}$的均方训练误差可表示为：
$$\begin{array}{rl}{Q}_{\text{sub}}& =(f(x_0)-1{)}^2+\sum _{i=1}^S(f(x_0)+\Delta f(x_i)-(1-){)}^2\\ & =f^2(x_0)-2f(x_0)+1+\sum _{i=1}^S(f^2(x_0)+2f(x_0)(\Delta f(x_i)+1)+\Delta f^2(x_i)+2\Delta f(x_i)+1)\end{array}$$

为最小化该子集的均方训练误差，可通过如下偏导式求解：
$$\frac{\partial Q_{\text{sub}}}{\partial f(x_0)}=(2S+2)f(x_0)+2\sum _{i=1}^S\Delta f(x_i)+2S-2=0$$

对上式进行求解，可得该子区间内的少数类样本的实际输出为：
$$f(x_0)=\frac{1-S-{\sum }_{i=1}^S\Delta f(x_i)}{S+1}$$

通过前面的分析可知${\sum }_{i=1}^S\Delta f(x_i)$足够小，故可忽略。此外，已知$S\gg 1$，则可推得该样本倾向于输出一个负值，且随着$S$的增大，该值越来越逼近多数类的期望输出值$-1$。通过上述推导分析，可得出如下结论：对于类别不平衡数据而言，在不同类的样本重叠区域，由于某类样本远远多于另一类，则样本相对较少的一类将会付出更大的错分代价。由此可知，类不平衡分布会对极限学习机的分类结果产生影响，且这种影响也是负面的。