吴恩达机器学习作业7（下）---Principal Component Analysis（包含实现，降维应用，可视化应用）

文章目录

implementing PCA

前言

PCA，即主成分分析，是流行的降维算法（无监督学习算法），其主要应用有

减小数据集的特征维度，从而减小内存或者磁盘储存的消耗
提升算法效率，加快算法的运行
将数据集的特征维度减小到3维及以下，方便可视化

代码分析

首先导入类库

import numpy as np
import matplotlib.pyplot as plt
import scipy.io #Used to load the OCTAVE *.mat files
from random import sample #Used for random initialization
import scipy.misc #Used to show matrix as an image
import matplotlib.cm as cm #Used to display images in a specific colormap
from scipy import linalg #Used for the "SVD" function
import imageio
from mpl_toolkits.mplot3d import Axes3D 

%matplotlib inline

导入数据并可视化

datafile = 'data/ex7data1.mat'
mat = scipy.io.loadmat( datafile )
X = mat['X']

#Quick plot
plt.figure(figsize=(7,5))
plot = plt.scatter(X[:,0], X[:,1], s=30, facecolors='none', edgecolors='b')
plt.title("Example Dataset",fontsize=18)
plt.grid(True)

在这里插入图片描述
下面开始编写PCA算法

数据集标准化函数

def featureNormalize(myX):
    means = np.mean(myX,axis=0)#对每列求均值
    myX_norm = myX - means
    stds  = np.std(myX_norm,axis=0)#对每列求标准差σ
    myX_norm = myX_norm / stds
    return means, stds, myX_norm

奇异值分解（SVD）函数，得到矩阵U，S，V

#SVD singular value decomposition
def getUSV(myX_norm):
    #求协方差矩阵
    cov_matrix = myX_norm.T.dot(myX_norm)/myX_norm.shape[0]
    # Run single value decomposition to get the U principal component matrix
    U, S, V = scipy.linalg.svd(cov_matrix, full_matrices = True, compute_uv = True)
    return U, S, V

好了，算法编写完毕

调用算法，得到参数

# Feature normalize
means, stds, X_norm = featureNormalize(X)
# Run SVD
U, S, V = getUSV(X_norm)

将principal component可视化

print('Top principal component is ',U[:,0])

#快速绘图，现在包括主成分
plt.figure(figsize=(7,5))
plot = plt.scatter(X[:,0], X[:,1], s=30, facecolors='none', edgecolors='b')
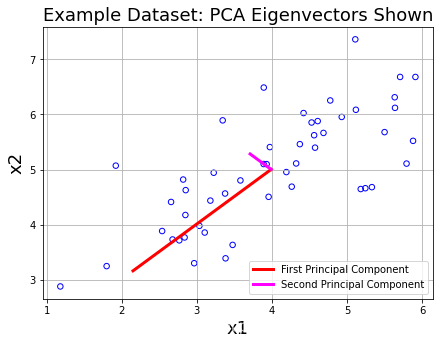
plt.title("Example Dataset: PCA Eigenvectors Shown",fontsize=18)
plt.xlabel('x1',fontsize=18)
plt.ylabel('x2',fontsize=18)
plt.grid(True)

#绘制主要组成部分
#means是数据集的中点，S的是主要成分的主要程度
plt.plot([means[0], means[0] + 1.5*S[0]*U[0,0]], 
         [means[1], means[1] + 1.5*S[0]*U[0,1]],
        color='red',linewidth=3,
        label='First Principal Component')
plt.plot([means[0], means[0] + 1.5*S[1]*U[1,0]], 
         [means[1], means[1] + 1.5*S[1]*U[1,1]],
        color='fuchsia',linewidth=3,
        label='Second Principal Component')

leg = plt.legend(loc=4)

如下图所示，红色的线段为最主要的component，洋红色的线段其次
在这里插入图片描述
下面调用算法，观察投影点情况

计算X在U_reduce上的投影点的向量

def projectData(myX, myU, K):
    Ureduced = myU[:,:K]
    z = myX.dot(Ureduced)
    return z

调用投影函数，得到一个二维样本点投影得到的一维坐标

#z为X在U_reduce上的投影点的向量（即投影点，一维）
z = projectData(X_norm,U,1)
print('Projection of the first example is %0.3f.'%float(z[0]))

Projection of the first example is 1.496.

下面进行原始数据的重构，即根据降维后的数据重构原始数据

重构函数

#原始数据的重构,返回 x_approx
#由于投影点z是一维的，不方便可视化，故转化为x_approx
def recoverData(myZ, myU, K):
    Ureduced = myU[:,:K]
    Xapprox = myZ.dot(Ureduced.T)  
    return Xapprox

测试

X_rec = recoverData(z,U,1)
print('Recovered approximation of the first example is ',X_rec[0])

Recovered approximation of the first example is [-1.05805279 -1.05805279]

得到了重构的二维原始数据

下面可视化投影过程

#Quick plot, now drawing projected points to the original points
plt.figure(figsize=(7,5))
#绘制原始散点图
plot = plt.scatter(X_norm[:,0], X_norm[:,1], s=30, facecolors='none', 
                   edgecolors='b',label='Original Data Points')
#绘制投影后的散点图
plot = plt.scatter(X_rec[:,0], X_rec[:,1], s=30, facecolors='none', 
                   edgecolors='r',label='PCA Reduced Data Points')

plt.title("Example Dataset: Reduced Dimension Points Shown",fontsize=14)
plt.xlabel('x1 [Feature Normalized]',fontsize=14)
plt.ylabel('x2 [Feature Normalized]',fontsize=14)
plt.grid(True)

for x in range(X_norm.shape[0]):
    #绘制样本点和投影点的连线
    plt.plot([X_norm[x][0],X_rec[x][0]],[X_norm[x][1],X_rec[x][1]],'k--')
    
leg = plt.legend(loc=4)

#Force square axes to make projections look better
dummy = plt.xlim((-2.5,2.5))
dummy = plt.ylim((-2.5,2.5))

在这里插入图片描述

Face Image Dataset

前言

代码分析

导入数据

datafile = 'data/ex7faces.mat'
mat = scipy.io.loadmat( datafile )
X = mat['X']

编写将numpy数组可视化的函数

#传入一张图片（1024，1）numpy数组，转化为（32，32）
def getDatumImg(row):
    width, height = 32, 32
    square = row.reshape(width,height)
    return square.T
    
#可视化数据
def displayData(myX, mynrows = 10, myncols = 10):
    width, height = 32, 32
    nrows, ncols = mynrows, myncols
    #大图片
    big_picture = np.zeros((height*nrows,width*ncols))
    
    irow, icol = 0, 0
    for idx in range(nrows*ncols):#每10张图片换行一次，遍历100张图片
        if icol == ncols:
            irow += 1
            icol  = 0
        iimg = getDatumImg(myX[idx])#读取图片的numpy数组（32，32）
        big_picture[irow*height:irow*height+iimg.shape[0],icol*width:icol*width+iimg.shape[1]] = iimg
        icol += 1
    fig = plt.figure(figsize=(10,10))
    plt.imshow(big_picture,cmap ='gray')

测试

displayData(X)

在这里插入图片描述
下面调用PCA算法对图片进行降维

# Feature normalize
means, stds, X_norm = featureNormalize(X)
# Run SVD
U, S, V = getUSV(X_norm)

得到矩阵U，由于矩阵U的每一个向量都是数据集的特征向量，注意到每个特征向量刚好满足（1024，1），与图片（32x32）格式相同，于是我们尝试可视化前36个principal component

# Visualize the top 36 eigenvectors found
#将前36个principal component可视化
displayData(U[:,:36].T,mynrows=6,myncols=6)

在这里插入图片描述
然后，我们再对图像进行降维，复原测试

1024维降到36维度

# Project each image down to 36 dimensions
#将每个图像投影到36维
#这里的k可以从1到1024（32x32）

#U中包含了所有特征向量，我们可以自行决定要降维到几维，只不过数据方差尽量维持在99%以上
z = projectData(X_norm, U, K=36)

36维度复原为图片

# Attempt to recover the original data
X_rec = recoverData(z, U, K=36)

可视化

# Plot the dimension-reduced data
displayData(X_rec)

在这里插入图片描述
1024维降到500维度

z = projectData(X_norm, U, K=500)

500维度复原为图片

X_rec = recoverData(z, U, K=500)

可视化

displayData(X_rec)

在这里插入图片描述
可见降维要选择合适的维度，保证数据方差 $\ge$ 99%

PCA for visualization

前言

在上次作业有一个图片压缩问题，采用K-means聚类算法，将成千上万种颜色聚类为16种，因为像素点为三维数据（red，green，bule），散落在三维RGB空间，我们当然可以将其可视化

但是三维空间的可视化较为臃肿，这里就可以用PCA算法将数据集降维到2维，从而轻松进行可视化了

代码分析

首先，我们先三维可视化样本点

subX = []
#遍历cluster，将样本点（像素）按颜色分类装入subX中
for x in range(len(np.unique(idxs))):
    subX.append(np.array([A[i] for i in range(A.shape[0]) if idxs[i] == x]))
    
fig = plt.figure()
ax = Axes3D(fig)   
#ax.legend(loc='best')
ax.set_zlabel('Z', fontdict={
    
    'size': 15, 'color': 'red'})
ax.set_ylabel('Y', fontdict={
    
    'size': 15, 'color': 'red'})
ax.set_xlabel('X', fontdict={
    
    'size': 15, 'color': 'red'})
    
for x in range(len(subX)):
    newX = subX[x]
    # 绘制散点图
    ax.scatter(newX[:,0], newX[:,1], newX[:,2])

在这里插入图片描述
然后我们运行PCA算法

# Feature normalize
#标准化特征
means, stds, A_norm = featureNormalize(A)
# Run SVD
U, S, V = getUSV(A_norm)

将x（三维）降维得到z（二维）

# Use PCA to go from 3->2 dimensions
z = projectData(A_norm,U,2)

下面进行二维可视化

# Make the 2D plot
subX = []
#遍历cluster，将样本点（像素）按颜色分类装入subX中
for x in range(len(np.unique(idxs))):
    subX.append(np.array([z[i] for i in range(A.shape[0]) if idxs[i] == x]))
        
fig = plt.figure(figsize=(8,8))
for x in range(len(subX)):
    newX = subX[x]
    plt.plot(newX[:,0],newX[:,1],'.',alpha=0.3)
    
plt.xlabel('z1',fontsize=14)
plt.ylabel('z2',fontsize=14)
plt.title('PCA Projection Plot',fontsize=16)
plt.grid(True)

在这里插入图片描述

PCA算法完美完成降维任务，~~实现了降维打击~~，实现了可视化

数据集

ex7data1.mat
ex7faces.mat
~~这里偷个懒，数据可以上kaggle查~~