【吴恩达课后编程作业】第二周作业 (附答案、代码) Logistic回归 神经网络、深度学习、机器学习
上一篇:【课程1 - 第二周作业】 ✌✌✌✌ 【目录】 ✌✌✌✌ 下一篇:【课程1 - 第三周作业】
首先说明一下,大学生一枚,最近在学习神经网络,写这篇文章只是记录自己的学习历程,起总结复习的作用,别无它意,本文参考了zsffuture的博客、布衣先生real的博客、孔小爽的博客、何宽的博客以及Github上fengdu78老师的文章进行学习
✌ 我们要实现一个能够识别猫的图片的简单神经网络
- numpy:常用数学工具库
- matplotlib:python的画图工具
- h5py:读取h5格式文件的工具
- lr_utils:用于加载训练及测试数据
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset
✌ 加载训练测试数据集
- x_train:训练集数据
- x_test:测试集数据
- y_train:训练集标签
- y_test:测试集标签
x_train,x_test,y_train,y_test,classes=load_dataset()
✌ 查看测试集的维度
这里的数据维度应为4维,例 [ 20 , 32 , 32 , 3]
第一维表示有多少张图片,2维和3维表示图片的宽和高,而第4维的3代表像素,RGB红绿蓝
这里就是有20张图片,每张的图片为的32*32的彩色图片,如果是1则为黑白照片
print(x_test.shape)
✌ 打印数据集的详细数据
print('训练集的数量:',x_train.shape[0])
print('测试集的数量:',x_test.shape[0])
print('训练集的数据维度:',x_train.shape)
print('测试集的数据维度:',x_test.shape)
print('训练集的标签维度:',y_train.shape)
print('测试集的标签维度:',y_test.shape)
print('图片的维度:',x_train[0].shape)
查看输出结果:
训练集的数量: 209
测试集的数量: 50
训练集的数据维度: (209, 64, 64, 3)
测试集的数据维度: (50, 64, 64, 3)
训练集的标签维度: (1, 209)
测试集的标签维度: (1, 50)
图片的维度: (64, 64, 3)
✌ 将图片数据向量化
上面说到测试集的图片维度为 (50, 64, 64, 3),我们要将每个像素点提取出来作为1个特征,说白了就是将图片拉长,变成50行,64643列的矩阵
那么为什么要将其转置呢,正常来说不是行数代表样本量,列数代表特征数吗?
这是因为后面构建神经网络时,涉及到矩阵的运算,转置后计算会更方便一些,看到后面你就会get到这个点
x_train=x_train.reshape(x_train.shape[0],-1).T
x_test=x_test.reshape(x_test.shape[0],-1).T
✌ 打印向量化后的数据维度
print(x_train.shape)
print(x_test.shape)
查看输出结果:
(12288, 209)
(12288, 50)
✌ 向量归一化
在传统机器学习中,我们在将数据导入模型训练之前首先要将数据归一化,转化到0~1之间,为了消除量纲的影响和有利于模型的计算
而在图片也需要这点,但图片的处理方式会更容易一些,因为图片的每个像素是0~255之间的数字组成,所以我们只需要将该图片矩阵除255即可,就会将矩阵缩放到0-1之间
x_train=x_train/255
x_test=x_test/255
x_train[0,0:10]
查看第一张图片的前10个特征:
array([2.61437908e-04, 3.01422530e-03, 1.26105344e-03, 1.53787005e-05,
1.38408304e-04, 1.29181084e-03, 8.61207228e-04, 2.92195309e-04,
9.68858131e-04, 3.53710111e-04])
✌ 神经网络介绍
现在我们的准备工作已经做好了,接下来就是搭建神经网络
z = w . T ∗ X + b z=w.T*X+b z=w.T∗X+b
y = a = s i g m o i d ( z ) y=a=sigmoid(z) y=a=sigmoid(z)
单一样本的损失:
L ( y , a ) = − ( y ∗ l o g ( a ) + ( 1 − y ) ∗ l o g ( 1 − a ) ) L(y,a)=-(y*log(a)+(1-y)*log(1-a)) L(y,a)=−(y∗log(a)+(1−y)∗log(1−a))
计算所有样本的平均损失值:
J = 1 / m ∑ i = 0 m L ( y , a ) J=1/m\sum_{i=0}^mL(y,a) J=1/mi=0∑mL(y,a)
搭建神经网络的主要步骤是:
-
定义模型结构(例如输入特征的数量)
-
初始化模型的参数
扫描二维码关注公众号,回复: 12808284 查看本文章
-
不断迭代(调整参数):
3.1 计算当前损失(正向传播)
3.2 计算当前梯度(反向传播)
3.3 更新参数(梯度下降)
✌ 定义sigmoid函数
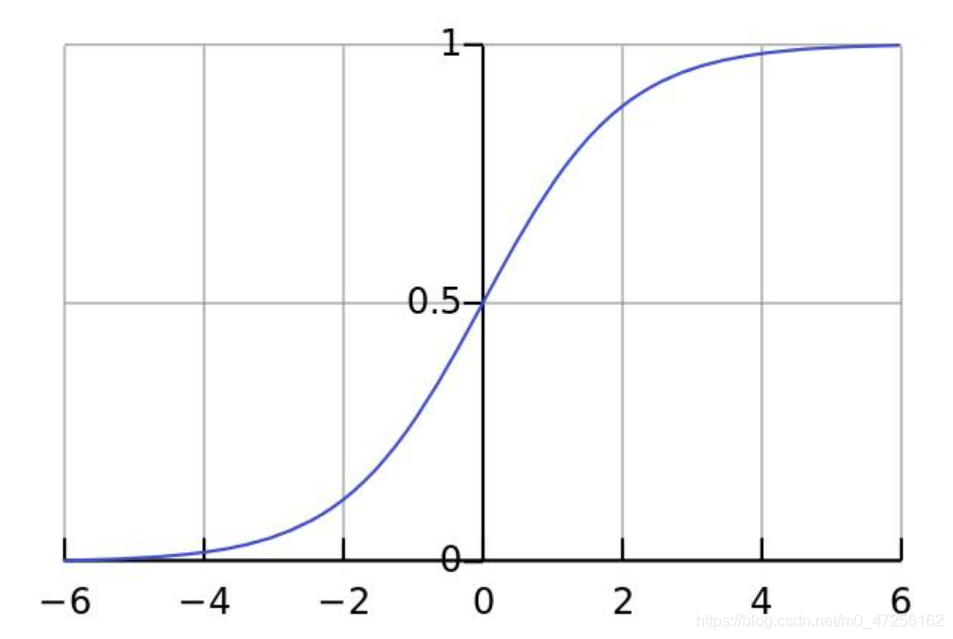
a = s i g m o i d ( z ) a=sigmoid(z) a=sigmoid(z)
s i g m o i d = 1 / ( 1 + e − x ) sigmoid=1/(1+e^-x) sigmoid=1/(1+e−x)
因为我们要做的是二分类问题,所以到最后要将其转化为概率,所以可以利用sigmoid函数的性质将其转化为0~1之间
def sigmoid(z):
"""
功能:激活函数,计算sigmoid的值
参数:
z - 任何维度的矩阵
返回:
s - sigmoid(z)
"""
s=1/(1+np.exp(-z))
return s
✌ 定义初始化w、b的函数
在进行梯度下降之前,要初始化w和b的值,我们为了简单都将其初始化为0
w的维度应为(特征数,1)
这里就验证了之前说到的特征转置
z = w . T ∗ X + b z=w.T*X+b z=w.T∗X+b
可以看到刚好对应矩阵的维度
b为一常数
def init_w_b(dim):
"""
功能:初始化w,b的维度和值
参数:
dim - w要初始化的行维度,就是特征数
返回:
w - 初始化好的(dim,1)维矩阵
b - 常数0
"""
# 将w初始化为列矩阵
w=np.zeros((dim,1))
b=0
return w,b
✌ 定义传播函数
神经网络分为正向传播和反向传播
正向传播计算求出损失函数,然后反向计算各个梯度
然后进行梯度下降,更新参数
def propagate(w,b,X,Y):
"""
功能:正向传播和反向传播
计算损失函数,以及各权重w,偏置b的梯度
参数:
w - 初始化好的权重矩阵(特征数,1)维
b - 偏置b
X - 训练数据 (特征数,样本数)维
Y - 训练标签 (1,样本数)维
返回:
grads - 各权重和偏置的梯度
loss - 损失值
"""
# m:为样本数
m=X.shape[1]
# 正向传播计算损失
a=sigmoid(np.dot(w.T,X)+b)
loss=(-1/m)*np.sum(Y*np.log(a)+(1-Y)*np.log(1-a))
# 反向传播计算梯度
dw=(1/m)*np.dot(X,(a-Y).T)
db=(1/m)*np.sum(a-Y)
grads={
'dw':dw,'db':db}
return grads,loss
✌ 定义优化器函数
目标是通过最小化损失函数 J来学习 w 和 b 。对于参数 λ,更新规则是 w = w − λ ∗ d J / d w w=w-λ*dJ/dw w=w−λ∗dJ/dw b = b − λ ∗ d J / d b b=b-λ*dJ/db b=b−λ∗dJ/db,其中 λ 是学习率。
num_iter代表梯度下降时的迭代次数,就是w的改变次数,求取损失函数的最小值,即全局最优解,这里可能会产生局部最优解,会影响模型结果,这里不与阐述,可以选择其他较好的优化器
大多数优化器都是基于梯度下降这种方法,只不过具体的数学计算有些不同
def optimizer(w,b,X,Y,num_iter,lr,print_loss=False):
"""
功能:优化函数,进行梯度下降,不断更新权重值,求取最优解
参数:
w - 初始化好的权重矩阵(特征数,1)维
b - 偏置b
X - 训练数据 (特征数,样本数)维
Y - 训练标签 (1,样本数)维
num_iter - 梯度下降时的迭代次数
lr - 学习率 w=w-lr*dw
print_loss - 是否每100次迭代打印一次缺失值
返回:
params - 训练好后的w和b值
grads - 各权重和偏置的梯度
loss - 各迭代次数下的损失值
"""
# 不同迭代次数下的损失值
losses=[]
# 进行迭代
for i in range(num_iter):
# 开始传播,计算梯度
grads,loss=propagate(w,b,X,Y)
dw=grads['dw']
db=grads['db']
# 更新参数,梯度下降
w=w-lr*dw
b=b-lr*db
if i%100==0:
losses.append(loss)
if print_loss and i%100==0:
print('迭代次数:%d,误差值:%f'%(i+1,loss))
params={
'w':w,'b':b}
grads={
'dw':dw,'db':db}
return params,grads,losses
✌ 定义预测函数
上面optimizer函数会输出已经训练好的w、b参数,我们可以利用它们进行预测新的样本集
进行预测两个步骤:
- y = a = s i g m o i d ( w . T ∗ X + b ) y=a=sigmoid(w.T*X+b) y=a=sigmoid(w.T∗X+b)
- 利用概率将其转化为0-1类别
- 将结果存储到y_pred中
def predict(w,b,X):
"""
功能:利用优化好的w和b值进行预测
参数:
w - 初始化好的权重矩阵(特征数,1)维
b - 偏置b
X - 训练数据 (特征数,样本数)维
返回:
y_pred - 预测值(1,样本数)维
"""
# 样本数
m=X.shape[1]
# 将y_pred变成和标签同维度的举证
y_pred=np.zeros((1,m))
# 激活
a=sigmoid(np.dot(w.T,X)+b)
# 根据概率进行二分类判断
for i in range(m):
y_pred[0,i]=1 if a[0,i]>0.5 else 0
return y_pred
✌ 定义模型函数
我们已经将所需要的所有函数已经封装好了,现在需要一个训练函数调用它们,完成模型的训练,model的作用就是如此
def model(x_train,x_test,y_train,y_test,num_iter,lr,print_loss=False):
"""
功能:利用前面封装好的函数进行训练
参数:
x_train - 训练数据(特征数,样本数)
x_test - 初始化好的权重矩阵(特征数,样本数)
y_train - 初始化好的权重矩阵(1,样本数)
y_test - 初始化好的权重矩阵(1,样本数)
num_iter - 梯度下降的迭代次数
lr - 学习率
print_loss - 是否每100次打印loss值
返回:
d - 预测结果以w,b等数据
"""
# 初始化参数w、b
w,b=init_w_b(x_train.shape[0])
# 开始梯度下降
params,grads,losses=optimizer(w,b,x_train,y_train,num_iter,lr,print_loss)
w,b=params['w'],params['b']
# 预测训练集和测试集
y_pred_train=predict(w,b,x_train)
y_pred_test=predict(w,b,x_test)
# 计算准确率
print('训练集的准确性:%.3f'%((y_pred_train==y_train).sum()/y_train.shape[1]*100),'%')
print('测试集的准确性:%.3f'%((y_pred_test==y_test).sum()/y_test.shape[1]*100),'%')
d = {
"losses" : losses,
"y_pred_train" : y_pred_train,
"y_pred_test" : y_pred_test,
"w" : w,
"b" : b,
"learning_rate" :lr,
"num_iter" : num_iter }
return d
✌ 进行测试
我们将我们处理好的训练测试集传入,测试下模型的效果,并每迭代100次打印下损失函数的值,观察模型效果是否得到了优化
print("====================测试model====================")
d = model(x_train,x_test,y_train,y_test,2000,0.003,True)
查看输出结果:
====================测试model====================
迭代次数:1,误差值:0.693147
迭代次数:101,误差值:0.686231
迭代次数:201,误差值:0.680305
迭代次数:301,误差值:0.675226
迭代次数:401,误差值:0.670873
迭代次数:501,误差值:0.667139
迭代次数:601,误差值:0.663935
迭代次数:701,误差值:0.661184
迭代次数:801,误差值:0.658821
迭代次数:901,误差值:0.656790
迭代次数:1001,误差值:0.655043
迭代次数:1101,误差值:0.653539
迭代次数:1201,误差值:0.652244
迭代次数:1301,误差值:0.651129
迭代次数:1401,误差值:0.650167
迭代次数:1501,误差值:0.649337
迭代次数:1601,误差值:0.648620
迭代次数:1701,误差值:0.648002
迭代次数:1801,误差值:0.647467
迭代次数:1901,误差值:0.647004
训练集的准确性:65.550 %
测试集的准确性:34.000 %
✌ 画学习曲线

这里我们可以看到随着迭代次数的增加,模型的损失函数越来越小,这都是梯度下降所起到的作用,说明我们的w、b等值更新的正确,朝着全局最优解的方向进行
losses=d['losses']
# 横坐标为迭代次数*100 ,纵坐标为损失值
plt.plot(range(1,len(losses)+1),losses)
plt.title('l r=0.003')
plt.xlabel('iters(*100)')
plt.ylabel('losses')
plt.show()
✌ 学习率曲线
上面我们看到当学习率为0.03时模型效果并不是很好,可能是梯度下降时影响了参数的变化速率及值的变化,所以我们可以画学习曲线去观察不同学习率的模型评估效果

lr=[0.01,0.001,0.0001,0.00001]
models={
}
for i in lr:
print('learning rate is :',i)
models[str(i)]=model(x_train,x_test,y_train,y_test,2000,i)
print('\n'+"----------------------------------------")
for i in lr:
plt.plot(range(1,len(models[str(i)]['losses'])+1),models[str(i)]['losses'],label=str(i))
plt.xlabel('iter(*100)')
plt.ylabel('losses')
plt.legend(loc='upper right')
plt.show()
查看输出结果:
learning rate is : 0.01
训练集的准确性:99.522 %
测试集的准确性:70.000 %
----------------------------------------
learning rate is : 0.001
训练集的准确性:91.388 %
测试集的准确性:68.000 %
----------------------------------------
learning rate is : 0.0001
训练集的准确性:71.292 %
测试集的准确性:40.000 %
----------------------------------------
learning rate is : 1e-05
训练集的准确性:65.550 %
测试集的准确性:34.000 %
----------------------------------------