最短路径:C Apare_xzc
2010年上海交通大学计算机研究生机试真题
2020/3/21
题目链接:codeup contest 100000621C题 <–
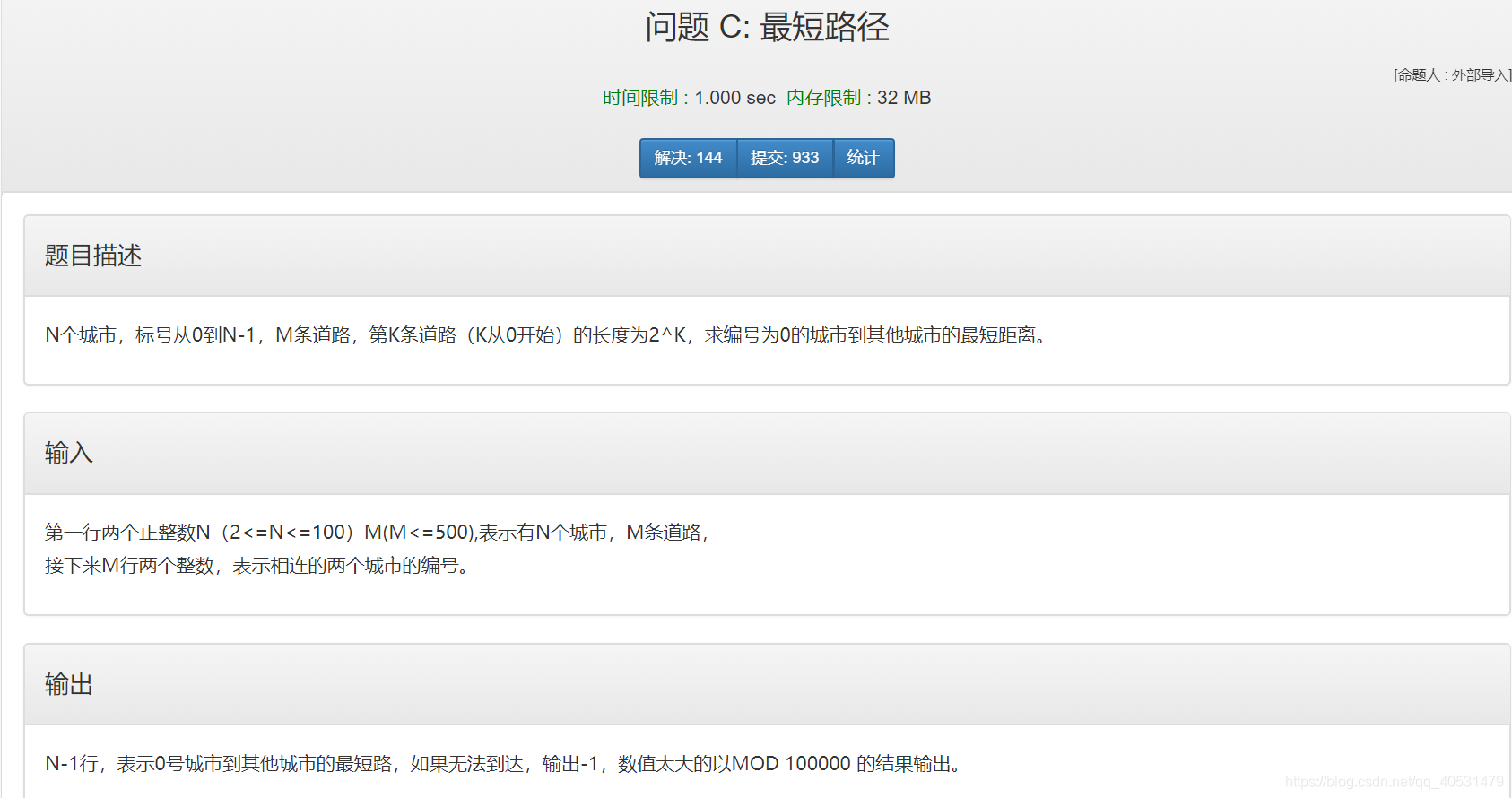
据说多组输入,有重边
样例输入1:
4 3
0 1
1 2
2 0
样例输出1:
1
3
-1
样例输入2:
4 4
1 2
2 3
1 3
0 1
样例输出2:
8
9
11
分析:
这显然是求单源最短路。我们第一反应就是Dijkstra。其实这道题的节点个数才100,O(n^3)的Floyd算法也可以。但是这道题与众不同的地方,就是它的边权都是2^k,这些边我们无法用long long存储。 我们要充分挖掘题目的特殊性。
我们可以知道,边长指数型增长非常之快。2^k > 2^0 + 2^1 + 2^2 + 2^3 + ... + 2^(k-1))。由于输入的第K条边的长度为2^K,所以后面的边比前面所有边之和还要大。换句话说,如果前面两点已经连同,那么我们没有必要用后面的边去更新最短路。
解法一:写一个二进制大数类,然后开心地跑Dijkstra。
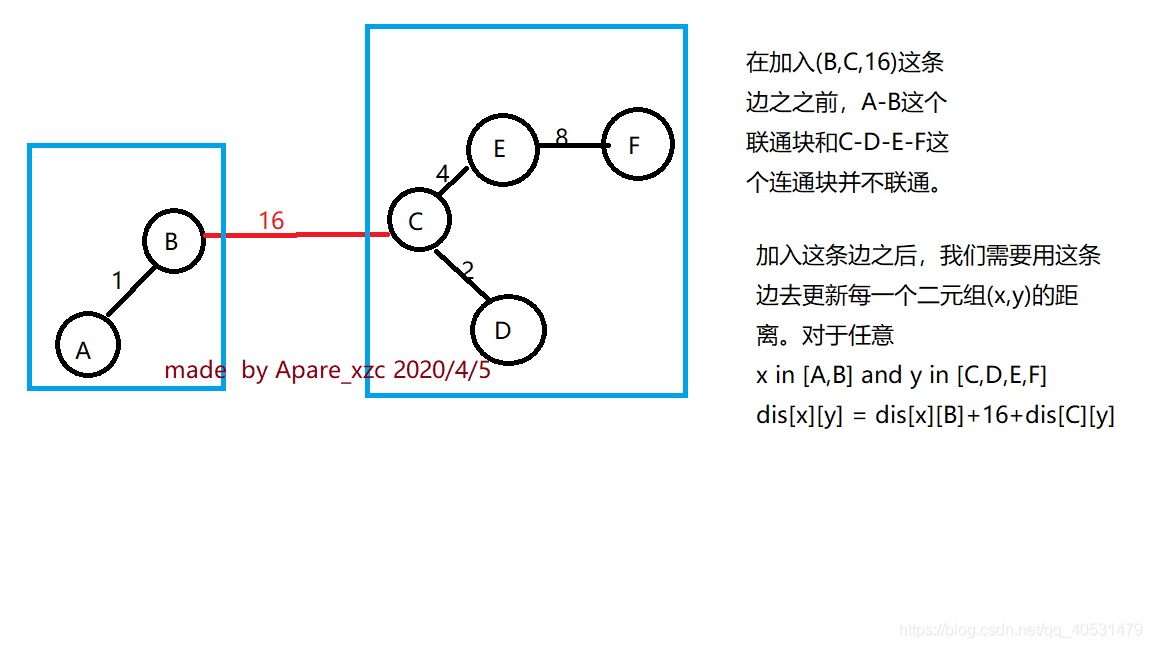
解法二:由刚才的分析可得,出现在前面的边,只要能使两点连通,那么这两点见的最短距离就定下来了。我们每次得到的边(x,y,d),如果x,y已经联通,那么这条边没有意义,因为它比之前所有的边之和都大,我们舍弃掉。如果x,y没有联通,就用这条长为d的边,去计算两个连通块之间两两结点的距离。对于任意X in [x, …] and Y in [y, …] dis[x][y] = dis[X][x] + d + dis[y][Y]
代码一:
二进制大数类+Dijkstra 27ms
O(mlogm * m)
#include <bits/stdc++.h>
using namespace std;
const int mod = 100000;
struct BigNum {
int s[504],h;
int toInt() {
if(h==502) return -1;
int ans = 0;
for(int i=h; i>=0; --i) ans = (ans*2+s[i])%mod;
return ans;
}
BigNum operator = (const BigNum& rhs) {
h = rhs.h;
for(int i=0; i<504; ++i) s[i] = rhs.s[i];
return *this;
}
BigNum(int k) {
memset(s,0,sizeof(s));
h = k; s[k] = 1;
}
BigNum() {
memset(s,0,sizeof(s));
h = 0;
}
bool operator < (const BigNum& rhs)const {
if(h!=rhs.h) return h<rhs.h;
for(int i=h-1; i>=0; --i) {
if(s[i]>rhs.s[i]) return false;
else if(s[i]<rhs.s[i]) return true;
}
return false;
}
bool operator > (const BigNum& rhs)const {
if(h!=rhs.h) return h>rhs.h;
for(int i=h-1; i>=0; --i) {
if(s[i]>rhs.s[i]) return true;
else if(s[i]<rhs.s[i]) return false;
}
return false;
}
friend BigNum operator + (const BigNum& a,const BigNum& b) {
BigNum res;
int H = max(a.h,b.h);
for(int i=0; i<=H; ++i) {
res.s[i] += a.s[i]+b.s[i];
res.s[i+1] = res.s[i]/2;
res.s[i] %= 2;
}
if(res.s[H+1]!=0) res.h = H+1;
else res.h = H;
return res;
}
};
struct Node {
int to,Next;
BigNum d;
} node[1005];
int head[102],tot;
void initEdge(int n) {
tot = 0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int k) {
node[tot].to = v;
node[tot].d = BigNum(k);
node[tot].Next = head[u];
head[u] = tot++;
}
struct A {
int id;
BigNum dd;
bool operator < (const A& rhs)const {
return dd > rhs.dd;
} A() {}
A(int i,BigNum ddd) {
id = i; dd = ddd;
}
}An;
BigNum dis[101];
bool vis[101];
void Dijkstra(int n) {
for(int i=1; i<n; ++i) dis[i] = BigNum(502);
memset(vis,false,sizeof(vis));
priority_queue<A> Q;
Q.push(A(0,BigNum()));
int u = 0;
BigNum dd;
while(!Q.empty()) {
An = Q.top(); Q.pop();
u = An.id; dd = An.dd;
vis[u] = true;
for(int i=head[u]; i!=-1; i=node[i].Next) {
int to = node[i].to;
if(vis[to]) continue;
BigNum nd = node[i].d+dd;
if(nd<dis[to]) {
dis[to] = nd;
Q.push(A(to,dis[to]));
}
}
}
for(int i=1; i<n; ++i)
printf("%d\n",dis[i].toInt());
}
int main(void) {
int n,m,x,y;
while(cin>>n>>m) {
int k = 0;
initEdge(n);
while(m--) {
scanf("%d%d",&x,&y);
addedge(x,y,k);addedge(y,x,k++);
}
Dijkstra(n);
}
return 0;
}
代码二:
Folyd:O(m*n^2)
#include <bits/stdc++.h>
using namespace std;
const int N = 101;
const int mod = 100000;
int dis[N][N];
int main(void) {
int n,m,x,y;
freopen("1.in","r",stdin);
while(cin>>n>>m) {
memset(dis,-1,sizeof(dis)); //初始化为均不连通
for(int i=0;i<n;++i) dis[i][i] = 0; //自己和自己联通,便于后续更新
int d = 1;
while(m--) {
scanf("%d%d",&x,&y);
if(dis[x][y]!=-1) { //若x,y已经联通,则没有必要更新
d = (d<<1)%mod;
continue;
}
for(int i=0;i<n;++i) {
if(dis[x][i]==-1) continue;
for(int j=0;j<n;++j) { //i和x联通,j和y联通
if(dis[y][j]!=-1&&dis[i][j]==-1) //且i和j不连通
dis[i][j]=dis[j][i]=(dis[x][i]+dis[y][j]+d)%mod;
}
}
dis[x][y] = dis[y][x] = d;
d = (d<<1)%mod;
}
for(int i=1;i<n;++i)
printf("%d\n",dis[0][i]);
}
return 0;
}
xzc
2020/3/21 20:24