《恋上数据结构第1季》二叉树基础、真二叉树、满二叉树、完全二叉树、二叉树的遍历（重点）

数据结构与算法笔记目录：《恋上数据结构》 笔记目录

想加深 Java 基础推荐看这个： Java 强化笔记目录

如果你想看的是二叉树的代码实现，请看这个：二叉树代码实现

简单的看一下树形结构：

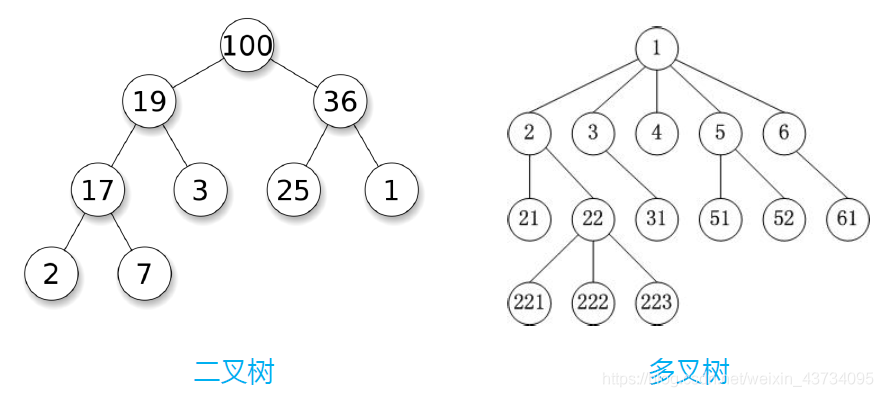
生活中的树形结构：

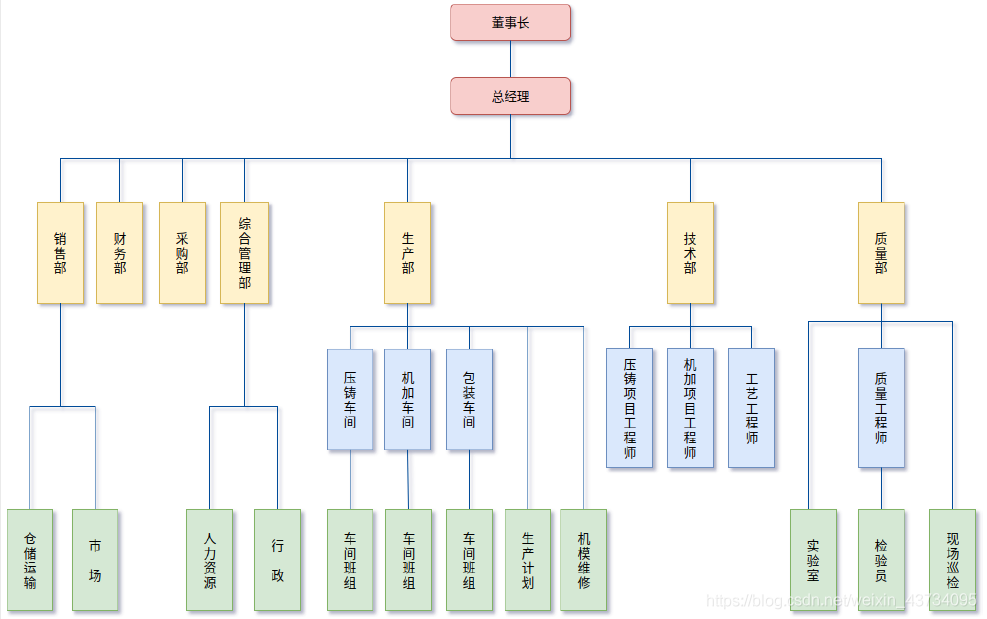
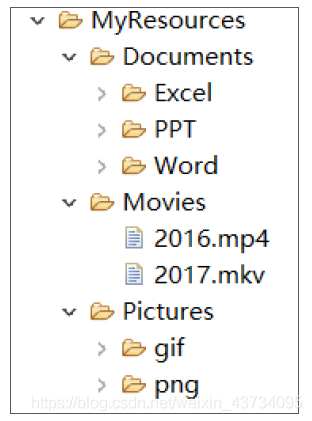
• 使用树形结构可以大大提高效率；
• 树形结构是算法面试的重点；

树（Tree）的基本概念

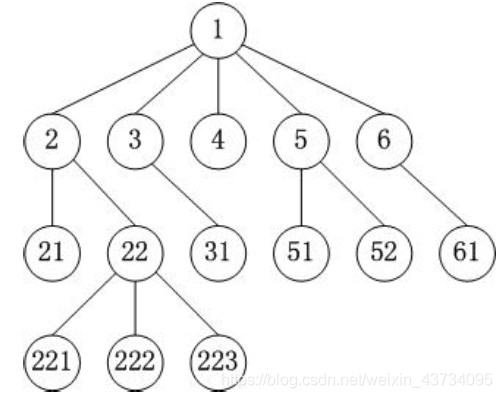
节点、根节点、父节点、子节点、兄弟节点；

• 一棵树可以没有任何节点，称为空树
• 一棵树可以只有 1 个节点，也就是只有根节点

子树、左子树、右子树；

节点的度（degree）：子树的个数；

树的度：所有节点度中的最大值；

叶子节点（leaf）：度为 0 的节点；

非叶子节点：度不为 0 的节点；

层数（level）：根节点在第 1 层，根节点的子节点在第 2 层，以此类推（有些教程也从第 0 层开始计算）

节点的深度（depth）：从根节点到当前节点的唯一路径上的节点总数；

节点的高度（height）：从当前节点到最远叶子节点的路径上的节点总数；

树的深度：所有节点深度中的最大值；
树的高度：所有节点高度中的最大值；
数的深度 等于 树的高度；

有序树、无序树、森林

有序树：树中任意节点的子节点之间有顺序关系；

无序树：树中任意节点的子节点之间没有顺序关系，也称为 “自由树”；

森林：由 m（m ≥ 0）棵互不相交的树组成的集合；

二叉树（Binary Tree）

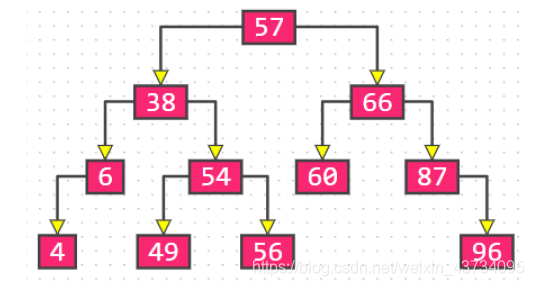
二叉树的特点：

• 每个节点的度最大为 2（最多拥有 2 棵子树）
• 左子树和右子树是有顺序的，二叉树是有序树
• 即使某节点只有一棵子树，也要区分左右子树
  

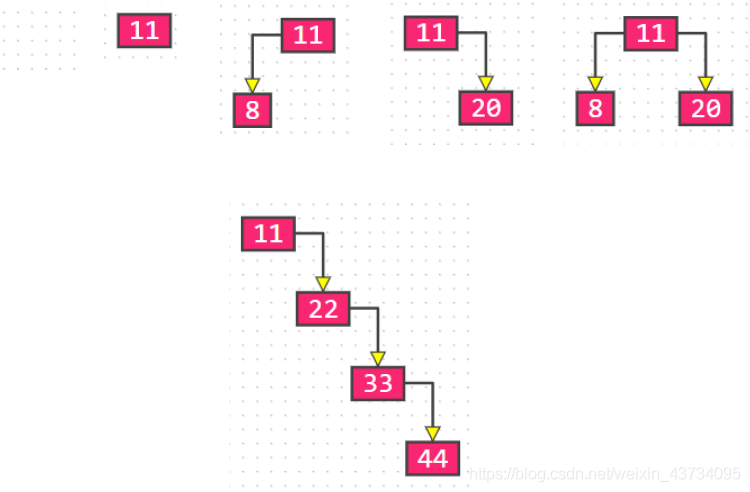
二叉树的性质

非空二叉树的第 i 层，最多有 2ⁱ⁻¹ 个节点（ i ≥ 1 ）

在高度为 h 的二叉树上最多有 2^h-1 个结点（ h ≥ 1 ）

对于任何一棵非空二叉树，如果叶子节点个数为 n0，度为 2 的节点个数为 n2，则有：n0 = n2 + 1

• 假设度为 1 的节点个数为 n1，那么二叉树的节点总数 n = n0 + n1 + n2
• 二叉树的边数 T = n1 + 2 * n2 = n – 1 = n0 + n1 + n2 – 1
• 因此 n0 = n2 + 1

真二叉树（Proper Binary Tree）

真二叉树：所有节点的度都要么为 0，要么为 2

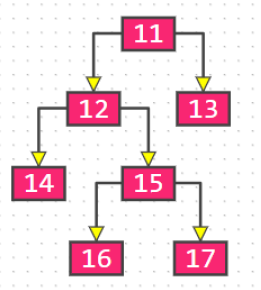
下图不是真二叉树：

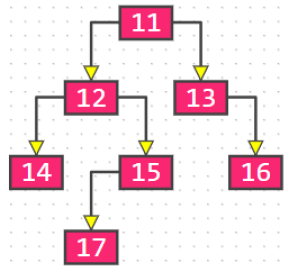
满二叉树（Full Binary Tree）

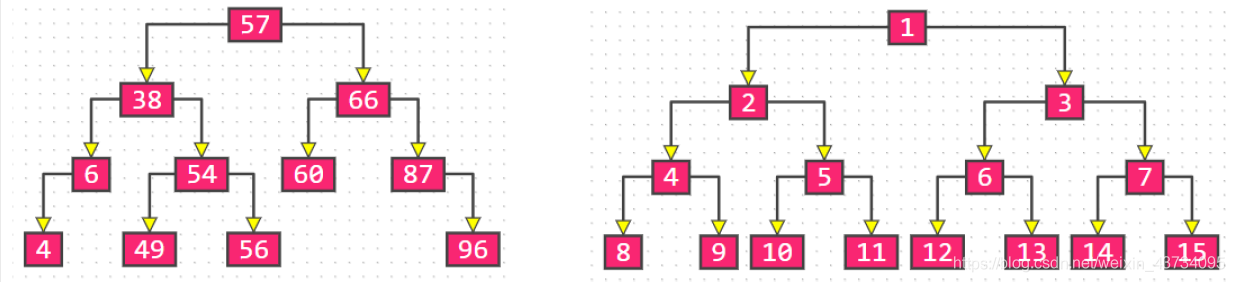
满二叉树：最后一层节点的度都为 0，其他节点的度都为 2

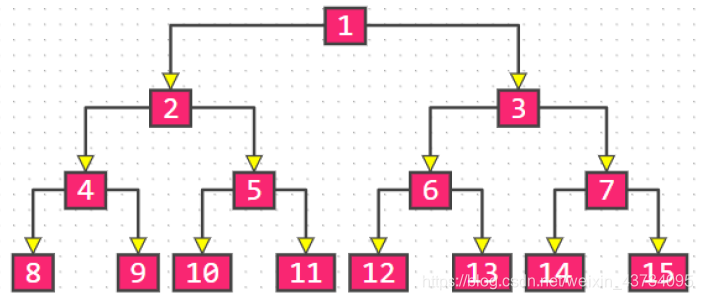
假设满二叉树的高度为 h（ h ≥ 1 ），那么

• 第 i 层的节点数量： 2ⁱ⁻¹
• 叶子节点数量： 2^h−1
• 总节点数量 n
  • n = 2^h − 1 = 2⁰ + 2¹ + 2² + ⋯ + 2^h−1
• 树高度与总节点的关系：h = log₂(n + 1)

在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多；
满二叉树一定是真二叉树，真二叉树不一定是满二叉树；

完全二叉树（Complete Binary Tree）

完全二叉树：对节点从上至下、左至右开始编号，其所有编号都能与相同高度的满二叉树中的编号对应

完全二叉树的性质

• 度为 1 的节点只有左子树
• 度为 1 的节点要么是 1 个，要么是 0 个
• 同样节点数量的二叉树，完全二叉树的高度最小
• 假设完全二叉树的高度为 h（ h ≥ 1 ），那么：
  • 至少有 2^h−1 个节点 （ 2⁰ + 2¹ + 2² + ⋯ + 2^h−2 + 1 ）
  • 最多有 2^h − 1 个节点（ 2⁰ + 2¹ + 2² + ⋯ + 2^h−1，即 满二叉树 ）
  • 总节点数量为 n
    2^h−1 ≤ n < 2^h
    h − 1 ≤ log₂n < h
    h = floor( log₂n ) + 1
    （ floor 是向下取整，ceiling 是向上取整 ）

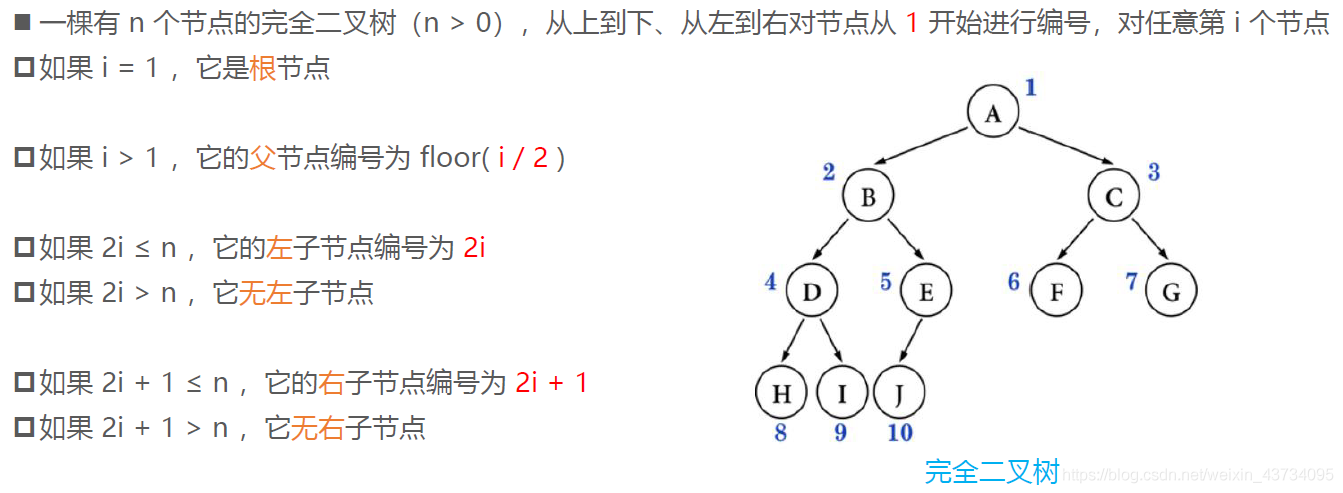
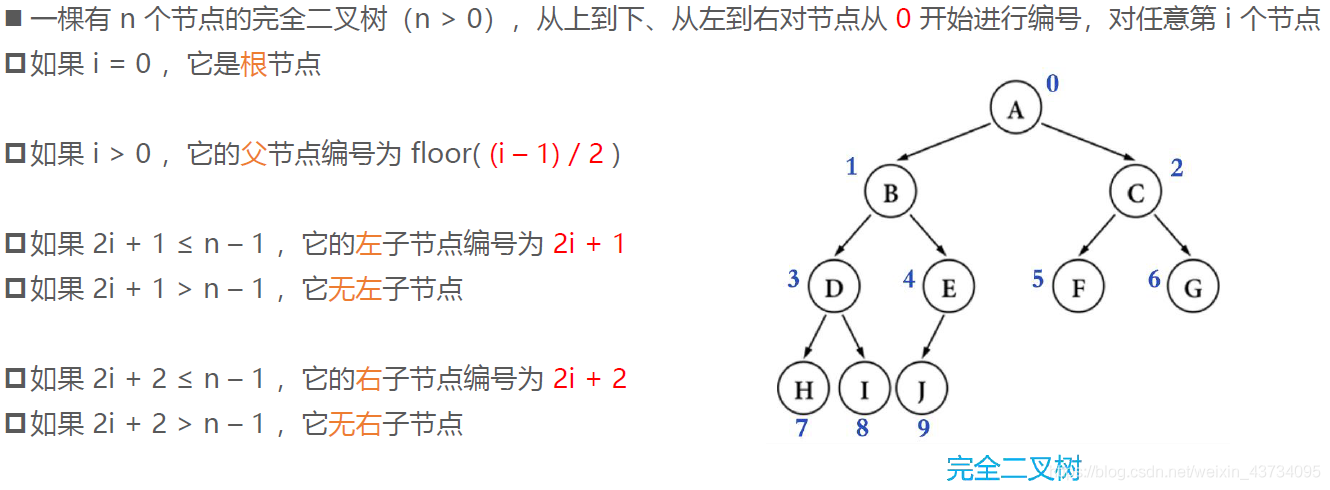
下图不是完全二叉树：

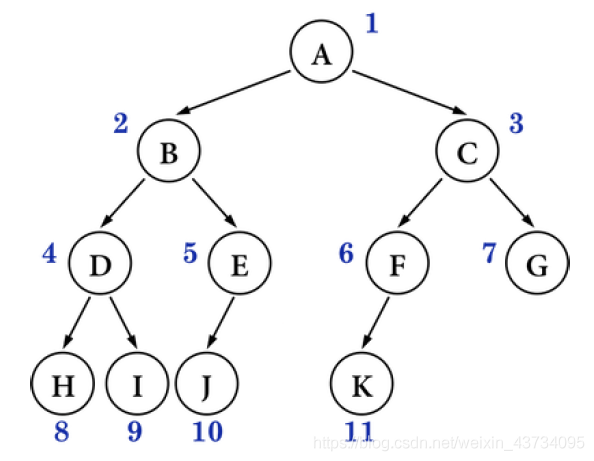
面试题（完全二叉树）

国外教材的说法：了解一下

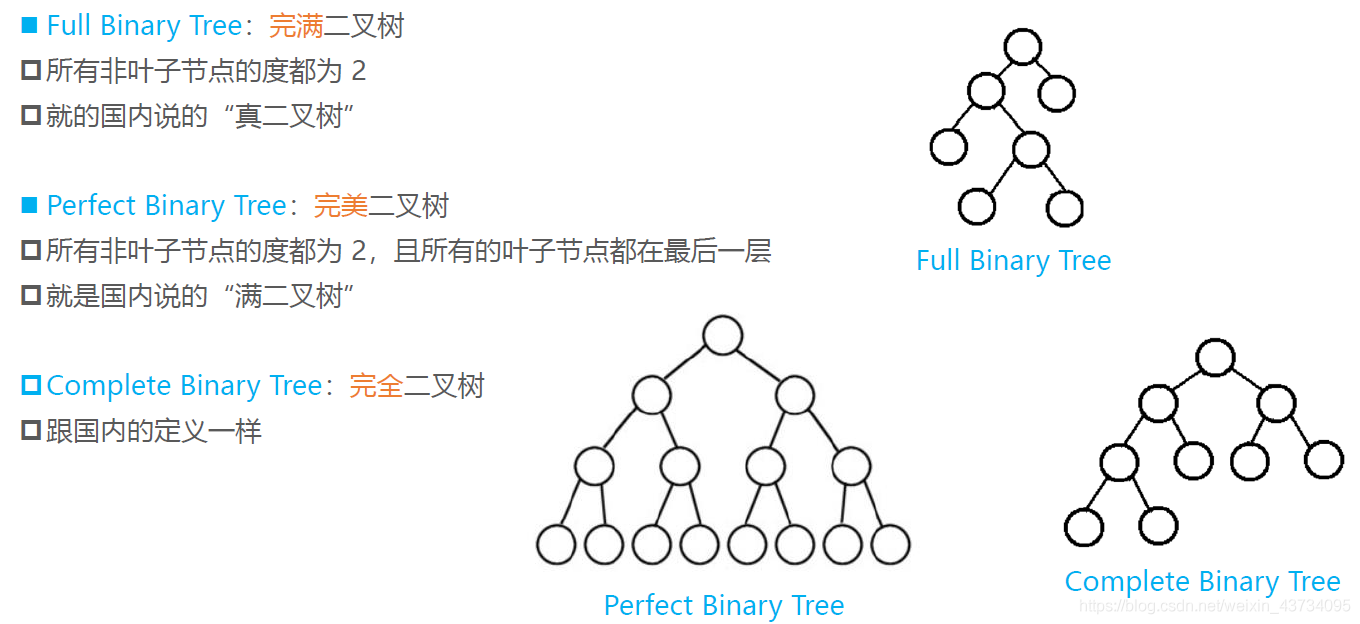
二叉树的遍历 + 练习题

遍历是数据结构中的常见操作：把所有元素都访问一遍；

线性数据结构的遍历比较简单：

• 正序遍历
• 逆序遍历

根据节点访问顺序的不同，二叉树的常见遍历方式有 4 种：

• 前序遍历（Preorder Traversal）
• 中序遍历（Inorder Traversal）
• 后序遍历（Postorder Traversal）
• 层序遍历（Level Order Traversal）

遍历的应用：

• 前序遍历：树状结构展示（注意左右子树的顺序）
• 中序遍历：二叉搜索树的中序遍历按升序或者降序处理节点
• 后序遍历：适用于一些先子后父的操作
• 层序遍历：计算二叉树的高度、判断一棵树是否为完全二叉树

前序遍历（Preorder Traversal）

访问顺序：根节点、前序遍历左子树、前序遍历右子树

下图前序遍历的结果是：7、4、2、1、3、5、9、8、11、10、12

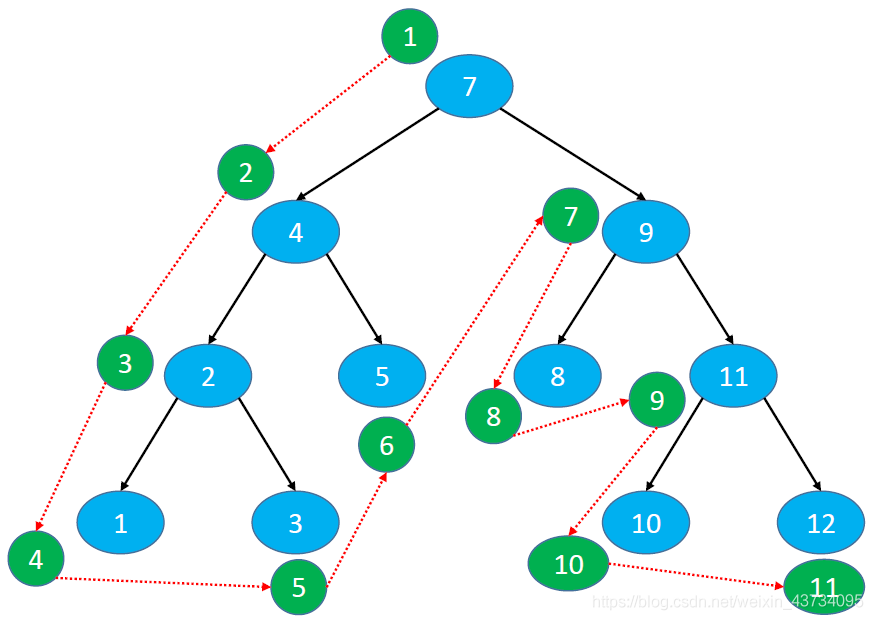
二叉树的前序遍历：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
	List<Integer> list = new ArrayList<>();
	public List<Integer> preorderTraversal(TreeNode root) {
        if(root == null) return list;
        
        list.add(root.val);
        preorderTraversal(root.left);
        preorderTraversal(root.right);
        
        return list;
    }
}

中序遍历（Inorder Traversal）

访问顺序：中序遍历左子树、根节点、中序遍历右子树
下图中序遍历的结果是：1、2、3、4、5、7、8、9、10、11、12

另一种中序遍历访问顺序：中序遍历右子树、根节点、中序遍历左子树
则下图的中序遍历的结果是：12、11、10、9、8 、7、5、4、3、2、1

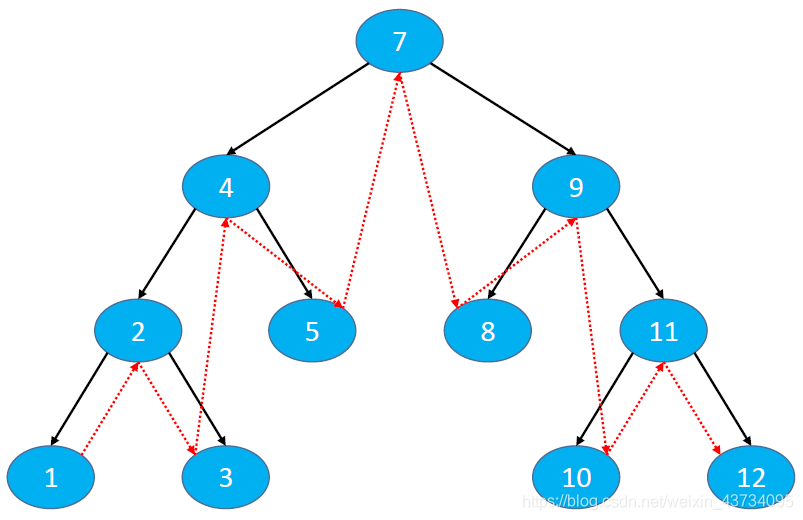
二叉搜索树的中序遍历结果是升序或者降序的；

二叉树的中序遍历： https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
	List<Integer> list = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
    	if(root == null) return list;
    	inorderTraversal(root.left);
    	list.add(root.val);
    	inorderTraversal(root.right);
    	return list;
    }
}

后序遍历（Postorder Traversal）

访问顺序：后序遍历左子树、后序遍历右子树、根节点
下图的后序遍历的结果是：1、3、2、5、4、8、10、12、11、9、7

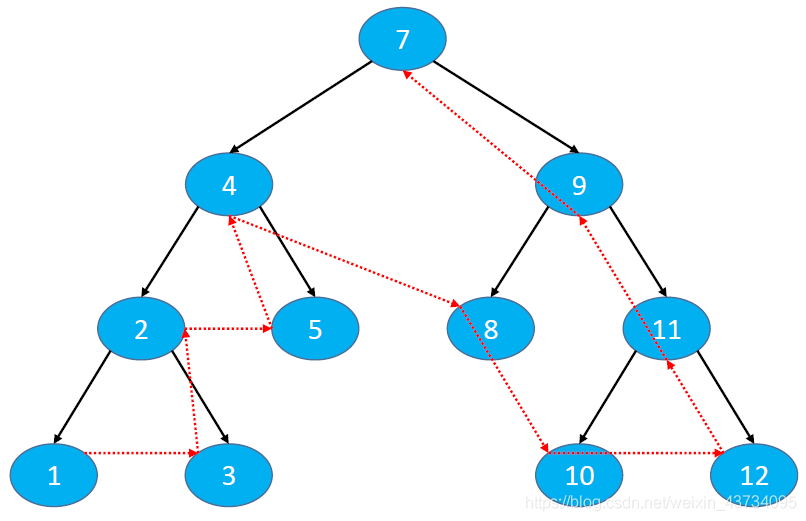
二叉树的后序遍历： https://leetcode-cn.com/problems/binary-tree-postorder-traversal/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
	List<Integer> list = new ArrayList<Integer>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if(root == null) return list;
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        list.add(root.val);
        return list;
    }
}

层序遍历（Level Order Traversal）

访问顺序：从上到下、从左到右依次访问每一个节点
下图的层序遍历的结果是：7、4、9、2、5、8、11、1、3、10、12

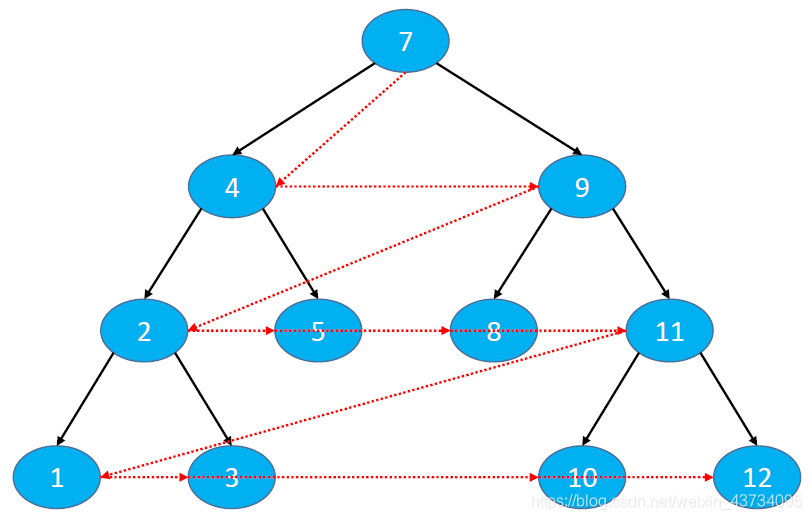
二叉树的层次遍历： https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
	List<List<Integer>> resList = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
    	if(root == null) return resList;
    	
    	Queue<TreeNode> queue = new LinkedList<>();
    	int levelSize = 1;
    	queue.offer(root);
    
    	
    	List<Integer> list = new ArrayList<>(); ;
    	while(!queue.isEmpty()){
    		TreeNode node = queue.poll();
    		list.add(node.val);
    		levelSize--;
    		
    		if(node.left != null){
    			queue.offer(node.left);
    		}
    		if(node.right != null){
    			queue.offer(node.right);
    		}

    		if(levelSize == 0){
    			resList.add(list);
                levelSize = queue.size();
    			list = new ArrayList<>();
    		}
    	}
    	return resList;
    }
}

根据遍历结果重构二叉树

以下结果可以保证重构出唯一的一棵二叉树：

• 前序遍历 + 中序遍历
• 后序遍历 + 中序遍历

前序遍历 + 后序遍历：

• 如果它是一棵真二叉树（Proper Binary Tree），结果是唯一的
• 不然结果不唯一

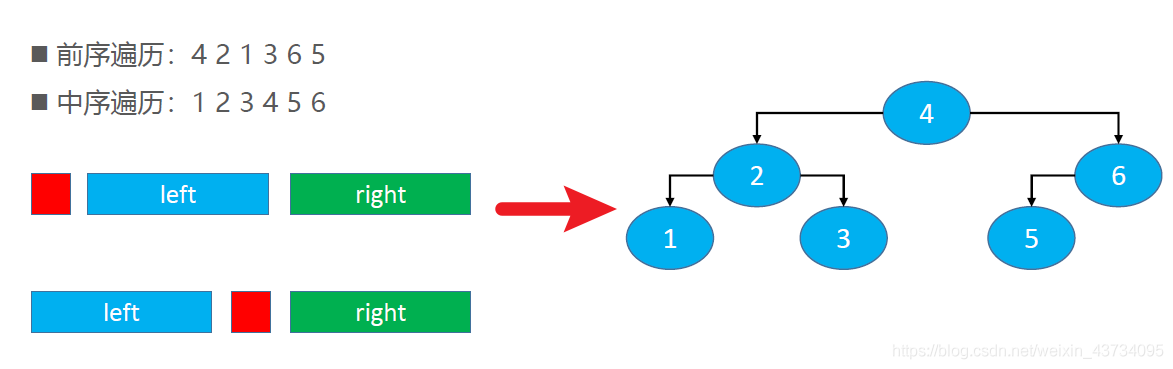
前序遍历+中序遍历 重构二叉树

四则运算

四则运算的表达式可以分为3种：

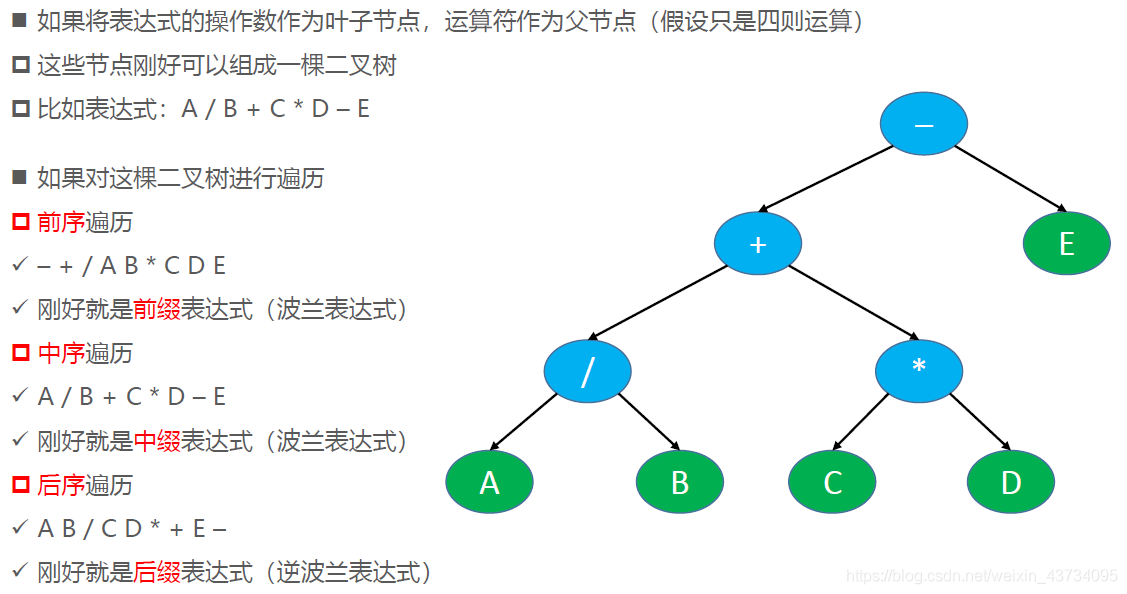
• 前缀表达式（prefix expression），又称为波兰表达式
• 中缀表达式（infix expression）
• 后缀表达式（postfix expression），又称为逆波兰表达式

表达式树

练习

翻转二叉树

226_翻转二叉树：https://leetcode-cn.com/problems/invert-binary-tree/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
	public TreeNode invertTree(TreeNode root) {
		if(root == null) return root;
		
		Queue<TreeNode> queue = new LinkedList<>();
		queue.offer(root);
		while(!queue.isEmpty()){
			TreeNode node = queue.poll();
			
			TreeNode treeNode = node.left;
			node.left = node.right;
			node.right = treeNode;
			
			if(node.left != null){
				queue.offer(node.left);
			}
			if(node.right != null){
				queue.offer(node.right);
			}
		}
		return root;
	}
}

二叉树的最大深度

104_二叉树的最大深度：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
    	if(root == null) return 0;
    	return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}