数值计算方法 线性方程组的数值解法(4)---向量和矩阵范数(norm) 高斯-赛德尔(Gauss-Seidel)迭代、共轭梯度(Conjugate Gradient)迭代

(范数部分matlab有现成函数，若有需要直接参照matlab_norm)

向量范数
设 $\boldsymbol x\in \boldsymbol R^n$则范数||x||满足： $||\boldsymbol x|| \ge 0$当且仅当x=0,||x||=0。任意实数λ $||\lambda\boldsymbol x||=|\lambda|||\boldsymbol x||$且对任意向量满足三角不等式 $||\boldsymbol{x+y}||\le ||\boldsymbol x||+||\boldsymbol y||$常见范数：
1-范数 $||\boldsymbol x||_1=\sum_{i=1}^n|x_i|$2-范数 $||\boldsymbol x||_2=(\sum_{i=1}^nx_i^2)^{\frac{1}{2}}$∞-范数 $||x||_{\infty}=max_{1\le i\le n}|x_i|$1、∞的证明简单。证明2-范数时，需用 $(x_1y_1+x_2y_2+...+x_ny_n)^2\le (x_1^2+x_2^2+...+x_n^2)(y_1^2+...+y_n^2)$这种求和形式的柯西施瓦茨不等式用数学归纳法即可证明。这些范数统一写作p-范数 $||\boldsymbol x||_p=(\sum_{i=1}^n|x_i|^p)^{\frac{1}{p}}$如果存在与x无关的正常数c₁c₂分别乘||x||_a能将||x||_b夹在中间，称这两种范数等价。以∞-范数为媒介，容易证明有限维上不同范数是等价的。
matlab中求向量范数使用norm(v)，默认2-范数。若想指定p值，传入两个参数norm（vector,p）即可。实例见matlab_norm
矩阵范数
定义如下 $||\boldsymbol A||=\max\limits_{\boldsymbol{x\ne 0}}\frac{||\boldsymbol {Ax}||}{||\boldsymbol x||}$理解此式，列向量x的维度应等于A的列数，乘出来的向量是维度为A的行数的列向量，所以维度不一定和分母相同。不好理解的是与矩阵无关的向量x，只要非0都可选，而且按照确定范数规则能得到统一的最大值。后面证明无穷范数时会理解一些。
将矩阵范数定义移项得到 $||\boldsymbol {Ax}||\le ||\boldsymbol A||~||\boldsymbol x||$称为相容性条件。向量范数定义中的三个条件，矩阵范数也满足。此外，还有 $||\boldsymbol {AB}||\le ||\boldsymbol A||~||\boldsymbol B||$AB是同维方阵。此式课本证明有点紊乱，调整如下：
$||\boldsymbol{ABx}||=||\boldsymbol{A(Bx)}||$由于矩阵同维，所以可以进行如上操作。显然，Bx变成了向量。所以根据相容性条件， $||\boldsymbol{ABx}||\le\boldsymbol{||A||~||Bx}||$所以 $||\boldsymbol {AB}||=\max\limits_{\boldsymbol{x\ne 0}}\frac{||\boldsymbol {ABx}||}{||\boldsymbol x||} \le\max\limits_{\boldsymbol{x\ne 0}}\frac{||\boldsymbol {A||~||Bx}||}{||\boldsymbol x||}$所以 $||\boldsymbol {AB}||\le||\boldsymbol A||\max\limits_{\boldsymbol{x\ne 0}}\frac{||\boldsymbol {Bx}||}{||\boldsymbol x||}=||\boldsymbol {A||~||B}||$

对n 阶方阵A=（a_ij）_n有 $||\boldsymbol {A}||_\infty=\max\limits_{1\le i\le n}\sum_{j=1}^n|a_{ij}|$ $||\boldsymbol {A}||_1=\max\limits_{1\le j\le n}\sum_{i=1}^n|a_{ij}|$ $||\boldsymbol {A}||_2=\sqrt{\lambda_{max}(\boldsymbol{A^TA)}}$这部分书中证明比较流畅，直接摘录如下：(源自《数值计算方法》，马东升等著，机械工业出版社)


所以

以上还是比较晦涩的。我解释如下：(注意以上证明的式子只适用于方阵)矩阵范数的难点在找合适的x向量。注意到在无穷范数定义式 $||\boldsymbol A||_\infty=\max\limits_{\boldsymbol{x\ne 0}}\frac{||\boldsymbol {Ax}||_\infty}{||\boldsymbol x||_\infty}$中，分母又除掉了x中的最大量。对于能够使得 $\frac{||\boldsymbol {Ax}||_\infty}{||\boldsymbol x||_\infty}$取到最大值的向量 $\boldsymbol x=\begin{pmatrix}x_1\\x_2\\x_3\\...\\x_n\end{pmatrix}$设 $x_k=\max\limits_{0\le i\le n}|x_i|$则显然 $\frac{||\boldsymbol {A}(\boldsymbol x/x_k)||_\infty}{||\boldsymbol x/x_k||_\infty}$也应该取得最大值。所以 $\textbf x /x_k$也是能够使A范数到达最大值的向量，而且它的∞-范数是1.也就是对所有满足条件的x，都不妨除以它里面绝对值最大的元素单位化成所有元素的绝对值都在0到1之间的向量。这时就有 $||\textbf A||_\infty=\max\limits_{||\textbf x||_\infty=1}||\textbf {Ax}||_\infty$
接下来，需要让A中所有元素“尽其所能”来达到最大。例如对矩阵 $\boldsymbol A = \begin{pmatrix}1&-2&6\\2&3&4\\-5&4&3\end{pmatrix}$右乘无穷范数为1、元素绝对值不超过1的1 * 3列向量使得到的1 * 3列向量某个元素达到值所有可能性的最大值，根据 $\textbf {(Ax)}_i=\sum_{j=1}^3a_{ij}x_j$显然要取某一行元素绝对值和最大的元素，对应的x向量取1或-1才能实现。对应地，应该取A的第三行，x取[-1;1;1] (列向量)。最终得到的结果就是 $||\boldsymbol {A}||_\infty=\max\limits_{1\le i\le n}\sum_{j=1}^n|a_{ij}|=12$

高斯-赛德尔迭代法
等式Ax=b标量形式写作 $\sum_{j=1}^nA_{ij}x_{j}=b_i,i=1,2,...,n$将含有x_i的一项提出来，写作 $A_{ii}x_i+\sum_{j=1,j\ne i}^nA_{ij}x_j=b_i,i=1,2,...,n$解x_i，得到 $x_i=\frac{1}{A_{ii}}(b_i-\sum_{j=1,j\ne i}^nA_{ij}x_j),i=1,2,...,n$写成动态形式 $x_i\leftarrow\frac{1}{A_{ii}}(b_i-\sum_{j=1,j\ne i}^nA_{ij}x_{j}),i=1,2,...,n$可以看出一旦求出x_i的某个新值x_i^k+1，就用新值代替老值做某步剩下的计算。这是它与雅可比迭代法的区别。在雅可比迭代法中，每一个大步都用上次迭代得到的值。高斯-赛德尔迭代通常效果更好些，但某些情况会出现雅可比迭代法收敛而高斯-赛德尔迭代法发散的情况。首先选取初值x。如果不知道怎么选好点，就可以随机选。将上式每次得到的结果再代入上式，相邻两次迭代的x的差距小到一个标准。
松弛法加速
将前一步的 $x_i^{(k)}$与高斯-赛德尔方法的迭代值 $\widetilde{x_i}^{(k+1)}$适当加权平均，以获得更好的近似值 $x_i^{k+1}$。对应的式子写作 $x_i\leftarrow \frac{w}{A_{ii}}(b_i-\sum_{j=1,j\ne i}^nS_{ij}x_j)+(1-w)x_i,i=1,2,...,n$此外还有超松弛方法(SOR)，Ω设在1和2之间(为保证收敛性，需要在0和2之间)。在代码实现中，只需改变omega参数即可。Ω=1对应的是高斯-赛德尔迭代法。有些将w的推荐值设在 $\omega_{opt}\approx\frac{2}{1+\sqrt{1-(\Delta x^{k+p}/\Delta x^(k))^{1/p}}}$这里综合以上几种方法写一段基本普适各种情况代码。实现的思路是：先执行大约10次高斯-赛德尔迭代，然后记录Δx^(k)的值；然后依次进行p次迭代，记录最后一次迭代的Δx^k+p的值，最后使用松弛法加速，按照上述松弛因子ω公式最后得出结果。
用到的函数：
matlab_按元素乘(这里用来求内积)
matlab_抛出错误
matlab_输入参数个数nargin
运行句柄函数feval

function [x,numIteration,omega] = gaussSeidel(func,x,maxIteration,epsilon)
% 输入的func是迭代函数句柄
% x是初始化的向量，maxIteration是最大允许的迭代次数 (默认500)
% epsilon是允许的误差 (默认1.0e-7)
% 输出的x是解得的值
% numIteration是迭代次数
% omega是松弛因子
if nargin < 4; epsilon = 1.0e-7; end
if nargin < 3; maxIteration = 500; end
k = 10; p = 1; omega = 1;
for numIteration = 1:maxIteration
    xOld = x;
    x = feval(func,x,omega);
    dx = sqrt(dot(x - xOld,x - xOld));%求两次迭代解的差的内积
    if dx < epsilon; 
    	return;%退出函数 
    end
    if numIter == k; dx1 = dx; end
    if numIter == k + p
        omega = 2/(1 + sqrt(1 - (dx/dx1)^(1/p)));
    end
end
error('迭代次数超要求')

当然，基础的写法是

function [x] = gaussSeidelBasic(func,x)
dx=1;
while dx > 1.0e-7
    xOld = x;  x = feval(func,x);
    dx = sqrt(dot(x - xOld,x - xOld));
end

例如，解以前描述过的以三对角矩阵为系数矩阵的方程 $\begin{pmatrix}-2&1&0&0&...&0&0&0&1\\-1&2&-1&0&...&0&0&0&0\\0&-1&2&-1&...&0&0&0&0\\...\\0&0&0&0&...&-1&2&-1&0\\0&0&0&0&...&0&-1&2&-1\\1&0&0&0&...&0&0&-1&2\end{pmatrix}\begin{pmatrix}x_1\\x_2\\...\\...\\...\\..\\x_n\end{pmatrix}=\begin{pmatrix}0\\0\\0\\0\\0\\..\\1\end{pmatrix}$其中n=20。根据 $x_i=\frac{1}{A_{ii}}(b_i-\sum_{j=1,j\ne i}^nA_{ij}x_j),i=1,2,...,n$有

function x = functionSol(x,omega)
% 为上述方程书写迭代函数
n = length(x);
x(1) = omega*(x(2) - x(n))/2 + (1-omega)*x(1);
for i = 2:n-1
    x(i) = omega*(x(i-1) + x(i+1))/2 + (1-omega)*x(i);
end
x(n) = omega *(1 - x(1) + x(n-1))/2 + (1-omega)*x(n);

在命令行中书写

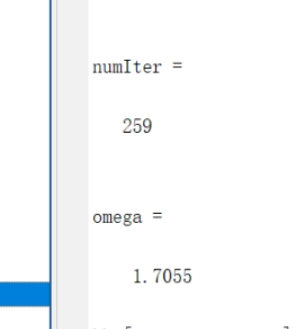
[x,numIter,omega] = gaussSeidel(@functionSol,zeros(20,1))

算得结果

这里精确到1.0e-9，迭代了259次。

当然，如果采用不带松弛的高斯赛德尔迭代，迭代方程就写作

function x = functionSol(x)
% 为上述方程书写迭代函数
n = length(x);
x(1) =(x(2) - x(n))/2 ;
for i = 2:n-1
    x(i) =(x(i-1) + x(i+1))/2 ;
end
x(n) =(1 - x(1) + x(n-1))/2 ;

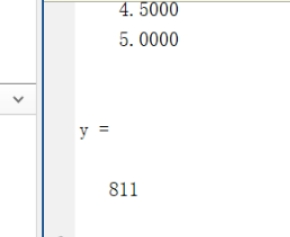
在那个简单写法里加个计数器，在命令行里输入

[x,y] = gaussSeidelBasic(@functionSol,zeros(20,1))

数值结果相同，但迭代了811次。可见，松弛法有显著的加速效果。

迭代公式的矩阵表示

迭代原理：已知 $\textbf{Ax=b}$设找到一个等价方程组 $\textbf{x=Bx+f}$建立迭代格式 $\textbf{x}^{k+1}=\textbf {Bx}^k+\textbf f,k=0,1,...$使得x收敛于x* $\lim_{k\rightarrow +\infty}\boldsymbol x^{(k)}=\boldsymbol x^*$则x*就是解。对于一般的线性方程组，将系数矩阵分解成 $\boldsymbol{A=-L+D+U}$以高斯-赛德尔公式为例(雅可比迭代在此未详细讨论，因为与之同理) $x_i=\frac{1}{A_{ii}}(b_i-\sum_{j=1,j\ne i}^nA_{ij}x_j),i=1,2,...,n$用向量形式展成 $\boldsymbol x^{(k+1)}=\boldsymbol D^{-1}(\boldsymbol b+ \boldsymbol {Lx}^{(k+1)}+\boldsymbol {Ux}^k)$（注意上式中的变号问题）左乘D使之移到左侧，将含有x^(k+1)的项移到一起，得到 $\textbf{x}^{k+1}=\textbf {Bx}^k+\textbf f,k=0,1,...$其中， $\boldsymbol {b=(D-L)}^{-1}\boldsymbol U$ $\boldsymbol {f=(D-L)}^{-1}\boldsymbol b$B也作G，称为高斯-赛德尔迭代法的迭代矩阵。松弛矩阵也有矩阵表示法，再此不再赘述。从此就可以引入
共轭梯度法
共轭梯度法连同上述SOL方法，是人工智能等领域比较活跃的算法，理论上用n此迭代就可以找到精确解。在实际中，需要使用3n~5n次迭代。
寻找一个向量x，使函数 $f(x)=\frac{1}{2}x^TAx-b^Tx$最小。其中A是对称正定阵。看出f(X)在梯度为0处取得最小值，梯度为0时 $Ax=b$恰巧成立。将其与解非线性数值方程最速下降法相比对：共轭方向法是在N维优化问题中，每次沿一个方向优化得到极小值，后面再沿其他方向求极小值不影响前面已经得到的沿那些方向上的极小值。这组方向两两共轭，所以就叫共轭方向法。梯度下降法每次都直接选取当前点的梯度方向，有可能出现这次求出的极小值点在之前搜索过的方向上又不是极小值的情况。代码实现如下：

function [x,numIter] = conjGrad(func,x,b,epsilon)

% func = handle of function that returns the vector A*v
% x = 初始化解向量
% b = constant vector in A*x = b
% epsilon = 最大误差 (默认1.0e-9)
% x 输出的解
% numIter 执行迭代的次数
if nargin == 3; epsilon = 1.0e-9; end
n = length(b);
r = b - feval(func,x); s = r;
for numIter = 1:n
    u = feval(func,s);
    alpha = dot(s,r)/dot(s,u);
    x = x + alpha*s;
    r = b - feval(func,x);  
    if sqrt(dot(r,r)) < epsilon
        return
    else
        beta = -dot(r,u)/dot(s,u);
        s = r + beta*s;
    end
end
error('Too many iterations')

仍然举高斯-赛德尔迭代法中的例子 $\begin{pmatrix}-2&1&0&0&...&0&0&0&1\\-1&2&-1&0&...&0&0&0&0\\0&-1&2&-1&...&0&0&0&0\\...\\0&0&0&0&...&-1&2&-1&0\\0&0&0&0&...&0&-1&2&-1\\1&0&0&0&...&0&0&-1&2\end{pmatrix}\begin{pmatrix}x_1\\x_2\\...\\...\\...\\..\\x_n\end{pmatrix}=\begin{pmatrix}0\\0\\0\\0\\0\\..\\1\end{pmatrix}$其中n=20.
需要将迭代函数重写成矩阵形式。如下：

function Av = functionSol(v)
n = length(v);
Av = zeros(n,1);
Av(1) = 2*v(1) - v(2) + v(n);
Av(2:n-1) = -v(1:n-2) + 2*v(2:n-1) - v(3:n);
Av(n) = -v(n-1) + 2*v(n) + v(1);

在命令行中输入

[x,numIter] = conjGrad(@functionSol,x,b)

得到


可见，使用共轭梯度法，迭代次数大幅减少。