2020-2-19 深度学习笔记9 - 卷积网络1（卷积运算，动机-稀疏交互、参数共享、等变表示）

第九章 卷积网络

官网

卷积网络（convolutional network），也叫作卷积神经网络（convolutional neural network，CNN），是一种专门用来处理具有类似网格结构的数据的神经网络。

卷积网络提供了一种方法来特化神经网络，使其能够处理具有清楚的网格结构拓扑的数据，以及将这样的模型扩展到非常大的规模。 这种方法在二维图像拓扑上是最成功的。

卷积是一种特殊的线性运算。

【补充-为什么要使用卷积？】

在传统的神经网络中，比如多层感知机（MLP），其输入通常是一个特征向量：需要人工设计特征，然后将这些特征计算的值组成特征向量。在过去几十年的经验来看，人工找到的特征并不是怎么好用，特征有时多了（需要PCA降维），特征有时少了（容易过拟合），有时选择的特征根本就不起作用（真正起作用的特征在浩瀚的未知里面）。这就是为什么在过去卷积神经网络一直被SVM等完虐的原因。

如果特征都是从图像中提取的，那如果把整副图像作为特征来训练神经网络不就行了，那肯定不会有任何信息丢失！那先不说一幅图像有多少冗余信息，单说着信息量就超级多。。。假如有一幅1000*1000的图像，如果把整幅图像作为向量，则向量的长度为1000000（10⁶）。再假如隐含层神经元的个数和输入一样，也是1000000；那么，输入层到隐含层的参数数据量有10¹²，什么样的机器能训练这样的网络呢。所以，我们还得降低维数，同时得以整幅图像为输入（人类实在找不到好的特征了）。于是，牛逼的卷积来了。

CNN卷积神经网络层级结构如下

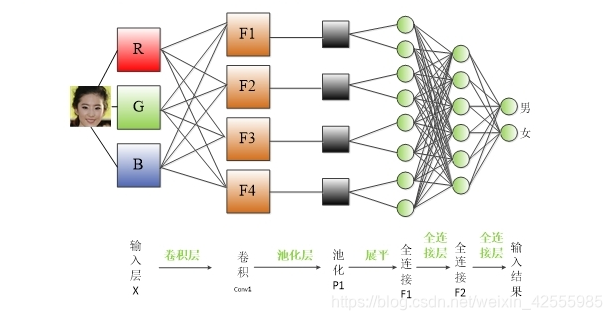
CNN网络一共有5个层级结构：
输入层、卷积层、激活层、 池化层、全连接FC层

卷积运算

在通常形式中，卷积convolution是对两个实变函数的一种数学运算。

关于卷积介绍参见（通俗易懂） https://www.zhihu.com/question/22298352?rf=21686447

卷积的连续（上）和离散（下）定义式子有一个共同的特征：

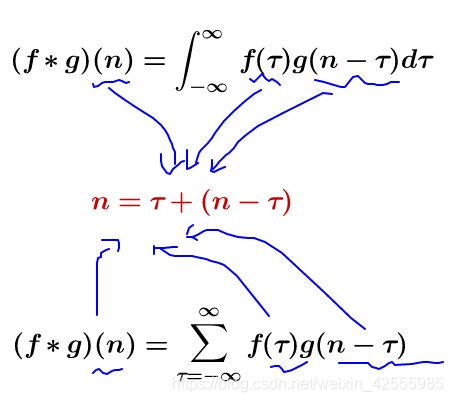
我们令 $x=\tau,y=n-\tau$，那么 $x+y=n$ 就是下面这些直线：

如果遍历这些直线，就好比，把毛巾沿着角卷起来：

卷积的含义解释：
先对g函数进行翻转，相当于在数轴上把g函数从右边褶到左边去，也就是卷积的“卷”的由来。
然后再把g函数平移到n，在这个位置对两个函数的对应点相乘，然后相加，这个过程是卷积的“积”的过程。

再说的直接一点：所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加。

在连续情况下，叠加指的是对两个函数的乘积求积分，在离散情况下就是加权求和，为简单起见就统一称为叠加。

整个卷积过程就是：翻转——>滑动——>叠加——>滑动——>叠加——>滑动——>叠加…

多次滑动得到的一系列叠加值，构成了卷积函数。

卷积的“卷”，指的的函数的翻转，从 g(t) 变成 g(-t) 的这个过程；同时，“卷”还有滑动的意味在里面（吸取了网友李文清的建议）。如果把卷积翻译为“褶积”，那么这个“褶”字就只有翻转的含义了。

卷积的“积”，指的是积分/加权求和。

举例1：丢骰子
有两枚骰子，把它们都抛出去，两枚骰子点数加起来为4的概率是多少?

分析一下，两枚骰子点数加起来为4的情况有三种情况：1+3=4， 2+2=4, 3+1=4
因此，两枚骰子点数加起来为4的概率为：

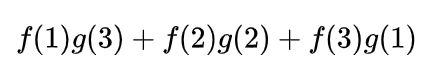
​​写成卷积的方式就是
$(f*g)(4)=\sum_m=1^3f(4-m)g(m)$

在这里我们进一步用上面的翻转滑动叠加的逻辑进行解释。

首先，因为两个骰子的点数和是4，为了满足这个约束条件，我们还是把函数 g 翻转一下，然后阴影区域上下对应的数相乘，然后累加，相当于求自变量为4的卷积值，如下图所示：

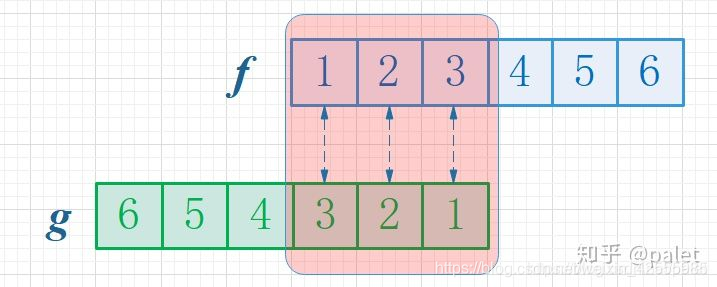
​​进一步，如此翻转以后，可以方便地进行推广去求两个骰子点数和为 n 时的概率，为f 和 g的卷积 f*g(n)，如下图所示：​

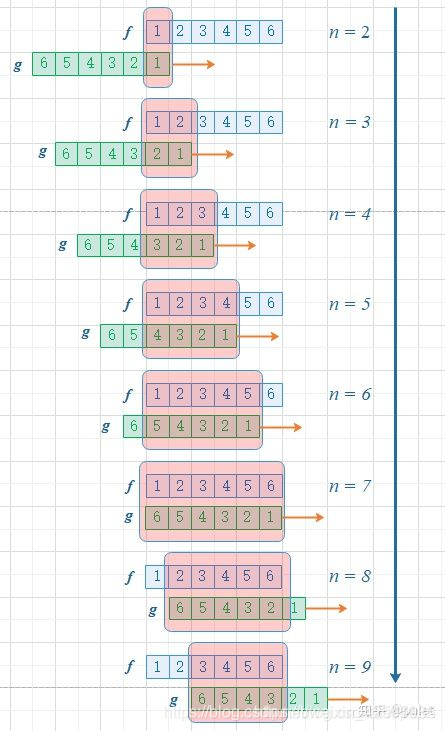
由上图可以看到，函数 g 的滑动，带来的是点数和的增大。这个例子中对f和g的约束条件就是点数和，它也是卷积函数的自变量。有兴趣还可以算算，如果骰子的每个点数出现的概率是均等的，那么两个骰子的点数和n=7的时候，概率最大。

举例2，图像处理

对上面图像的处理函数（如平滑，或者边缘提取），也可以用一个g矩阵来表示，如：

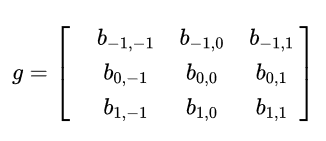
注意，我们在处理平面空间的问题，已经是二维函数了，相当于：
$f(x,y)=a_{x,y}$ , $g(x,y)=b_{x,y}$

那么函数 f 和 g 的在（u，v）处的卷积 $f*g(u,v)$ 该如何计算呢？

按卷积的定义，二维离散形式的卷积公式应该是： $(f*g)(u,v)=\sum_i\sum_jf(i,j)g(u-i,v-j)=\sum_i\sum_ja_{i,j}b_{u-i,v-j}$
从卷积定义来看，应该是在x和y两个方向去累加（对应上面离散公式中的i和j两个下标），而且是无界的，从负无穷到正无穷。可是，真实世界都是有界的。例如，假设上面列举的图像处理函数g实际上是个3x3的矩阵，意味着，在除了原点附近以外，其它所有点的取值都为0。考虑到这个因素，上面的公式其实退化了，它只把坐标（u,v）附近的点选择出来做计算了。所以，真正的计算如下所示：

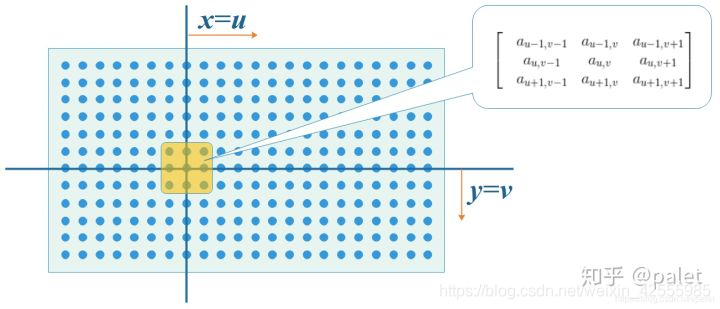
首先我们在原始图像矩阵中取出（u,v）处的矩阵

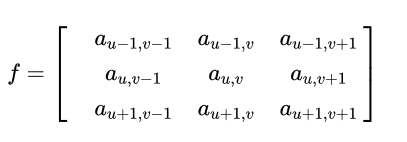
然后将图像处理矩阵翻转（这个翻转有点意思，可以有几种不同的理解，其效果是等效的：（1）先沿x轴翻转，再沿y轴翻转；（2）先沿x轴翻转，再沿y轴翻转；）。
原始矩阵：
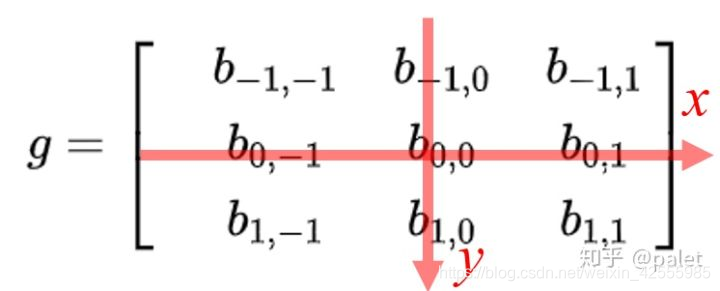翻转后的矩阵：

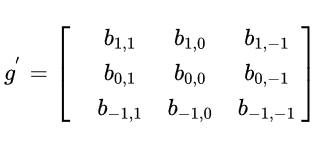
（1）先沿x轴翻转，再沿y轴翻转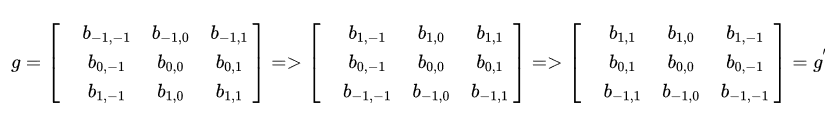（2）先沿y轴翻转，再沿x轴翻转
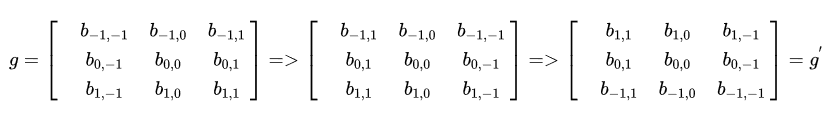计算卷积时，就可以用 f 和 g’ 的内积：

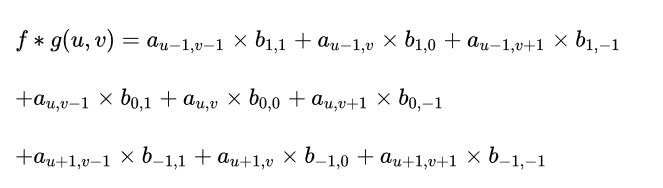
请注意，以上公式有一个特点，做乘法的两个对应变量a,b的下标之和都是（u,v），其目的是对这种加权求和进行一种约束。这也是为什么要将矩阵g进行翻转的原因。以上矩阵下标之所以那么写，并且进行了翻转，是为了让大家更清楚地看到跟卷积的关系。这样做的好处是便于推广，也便于理解其物理意义。实际在计算的时候，都是用翻转以后的矩阵，直接求矩阵内积就可以了。

以上计算的是（u,v）处的卷积，延x轴或者y轴滑动，就可以求出图像中各个位置的卷积，其输出结果是处理以后的图像（即经过平滑、边缘提取等各种处理的图像）。

再深入思考一下，在算图像卷积的时候，我们是直接在原始图像矩阵中取了（u,v）处的矩阵，为什么要取这个位置的矩阵，本质上其实是为了满足以上的约束。因为我们要算（u,v）处的卷积，而g矩阵是3x3的矩阵，要满足下标跟这个3x3矩阵的和是（u,v），只能是取原始图像中以（u,v）为中心的这个3x3矩阵，即图中的阴影区域的矩阵。

推而广之，如果如果g矩阵不是3x3，而是7x7，那我们就要在原始图像中取以（u,v）为中心的7x7矩阵进行计算。由此可见，这种卷积就是把原始图像中的相邻像素都考虑进来，进行混合。相邻的区域范围取决于g矩阵的维度，维度越大，涉及的周边像素越多。而矩阵的设计，则决定了这种混合输出的图像跟原始图像比，究竟是模糊了，还是更锐利了。

比如说，如下图像处理矩阵将使得图像变得更为平滑，显得更模糊，因为它联合周边像素进行了平均处理【注意：原图的处理实际上用的是正态分布矩阵，这里为了简单，就用了算术平均矩阵】：

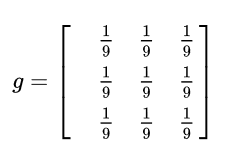
而如下图像处理矩阵将使得像素值变化明显的地方更为明显，强化边缘，而变化平缓的地方没有影响，达到提取边缘的目的：

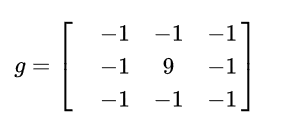
其他例子还有信号分析，见链接。

以下是《机器学习》原书中解释

假设我们正在用激光传感器追踪一艘宇宙飞船的位置。 我们的激光传感器给出一个单独的输出 $x(t)$，表示宇宙飞船在时刻 $t$ 的位置。 $x$和 $t$都是实值的，这意味着我们可以在任意时刻从传感器中读出飞船的位置。

现在假设我们的传感器受到一定程度的噪声干扰。 为了得到飞船位置的低噪声估计，我们对得到的测量结果进行平均。 显然，时间上越近的测量结果越相关，所以我们采用一种加权平均的方法，对于最近的测量结果赋予更高的权重。 我们可以采用一个加权函数 $w(a)$ 来实现，其中 $a$表示测量结果距当前时刻的时间间隔。 如果我们对任意时刻都采用这种加权平均的操作，就得到了一个新的对于飞船位置的平滑估计函数 $s$：
$s(t)=∫x(a)w(t−a)da$

这种运算就叫做卷积。 卷积运算通常用星号表示：
$s(t)=(x∗w)(t)$
在卷积网络的术语中，卷积的第一个参数（在这个例子中，函数 $x$）通常叫做输入，第二个参数（函数 $w$）叫做核函数。 输出有时被称作特征映射。

离散形式的卷积：
$s(t)=(x∗w)(t)=\sum_{a=−∞}^∞x(a)w(t−a)$

最后，我们经常一次在多个维度上进行卷积运算。 例如，如果把一张二维的图像 $I$作为输入，我们也许也想要使用一个二维的核 $K$：
$S(i,j)=(I∗K)(i,j)=\sum_m\sum_nI(m,n)K(i−m,j−n)$
卷积是可交换的(commutative)，我们可以等价地写作：
$S(i,j)=(K∗I)(i,j)=\sum_m\sum_nI(i−m,j−n)K(m,n).$
卷积运算可交换性的出现是因为我们将核相对输入进行了翻转，从 $m$增大的角度来看，输入的索引在增大，但是核的索引在减小。
但是许多神经网络库会实现一个相关的函数，称为互相关函数，和卷积运算几乎一样但是并没有对核进行翻转：
$S(i,j)=(I∗K)(i,j)=\sum_m\sum_nI(i+m,j+n)K(m,n)$
许多机器学习的库实现的是互相关函数但是称之为卷积。

离散卷积可以看作矩阵的乘法。

动机

卷积运算通过三个重要的思想来帮助改进机器学习系统：稀疏交互、参数共享、等变表示。

• 稀疏交互

卷积网络具有稀疏交互（也叫稀疏连接或者稀疏权重）的特征。

例如，当处理一张图像时，输入的图像可能包含成千上万个像素点，但是我们可以通过只占几个到上百个像素点来检测一些小的有意义的特征，比如图像边缘。这意味着我们需要存储的参数更少，不仅减少了模型的存储需求，而且提高了他的统计效率。稀疏的图形化解释如图9.2和图9.3所示。
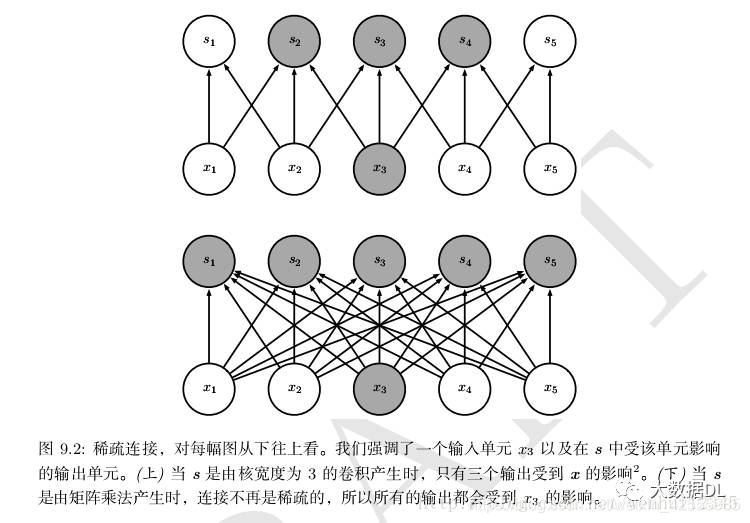
在深度卷积网络中，处在网络深层的单元可能与绝大部分输入是间接交互的，如图9.4所示。这允许网络可以通过只描述稀疏交互的基石来高效地描述多个变量的复杂交互。

• 参数共享

参数共享是指在一个模型的多个函数中使用相同的参数。

区别：
【传统神经网络】当计算一层的输出时，权重矩阵的每一个元素只使用一次，当它乘以输入的一个元素后就再也不会用到了。
【卷积神经网络】核的每一个元素都作用在输入的每一位置上（是否考虑边界像素取决于对边界决策的设计）。卷积运算中的参数共享保证了我们只需要学习一个参数集合，而不是对于每一位置都需要学习一个单独的参数集合。

下图演示了参数共享时如何实现的。

一个实际例子，图9.6说明了稀疏连接和参数共享时如何显著提高线性函数在一张图像上进行边缘检测的效率。
- 等变表示

对于卷积，参数共享的特殊形式使得神经网络层具有对平移等变的性质。 如果一个函数满足输入改变，输出也以同样的方式改变这一性质，我们就说它是**等变(**equivariant)的。

举个例子，令 $I$表示图像在整数坐标上的亮度函数， $g$表示图像函数的变换函数（把一个图像函数映射到另一个图像函数的函数）使得 $I’ = g(I)$，其中图像函数 $I’$满足 $I’(x,y) = I(x-1, y)$。 这个函数把 $I$中的每个像素向右移动一个单位。 如果我们先对 $I$进行这种变换然后进行卷积操作所得到的结果，与先对 $I$进行卷积然后再对输出使用平移函数 $g$得到的结果是一样的