2020-2-23 深度学习笔记10 - 序列建模：循环和递归网络 2（双向RNN，基于编码 - 解码的序列到序列结构--不等长输出序列，计算循环神经网络的梯度）

第十章 序列建模：循环和递归网络

官网

2020-2-21 深度学习笔记10 - 序列建模：循环和递归网络 1（展开计算图，循环神经网络–经典 / 导师驱动 / 唯一单向量输出 / 基于上下文RNN建模）

双向RNN

传统的前馈RNN网络都有一个 ‘‘因果’’ 结构，意味着在时刻 t 的状态只能从过去的序列x⁽¹⁾,…,x^(t−1) 以及当前的输入x^(t) 捕获信息。 然而，在许多应用中，我们要输出的 y^(t) 的预测可能依赖于整个输入序列。

例如，在语音识别中，由于协同发音，当前声音作为音素的正确解释可能取决于未来几个音素，甚至潜在的可能取决于未来的几个词，因为词与附近的词之间的存在语义依赖，如果当前的词有两种声学上合理的解释，我们可能要在更远的未来(和过去)寻找信息区分它们。这在手写识别和许多其他序列到序列学习的任务中也是如此。

双向循环神经网络(或双向 RNN)为满足这种需要而被发明。他们在需要双向信息的应用中非常成功，如手写识别，语音识别以及生物信息学。

顾名思义，双向RNN结合时间上从 序列起点开始移动的RNN 和 另一个时间上从序列末尾开始移动的RNN 。下图展示了典型的双向 RNN

1. 逻辑流程图 - 将输入序列映射到等长的输出序列

其中

• h^(t) 代表通过时间向前移动的子 RNN 的状态
• g^(t) 代表通过时间向后移动的子 RNN 的状态。

因此在每个点 t，输出单元 o^(t) 可以受益于输入 h^(t) 中关于过去的相关概要以及输入 g^(t) 中关于未来的相关概要。

这允许输出单元 o^(t) 能够计算同时依赖于过去和未来且对时刻 t 的输入值最敏感的表示，而不必指定 t 周围固定大小的窗口。

基于编码 - 解码的序列到序列结构

这一小节，我们将讨论RNN如何将一个输入序列映射到不等长的输出序列。这在许多场景中都有应用，如语音识别、机器翻译或问答，其中训练集的输入和输出序列的长度通常不相同。

我们经常将RNN的输入称为“上下文”。我们希望产生此上下文的表示C。这个上下文C可能是一个概括输入序列 $X = (x^{(1)} , . . . , x^{(n_x)} )$ 的向量或者向量序列，即神经网络的隐层高维度向量。

实际上，输入长度和输出长度不一致的神经网络并不罕见，DNN和CNN中这种情况都非常常见（例如将图像输入得到手写数字输出），实现这一能力的核心思想就是增加 1 个及以上的隐层，对于RNN也是一样的，隐层起到信息压缩和解压缩的承上启下作用。

这种架构称为编码-解码或序列到序列架构。如下图所示：

这个结构实际上是由两个RNN结构拼接组成的。

(1) 编码器(encoder)或读取器(reader)或输入 (input) RNN 处理输入序列。编码器输出上下文C(通常是最终隐藏状态的简单函数)，C表示输入序列的语义概要；

(2) 解码器(decoder)或写入器 (writer)或输出 (output) RNN 则以固定长度的向量(即上下文C)为条件产生输出序列 $Y = (y^{(1)},...,y^{(n_y)})$。

在序列到序列的架构中，两个 RNN 共同训练以最大化 $logP(y^{(1)},...,y^{(n_y)} | x^{(1)},...,x^{(n_x)})$（训练集中所有 x 和 y 对的损失）。

编码器 RNN 的最后一个状态 $h_{n_x}$通常被当作输入的表示 C 并作为解码器 RNN 的输入。

计算循环神经网络的梯度

循环神经网络中，关于各个参数计算这个损失函数的梯度是计算成本很高的操作。

通过将RNN的计算图展开后可以清楚地看到，梯度计算涉及执行一次前向传播，接着是由右到左的反向传播。运行时间是 O^(τ)，并且不能通过并行化来降低，因为前向传播图是固有循序的，每个时间步只能一前一后地计算。前向传播中的各个状态必须保存，直到它们反向传播中被再次使用，因此内存代价也是 O^(τ)。

应用于展开图且代价为 O^(τ) 的反向传播算法称为通过时间反向传播(back-propagation through time, BPTT)，隐藏单元之间存在循环的网络非常强大但训练代价也很大。

1.举例说明BPTT计算过程

以之前讨论的例子为例计算梯度【经典RCNN】：

计算图的节点包括参数 U, V, W, b 和 c，以及以 t 为索引的节点序列 x^(t), h^(t), o^(t) 和 L^(t)。

对于每一个节点 N，我们需要基于 N 后面的节点的梯度，递归地计算梯度 ∇_NL。我们从紧接着最终损失的节点开始往回递归：

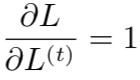
在这个导数中，我们假设输出 o^(t) 作为 softmax 函数的参数，我们可以从 softmax函数可以获得关于输出概率的向量 $\hat y$。我们也假设损失是迄今为止给定了输入后的真实目标 y^(t) 的负对数似然。对于所有 i, t，关于时间步 t 输出的梯度 $\nabla_{o^{(t)}} L$ 如下:

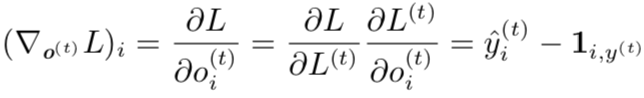
我们从序列的末尾开始，反向进行计算。在最后的时间步 τ, h^(τ) 只有 o^(τ) 作为后续节点，因此这个梯度很简单:

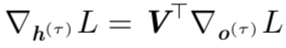
然后，我们可以从时刻 t = τ − 1 到 t = 1 反向迭代，通过时间反向传播梯度，注意h^(t)(t < τ) 同时具有 o^(t) 和 h^(t+1) 两个后续节点。因此，它的梯度由下式计算：

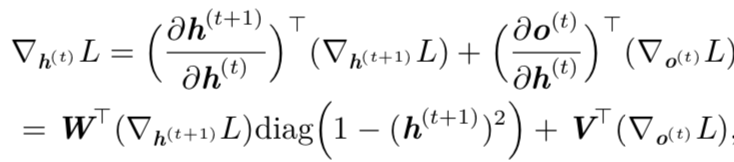
其中 $\text{diag} \Big( 1 - (h^{(t+1)})^2 \Big)$ 表示包含元素 $1 - (h_i^{(t+1)})^2$的对角矩阵。

一旦获得了计算图内部节点的梯度，我们就可以得到关于参数节点的梯度。

因为参数在许多时间步共享，我们必须在表示这些变量的微积分操作时谨慎对待。我们希望使用 bprop 方法计算计算图中单一边对梯度的贡献。然而微积分中的 $\nabla_{W} f$算子，计算 W 对于 f 的贡献时将计算图中的所有边都考虑进去了。为了消除这种歧义，我们定义只在 t 时刻使用的虚拟变量 W^(t) 作为 W 的副本。然后，我们可以使用 $\nabla_{W^{(t)}}$表示权重在时间步 t 对梯度的贡献。

使用这个表示，计算节点内部参数的梯度可以由下式给出:
因为计算图中定义的损失的任何参数都不是训练数据 $x^{(t)}$的父节点，所以我们不需要计算关于它的梯度。