Codeforces Round #663 (Div. 2)

A. Suborrays

题意：

输入一个长度 $n$ ，用 $1 n$ 的数字进行随机排列。定义对于一个正整数 $n$ ，如果对于每一对 $i$ 和 $j(1≤i≤j≤n)$ 都满足，对于 $p$ 的每个子数组，其中所有元素的 $OR$ 不小于该子数列中元素的个数。我们称长度为 $n$ 的排列 $p$ 是好的。

两个数进行位运算了，且范围是 $1~n$ ，那么进行位运算后的结果不会小于元素的个数。简而言之就是：无论怎么输出这个置换序列都是正确的。

AC代码：

int t;
int n,m;
int ans[N];
int main()
{
	sd(t);
	while (t--)
	{
		sd(n);
 
		rep(i,1,n)
		printf("%d%c",i,i==n?'\n':' ');
	}
}

B. Fix You

题意：

给定一个 $n∗m$ 的网格传送带，每个传送带上都有一个方向为， $D$ 代表向下， $R$ 代表向右。我们可以改变传送的的方向。（只能在下右之间做调整。）其中 $(n,m)$ 处为柜台，我们要使得网格传送带上的行李都能到达柜台处，求我们至少要进行多少次操作更改。

因为只有向下和向右，所以把全部的边缘给改变了就行。

AC代码：

const int N = 2010;
 
int t;
int n, m;
char a[200][200];
int main()
{
	sd(t);
	while (t--)
	{
		sdd(n, m);
		rep(i, 1, n)
		{
			rep(j, 1, m)
			{
				cin >> a[i][j];
			}
		}
		int ans = 0;
		rep(i, 1, n - 1)
		{
			if (a[i][m] == 'R')
				ans++;
		}
		rep(j, 1, m - 1)
		{
			if (a[n][j] == 'D')
				ans++;
		}
		pd(ans);
	}
	return 0;
}

C. Cyclic Permutations

题意：

对于所有长度为 $n$ 的排列，找出有多少个满足其中存在至少一个简单环。（对于排列中的每个值 $a[i]$ ，和其左右两边第一个大于它的 $a[j]$ 连一条无向边）

满足条件的排列数等于总排列数-不满足条件的排列数。
而不满足条件的排列数通过找规律：
如 $n = 4$ 时：
不满足条件的排列有：

$1234$
$4321$
$1342$
$2431$
$1243$
$3421$
$1432$
$2341$
一共八个，但可以分为 $4$ 组。一位第 $1,2$ ，第 $3,4$ ，第 $5，6$ ，第 $7,8$ 个排列，分别是 $reverse$ 的。那么只分析第 $1,3,5,7$ 个排列。我们发现。其实规律只与排列中的最小数字 $1$ 和最大数字 $n$ 的位置有关。
如将排列写成 $1…n…$ 形式。则 $1$ 与 $n$ 之间的数字必须升序， $n$ 后的数字必须降序。那么我们只需考虑 $1$ 与 $n$ 之间数字的个数即可。

而 $1$ 与 $n$ 之间数字的个数取值范围是 $[0,n-2]$ ，假如 $1$ 与 $n$ 之间放 $i$ 个数 $（i <= n-2）$ ，又因为这 $i$ 个数一定是升序，所以是组合数 $C_{n-2}^i$ 。

那么可见，不满足条件的排列数为 $2*（C_{n-2}^2+C_{n-2}^1+C_{n-2}^2+…+C_{n-2}^{n-2}）= 2* 2^ n-2 = 2^ {n-1}$ 。
而全排列个数为 $n!$ ，所以答案就是 $n! - 2^ {n-1}$ 。

AC代码：

ll qpow(ll x, ll n, ll mod)
{
	ll res = 1;
	while (n)
	{
		if (n & 1)
			res = (res * x) % mod;
		x = x * x % mod, n >>= 1;
	}
	return res;
}
 
const int N = 2010;
const int mod = 1e9 + 7;
int t;
ll n, m;
char a[200][200];
int main()
{
	sld(n);
	ll ans = 1;
	rep(i, 1, n)
		ans = (ans * i) % mod;
	ans = (ans - qpow(2, n - 1, mod)) % mod;
	pld((ans % mod + mod) % mod);
	return 0;
}

D. 505

题意：

给定一个 $n×m$ 的 $01$ 矩阵，求至少要改多少个元素，使得每个边长为偶数的正方形都包含奇数个 $1$ 。或无解。

若存在边长为 $4$ 的正方形，肯定是无解的。因为将它拆成 $4$ 个边长为 $2$ 的正方形，奇+奇+奇+奇=偶。

扫描二维码关注公众号，回复： 11574562 查看本文章

$n=1$ ：显然答案为 $0$ ；
$n=2$ ：每列的 $1$ 的数量的奇偶性显然只有 $[1,0,1,0,⋯]$ 和 $[0,1,0,1,⋯]$ 两种，都算一下比个大小即可；
$n=3$ ：每列上下两个 $2×1$ 矩阵的1的数量的奇偶性显然只有
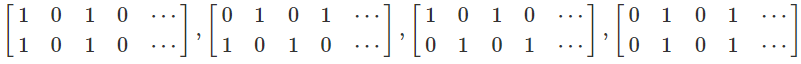
四种，易证每列最多修改 $1$ 次，都算一下比个大小即可。

AC代码：

const int N = 1000000;
int n, m;
vector<string> v;
bool a[4][N + 1];
 
int main()
{
	sdd(n, m);
	if (n >= 4 && m >= 4)
	{
		puts("-1");
		return 0;
	}
	rep(i, 1, n)
	{
		string a;
		cin >> a;
		v.pb(a);
	}
	if (n >= 4)
	{
		rep(i, 1, n)
		{
			rep(j, 1, m)
				a[j][i] = v[i - 1][j - 1] ^ 48;
		}
		swap(n, m);
	}
	else
	{
		rep(i, 1, n)
		{
			rep(j, 1, m)
				a[i][j] = v[i - 1][j - 1] ^ 48;
		}
	}
	if (n == 1)
		puts("0");
	else if (n == 2)
	{
		int ans = 0;
		rep(i, 1, m)
		{
			ans += (a[1][i] ^ a[2][i]) == (i & 1);
		}
		pd(min(ans, m - ans));
	}
	else
	{
		int ans1 = 0, ans2 = 0, ans3 = 0, ans4 = 0;
		rep(i, 1, m)
			ans1 += (a[1][i] ^ a[2][i]) != (i & 1) || (a[2][i] ^ a[3][i]) != (i & 1);
		rep(i, 1, m)
			ans2 += (a[1][i] ^ a[2][i]) == (i & 1) || (a[2][i] ^ a[3][i]) != (i & 1);
		rep(i, 1, m)
			ans3 += (a[1][i] ^ a[2][i]) != (i & 1) || (a[2][i] ^ a[3][i]) == (i & 1);
		rep(i, 1, m)
			ans4 += (a[1][i] ^ a[2][i]) == (i & 1) || (a[2][i] ^ a[3][i]) == (i & 1);
		pd(min(min(ans1, ans2), min(ans3, ans4)));
	}
	return 0;
}