Medidas de distância comuns e medidas de similaridade

No reconhecimento de padrões, mineração de dados, aprendizado de máquina e outros campos, a medição de distância e a medição de similaridade são amplamente utilizadas. Um certo grau de compreensão desses algoritmos de medição pode nos ajudar a lidar melhor e otimizar os problemas encontrados nesses campos.

O algoritmo de medição de distância e o algoritmo de medição de similaridade são algoritmos básicos, frequentemente usados ​​em outros algoritmos mais avançados. Por exemplo, K-Nearest Neighbor (KNN) e K-Means (K-Means) podem usar a distância de Manhattan ou a distância Euclidiana como método de medição.

Este artigo apresenta alguns algoritmos comuns de medição de distância e algoritmos de medição de similaridade.

Descrição da definição do algoritmo, parte do conteúdo é extraído da Enciclopédia Baidu e não será marcado um a um abaixo.

Métricas comuns de distância

Distância de Manhattan

descrição do algoritmo

Distância de Manhattan, também conhecida como distância de táxi, é um termo geométrico usado em um espaço métrico geométrico para indicar a soma das distâncias entre eixos absolutas de dois pontos em um sistema de coordenadas padrão.

A distância de Manhattan pode ser entendida como a distância do caminho.

Usar diagramas para ilustrar é mais intuitivo.

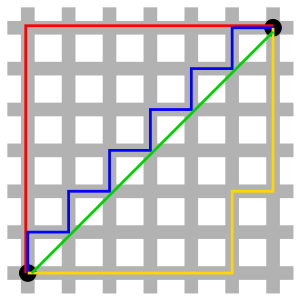
Como mostra a figura, a linha vermelha representa a distância de Manhattan, a linha verde representa a distância euclidiana (a distância em linha reta entre dois pontos no espaço, que será apresentada a seguir), e as linhas azul e amarela representam a Manhattan equivalente distância.

Pode-se observar que em um espaço bidimensional, a distância de Manhattan é a soma dos valores absolutos das diferenças entre as coordenadas horizontal e vertical de dois pontos, ou seja, D ( A , B ) = $D(A,B)=|A_{}-B_{}|+|A_{}-B_{}|$。

Em uma rua da cidade com um layout regular de sul e norte, leste e oeste, a menor distância de deslocamento de um ponto a outro é a menor distância de deslocamento na direção norte-sul mais a menor distância de deslocamento na direção leste-oeste , portanto, a distância de Manhattan também é conhecida como distância de táxi.

Fórmula de cálculo da distância de Manhattan:
$$D(A,B)=\sum _{eu=1}|A_{}-B_{}|$$

Cenário de Aplicação

computação gráfica

Nos primeiros gráficos de computador, a tela é composta de pixels, que são inteiros, e as coordenadas dos pontos são geralmente inteiros.A distância de Manhattan é usada para medir a distância entre dois pontos de pixel AB.

Se você usar a distância euclidiana de AB, deverá realizar cálculos de ponto flutuante, que são caros, lentos e com erros. Se você usar AC e CB, precisará calcular apenas adição e subtração, o que melhora muito a velocidade do cálculo e não importa quantas vezes o cálculo cumulativo seja executado, não haverá erro .

Semelhança

Ele pode ser usado para medir a semelhança de dois vetores, quanto menor a distância, mais semelhantes eles são.

Distância euclidiana

descrição do algoritmo

Distância Euclidiana (Distância Euclidiana), o nome mais acadêmico é Métrica Euclidiana (métrica euclidiana), é uma definição de distância comumente usada, refere-se à distância real entre dois pontos no espaço n-dimensional, ou o comprimento natural do vetor (ou seja, distância do ponto à origem). A distância euclidiana no espaço 2D e 3D é a distância real entre dois pontos.

No diagrama acima descrevendo a distância de Manhattan, a linha verde representa a distância euclidiana entre dois pontos no espaço bidimensional.

Fórmula europeia de cálculo da distância:
$$D(A,B)=\sqrt{(A_{}-B_{}{)}^2+(A_{}-B_{}{)}^2+\cdots +(A_{}-B_{}{)}^2}=\sqrt{\sum _{eu=1}(A_{}-B_{}{)}^2}$$

Cenário de Aplicação

Amplamente utilizado para medir a distância entre dois vetores em um espaço vetorial.

Também é frequentemente usado na medida de similaridade do usuário do sistema de filtragem colaborativa. A classificação do item pelo usuário é abstraída em um vetor de usuário e, em seguida, a distância euclidiana entre dois vetores de usuário é calculada para representar a similaridade entre os usuários: quanto menor a distância, mais semelhante.

distância Chebyshev

descrição do algoritmo

A distância de Chebyshev (distância de Chebyshev), é uma medida no espaço vetorial, a distância entre dois pontos é definida como o valor máximo do valor absoluto da diferença entre os valores das coordenadas.

Fórmula de cálculo da distância de Chebyshev:
$$D(A,B)=\underset{eu}{}\left(|A_{}-B_{}|\right)$$
No xadrez, a distância de um rei a outro ponto é a distância Chebyshev entre dois pontos em um sistema de coordenadas cartesiano bidimensional. Portanto, a distância de Chebyshev também é chamada de distância do tabuleiro de xadrez.

Conforme mostrado na figura abaixo, a posição do rei é f6, e o número na grade representa o número de passos do rei até a grade, ou seja, a distância.

distância de Minkowski

descrição do algoritmo

A distância de Minkowski é uma medida da distância entre dois pontos no espaço de Minkowski.

O espaço de Minkowski refere-se ao espaço-tempo composto de uma dimensão de tempo e três dimensões de espaço na teoria da relatividade especial, que foi expressa pela primeira vez pelo matemático russo-alemão Minkowski (H. Minkowski, 1864-1909). O conceito de espaço de Min e a geometria expressa como uma quantidade de distância especial são consistentes com os requisitos da relatividade restrita.

Portanto, a distância de Min às vezes também se refere ao intervalo de espaço-tempo. Assumindo que existem duas coordenadas A, B e p no espaço n-dimensional são constantes, a distância do tipo Min é definida como
$$D(A,B)=(\sum _{eu=1}{|A_{}-B_{}|}^p{)}^{\frac{}{p}}$$

Perceber:

(1) A distância de Min está relacionada à dimensão dos parâmetros característicos, e a distância de Min com parâmetros característicos de diferentes dimensões geralmente não tem sentido.

(2) A distância de Min não considera a correlação entre os parâmetros do recurso, enquanto a distância de Mahalanobis (distância de Mahalanobis) resolve esse problema.

algumas exceções

A distância de Min pode ser considerada como a definição de um conjunto de distâncias, quando p representa valores diferentes, a distância de Min pode obter outras distâncias.

Quando p=1, obtém-se a distância de Manhattan;

Quando p=2, obtém-se a distância euclidiana;

Quando p -> ∞, obtenha a distância de Chebyshev.

Entre eles, a derivação da distância de Manhattan e da distância euclidiana é relativamente simples, e a derivação da distância de Chebyshev requer o uso do conhecimento de normas.

O conteúdo da norma a seguir foi retirado da Enciclopédia Baidu - Norma .

Como mencionado acima, a dimensão e a correlação dos parâmetros característicos afetarão a distância de Min, que também afetará a distância de Manhattan, a distância euclidiana e a distância de Chebyshev.

A distância euclidiana é mais amplamente usada do que outras medidas de distância. Para ilustrar com a distância euclidiana, por exemplo, existem dois vetores A(1,10) e B(10,1000). Ao calcular a distância euclidiana de AB, podemos descobrir que a segunda dimensão tem um impacto muito maior na distância medida do que a primeira Dimensão, que é o impacto das dimensões de diferentes dimensões na medida de distância.

Se você deseja eliminar a influência da dimensão e correlação dimensional, pode executar a análise de componentes principais (PCA), extrair indicadores abrangentes, eliminar a influência da correlação dimensional e, em seguida, executar o escalonamento de recursos para eliminar a influência da dimensão e, finalmente, calcular o distância. Além disso, você pode considerar o uso da distância de Mahalanobis a ser apresentada a seguir.

distância de Mahalanobis

descrição do algoritmo

A distância de Mahalanobis (distância de Mahalanobis) foi proposta pelo estatístico indiano Mahalanobis (PC Mahalanobis), que representa a distância entre um ponto e uma distribuição. É um método eficiente para calcular a similaridade entre dois conjuntos de amostras desconhecidas. Ao contrário da distância euclidiana , ela leva em conta a conexão entre várias características (por exemplo: uma informação sobre altura trará uma informação sobre peso, pois as duas estão relacionadas), e é independente de escala (scale-invariant), isto é, independente da escala de medição.

A fórmula de distância de Mahalanobis é referenciada em https://blog.csdn.net/qq_37053885/article/details/79359427.

Existem M vetores de amostra $x_{}\sim x_{}$, a matriz de covariância é registrada como S, então a distância de Mahalanobis entre dois vetores é definida como:
$$D(A,B)=\sqrt{(A_{}-B_{}{)}^T{S}^{-1}(A_{}-B_{})}$$
Quando a matriz de covariância S é uma matriz de identidade (distribuição independente e idêntica entre cada vetor de amostra), a fórmula se torna:
$$D(A,B)=\sqrt{(A_{}-B_{}{)}^T(A_{}-B_{})}$$
Neste momento, a distância de Mahalanobis é a distância euclidiana.

Quando a matriz de covariância é uma matriz identidade, tome a distância de Mahalanobis entre o vetor A=(a1,a2,…,an) e o vetor B=(b1,b2,…,bn) como exemplo, converta o vetor em um matriz, A
= $\lfloor \begin{array}{c}{a}_{}\\ a_{}\\ ...\\ a_{}\end{array}\rfloor$和B= $\lfloor \begin{array}{c}{b}_{}\\ b_{}\\ ...\\ b_{}\end{array}\rfloor$,
a terceira fórmula para uso geral, a distância europeia recomendada:
$$\begin{array}{rl}D(A,B)& =\sqrt{(A_{}-B_{}{)}^T(A_{}-B_{})}\\ & =\sqrt{\left[\begin{array}{c}{a}_{}-b_{},a_{}-b_{},...,a_{}-b_{}\end{array}\right]\lfloor \begin{array}{c}{a}_{}-b_{}\\ a_{}-b_{}\\ ...\\ a_{}-b_{}\end{array}\rfloor }\\ & =\sqrt{({um}_{}-b_{}{)}^2+({um}_{}-b_{}{)}^2+...+({um}_{}-b_{}{)}^2}\\ & =\sqrt{\sum _{eu=1}({um}_{}-b_{}{)}^2}\end{array}$$

A conversão de um vetor em uma matriz pode ser convertida em uma matriz de linhas ou em uma matriz de colunas. Aqui, o resultado do cálculo da matriz é um valor, portanto, a primeira matriz de fatores precisa ser uma matriz de linhas e é mais apropriado converter os dois vetores A e B em uma matriz coluna.

Cenário de Aplicação

Assim como a distância euclidiana, quando a correlação entre os parâmetros característicos tem maior influência, considere usar a distância de Mahalanobis em vez da distância euclidiana.

medida de similaridade

semelhança de cosseno

descrição do algoritmo

A similaridade do cosseno, também conhecida como similaridade do cosseno, é avaliar a similaridade de dois vetores calculando o valor do cosseno do ângulo entre eles . A fórmula é a seguinte: cos ( Θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n ( A i × B i ) ∑ i = 1 n ( A i ) 2 × ∑ i = 1 n ( B i ) 2 cos(\Theta) = \frac{A \cdot B}{\esquerda \| A \direita \| \esquerda \| B \direita \|} = \frac{\sum_{i=1}^ n(A_i \times B_i)}{\sqrt{\sum_{i=1}^n(A_i)^2} \times \sqrt{\sum_{i=1}^n(B_i)^2}}
$$cos\left(\Theta \right)=\frac{A\cdot }{\Vert A\Vert \Vert B\Vert }=\frac{{\sum }_{eu=1}^{}(A_{}\times B_{}}{\sqrt{{\sum }_{eu=1}^{}(A_{}{)}^2}\times \sqrt{{\sum }_{eu=1}^{}(B_{}{)}^2}}$$
A similaridade de cosseno é comumente usada para calcular a similaridade de texto e é muito eficaz. No entanto, em alguns cenários, os resultados obtidos usando a similaridade de cosseno não são precisos, então a similaridade de cosseno modificada aparece. A fórmula é a seguinte:
$$sim(A,B)=\frac{{\sum }_{eu=1}^{}(A_{}-D_{})(B_{}-D_{}}{\sqrt{{\sum }_{eu=1}^{}(A_{}-D_{}{)}^2}\times \sqrt{{\sum }_{eu=1}^{}}(B_{}-D_{}{)}^2}$$
Entre eles $D_{}$Representa a expectativa da i-ésima dimensão (ou componente).

Para comparar a similaridade de cosseno e a similaridade de cosseno modificado, dê um exemplo de filtragem colaborativa. Supondo que a faixa de avaliação do usuário para os itens seja [1,5], existem dois usuários (U1, U2) classificando três itens (A, B, C), e a matriz de classificação é a seguinte:

Item\Usuário	U1	U2
A	1	2
B	3	4
C	3	5

O usuário U1 geralmente não dá uma pontuação alta, 1 ponto significa não gostar, 3 pontos significa gostar; o usuário U2 pontua estritamente de acordo com a nota. De acordo com a ideia de filtragem colaborativa, através da matriz de pontuação, podemos julgar que A e B, C não são semelhantes e B e C são semelhantes.

Agora calcule a similaridade do item por meio do algoritmo e obtenha o vetor do item de acordo com a matriz de pontuação: A=(1,2), B=(3,4), C=(3,5)

Calcule a similaridade do item pela similaridade do cosseno:
$$\begin{array}{rl}sim(A,B)& =\frac{1\times 3+2\times }{\sqrt{1^2+2^2}\times \sqrt{3^2+4^2}}=\frac{1}{\sqrt{5}\times \sqrt{25}}\approx 0.98386991\\ sim(A,C)& =\frac{1\times 3+2\times }{\sqrt{1^2+2^2}\times \sqrt{3^2+5^2}}=\frac{1}{\sqrt{5}\times \sqrt{34}}\approx 0.997054486\\ sim(B,C& =\frac{3\times 3+4\times }{\sqrt{3^2+4^2}\times \sqrt{3^2+5^2}}=\frac{2}{\sqrt{25}\times \sqrt{34}}\approx 0.99469179\end{array}$$
Calcule a similaridade do item modificando a similaridade do cosseno, primeiro calcule a expectativa da dimensão, ou seja, calcule o valor médio da pontuação de cada usuário:

$$\begin{array}{r}{você}_{}=\frac{1+3+}{3}\approx 2.33\\ {você}_{}=\frac{2+4+}{3}\approx 3.6\end{array}$$
Em seguida, calcule a similaridade:
$$\begin{array}{rl}sim(A,B)& =\frac{(1-2.33)\times (3-2.33)+(2-3.67)\times (4-3.67}{\sqrt{(1-2.33{)}^2+(2-3.67{)}^2}\times \sqrt{(3-2.33{)}^2+(4-3.67{)}^2}}\\ & =\frac{-1.442}{\sqrt{4.5578}\times \sqrt{0.5578}}\approx -0.904500069\\ sim(A,C)& =\frac{(1-2.33)\times (3-2.33)+(2-3.67)\times (5-3.67}{\sqrt{(1-2.33{)}^2+(2-3.67{)}^2}\times \sqrt{(3-2.33{)}^2+(5-3.67{)}^2}}\\ & =\frac{-3.112}{\sqrt{4.5578}\times \sqrt{2.2178}}\approx -0.978878245\\ sim(B,C)& =\frac{(3-2.33)\times (3-2.33)+(4-3.67)\times (5-3.67}{\sqrt{(3-2.33{)}^2+(4-3.67{)}^2}\times \sqrt{(3-2.33{)}^2+(5-3.67{)}^2}}\\ & =\frac{0.887}{\sqrt{0.5578}\times \sqrt{2.2178}}\approx 0.79820546\end{array}$$
O foco da similaridade do cosseno modificado é a correção , que é centralizar as dimensões e então calcular a similaridade do cosseno.

Na verdade, podemos centralizar A, B e C primeiro para obter A1=(-1,33,-1,67), B1=(0,67,0,33), C1=(0,67,1,33) e depois calcular a similaridade do cosseno. Na implementação real do algoritmo, essa operação passo a passo também pode ser usada para otimizar o algoritmo.

Cenário de Aplicação

Amplamente utilizado em similaridade de texto e similaridade de item em sistemas de filtragem colaborativa.

Coeficiente de correlação de Pearson

descrição do algoritmo

Em estatística , o coeficiente de correlação de Pearson (coeficiente de correlação de Pearson), também conhecido como coeficiente de correlação produto-momento de Pearson ( PPMCC ou PCCs para abreviar ), é usado para medir a relação entre duas variáveis ​​Correlação X e Y (correlação linear), com valores entre -1 e 1.

O coeficiente de correlação de Pearson entre duas variáveis ​​é definido como o quociente da covariância e desvio padrão entre as duas variáveis ​​:
$$\begin{array}{rl}p(X,Y)& =\frac{cov(X,Y}{p_{}{p}_{}}\\ & =\frac{E\left[\right(X-m_{}\left)\right(Y-m_{})}{p_{}{p}_{}}\\ & =\frac{{\sum }_{eu=1}^{}(X_{}-\bar{x})(E_{}-\bar{Y}}{\sqrt{{\sum }_{eu=1}^{}(X_{}-\bar{x}{)}^2}\sqrt{{\sum }_{eu=1}^{}(Y_{}-\bar{Y}{)}^2}}\end{array}$$
Observe que esta fórmula é muito semelhante à similaridade de cosseno modificada e, em seguida, observe a fórmula de similaridade de cosseno modificada:
$$sim(A,B)=\frac{{\sum }_{eu=1}^{}(A_{}-D_{})(B_{}-D_{}}{\sqrt{{\sum }_{eu=1}^{}(A_{}-D_{}{)}^2}\times \sqrt{{\sum }_{eu=1}^{}}(B_{}-D_{}{)}^2}$$

A diferença entre os dois pode ser entendida da seguinte forma:

A similaridade de cosseno modificada resolve a similaridade do vetor. O conjunto é considerado como um vetor, e a similaridade de cosseno modificada é centrada na mesma dimensão, ou seja, a coluna é centralizada; o coeficiente de correlação de Pearson resolve a correlação linear, e o conjunto é considerado como Para variáveis ​​contínuas positivas, o coeficiente de correlação de Pearson é centrado na mesma variável, ou seja, centrado por linha.

O seguinte é também um exemplo de filtragem colaborativa para calcular a similaridade do usuário e ilustrar o método de centralização do coeficiente de correlação de Pearson.

Ainda tomando como exemplo a matriz de pontuação, suponha que exista a seguinte matriz de pontuação:

Usuário\Item	I1	I2	I3
A	1	2	3
B	4	4	1
C	3	4	5

Obtenha as variáveis ​​A=(1,2,3), B=(4,4,1), C=(3,4,5), de acordo com a ideia de filtragem colaborativa, podemos julgar que A é semelhante para C através da matriz de pontuação, B e A, C não são semelhantes.

Cálculo esperado:
$$\begin{gathered} {você}_{}=\frac{1+2+}{3}=2 \\ {você}_{}=\frac{4+4+}{3}=3 \\ {você}_{}=\frac{3+4+}{3}=4 \end{gathered}$$

Centralize primeiro para obter novas variáveis: A1=(-1,0,1), B1=(1,1,-2), C1=(-1,0,1)

Calcule o coeficiente de correlação de Pearson:
$$\begin{array}{rl}r(A_{},B_{})& =\frac{-1\times 1+0\times 1+1\times (-2}{\sqrt{(-1)\_{}^2+0^2+1^2}\sqrt{1^2+1^2+(-2{)}^2}}=\frac{-}{\sqrt{2}\sqrt{6}}\approx -0.866025404\\ r(A_{},C_{})& =\frac{-1\times (-1)\_+0\times 0+1\times }{\sqrt{(-1)\_{}^2+0^2+1^2}\sqrt{(-1)\_{}^2+0^2+1^2}}=\frac{}{\sqrt{2}\sqrt{2}}=1\\ r(B_{},C_{}& =\frac{1\times (-1)\_+1\times 0+(-2)\times }{\sqrt{1^2+1^2+(-2{)}^2}\sqrt{(-1)\_{}^2+0^2+1^2}}=\frac{-}{\sqrt{6}\sqrt{2}}\approx -0.86602540\end{array}$$

Três principais coeficientes de correlação em estatística: coeficiente de correlação de Pearson , coeficiente de correlação de Spearman , coeficiente de correlação de Kendall .

Cenário de Aplicação

Aplicado à observação de correlação de variáveis, redução da dimensionalidade dos dados.

Similaridade de usuário que pode ser usada em sistemas de filtragem colaborativa.

Coeficiente de Jaccard

descrição do algoritmo

O índice de Jaccard, também conhecido como coeficiente de similaridade de Jaccard (coeficiente de similaridade de Jaccard), é usado para comparar a similaridade e a diferença entre conjuntos de amostras limitadas. Quanto maior o valor do coeficiente de Jaccard, maior a similaridade da amostra.

Dados dois conjuntos A, B, o coeficiente de Jaccard é definido como a razão entre o tamanho da interseção de A e B e o tamanho da união de A e B, definido da seguinte forma: J ( A , B ) = ∣ A
$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}=\frac{|A\cap B|}{|A|+|B|-|A\cap B|}$$
O intervalo de valores de J(A,B) é [0,1]. Quando os conjuntos A e B estão vazios, J(A,B) é definido como 1.

O índice relacionado ao coeficiente de Jaccard é chamado de distância de Jaccard, que é usado para descrever o grau de dissimilaridade entre os conjuntos. Quanto maior a distância de Jaccard, menor a similaridade da amostra. A fórmula é definida da seguinte forma:
$$D_{}(A,B)=1-J(A,B)=\frac{|A\cup B|-|A\cap B|}{|A\cup B|}=\frac{A\Delta }{|A\cup B|}$$
O coeficiente de Jaccard mede a similaridade de atributos binários assimétricos.

No campo da mineração de dados, muitas vezes é necessário comparar a distância entre dois objetos com atributos booleanos, e a distância Jaccard é um método comumente usado. Dados dois objetos de comparação A, B. Tanto A quanto B possuem n atributos binários, ou seja, cada atributo assume o valor {0,1}. Defina as 4 estatísticas a seguir:

$M_0$: O número de atributos cujos valores de atributo de A e B são 0 ao mesmo tempo;

$M_0$: O número de atributos cujo valor do atributo A é 0 e o valor do atributo B é 1;

$M_1$: O número de atributos cujo valor do atributo A é 1 e o valor do atributo B é 0;

$M_1$: O número de atributos cujos valores de atributo A e B são 1 ao mesmo tempo.

Conforme mostra a tabela a seguir:

A\B	0	1
0	$M_0$	$M_0$
1	$M_1$	$M_1$

Jaccard 系数：
$$J(A,B)=\frac{M_1}{M_0+M10+M11}$$
Jaccard距离：
$$D_{}(A,B)=1-J(A,B)=\frac{M_0+M_1}{M_0+M_1+M_1}$$

Cenário de Aplicação

Compare similaridade de texto para verificação e desduplicação de duplicação de texto;

Calcule a distância entre objetos, para agrupamento de dados, etc.

Também pode ser usado para calcular a similaridade de itens em um sistema de filtragem colaborativa. Em pesquisas relacionadas, a similaridade de cosseno é comumente usada em métodos de medição de similaridade baseados em sistemas de filtragem colaborativa de itens. No entanto, em muitas aplicações práticas, os dados de avaliação são muito esparsos e o cálculo da similaridade do cosseno entre os itens produzirá resultados enganosos. Aplique a medida de similaridade de Jaccard ao sistema de filtragem colaborativa baseado em itens e estabeleça o método de análise de avaliação correspondente. Comparado com o método tradicional de medição de similaridade, o método Jaccard melhora as desvantagens da similaridade de cosseno que considera apenas as avaliações do usuário e ignora outras informações, sendo especialmente adequado para dados muito esparsos.

Resumo das diferenças de métricas

Distância euclidiana e distância de Mahalanobis

A distância euclidiana será afetada pela dimensão e correlação dos parâmetros característicos, e a distância de Mahalanobis é dividida pela matriz de covariância, eliminando assim a influência da dimensão. Quando a matriz de covariância é uma matriz de identidade, a distância de Mahalanobis é a euclidiana distância.

Distância euclidiana e similaridade de cosseno

A distância euclidiana mede a distância entre dois pontos no espaço vetorial, e a similaridade do cosseno mede a diferença de direção entre dois vetores no espaço vetorial. Para um mesmo conjunto de vetores, os resultados obtidos pela distância euclidiana e pela similaridade do cosseno serão muito diferentes. Ao fazer uma seleção, é necessário julgar se a distância ou direção deve ser medida de acordo com a cena real e, em seguida, selecionar o algoritmo.

Similaridade de cosseno e coeficiente de correlação de Pearson

Em um sistema de filtragem colaborativa, a similaridade do cosseno é frequentemente usada para calcular a similaridade do item, e o coeficiente de correlação de Pearson é frequentemente usado para calcular a similaridade do usuário.

Similaridade de cosseno e coeficiente de Jaccard

Em um sistema de filtragem colaborativa, a similaridade do cosseno é a mais comumente usada para calcular a similaridade do item, mas quando a matriz de pontuação é muito esparsa, a similaridade do cosseno produzirá resultados enganosos. Neste momento, estabelecendo um método de análise de avaliação correspondente e, em seguida, combinando o coeficiente de Jaccard, o efeito da similaridade do item calculado pode ser melhor.