A idéia de design do método de dividir e conquistar é dividir um grande problema difícil de resolver diretamente nos mesmos problemas de menor escala, para que cada um possa ser dividido, dividido e governado. Se o problema original puder ser dividido em k subproblemas (1 <k≤n), e esses subproblemas puderem ser resolvidos e as soluções desses subproblemas puderem ser usadas para encontrar a solução do problema original, esse método de divisão e conquista é viável. O subproblema gerado pelo método de dividir e conquistar é geralmente um modelo menor do problema original, que fornece conveniência para o uso de técnicas recursivas.
3.1 Algoritmo recursivo A
chamada direta ou indireta do programa a suas habilidades de programação é chamada algoritmo recursivo (Recursão).
A recursão precisa ter condições de contorno, segmento recursivo direto e segmento recursivo de retorno.
- Quando as condições de contorno não forem atendidas, avance recursivamente;
- Quando as condições de contorno forem atendidas, retorne recursivamente.
- Nota: Ao usar a estratégia de recursão incremental, deve haver uma condição final de recursão clara, chamada saída de recursão, caso contrário, continuará indefinidamente (deadlock).
Desvantagens da recursão:
- A eficiência do algoritmo recursivo para resolver problemas é baixa.
- No processo de chamada recursiva, o sistema abre uma pilha para armazenar o ponto de retorno e as variáveis locais de cada camada. Muitos tempos de recursão podem facilmente causar estouro de pilha.
3.1.1 Algoritmo de sequência de Fibonacci
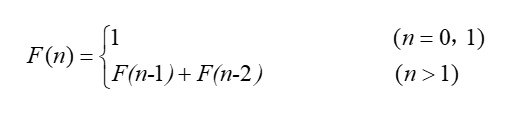
3.1 Algoritmo recursivo da sequência de Fibonacci
int fib(int n)
{
if (n<=1)
return 1;
return fib(n-1)+fib(n-2);
}A eficiência desse algoritmo é muito baixa porque a recursão é repetida muitas vezes.
Algoritmo 3.2 Algoritmo recursivo da sequência de Fibonacci
int fib[50];
void fibonacci(int n)
{
fib[0] = 1;
fib[1] = 1;
for (int i=2; i<=n; i++)
fib[i] = fib[i-1]+fib[i-2];
}3.1.2 Algoritmos para o problema completo de permutação de
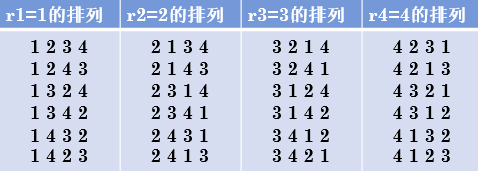
conjuntos 3.3 Recursão do problema de permutação
void Perm(int list[], int k, int m)
{
if(k==m)
{
for(int i=0;i<=m;i++)
cout<<list[i]<<" ";
cout<<endl;
}
else
for(int j=k;j<=m;j++)
{
swap(list[k],list[j]);
Perm(list,k+1,m);
swap(list[k],list[j]);
}
}3.1.3 Problema na partição
inteira O problema da partição inteira é uma das proposições clássicas no algoritmo. Representa um número inteiro positivo n como a soma de uma série de números inteiros positivos: n = n1 + n2 +… + nk (onde n1> = n2> =…> = nk> = 1, k> = 1)
Esta representação do número inteiro positivo n Isso é chamado de divisão do número inteiro positivo n. O número de diferentes divisões de um número inteiro positivo n é chamado número de divisão de um número inteiro positivo n e é indicado como p (n).
O número inteiro positivo 6 tem as 11 divisões diferentes a seguir, então p (6) = 11.
6
5 + 1
4 + 2, 4 + 1 + 1
3 + 3, 3 + 2 + 1, 3 + 1 + 1 + 1
2 + 2 + 2, 2 + 2 + 1 + 1, 2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1 + 1
algoritmo de análise de

algoritmo 3.4 algoritmo de partição do número inteiro positivo n
int split(int n,int m)
{
if(n==1||m==1)
return 1;
else if (n<m)
return split(n,n);
else if(n==m)
return split(n,n-1)+1;
else
return split(n,m-1)+split(n-m,m);
}3.2 Estratégia de
divisão e conquista A estratégia de divisão e conquista é para um problema de tamanho n. Se o problema puder ser facilmente resolvido (por exemplo, se o tamanho de n for pequeno), ele será resolvido diretamente; caso contrário, será decomposto em k subproblemas em pequena escala. Os subproblemas são independentes um do outro e têm a mesma forma que o problema original.
Resolva esses subproblemas recursivamente e, em seguida, combine as soluções de cada subproblema para obter o problema original.
3.2.1 Etapas básicas do
método de divisão e conquista O método de divisão e conquista possui três etapas em cada nível de recursão:
- Decomposição : Decomponha o problema original em vários subproblemas de menor escala, independentes um do outro e da mesma forma que o problema original;
- Solução : Se o subproblema for pequeno e fácil de ser resolvido, resolva-o diretamente; caso contrário, resolva cada subproblema recursivamente;
- Mesclar : mesclar as soluções de cada subproblema no problema original.
Algoritmo 3.5 Padrão de design do algoritmo da estratégia de dividir e conquistar
Divide_and_Conquer(P)
{
if (|P|<=n0 )
return adhoc(P);
divide P into smaller substances P1,P2,…,Pk;
for (i=1; i<=k; k++)
yi=Divide-and-Conquer(Pi)
Return merge(y1,y2,…,yk)
}Ao projetar algoritmos usando o método de dividir e conquistar, é melhor tornar a escala dos subproblemas aproximadamente a mesma. Se dividido em k subproblemas de tamanho igual, muitos problemas podem levar k = 2. Essa abordagem de tornar os subproblemas aproximadamente iguais é derivada da idéia de um subproblema de balanceamento, quase sempre melhor do que a prática de subproblemas desiguais.
3.2.2 Condições aplicáveis do
método de divisão e conquista Os problemas que o método de divisão e conquista podem resolver geralmente têm as seguintes características:
- Esse problema pode ser facilmente resolvido, reduzindo a escala até um certo ponto;
- O problema pode ser decomposto em vários problemas idênticos de menor escala, ou seja, o problema tem a propriedade ideal de subestrutura;
- As soluções dos subproblemas decompostos por esse problema podem ser combinadas na solução desse problema;
- Os subproblemas decompostos por esse problema são independentes um do outro, ou seja, não há subproblema comum entre os subproblemas.
3.2.4 Programação do round-robin
Descrição do problema: Existem n = 2k atletas para jogar um torneio round-robin.
Agora precisamos criar uma programação de jogos que atenda aos seguintes requisitos:
- Cada jogador deve competir com outros jogadores n-1 uma vez;
- Cada jogador pode competir apenas uma vez por dia;
- O jogo round robin termina em n-1 dias.
Projete a programação do jogo como uma tabela com n linhas e n-1 colunas de acordo com este requisito. Na i-ésima linha e j-ésima coluna da tabela, preencha o jogador que o i-ésimo jogador conheceu no j-ésimo dia, em que 1≤i≤n, 1≤j≤n-1.
void Table(int k)
{
int i, r;
int n = 1 << k;
for (i=0; i<n; i++)
a[0][i] = i + 1;
for (r=1; r<n; r<<=1)
for (i=0; i<n; i+=2*r)
{
Copy(r, r + i, 0, i, r);
Copy(r, i, 0, r + i, r);
}
}Realize a cópia da matriz quadrada
//源方阵的左上角顶点坐标(fromx, fromy),行列数为r
//目标方阵的左上角顶点坐标(tox, toy),行列数为r
void Copy(int tox, int toy, int fromx, int fromy, int r)
{
for (int i=0; i<r; i++)
for (int j=0; j<r; j++)
a[tox+i][toy+j] = a[fromx+i][fromy+j];
}3.2.6 Problema de seleção
Para uma determinada matriz de n elementos a [0: n-1], é necessário encontrar o k-ésimo elemento menor.
Entrada Existem
vários conjuntos de casos de teste.
Existem 2 linhas para cada caso de teste, a primeira linha é números inteiros nek (1≤k <n≤1000) e a segunda linha é n números inteiros.
Emita
o k-ésimo elemento menor.
Use a ideia do algoritmo de classificação rápida para resolver o problema de seleção.
Depois de lembrar de uma classificação rápida, o número de elementos no subconjunto esquerdo é decomposto para ser nulo, então o problema de seleção pode ser uma das seguintes situações:
- nleft = k ﹣ 1, então os dados do limite são a resposta para a pergunta de seleção.
- nleft> k ﹣ 1, a resposta para a pergunta selecionada continua sendo encontrada no subconjunto esquerdo e o tamanho da pergunta fica menor.
- nleft <k ﹣ 1, a resposta para a pergunta de seleção continua sendo encontrada no subconjunto direito, a questão passa a selecionar o menor número de k-nleft-1 e a escala da pergunta fica menor.
Algoritmo 3.9 Algoritmo para encontrar o k-ésimo elemento usando uma estratégia de dividir e conquistar
int select(int left,int right,int k)
{
if(left>=right)
return a[left];
int i=left;
int j=right+1;
int pivot=a[left];
while(true)
{
do{
i=i+1;
}while(a[i]<pivot);
do{
j=j-1;
}while(a[j]>pivot);
if(i>=j)
break;
swap(a[i],a[j]);
}
if(j-left+1==k)
return pivot;
a[left]=a[j];
a[j]=pivot;
if(j-left+1<k)
return select(j+1,right,k-j+left-1);
else
return select(left,j-1,k);
}3.2.7 Problema no oleoduto
Uma empresa de petróleo planeja construir um oleoduto principal de leste a oeste. O oleoduto passará por um campo de petróleo com n poços de petróleo. De cada poço, um oleoduto deve ser conectado ao oleoduto principal ao longo da rota mais curta (ou sul ou norte).
Se as posições de n poços de petróleo são dadas, ou seja, suas coordenadas x (leste-oeste) e coordenadas y (norte-sul), como determinar a posição ideal do oleoduto principal, mesmo que a soma do comprimento do oleoduto de cada poço até o oleoduto principal seja a menor. Localização?
Dadas as posições de n poços de petróleo, programe e calcule a soma do comprimento mínimo do oleoduto de cada poço até o oleoduto principal.
A
linha de entrada 1 é um número inteiro n que representa o número de poços de petróleo (1≤n≤10 000). As próximas n linhas são as posições dos poços de petróleo, com dois números inteiros x e y por linha (- 10.000≤x, y≤10.000).
Saída
A soma do comprimento mínimo do oleoduto de cada poço ao oleoduto principal.
Suponha que as posições de n poços de petróleo sejam pi = (xi, yi), i = 1 ~ n. Como o oleoduto principal é leste-oeste , a coordenada y do seu eixo principal pode ser usada para determinar exclusivamente sua posição. A posição ideal y do pipeline principal deve atender: a
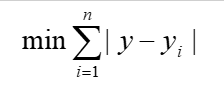
partir do teorema da mediana, y é a mediana.
Algoritmo 1: classifique a matriz a (geralmente em ordem crescente), pegue o elemento do meio
int n;
int x;
int a[1000];
cin>>n;
for(int k=0;k<n;k++)
cin>>x>>a[k];
sort(a,a+n);
int min=0;
for(int i=0;i<n;i++)
min += (int)fabs(a[i]-a[n/2]);
cout<<min<<endl;Algoritmo 2: Use a estratégia de dividir e conquistar para encontrar a mediana
int n;
int x;
int a[1000];
cin>>n;
for (int i=0; i<n; i++)
cin>>x>>a[i];
int y = select(0, n-1, n/2);
int min=0;
for(int i=0;i<n;i++)
min += (int)fabs(a[i]-y);
cout<<min<<endl;3.2.8 Problema no conjunto de meio número
Dado um número natural n, começando em n, os números no conjunto de meio número definido (n) podem ser gerados sucessivamente, como segue.
(1) n conjunto (n);
(2) Adicione um número natural à esquerda de n, mas o número natural não pode exceder a metade do número adicionado recentemente;
(3) Processe de acordo com esta regra até que nenhum número natural possa ser adicionado.
Por exemplo, defina (6) = {6, 16, 26, 126, 36, 136}.
Existem 6 elementos no conjunto (6).
Observe que o meio conjunto é um conjunto múltiplo .
Para um determinado número natural n, programe para calcular o número de elementos no conjunto (n) do meio conjunto.
Se o número de elementos no conjunto (n) for f (n), haverá obviamente:
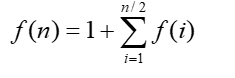
Algoritmo 3.12 Algoritmo recursivo para calcular o problema do conjunto de meio número
int comp(int n)
{
int ans=1;
if (n>1)
for(int i=1;i<=n/2;i++)
ans+=comp(i);
return ans;
}Algoritmo 3.13 Algoritmo recursivo para calcular a pesquisa de problemas-memória de conjunto de meio número
int a[1001];
int comp(int n)
{
int ans=1;
if(a[n]>0)
return a[n];
for(int i=1;i<=n/2;i++)
ans+=comp(i);
a[n]=ans;
return ans;
}