背景
機械学習を学習の考え方の基礎として。
1.概要
アプリケーションの広い範囲で機械学習で勾配降下(勾配降下)は、オンラインまたは回帰ロジスティック回帰するかどうか、その主な目的は、反復的に最小に最小目的関数、または収束を見つけることです。
シーンからのこの記事では、下り坂数学的に、なぜ利用勾配を説明する最初の勾配降下アルゴリズムの基本的な考え方提唱し、起動し、勾配降下アルゴリズムの原理を説明、勾配降下アルゴリズムの簡単な例の最終的な実現!
2.勾配降下アルゴリズム
2.1シナリオは想定してい
勾配降下法の基本的な考え方は、下り坂のコースに似ています。
そのように、Aのシナリオを想定します。山の中に閉じ込められた男が、我々は(谷である山、の最下点を見つけるために)山を降りてくる必要があります。しかし、この時の低可視性が得られ、大きな丘の霧が、あるため、道を決めることができない、あなたは道を見つけるためにステップによってそれらのステップを中心に情報を使用する必要があります。今回は、山のダウンそれらを助けるために勾配降下アルゴリズムを使用することができます。それを行うにはどのように、この位置で最も急な場所を見つけることで、参照としての彼の現在の位置までのすべての最初の、最も急な場所を見つけ、その後、方向を下げるに向けた一歩を踏み出す、その後、基準に現在位置を続け、散歩あまりにも、共感山を、今回はそれが勾配上昇アルゴリズムとなり、最終的には最低点に達するまで

2.2勾配降下
山ダウンと非常によく似たシーンの勾配降下の基本的なプロセス。
まず第一に、我々は微分可能関数。この関数は、山を表しています。私たちの目標は、山のベースである、この関数の最小値を見つけることです。シナリオは、最速の方法は、急な現在位置と向きダウンほとんどを見つけ、その後、この方向に沿って下る、することである前にあることを前提とした機能に対応する、ポイントは勾配を見つけることです、勾配の反対方向に向かって、その後、およびあなたは、関数の値で最速の下落を作ることができます!勾配の方向が最速の方向の変化の関数であるので(後で説明します)
私たちは、このメソッドを再利用するので、繰り返し勾配を打つ、そして最終的に我々がダウンしている処理と同様である局所的最小値に到達することができ、。ストライキは、測定手段の方向にシーンで最急勾配方向を決定します。なぜ、勾配の方向が最も急勾配の方向ですか?次に、我々は差動で起動します。
2.2.1 微分
差動の意義を見ると、あなたは別の視点を持つことができ、二つの最も一般的なのは、次のとおりです。
- 画像機能、点における接線の傾き
- 機能の変化率
分化のいくつかの例:
1つだけ可変差動変数、関数
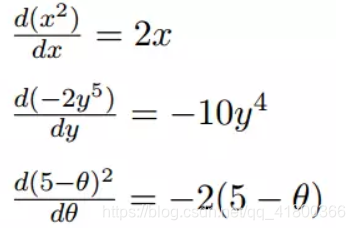
微分2.多変数関数の各変数について別々に、すなわち複数の変数は、微分
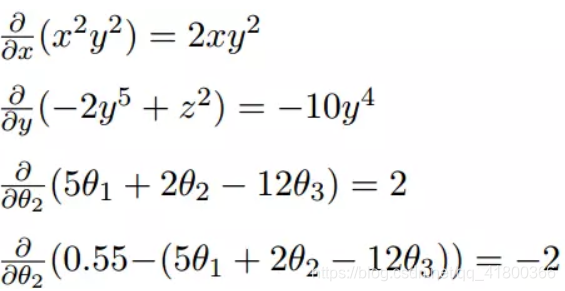
2.2.2グラデーション
多変量一般化勾配は、実際誘導体です。
次の例:
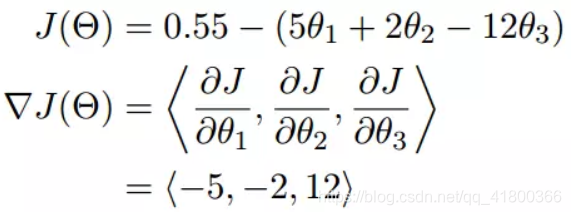
我々は次に、カンマで区切られた、勾配が各可変差動について別々であることが確認でき、勾配は、<>、実際には、勾配ベクトル命令を、それらを含むあります。
微積分勾配が非常に重要な概念である、以前に勾配を意味言及
- 単変量関数では、勾配は、所与の点での正接関数の傾きを表す、実際微分関数であります
- 多変数関数では、勾配はベクトルであり、ベクトルの方向を有し、勾配の方向は、最速の方向に固定小数点機能の上昇を指摘しました
这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
2.3 数学解释
首先给出数学公式:

此公式的意义是:J是关于Θ的一个函数,我们当前所处的位置为Θ0点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是α,走完这个段步长,就到达了Θ1这个点!
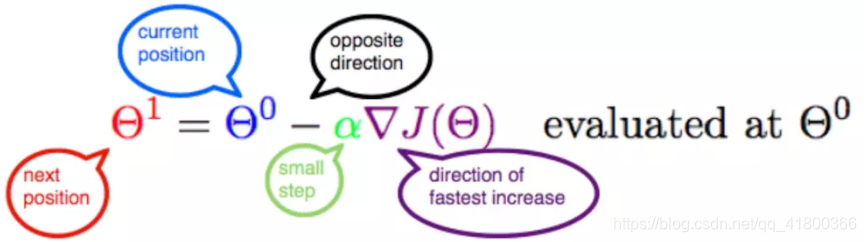
2.3.1 α
α在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,以保证不要步子跨的太大扯着蛋,哈哈,其实就是不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点!
2.3.2 梯度要乘以一个负号
梯度前加一个负号,就意味着朝着梯度相反的方向前进!我们在前文提到,梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号;那么如果时上坡,也就是梯度上升算法,当然就不需要添加负号了。
3. 实例
我们已经基本了解了梯度下降算法的计算过程,那么我们就来看几个梯度下降算法的小实例,首先从单变量的函数开始,然后介绍多变量的函数。
3.1 单变量函数的梯度下降
我们假设有一个单变量的函数
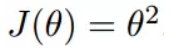
函数的微分,直接求导就可以得到
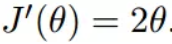
初始化,也就是起点,起点可以随意的设置,这里设置为1

学习率也可以随意的设置,这里设置为0.4
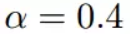
根据梯度下降的计算公式

我们开始进行梯度下降的迭代计算过程:
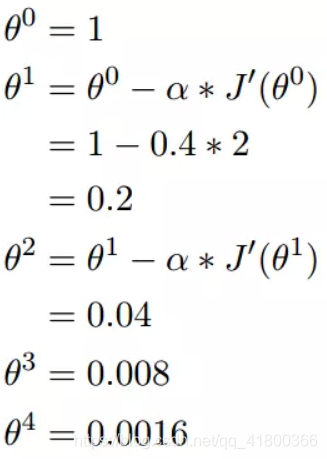
如图,经过四次的运算,也就是走了四步,基本就抵达了函数的最低点,也就是山底
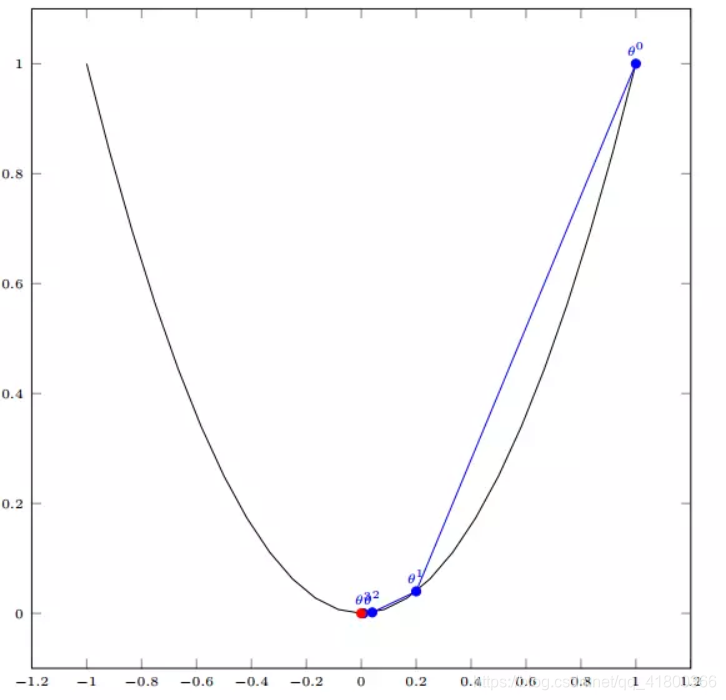
3.2 多变量函数的梯度下降
我们假设有一个目标函数
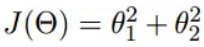
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0,0)点。但是接下来,我们会从梯度下降算法开始一步步计算到这个最小值!
我们假设初始的起点为:
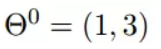
初始的学习率为:
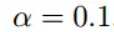
函数的梯度为:
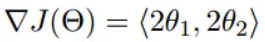
进行多次迭代:

我们发现,已经基本靠近函数的最小值点
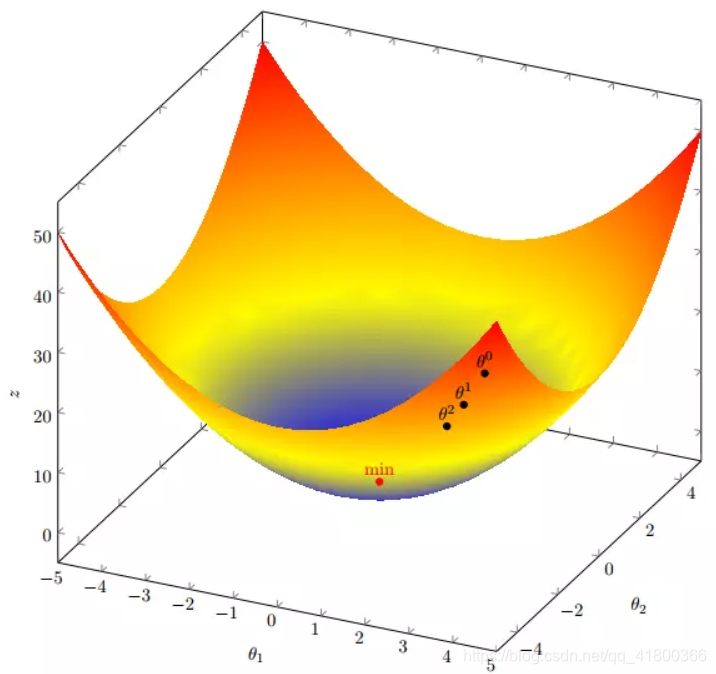
4. 代码实现
4. 1 场景分析
下面我们将用python实现一个简单的梯度下降算法。场景是一个简单的线性回归的例子:假设现在我们有一系列的点,如下图所示:
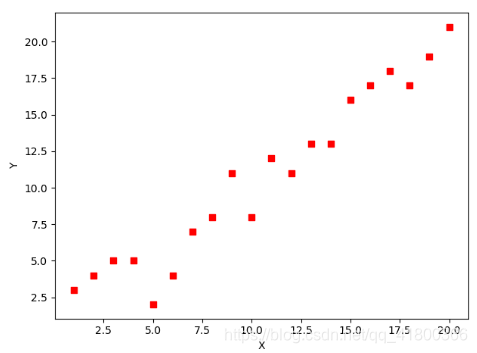
我们将用梯度下降法来拟合出这条直线!
首先,我们需要定义一个代价函数,在此我们选用均方误差代价函数(也称平方误差代价函数)
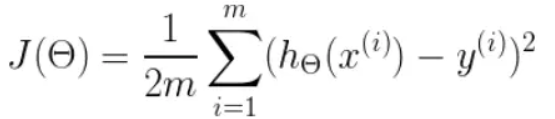
此公式中
- m是数据集中数据点的个数,也就是样本数
- ½是一个常量,这样是为了在求梯度的时候,二次方乘下来的2就和这里的½抵消了,自然就没有多余的常数系数,方便后续的计算,同时对结果不会有影响
- y 是数据集中每个点的真实y坐标的值,也就是类标签
- h 是我们的预测函数(假设函数),根据每一个输入x,根据Θ 计算得到预测的y值,即
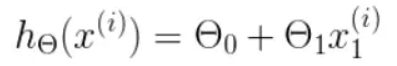
我们可以根据代价函数看到,代价函数中的变量有两个,所以是一个多变量的梯度下降问题,求解出代价函数的梯度,也就是分别对两个变量进行微分
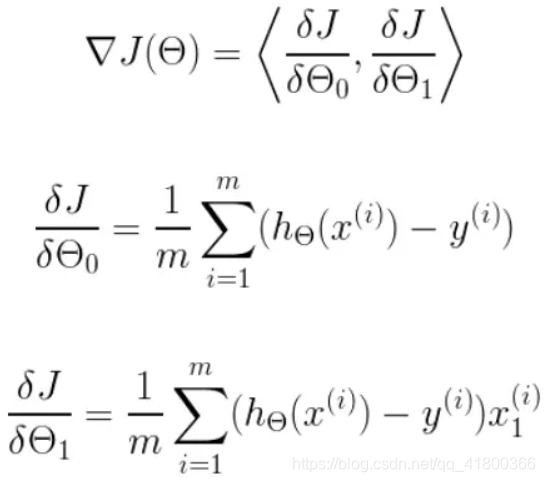
明确了代价函数和梯度,以及预测的函数形式。我们就可以开始编写代码了。但在这之前,需要说明一点,就是为了方便代码的编写,我们会将所有的公式都转换为矩阵的形式,python中计算矩阵是非常方便的,同时代码也会变得非常的简洁。
为了转换为矩阵的计算,我们观察到预测函数的形式
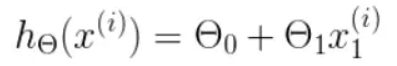
我们有两个变量,为了对这个公式进行矩阵化,我们可以给每一个点x增加一维,这一维的值固定为1,这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算
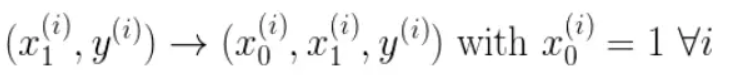
然后我们将代价函数和梯度转化为矩阵向量相乘的形式

4. 2 代码
首先,我们需要定义数据集和学习率
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time : 2019/1/21 21:06
# @Author : Arrow and Bullet
# @FileName: gradient_descent.py
# @Software: PyCharm
# @Blog :https://blog.csdn.net/qq_41800366
from numpy import *
# 数据集大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1)) # 生成一个m行1列的向量,也就是x0,全是1
X1 = arange(1, m+1).reshape(m, 1) # 生成一个m行1列的向量,也就是x1,从1到m
X = hstack((X0, X1)) # 按照列堆叠形成数组,其实就是样本数据
# 对应的y坐标
y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# 学习率
alpha = 0.01
1234567891011121314151617181920212223接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度
# 定义代价函数
def cost_function(theta, X, Y):
diff = dot(X, theta) - Y # dot() 数组需要像矩阵那样相乘,就需要用到dot()
return (1/(2*m)) * dot(diff.transpose(), diff)
# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
diff = dot(X, theta) - Y
return (1/m) * dot(X.transpose(), diff)
12345678910最后就是算法的核心部分,梯度下降迭代计算
# 梯度下降迭代
def gradient_descent(X, Y, alpha):
theta = array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, Y)
while not all(abs(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, Y)
return theta
optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])
12345678910111213当梯度小于1e-5时,说明已经进入了比较平滑的状态,类似于山谷的状态,这时候再继续迭代效果也不大了,所以这个时候可以退出循环!
运行代码,计算得到的结果如下:
print('optimal:', optimal) # 结果 [[0.51583286][0.96992163]]
print('cost function:', cost_function(optimal, X, Y)[0][0]) # 1.014962406233101
12通过matplotlib画出图像,
# 根据数据画出对应的图像
def plot(X, Y, theta):
import matplotlib.pyplot as plt
ax = plt.subplot(111) # 这是我改的
ax.scatter(X, Y, s=30, c="red", marker="s")
plt.xlabel("X")
plt.ylabel("Y")
x = arange(0, 21, 0.2) # x的范围
y = theta[0] + theta[1]*x
ax.plot(x, y)
plt.show()
plot(X1, Y, optimal)
1234567891011121314所拟合出的直线如下
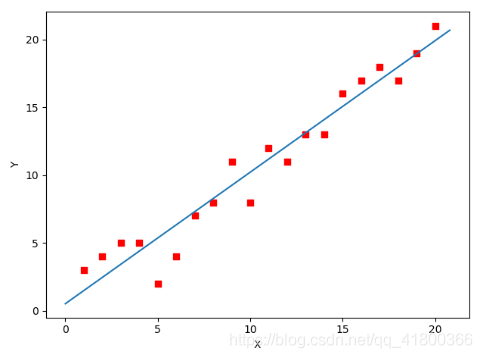
全部代码如下,大家有兴趣的可以复制下来跑一下看一下结果:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time : 2019/1/21 21:06
# @Author : Arrow and Bullet
# @FileName: gradient_descent.py
# @Software: PyCharm
# @Blog :https://blog.csdn.net/qq_41800366
from numpy import *
# 数据集大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1)) # 生成一个m行1列的向量,也就是x0,全是1
X1 = arange(1, m+1).reshape(m, 1) # 生成一个m行1列的向量,也就是x1,从1到m
X = hstack((X0, X1)) # 按照列堆叠形成数组,其实就是样本数据
# 对应的y坐标
Y = array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# 学习率
alpha = 0.01
# 定义代价函数
def cost_function(theta, X, Y):
diff = dot(X, theta) - Y # dot() 数组需要像矩阵那样相乘,就需要用到dot()
return (1/(2*m)) * dot(diff.transpose(), diff)
# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
diff = dot(X, theta) - Y
return (1/m) * dot(X.transpose(), diff)
# 梯度下降迭代
def gradient_descent(X, Y, alpha):
theta = array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, Y)
while not all(abs(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, Y)
return theta
optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])
# 根据数据画出对应的图像
def plot(X, Y, theta):
import matplotlib.pyplot as plt
ax = plt.subplot(111) # 这是我改的
ax.scatter(X, Y, s=30, c="red", marker="s")
plt.xlabel("X")
plt.ylabel("Y")
x = arange(0, 21, 0.2) # x的范围
y = theta[0] + theta[1]*x
ax.plot(x, y)
plt.show()
plot(X1, Y, optimal)
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465665. 小结
この時点で、それは基本的に勾配降下アルゴリズムの基本的な考え方やプロセスの上に導入し、Pythonの実装で勾配降下アルゴリズムの簡単なケースは、直線に合わせて!
最後に、我々は、資料の冒頭シーンに戻るという仮説を提案した:
このダウンの人々が実際に表しているバックプロパゲーションアルゴリズムを実際にアルゴリズムはパラメータΘ、最も急な山の現在のポイントを探していた表しパスダウン、方向は、実際の勾配の方向におけるこの時点でのコスト関数であり、シーンの観察ツールは、最急勾配方向によって使用される差動。次観測するまでの時間は、私たちは学習率αアルゴリズムが定義されているということです。
私たちはよくやった、対応するシーンの仮定および勾配降下アルゴリズムを見ることができます!
先輩から、この記事の内容のほとんどは、その共有のための感謝!ありがとうございます!