バブルソート：（A）を学習するアルゴリズムをソート

すなわち、いわゆるデータのセットに特定の規則に従ってソートが配列されています。ソートアルゴリズムの正式な定義は次のように無秩序配列のセットがありましょう $\ {X_1、X_2、...、x_nに関する\}$ 、そして機能がある $f（x）が$ 任意の新しいについて得られた、位置一連の要素の配列を調整した後、そのような配列は満足 $0 \ I \ jの\ nは$ です $F（X_I）\ F（X - jが）$ （昇順）または $F（X_I）\ GE F（X - jが）$ （降順）。異なるデータソースの異なる特性のために、人々は時間の複雑さや最適化のスペースの複雑さのために、異なるソートアルゴリズムを設計します。バブルソート、挿入ソート、クイックソート、バケットソートアルゴリズム：アルゴリズムをソート共通。様々なソートアルゴリズムの次の原則を概説し、その強みと弱みを分析しています。（以下、ソートアルゴリズムの説明では、データが昇順に配置されているものとします）。

バブルソート

二つの隣接する要素の大きさの比較、比較結果に応じて昇順に2つの要素を、徐々に後退し、端まで移動：アルゴリズムのステップをバブリングすることは以下の通りです。図1は、各車輪のソート処理に示した処理アルゴリズムをバブリング、すなわち、Iは、i番目の最大の要素は、アレイ内の最大の現在の位置に移動されます。ソート処理の各ラウンドでは、ソートされた配列の長さの右側には、最終的にソートされた順序になり、全体のシーケンスを作り、成長を続けています。完全なバブルソート・プロセスは以下の通り：

バブルソートアルゴリズムの実装方法

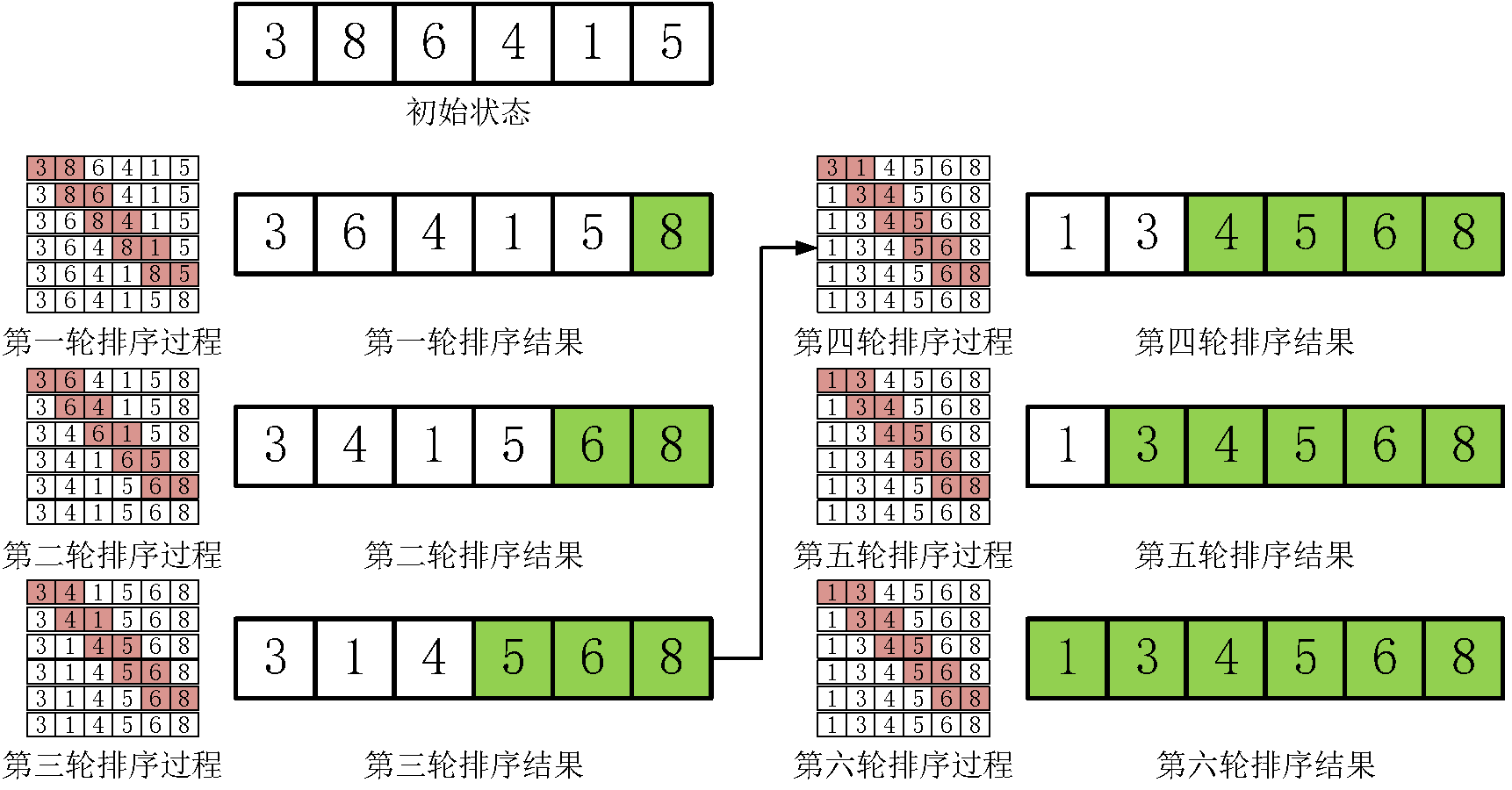
図1バブルソートのプロセスを完了します

達成するための最も基本的なバブルソートアルゴリズム

次のように図1に記載された方法は、基本的なPythonコードバブルソートアルゴリズムが実装されています。

[ソースコード言語= 'Pythonのpadlinenumbers = '真']
	デフバブルソート（データ：リスト[INT]） - >一覧[INT]：
		長さ= lenは（データ）
		Iの範囲内（0、長さ）のために：
			範囲内のjについて（0、長さ -  1）：
				もしデータ[J]>データ[J + 1]：
					TMP =データ[J]
					データ[J] =データ[J + 1]
					データ[J + 1] = TMP
		return data
[/sourcecode]

对优化后的代码分析可知，一共需要进行 $N$ 轮的排序，每一轮的排序中都需要进行 $N-1$ 次的大小比较，因此该算法的算法复杂度为 $O(n^2)$ ，空间复杂度为 $1$ 。

针对每轮比较次数的效率优化

通过对图1的观察，第1轮排序完成后，最右侧的1个元素是一个已完成排序的序列，在第2轮的排序过程中，最后1次的比较没有发生顺序的改变；第2轮排序完成后，最右侧的2个元素是一个已完成排序的序列，在第3轮的排序过程中，最后2次的比较没有发生顺序的改变。第 $I$ 轮排序完成后，最右侧的 $I$ 个元素是一个已完成排序的序列，在第 $I + 1$ 轮的排序过程中，最后 $I$ 次的比较没有发生顺序的改变。根据这个特点，我们可以对每一轮的排序过程中需要比较的次数进行优化。代码如下：

def bubbleSort(data:List[int])->List[int]:
            length = len(data)
            for i in range(0, length):
                for j in range (0, length - i - 1):
                    if data[j] > data[j + 1]:
                        tmp = data[j] data[j] = data[j+1] data[j+1] = tmp return data

在进行优化之后，可以发现在每一轮的排序过程中需要比较的元素的数量得到了优化，在第 $I$ 轮中排序中进行了 $I-1$ 次大小比较，因此在整个排序过程中，一共需要进行 $\ sum_ {1} ^ {n}は（I-1）$ 次比较运算，算法复杂度为 $O(n^2)$ ，空间复杂度为 $1$ 。

针对算法终止条件的效率优化

另外，还可以对冒泡排序算法的终止条件进行优化。我们对图1进行观察，发现从第3轮开始，序列的顺序已经达到排序完成的状态，此后序列中元素的相对位置不再发生改变，因此我们可以根据此对排序的终止条件的判断进行优化。代码如下：

    def bubbleSort(data:List[int])->List[int]):
            length = len(data)
            changed = 0
            for i in range(0, length):
                for j in range (0, length - i - 1):
                    if data[j] > data[j + 1]: tmp = data[j] data[j] = data[j+1] data[j+1] = tmp changed = 1 if changed == 0: return data return data

在进行优化之后，可以发现排序算法可能提前终止排序状态。考虑最好的情况，序列的顺序本来就是排列好的，那么需要进行一轮排序来进行确认，一共需要进行 $N-1$ 次排序，因此在最好的情况下算法的时间复杂度为 $O(n)$ ，空间复杂度为 $1$ ；在最差的情况下，一共需要进行 $\ sum_ {1} ^ {n}は（I-1）$ 次比较运算，算法复杂度为 $O(n^2)$ ，空间复杂度为 $1$ 。

鸡尾酒排序

鸡尾酒排序又称为双向冒泡排序，是冒泡排序的一个变种算法，可以在某些情况下减少算法的比较次数。鸡尾酒排序算法的过程如图2所示：

カクテルソートアルゴリズムの実装方法

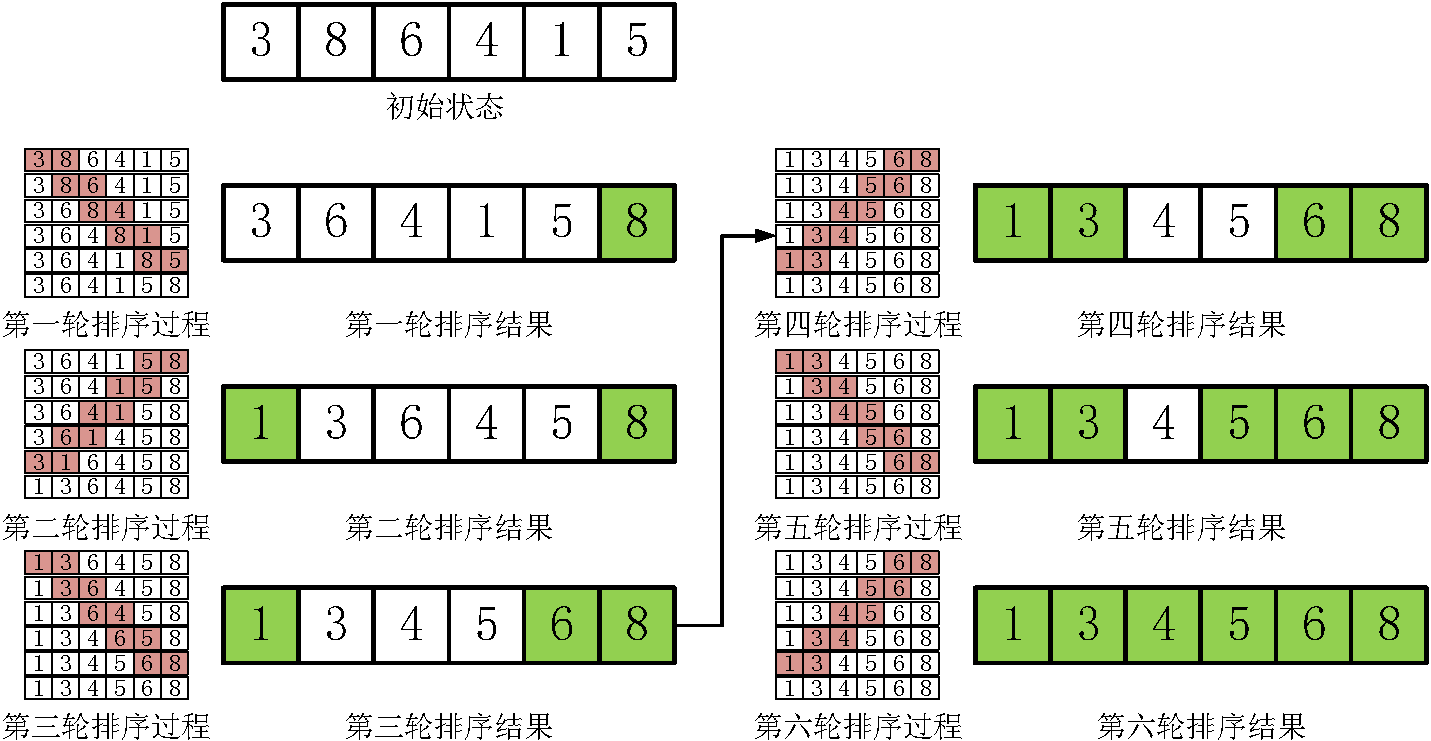
图2 鸡尾酒排序算法的执行过程

对图2观察可知，利用鸡尾酒排序在第三轮的时候，序列就已经达到了排序完成的状态。比普通的冒泡排序算法快了一轮，下面分析为什么会比冒泡算法快一轮的原因。在冒泡算法过程中，元素单一的从一侧按照从小到大的顺序被移动到另一侧。但是如果假设有这样一种情况，即序列的左侧的大部分元素的相对顺序都是排好的，只有右侧部分元素的顺序不对，那么此时鸡尾酒排序相对于冒泡排序就会有极大的优势。极端一点的例子，如：序列 $[2,3,4,5,1]$ ,如果按照冒泡排序来进行，那么需要进行4轮排序，如果按照鸡尾酒排序的算法来排序则只需要2轮排序。但是对于某些极端情况，如序列 $[5,4,3,2,1]$ ，冒泡排序和鸡尾酒排序都需要进行4轮排序。

鸡尾酒排序算法的Python代码如下（以下代码已经针对每轮的比较次数和算法终止条件进行了优化）:

    def cocktailsort(data:List[int])->List[int]):
            start = 0
            end = len(data)
            changed = 0
            while start != end: Iの範囲内（データ）（LEN、開始- 1 ）：もしデータ[I]>データ[I + 1 ]：TMP = DATA [i]はデータ[I] =データ[I + 1 ]データ[I + 1 ] = = 1枚のプリント変更TMP 変更==場合（データ）のリターン：0 データが開始= 1 +開始=変更-範囲（1、0、-1最後にI 0 データであれば、[I] <データ[I：） - 1 ]：TMP = DATA [i]はデータ[I] =データ[I - 1 ]データ[I - 1] = tmpに変更= 1つの印刷（データ）==変更された場合0：リターンデータエンド=エンド- 1リターンデータ