ディレクトリ
リニアふるいです
\(CSPの\)月未満。
私は、彼らが線形ふるいではないことがわかり、\(mdzz \) 。(
試したことのないコード、注意してご使用ください)
for(int i=2;i<=n;++i) {
if(!vis[i]) pri[++cnt]=i;
for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
vis[i*pri[j]]=1;
if(i%pri[j]==0) break;
}
}それだけ選別最小の素数になります。
\は、(N = P_1 ^ {K_1
} * P_2 ^ {K_2} ...... p_x ^ {k_x} \) 列挙\(私は\)される(\ FRAC {n}は{\
\ P_1を}) 場合(N- \を\します%PRI [j] == 0 \ ) それが列挙意味\(PRI [J] * iが \) 最小品質係数の境界。
そして、さらに\(PRI [J] \)よりも高くなります(私は\)\、もちろん、小さな素因数の内側ではありません。
未満のすべての素因数の前に\(Iは\) 、当然のことながら、ラインを素因数を。
\(N \%PRI [j ] == 0 \)は、 時間に正確に等しいです。
乗法機能を簡単に見つけることができる、あなただけの必要癌の単純な分類は十分に議論しました。
メビウス関数を求めて
\ [\ MU(X)= \左\ {\開始{整列}&1&N = 1 \\&(-1)^ K&N = P_1 * P_2 ... p_k \\&0&N =他人\端{整列} \右。\]
mu[1]=1;
for(int i=2;i<=n;++i) {
if(!vis[i]) {
pri[++cnt]=i;
mu[i]=-1;
}
for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
vis[i*pri[j]]=1;
if(i%pri[j]==0) {
mu[i*pri[j]]=0;
break;
} else mu[i*pri[j]]=-mu[i];
}
}これらの
\ [\ sum_ {D | N
}ミュー\(D)= \左\ {\開始{}&1&N = 1 \\&0整列&N> 1つの\端{整列} \ \右。] 2定理ハン証明書
\(\ sum_ I = {0} ^ {K}( - 1)kC_k ^ I ^ \) 。
オイラー機能
\(\ PHI(N)\ ) と\(N \)数は比較的素数を
ノックする気にする前に書かれました。

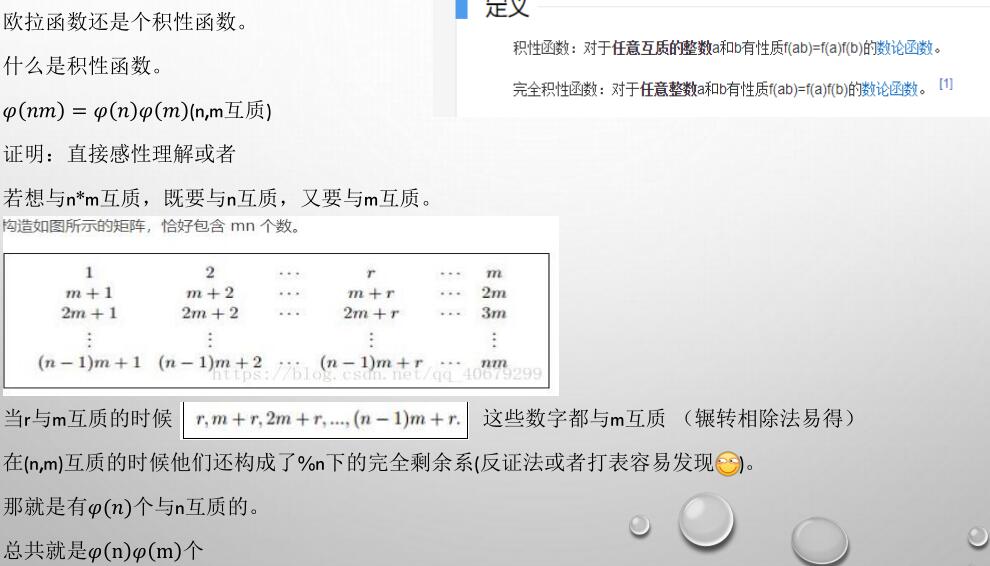

主に使用してふるい\(N * \ FRAC {p_1-1 } {P_1} ... \ FRAC {p_k-1} {p_kを} \)
phi[1]=1;
for(int i=2;i<=n;++i) {
if(!vis[i]) {
pri[++cnt]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
vis[i*pri[j]]=1;
if(i%pri[j]==0) {
phi[i*pri[j]]=phi[i]*pri[j];
break;
} else phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
}\ [\ sum_ {D | N
} \ PHI(D)= N \] 私たちは考えていない、許しません。
除数の数
もし\(P_1 = X ^ {^ {P_2のC_1とC_2}} ... {C_K} P_K ^ \) 、次いで\(D(X)=( 1 + C_1)(1 + C_2)...(1+ C_K)\)
スクリーンプロセスは、我々は記録\(NUMを(X)\)を表し\(X \)最小品質係数の数、すなわち\(C_1および\) 。
その後、\(XJB \)転送
for(int i=2;i<=n;++i) {
if(!vis[i]) {
pri[++cnt]=i;
num[i]=1;
d[i]=2;
}
for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
vis[i*pri[j]]=1;
if(i%pri[j]==0) {
num[i*pri[j]]=num[i]+1;
d[i*pri[j]]=d[i]/(num[i]+1)*(num[i*pri[j]]+1);
break;
} else {
num[i*pri[j]]=1;
d[i*pri[j]]=d[i]*2;
}
}
}約数の数
私たちは、SD(i)はIの約数を表している設定しました。
\(SD(N)=(
1 + P_1 + ... + P_1 ^ {R_1})*(1 + P_2 + ... + P_2 ^ {R_2})* ... *(1 + p_k ... + p_k ^ {r_k})\) 、等事のように列数の違い。
この時間は、我々は1がされていることを最小の素因数を記録する必要があります\((1 + p_x + p_x ^ 2 + ... + p_x R_1 ^ {})\) 、彼を呼ばれる\(NUM(i)が\) 。設定可能SD(i)と私は除数を示しています。提供される
:(a)に示すように、現在の数が素数である
\(SD(I)= I + 1が\)
\(NUM(I)= I + 1 \は。)
(ii)は、現在の素数のモジュロ列挙は0に等しくありません\((i *がプライム[jは ])\) ではないもともと\((プライム[J]) \) この1、プラス利用できるの後、このいずれかを:\(SD(i *が総理[J]) = SD(I)* SD(プライム[J])\)\(NUM(Iプライム[J]を*)= 1 +プライム[J] \) 0質量等しい列挙(III)、現在のカウントモジュロ\ (SD(プライム* I [J])= SD(I)/ NUM(I)*(NUM(I)*プライム[J] + +1)\)\(NUM(プライム* I [J])を(NUMを= ⅰ)*プライム[J] +1 \)
sd[1]=1;
for(int i=2;i<=n;++i) {
if(!vis[i]) {
pri[++cnt]=i;
num[i]=sd[i]=i+1;
}
for(int j=1;j<=cnt&&i*pri[j]<=n;++j) {
vis[i*pri[j]]=1;
if(i%pri[j]==0) {
sd[i*pri[j]]=sd[i]/num[i]*(num[i]*pri[j]+1);
num[i*pri[j]]=num[i]*pri[j]+1;
break;
} else {
sd[i*pri[j]]=sd[i]*sd[pri[j]];
num[i*pri[j]]=pri[j]+1;
}
}
}