目次
i を選択: 前のレイヤーの値が上書きされないように、右下隅は左上隅に依存します。
i は選択しないでください: dp[i][v]=dp[i-1][v] 同じ列は影響を受けません
最小：dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i])
組み合わせの数: dp[j] += dp[j - nums[i]];
i を選択: 右側は左側に依存します。同じレイヤーの値が使用されます。左側を最初に生成する必要があります。
i は選択しないでください: dp[i][v]=...dp[i-1][v] 同じ列は影響を受けません
オプションの数: dp[i] += dp[i - nums[j]]
サブシーケンス: dp[i] は添え字 i - 1/i で終わります (相対的な順序を維持します)
強盗: サブセット + 最良の値 + 連続して盗むことはできません
欲張り：左の最小値と右の最大値をとり、その差が最大利益となります。
(動的計画法、DP)
動的プログラミングを実装するために再帰的または再帰的書き込みが使用されますが、ここでは再帰的書き込みを記憶検索とも呼びます。
理解の開始
フィボナッチ数列:再帰
function F(n){
if(n= 0||n== 1) return 1;
else return F(n-1)+F(n-2);
}
dp[n]=-1 は、F(n) がまだ計算されていないことを意味します
function F(n) {
if(n == 0||n==1) return 1;//递归边界
if(dp[n] != -1) return dp[n]; //已经计算过，直接返回结果，不再重复计算else {
else dp[n] = F(n-1) + F(n-2); //计算F(n)，并保存至dp[n]
return dp [n];//返回F(n)的结果
}
ナンバータワー: 再帰
i 番目の層には i 個の番号があります。ここで、最初のレベルからn 番目のレベルに移動する必要があります。パス上のすべての数値を合計した後に得られる最大合計はいくらですか?
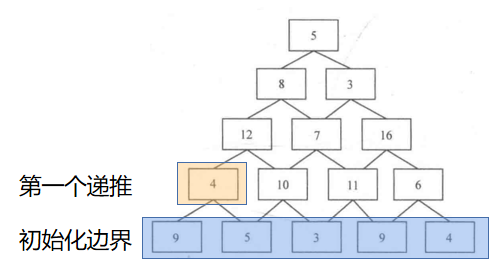
dp[i][j]は、i行目のj番目から最下層までのすべてのパスの和の最大値を表します。
dp[i][i]=max(dp[i-1][j],dp[i-1][j+1])+f[i][j]
漸化式
最小パス合計
mxn 行列 a, 左上隅から開始して、毎回右または下にのみ進むことができ、最終的に右下隅に到達します。パス上のすべての数値の合計がパス合計であり、すべてのパスの合計の最小値になります。パスが出力されます。
dp[i][j] は i から j までの最短パスを表します
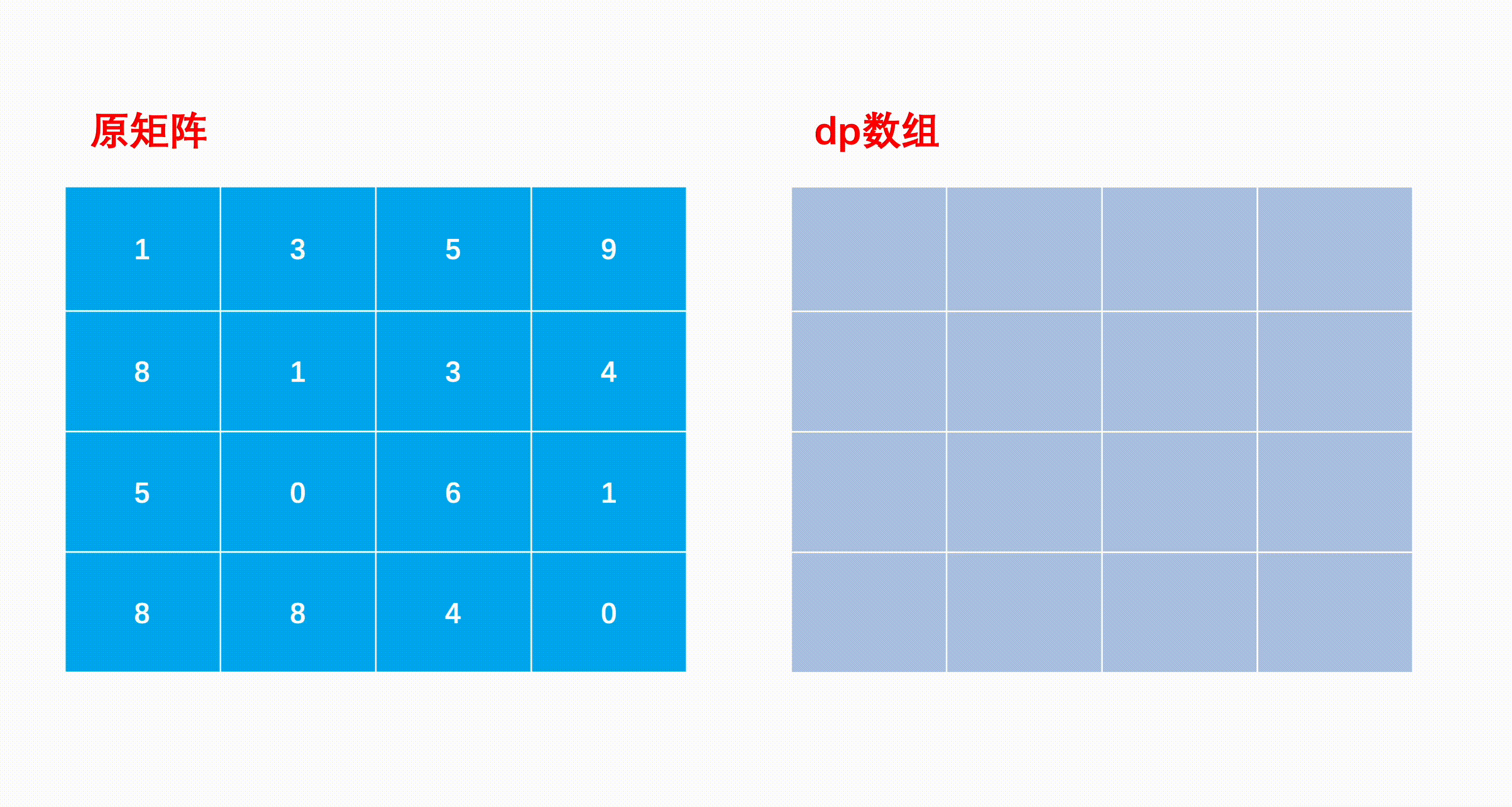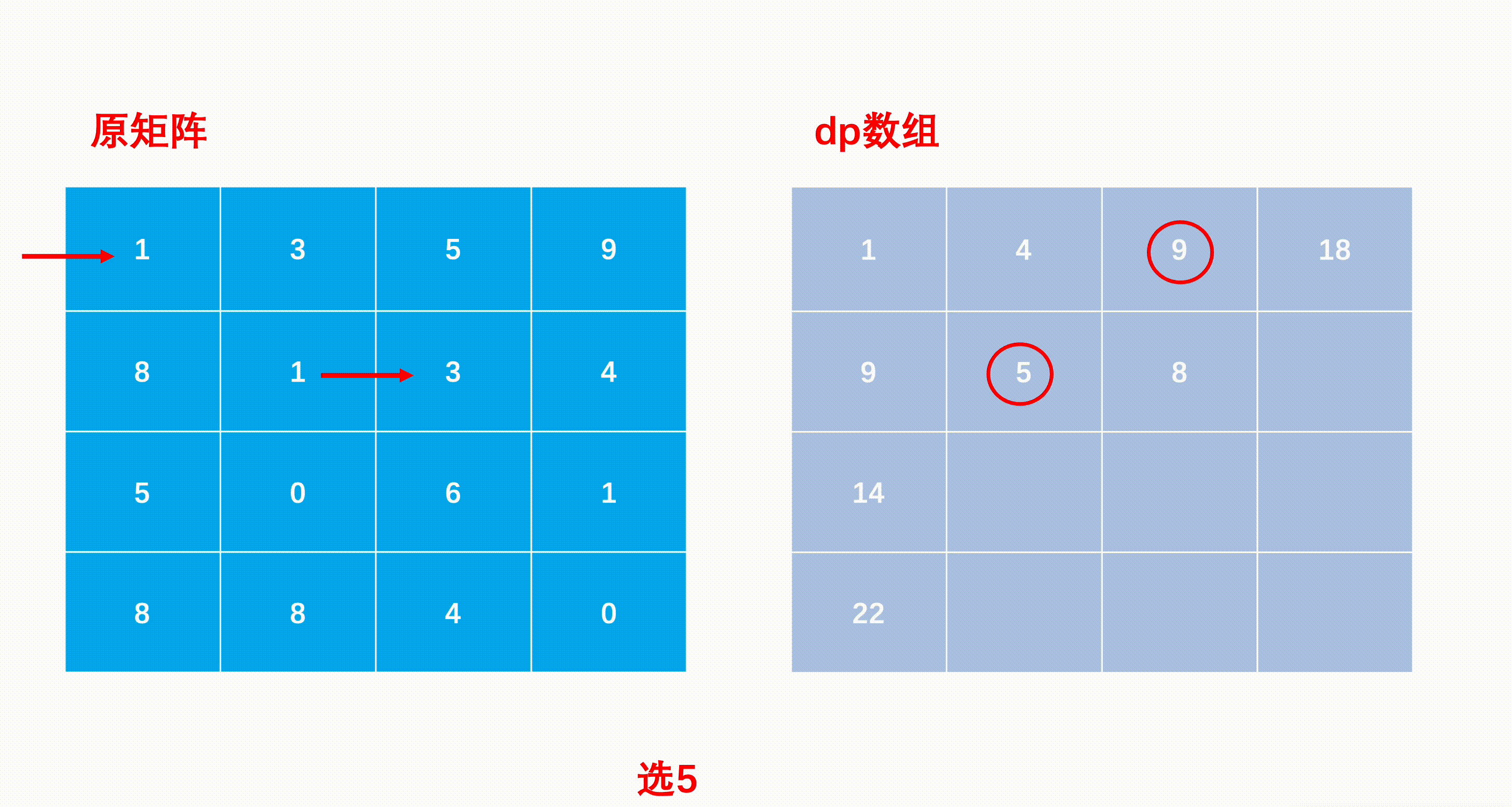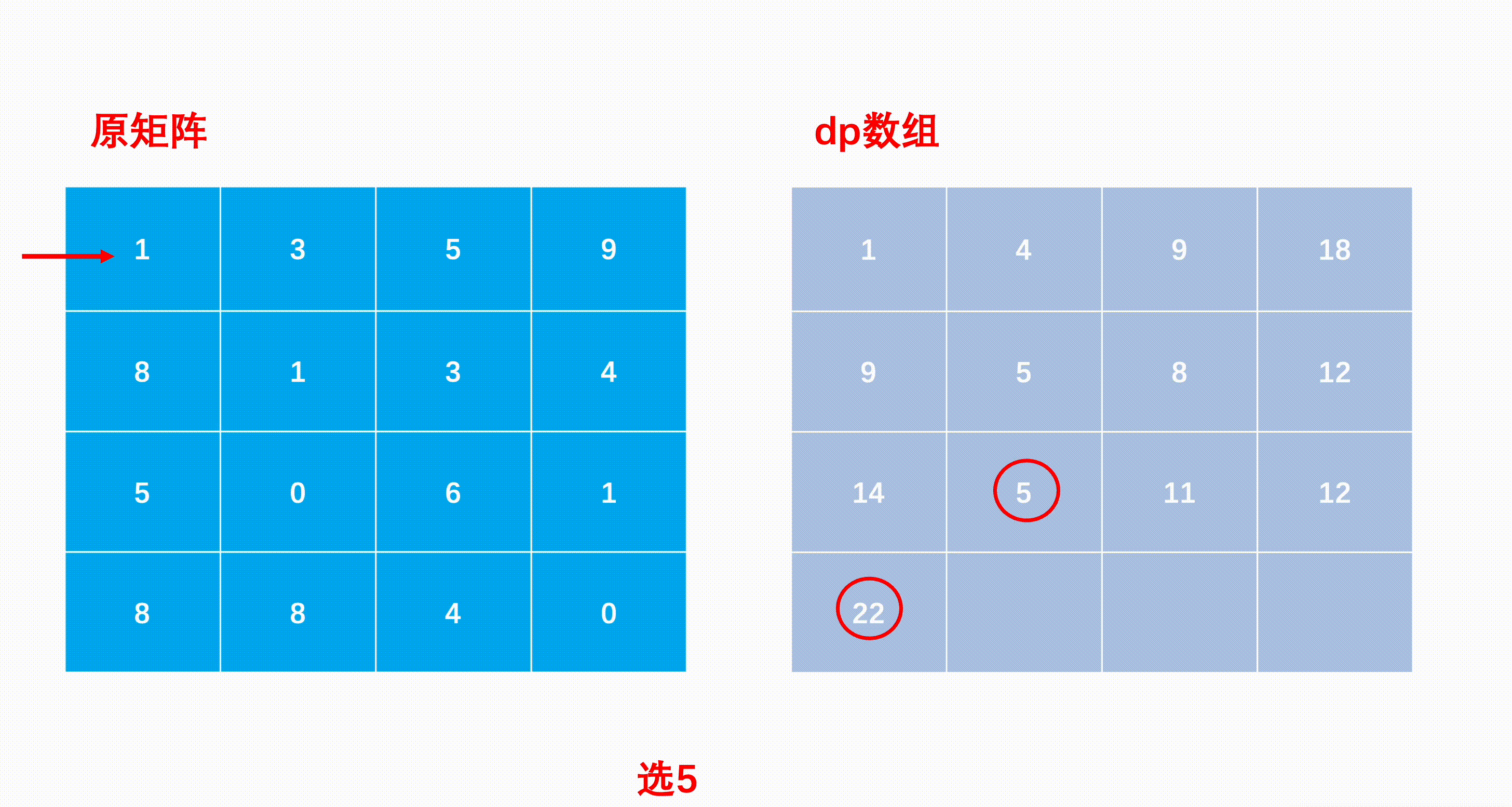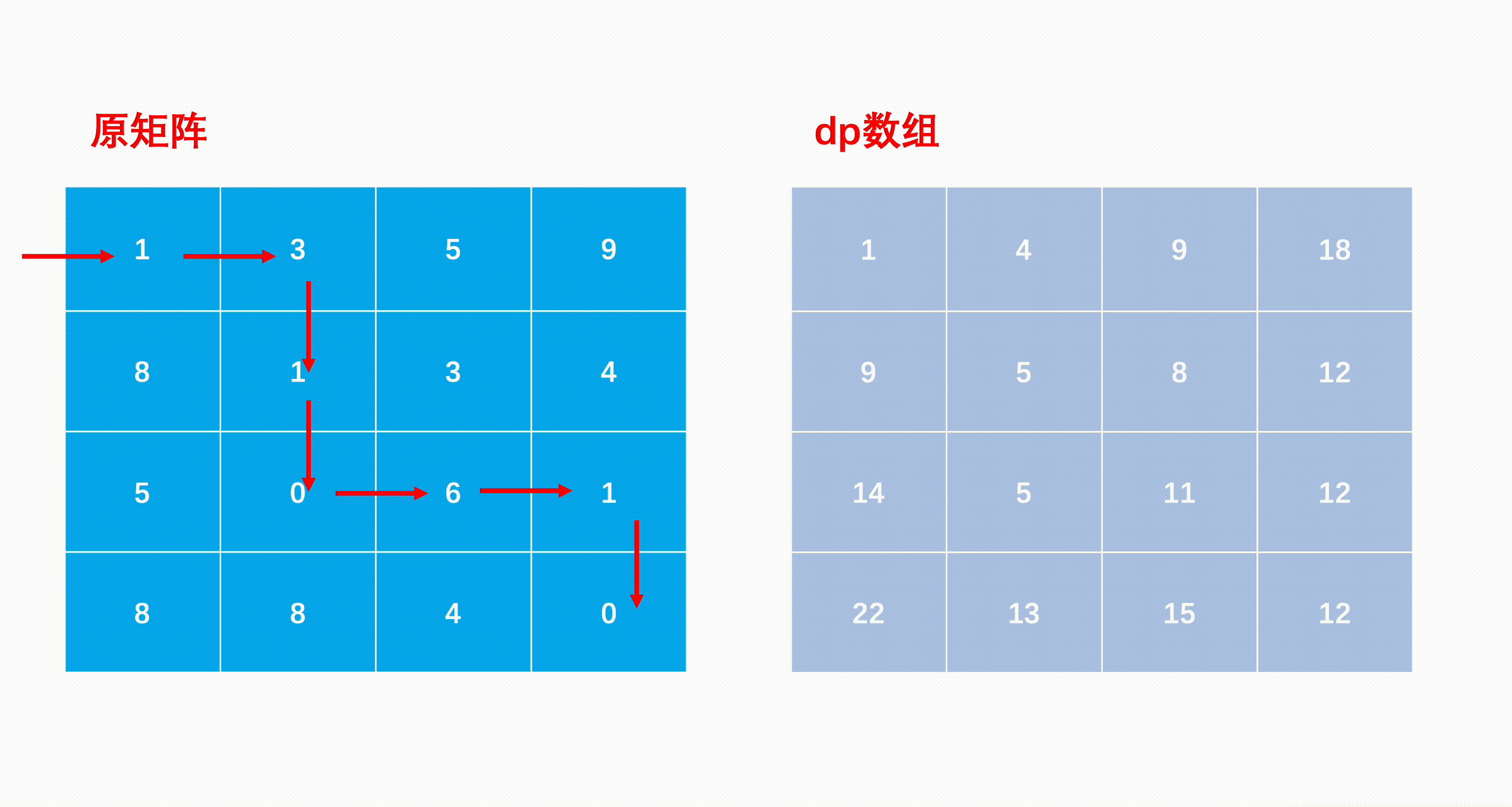
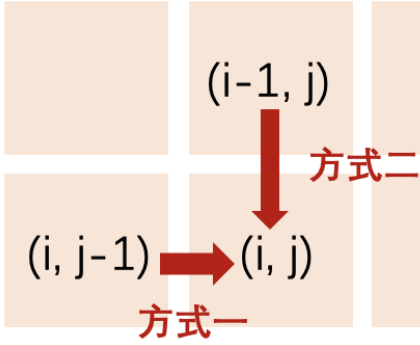
部分問題を解くときの状態遷移方程式：「前の状態」から「次の状態」への再帰式。
dp[i, j] = min(dp[i - 1][j], dp[i][j - 1]) + 行列[i][j]
JavaScript には 2 次元配列の概念はありませんが、配列要素の値を配列と等しくなるように設定できます。
鍵：
- dp[0][i] = dp[0][i - 1] + 行列[0][i];
- dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 行列[i][j];
function minPathSum(matrix) {
var row = matrix.length,
col = matrix[0].length;
var dp = new Array(row).fill(null).map(() => new Array(col).fill(0));
dp[0][0] = matrix[0][0]; // 初始化左上角元素
// 初始化第一行
for (var i = 1; i < col; i++) dp[0][i] = dp[0][i - 1] + matrix[0][i];
// 初始化第一列
for (var j = 1; j < row; j++) dp[j][0] = dp[j - 1][0] + matrix[j][0];
// 动态规划
for (var i = 1; i < row; i++) {
for (var j = 1; j < col; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];
}
}
return dp[row - 1][col - 1]; // 右下角元素结果即为答案
}走査順序
整数分割: 合計に分割し、積を最大化します
実際、2 つの方法で j を 1 からたどって dp[i] を取得できます。
2 つの数値に分割: j * (i - j) を直接乗算します。
3 つ以上の数値に分割します: j * dp[i - j]。これは (i - j) を分割するのと同じです。
dp[i] は dp[i - j] の状態に依存するため、i を前から後ろに走査する必要があります。最初に dp[i - j] があり、次に dp[i] があります。
var integerBreak = function(n) {
let dp = new Array(n + 1).fill(0)
dp[2] = 1
for(let i = 3; i <= n; i++) {
for(let j = 1; j <= i / 2; j++) {
dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
}
}
return dp[n]
};バックパック:: + -> 梱包
フレーム
for 状态1 in 状态1的所有取值：
for 状态2 in 状态2的所有取值：
for ...
dp[状态1][状态2][...] = 择优(选择1，选择2...)
int dp[N+1][W+1]
dp[0][..] = 0
dp[..][0] = 0
for i in [1..N]:
for w in [1..W]:
dp[i][w] = max(
把物品 i 装进背包,
不把物品 i 装进背包
)
return dp[N][W]
...加上边界条件，装不下的时候，只能选择不装01 バックパック：選択不可
重み w[i]、値 c[j]、容量 V を持つ項目が n 個あります。各項目の項目は 1 つだけです。
dp[i][v] は、最初の i 個のアイテム(1≤i≤n, 0≤v≤V) を容量 v のバックパックに積み込むことで得られる最大値を表します。
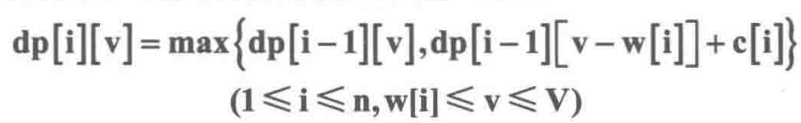
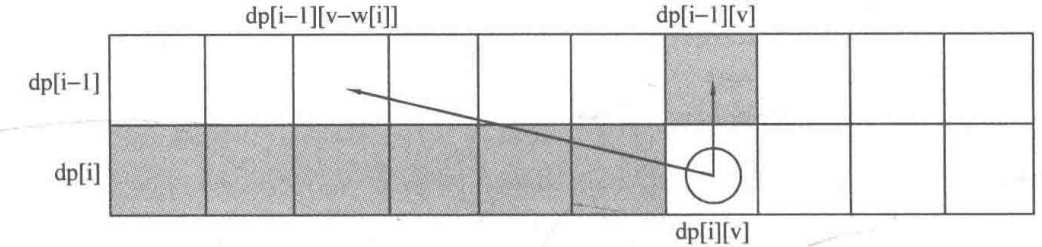
function testWeightBagProblem (weight, value, size) {
// 定义 dp 数组
const len = weight.length,
dp = Array(len).fill().map(() => Array(size + 1).fill(0));
// 初始化
for(let j = weight[0]; j <= size; j++) {
dp[0][j] = value[0];
}
// weight 数组的长度len 就是物品个数
for(let i = 1; i < len; i++) { // 遍历物品
for(let j = 0; j <= size; j++) { // 遍历背包容量
if(j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
console.table(dp)
return dp[len - 1][size];
}
function test () {
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}
test();逆の順序でトラバースします
i を選択: 前のレイヤーの値が上書きされないように、右下隅は左上隅に依存します。
i は選択しないでください: dp[i][v]=dp[i-1][v] 同じ列は影響を受けません
これは基本的に 2 次元配列の走査であり、右下隅の値は前のレイヤーの左上隅の値に依存するため、左側の値がまだレイヤーからのものであることを確認する必要があります。前のレイヤーを右から左に覆います。
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}2 つに分けると、weight[i]==value[i]
1 次元 dp 配列を使用する場合、項目 (値)を走査する for ループは外側の層に配置され、バックパック (重み)を走査する for ループは内側の層に配置され、内側の for ループは逆の順序で横断しました！スクロール配列
最小：dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i])
等和サブセットの分割: 正の整数
- バックパックの体積は和/2です
- バックパックに入れる商品（コレクションの要素）の重さが要素の価値となり、その価値も要素の価値となります。
- バックパックがちょうどいっぱいの場合、合計 / 2 のサブセットが見つかったことを意味します。
- バックパック内の各要素を繰り返し配置することはできません。
var canPartition = function(nums) {
const sum = (nums.reduce((p, v) => p + v));
//奇数
if (sum & 1) return false;
const dp = Array(sum / 2 + 1).fill(0);
for(let i = 0; i < nums.length; i++) {
for(let j = sum / 2; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
if (dp[j] === sum / 2) {
return true;
}
}
}
return dp[sum / 2] === sum / 2;
};最後の石の重さⅡ
/**
* @param {number[]} stones
* @return {number}
*/
var lastStoneWeightII = function (stones) {
let sum = stones.reduce((s, n) => s + n);
let dpLen = Math.floor(sum / 2);
let dp = new Array(dpLen + 1).fill(0);
for (let i = 0; i < stones.length; ++i) {
for (let j = dpLen; j >= stones[i]; --j) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[dpLen] - dp[dpLen];
};組み合わせの数: dp[j] += dp[j - nums[i]];
目標合計: 負でない整数、+ / -
左の組み合わせ - 右の組み合わせ = ターゲット。
左 + 右 = 合計、合計は固定です。右 = 合計 - 左
ここで、式、 left - (sum - left) = target 推定 left = (target + sum)/2 になります。
目標が定まり、和が定まり、左が見つかる。
このときの問題は、集合数に和が残る組み合わせを見つけることです。
dp[j] の意味: j (j を含む) と同じ大きさの体積を袋に入れるには dp[j] 通りの方法があります
nums[i] が得られる限り、dp[j] を作成するには dp[j - nums[i]] 通りの方法があります。
例: dp[j]、j は 5、
- すでに 1 (nums[i]) がある場合、容量 5 のバックパックを作成するには dp[4] の方法があります。
- すでに 2(nums[i]) を持っている場合は、容量 5 のバックパックを作成する dp[3] の方法があります。
- すでに 3 (nums[i]) を持っている場合は、dp[2] に容量 5 のバックパックを作成するメソッドがあります。
- すでに 4 (nums[i]) を持っている場合は、dp[1] に容量 5 のバックパックを作成するメソッドがあります。
- すでに 5 (nums[i]) を持っている場合は、dp[0] に容量 5 のバックパックを作成するメソッドがあります。
それでは、dp[5] を切り上げる、つまりすべての dp[j - nums[i]] を合計する方法は何通りあるでしょうか。
したがって、組み合わせ問題を解くための公式は次のようになります。
dp[j] += dp[j - nums[i]]const findTargetSumWays = (nums, target) => {
const sum = nums.reduce((a, b) => a+b);
if(Math.abs(target) > sum) {
return 0;
}
if((target + sum) % 2) {
return 0;
}
const halfSum = (target + sum) / 2;
let dp = new Array(halfSum+1).fill(0);
dp[0] = 1;
for(let i = 0; i < nums.length; i++) {
for(let j = halfSum; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[halfSum];
};バックパック一式
01のバックパック問題との違いは、各アイテムのピースが無数に存在することです。
順次走査
i を選択: 右側は左側に依存します。同じレイヤーの値が使用されます。左側を最初に生成する必要があります。
i は選択しないでください: dp[i][v]=...dp[i-1][v] 同じ列は影響を受けません
// 先遍历物品，再遍历背包容量
function test_completePack1() {
let weight = [1, 3, 5]
let value = [15, 20, 30]
let bagWeight = 4
let dp = new Array(bagWeight + 1).fill(0)
for(let i = 0; i <= weight.length; i++) {
for(let j = weight[i]; j <= bagWeight; j++) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
}
}
console.log(dp)
}
// 先遍历背包容量，再遍历物品
function test_completePack2() {
let weight = [1, 3, 5]
let value = [15, 20, 30]
let bagWeight = 4
let dp = new Array(bagWeight + 1).fill(0)
for(let j = 0; j <= bagWeight; j++) {
for(let i = 0; i < weight.length; i++) {
if (j >= weight[i]) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
}
}
}
console.log(2, dp);
}バックパック全体の 2 つの for ループの順序は許容されます。
オプションの数: dp[i] += dp[i - nums[j]]
組み合わせ数：外側アイテム、内側バックパック
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
dp[j] += dp[j - coins[i]];
}
}コイン[0] = 1、コイン[1] = 5と仮定します。
まず計算に 1 を加え、次に計算に 5 を加えます。得られるメソッドの数は {1, 5} だけです。そして、{5, 1} の状況は発生しません
配置数：アウターリュック、インナーアイテム
for (int j = 0; j <= amount; j++) { // 遍历背包容量
for (int i = 0; i < coins.size(); i++) { // 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}バックパックの容量の各値は、{1, 5} と {5, 1} を含め、1 と 5 から計算されます。
dp[j]は外層にあり、1が見つかったら5を更新、5が見つかったら1を更新します。
チェンジエクスチェンジⅡ：組み合わせ数
さまざまな額面のコインと合計金額が与えられます。合計金額を構成するコインの組み合わせの数を計算する関数を作成します。各金種のコインが無限にあると仮定します。
例 1:
- 入力: 金額 = 5、コイン = [1、2、5]
- 出力: 4
説明: 合計金額を切り上げるには 4 つの方法があります。
- 5=5
- 5=2+2+1
- 5=2+1+1+1
- 5=1+1+1+1+1
const change = (amount, coins) => {
let dp = Array(amount + 1).fill(0);
dp[0] = 1;
for(let i =0; i < coins.length; i++) {
for(let j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}組み合わせ和IV：順列数
const combinationSum4 = (nums, target) => {
let dp = Array(target + 1).fill(0);
dp[0] = 1;
for(let i = 0; i <= target; i++) {
for(let j = 0; j < nums.length; j++) {
if (i >= nums[j]) {
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
};最小数
両替
純粋な完全なナップザックは、完全なナップザックの最大値を決定します。合計を構成する要素が順序どおりであるかどうかは問題ではありません。つまり、順序が正しいかどうかは問題ではありません。
// 遍历物品
const coinChange = (coins, amount) => {
if(!amount) {
return 0;
}
let dp = Array(amount + 1).fill(Infinity);
dp[0] = 0;
for(let i = 0; i < coins.length; i++) {
for(let j = coins[i]; j <= amount; j++) {
dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);
}
}
return dp[amount] === Infinity ? -1 : dp[amount];
}完全平方数
完全平方数はアイテム（無制限に使用可能）、正の整数 n はバックパックです。このバックパックを完成させるには、少なくとも何個のアイテムが必要ですか?
for (int j = 1; j * j <= i; j++) { // 遍历物品
dp[i] = min(dp[i - j * j] + 1, dp[i]);
}判断
単語の分割
単語はアイテムであり、文字列 s はバックパックです。単語が文字列 s を形成できるかどうかは、アイテムがバックパックを満たすことができるかどうかを問うことと同じです。
分割すると、辞書内の単語を再利用できるため、完全なバックパックが完成します。
dp[i]: 文字列の長さが i の場合、dp[i] は true です。これは、辞書に表示される 1 つ以上の単語に分割できることを意味します。
dp[j] が true であると判断され、区間 [j, i] の部分文字列が辞書に表示される場合、dp[i] は true でなければなりません。(j < i )。
したがって、再帰式は if([j, i] この区間の部分文字列が辞書に表示されます && dp[j] が true) then dp[i] = true となります。
const wordBreak = (s, wordDict) => {
let dp = Array(s.length + 1).fill(false);
dp[0] = true;
for(let i = 0; i <= s.length; i++){
for(let j = 0; j < wordDict.length; j++) {
if(i >= wordDict[j].length) {
if(s.slice(i - wordDict[j].length, i) === wordDict[j] && dp[i - wordDict[j].length]) {
dp[i] = true
}
}
}
}
return dp[s.length];
}サブセット: dp[i] は最大でもオプションです
お買い得
1と0
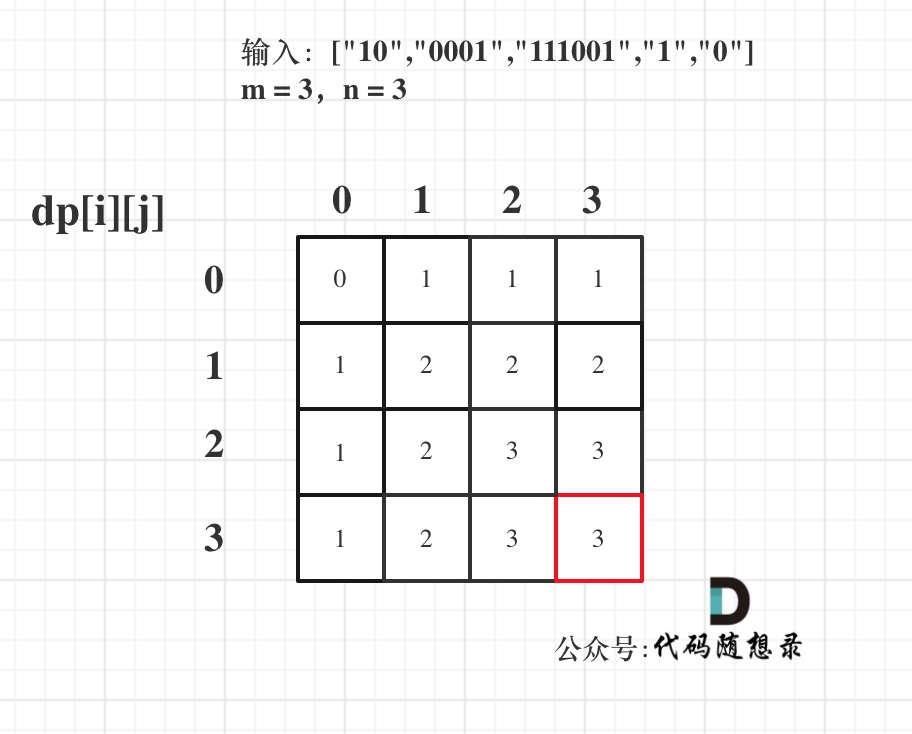
最大 m 個の 0 と n 個の 1 を持つ strs の最大のサブセットのサイズを見つけて返します。
-
入力：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
-
出力: 4
-
説明: 最大 5 つの 0 と 3 つの 1 を持つ最大のサブセットは {"10","0001","1","0"} であるため、答えは 4 です。質問を満たす他の小さなサブセットには、{"0001","1"} および {"10","1","0"} があります。{"111001"} には 4 つの 1 が含まれており、n の値より大きいため、質問の意味を満たしていません。
dp[i][j]: 最大 i 個の 0 と j 個の 1 を持つ strs の最大のサブセットのサイズは dp[i][j] です。
漸化式を決定する
dp[i][j] は、前の strs 内の文字列から推定できます。strs 内の文字列には、zeroNum 個の 0 と oneNum 1 があります。
dp[i][j] は dp[i - zeroNum][j - oneNum] + 1 になります。
次に、走査プロセス中に dp[i][j] の最大値を取得します。
したがって、再帰式は次のようになります。 dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
この時点で、01 バックパックの漸化式を思い出してください。 dp[j] = max(dp[j], dp[j -weight[i]] + value[i]);
比較してみると、文字列のzeroNumとoneNumが商品の重さ(weight[i])に相当することがわかります。
const findMaxForm = (strs, m, n) => {
const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));
let numOfZeros, numOfOnes;
for(let str of strs) {
numOfZeros = 0;
numOfOnes = 0;
for(let c of str) {
if (c === '0') {
numOfZeros++;
} else {
numOfOnes++;
}
}
for(let i = m; i >= numOfZeros; i--) {
for(let j = n; j >= numOfOnes; j--) {
dp[i][j] = Math.max(dp[i][j], dp[i - numOfZeros][j - numOfOnes] + 1);
}
}
}
return dp[m][n];
};2 つに分割します:weight[i]==value[i]
サブシーケンス: dp[i] は添え字 i - 1/i で終わります (相対的な順序を維持します)
for(let i = 1; i < nums.length; i++)
for(let j = 0; j < i; j++)
継続的な
最長の回文部分文字列
dp[i][j]は、S[i]～S[j]で表される部分文字列が回文部分文字列であるかどうかを示し、回文部分文字列である場合は1、そうでない場合は0です。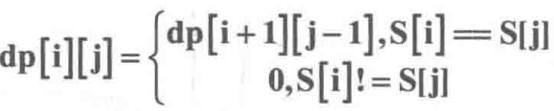
最大部分列合計
dp[i]: 添え字 i (nums[i] で終わる) を含む最大連続部分列合計は dp[i] です。
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
最長反復部分配列
dp[i][j]: A は添字 i - 1 で終わり、B は添字 j - 1 で終わります。最も長く繰り返される部分配列の長さは dp[i][j] です。
A[i - 1] と B[j - 1] が等しい場合、dp[i][j] = dp[i - 1][j - 1] + 1 となります。
動的プログラミング
const findLength = (A, B) => {
// A、B数组的长度
const [m, n] = [A.length, B.length];
// dp数组初始化，都初始化为0
const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
// 初始化最大长度为0
let res = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 遇到A[i - 1] === B[j - 1]，则更新dp数组
if (A[i - 1] === B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
// 更新res
res = dp[i][j] > res ? dp[i][j] : res;
}
}
// 遍历完成，返回res
return res;
};
スクロール配列
const findLength = (nums1, nums2) => {
let len1 = nums1.length, len2 = nums2.length;
// dp[i][j]: 以nums1[i-1]、nums2[j-1]为结尾的最长公共子数组的长度
let dp = new Array(len2+1).fill(0);
let res = 0;
for (let i = 1; i <= len1; i++) {
for (let j = len2; j > 0; j--) {
if (nums1[i-1] === nums2[j-1]) {
dp[j] = dp[j-1] + 1;
} else {
dp[j] = 0;
}
res = Math.max(res, dp[j]);
}
}
return res;
}不連続な
最長共通部分列(LCS)
最長共通部分列: 部分列は不連続な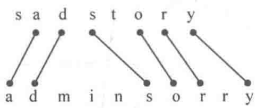
「sadstory」と「adminsorry」にすることができます。最長の共通部分列は「adsory」です。
dp[i][j]: strA[i] と strB[j]の前のLCS 長さ、添字は 1 から始まります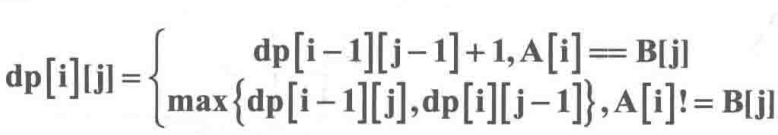
互いに素な線: 最長の共通部分列の長さ
直線は交差できません。つまり、文字列 A には文字列 B と同一の部分列があり、この部分列は相対順序を変更できません。相対順序が変わらない限り、同じ数値を結ぶ直線は交差しません。
異なるサブシーケンス
dp[i][j]: i-1 で終わる s 部分列に出現する j-1 で終わる t の数は dp[i][j] です
const numDistinct = (s, t) => {
let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));
for(let i = 0; i <=s.length; i++) {
dp[i][0] = 1;
}
for(let i = 1; i <= s.length; i++) {
for(let j = 1; j<= t.length; j++) {
if(s[i-1] === t[j-1]) {
//不用s[i - 1]来匹配，个数为dp[i - 1][j]
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
} else {
dp[i][j] = dp[i-1][j]
}
}
}
return dp[s.length][t.length];
};最長の昇順サブシーケンス
dp[i] は、i より前の i を含む、nums[i] で終わる最長の増加サブシーケンスの長さを表します。
位置 i の最長の昇順サブシーケンスは、0 から i-1 までの j の各位置の最長の昇順サブシーケンスの最大値 + 1 に等しくなります。
所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
const lengthOfLIS = (nums) => {
let dp = Array(nums.length).fill(1);
let result = 1;
for(let i = 1; i < nums.length; i++) {
for(let j = 0; j < i; j++) {
if(nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
result = Math.max(result, dp[i]);
}
return result;
};最長の回文部分列
const longestPalindromeSubseq = (s) => {
const strLen = s.length;
let dp = Array.from(Array(strLen), () => Array(strLen).fill(0));
for(let i = 0; i < strLen; i++) {
dp[i][i] = 1;
}
for(let i = strLen - 1; i >= 0; i--) {
for(let j = i + 1; j < strLen; j++) {
if(s[i] === s[j]) {
dp[i][j] = dp[i+1][j-1] + 2;
} else {
dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
}
}
}
return dp[0][strLen - 1];
};強盗: サブセット + 最良の値 + 連続して盗むことはできません
配列
dp[i]: 添え字 i 内の家 (i を含む) を考慮すると、盗まれる最大量は dp[i] です。
dp[i] を決定する要素は、i 番目の部屋を盗むかどうかです。
i 番目の部屋が盗まれた場合、dp[i] = dp[i - 2] + nums[i]、つまり、i-1 番目の部屋は考慮されてはならず、添字 i-2 (i- を含む) を見つけます。 2) 屋内の家については、盗まれる最大金額は dp[i-2] に i 番目の部屋から盗まれたお金を加えたものです。
i 番目の部屋を盗まない場合は、dp[i] = dp[i - 1]、つまり i-1 番目の部屋を考慮します (ここでは考慮されており、必ずしも盗むことを意味するわけではないことに注意してください) i-1 ルームを盗まなければなりません。これは多くの学生に混同されやすいです。ポイント)
次に、dp[i] は最大値をとります。つまり、 dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
指輪
影響を受けるのは最初と最後の要素です
配列の場合、リングが形成されるときは主に 3 つの状況があります。
- ケース 1: 最初と最後の要素 = 線形配列を含まないことを検討します。
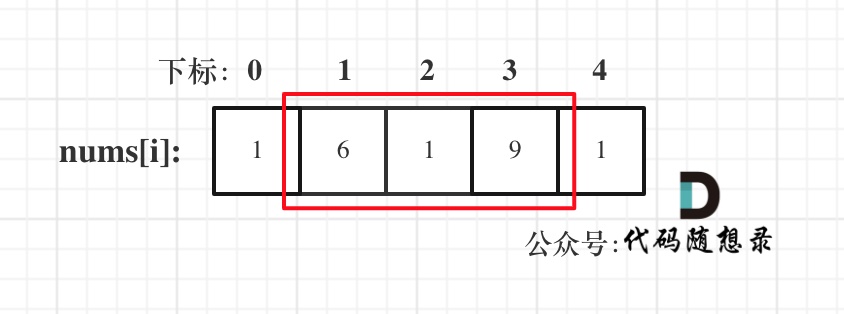
- ケース 2: 最初の要素を含めるが最後の要素は含めないことを検討する
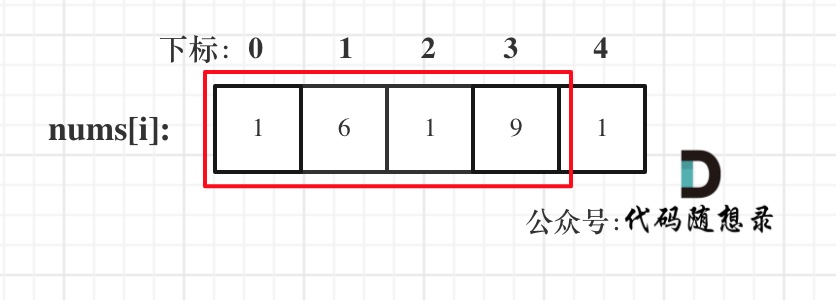
- シナリオ 3: 最初の要素ではなく末尾要素を含めることを検討する
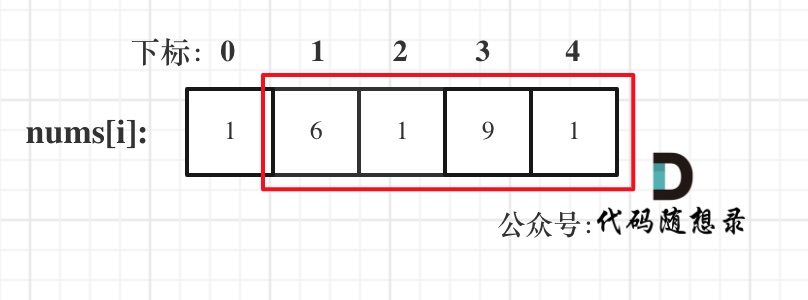
ここで「consider」を使用していることに注意してください。たとえば、ケース 3 では、末尾要素が含まれているとみなされますが、末尾要素を選択する必要はありません。ケース 3 では、nums[1] と nums[3] が最大になります。
状況 2 と状況 3 には両方に状況 1 が含まれるため、状況 2 と状況 3 のみが考慮されます。
var rob = function(nums) {
const n = nums.length
if (n === 0) return 0
if (n === 1) return nums[0]
const result1 = robRange(nums, 0, n - 2)
const result2 = robRange(nums, 1, n - 1)
return Math.max(result1, result2)
};
const robRange = (nums, start, end) => {
if (end === start) return nums[start]
const dp = Array(nums.length).fill(0)
dp[start] = nums[start]
dp[start + 1] = Math.max(nums[start], nums[start + 1])
for (let i = start + 2; i <= end; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])
}
return dp[end]
}二分木
添字０はノードを盗まない場合に得られる最大金額を記録し、添字１はノードを盗む場合に得られる最大金額を記録する。
したがって、この質問の dp 配列は長さ 2 の配列です。
次に、長さ 2 の配列がツリー内の各ノードのステータスをどのようにマークできるのか疑問に思う学生もいるかもしれません。
再帰プロセス中に、システム スタックが再帰の各レベルのパラメータを保存することを忘れないでください。
ポストオーダートラバーサル: 再帰関数の戻り値を使用して次の計算を実行します。
const rob = root => {
// 后序遍历函数
const postOrder = node => {
// 递归出口
if (!node) return [0, 0];
// 遍历左子树
const left = postOrder(node.left);
// 遍历右子树
const right = postOrder(node.right);
// 不偷当前节点，左右子节点都可以偷或不偷，取最大值
const DoNot = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
// 偷当前节点，左右子节点只能不偷
const Do = node.val + left[0] + right[0];
// [不偷，偷]
return [DoNot, Do];
};
const res = postOrder(root);
// 返回最大值
return Math.max(...res);
};株の売買
売買は一度だけ
まず、現金は 0 に設定されます。株を買うとお金がかかり (負の数になります)、株を売るとお金が生まれます。
毎日、株には 2 つの状態があります: 保有している場合と保有していない場合です。
再帰式 dp[i] の場合[0 ] = max(dp[i - 1][0], -price[i])、
実際には、i 日に株を買うかどうかを意味します。買えば、お金は減ります。買わないでください。前日の状態が維持されます。買うか買わないかの 2 つの状況のうち、残高が多い方を選択します。for
dp[i][1] = max(dp[i - 1] ][1], dp[i - 1][0] + 価格[i])
i 日に株を売るかどうかを意味します。売れば儲けます。売らなければ、前日の状態を維持します。売った場合と売らなかった場合とで、残っているお金が最も多い方が優先されます。株を売りたい場合は、以前に株を購入している必要があります。つまり、dp[i - 1] となります。 [0] + 価格[i]
欲張り：左の最小値と右の最大値をとり、その差が最大利益となります。
int maxProfit(vector<int>& prices) {
int low = INT_MAX;
int result = 0;
for (int i = 0; i < prices.size(); i++) {
low = min(low, prices[i]); // 取最左最小价格
result = max(result, prices[i] - low); // 直接取最大区间利润
}
return result;
}再度購入する前に売却する
const maxProfit = (prices) => {
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
// dp[i][0] 表示第i天持有股票所得现金。
// dp[i][1] 表示第i天不持有股票所得最多现金
dp[0][0] = 0 - prices[0];
dp[0][1] = 0;
for (let i = 1; i < prices.length; i++) {
// 如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来
// 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
// 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
// 在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来
// 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
// 第i天卖出股票，所得现金就是按照今天股票佳价格卖出后所得现金即：prices[i] + dp[i - 1][0]
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
}
return dp[prices.length - 1][1];
};貪欲:利益は日次で分割されます
0 日目に買って 3 日目に売る場合、利益は価格[3] - 価格[0] となります。
(価格[3] - 価格[2]) + (価格[2] - 価格[1]) + (価格[1] - 価格[0])に相当します。
このとき、利益は 0 日目から 3 日目までの全体として考えるのではなく、日単位のディメンションに分解されます。
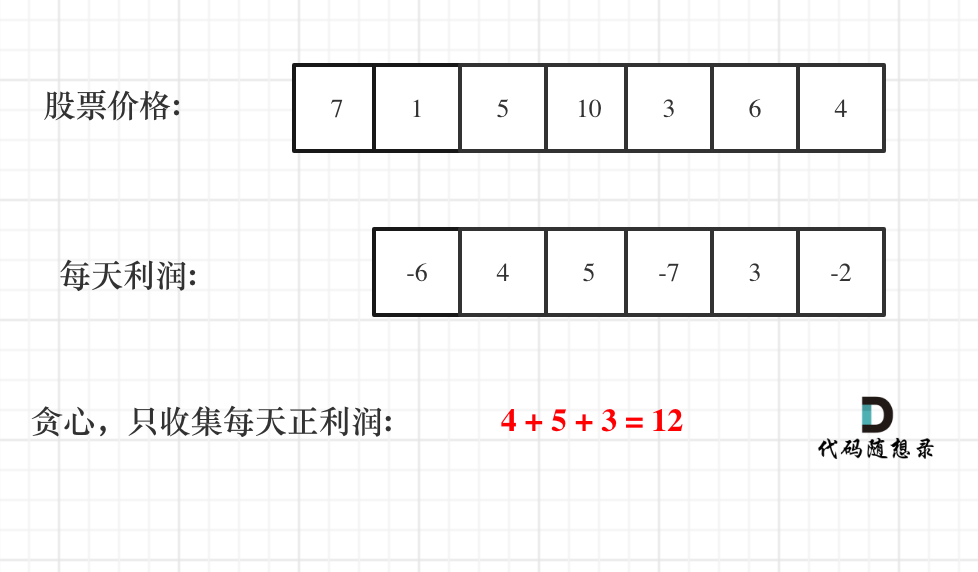
var maxProfit = function(prices) {
let result = 0
for(let i = 1; i < prices.length; i++) {
result += Math.max(prices[i] - prices[i - 1], 0)
}
return result
};最大2回の取引
- dp 配列と添字の意味を確認する
1日に合計5つの州があり、
- 操作なし (実際には、このステータスを設定する必要はありません)
- 初めて株を保有する
- 初めて株を保有しない
- 2度目の株保有
- 2度目の株式保有はしない
dp[i][j] の i は i 日目を表し、j は 5 つの状態 [0 ～ 4] で、dp[i][j] は i 日目に状態 j に残っている最大現金を表します。
- 漸化式を決定する
dp[i][1] 状態に到達するには、次の 2 つの特定の操作があります。
- 操作 1: i 日目に株を買う場合、dp[i][1] = dp[i-1][0] - 価格[i]
- 操作 2: i 日目には操作はありませんが、前日の購入ステータスが使用されます。つまり、 dp[i][1] = dp[i - 1][1]
それでは、dp[i][1] は dp[i-1][0] - 価格 [i] または dp[i - 1][1] を選択する必要がありますか?
最大のものを選択する必要があるため、 dp[i][1] = max(dp[i-1][0] - 価格[i], dp[i - 1][1]);
同様に、 dp[i][2] にも 2 つの演算があります。
- 操作 1: 株式が i 日目に売却された場合、dp[i][2] = dp[i - 1][1] + 価格[i]
- 操作 2: i 日目には操作はなく、前日の株式売却のステータスが使用されます。つまり、 dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + 価格[i], dp[i - 1][2])
同様に、残りのステータス部分を導出できます。
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - 価格[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + 価格[i]);
- dp配列を初期化する方法
0 日目には操作はありません。最も簡単に考えるのは 0、つまり dp[0][0] = 0; です。
0 日目に最初の購入操作を実行します。 dp[0][1] = -prices[0];
0日目に最初の売り操作を行う場合、初期値はいくらにすればよいですか?
まだ買っていない場合、どうやって売ることができますか？実際、同じ日に買って同じ日に売ることは誰でも理解できるので、 dp[0][2] = 0;
0 日目の 2 回目の購入操作では、初期値はいくらにすべきでしょうか? 初めて購入したことがない場合、2 回目の購入をどのように初期化すればよいのかと疑問に思う学生も多いかもしれません。
2回目の購入は、最初の販売の状況によって異なります。実際には、0日目に初めて購入し、初めて販売し、その後再度購入（2回目の購入）するのと同じです。現金を手元に持っていれば、買い物をすればそれに応じて現金が減っていきます。
したがって、2 番目の購入操作は次のように初期化されます。 dp[0][3] = -prices[0];
同様に、2 回目の販売では dp[0][4] = 0 を初期化します。
最大 k 個のペン
- 0は何も操作しないことを意味します
- 1回目の購入
- 2 初売り
- 3秒で購入
- 4 セカンドセール
- ……
0 を除いて、偶数が売り、奇数が買いです。
この質問では最大 K 個のトランザクションが存在する必要があり、その場合、j の範囲は 2 * k + 1 として定義されます。
// 方法一：动态规划
const maxProfit = (k,prices) => {
if (prices == null || prices.length < 2 || k == 0) {
return 0;
}
let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0));
for (let j = 1; j < 2 * k; j += 2) {
dp[0][j] = 0 - prices[0];
}
for(let i = 1; i < prices.length; i++) {
for (let j = 0; j < 2 * k; j += 2) {
dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
}
}
return dp[prices.length - 1][2 * k];
};
// 方法二：动态规划+空间优化
var maxProfit = function(k, prices) {
let n = prices.length;
let dp = new Array(2*k+1).fill(0);
// dp 买入状态初始化
for (let i = 1; i <= 2*k; i += 2) {
dp[i] = - prices[0];
}
for (let i = 1; i < n; i++) {
for (let j = 1; j < 2*k+1; j++) {
// j 为奇数：买入状态
if (j % 2) {
dp[j] = Math.max(dp[j], dp[j-1] - prices[i]);
} else {
// j为偶数：卖出状态
dp[j] = Math.max(dp[j], dp[j-1] + prices[i]);
}
}
}
return dp[2*k];
};凍結期間
4 つの州:
- 状態 1: 株式保有状態 (今日株式を購入、または以前に株式を購入し、何も操作せずに保有)
- 在庫状況を保有していない場合、販売在庫状況は 2 つあります。
- 状態2: 株式を売却した状態を維持する(2日前に株式を売却し、1日の凍結期間を経過した、または前日に株式を売却し、何も操作していない)
- ステータス 3: 今すぐ株を売却する
- ステータス 4: 今日は凍結期間状態ですが、凍結期間状態は持続可能ではなく、1 日だけです。
株式購入状態(状態 1)、つまり dp[i][0] に到達すると、次の 2 つの特定の操作があります。
- 操作 1: 株式は前日に保持されていました (状態 1)、dp[i][0] = dp[i - 1][0]
- 操作 2: 今日購入しました。状況は 2 つあります
- 前日は凍結期間 (状態 4)、dp[i - 1][3] - 価格[i]
- 前日は株式を売った状態 (状態 2)、dp[i - 1][1] - 価格[i]
那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - 価格[i], dp[i - 1][1] - 価格[i] );
株式販売状態(状態 2)、つまり dp[i][1] を維持するには、次の 2 つの特定の操作があります。
- 操作 1: 前日は状態 2 でした
- 動作２：前日は凍結期間（状態４）
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
今日株を売却する状態(状態 3)、つまり dp[i][2] に到達するとき、操作は 1 つだけです。
在庫は昨日保有され (状態 1)、今日売却された必要があります
即ち：dp[i][2] = dp[i - 1][0] + 価格[i];
フリーズ期間状態(状態 4)、つまり dp[i][3] に到達すると、操作は 1 つだけになります。
昨日株式を売却しました (ステータス 3)
dp[i][3] = dp[i - 1][2];
上記の分析を要約すると、再帰コードは次のようになります。
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];手数料
// 贪心思路
var maxProfit = function(prices, fee) {
let result = 0
let minPrice = prices[0]
for(let i = 1; i < prices.length; i++) {
if(prices[i] < minPrice) {
minPrice = prices[i]
}
if(prices[i] >= minPrice && prices[i] <= minPrice + fee) {
continue
}
if(prices[i] > minPrice + fee) {
result += prices[i] - minPrice - fee
// 买入和卖出只需要支付一次手续费
minPrice = prices[i] -fee
}
}
return result
};
// 动态规划
/**
* @param {number[]} prices
* @param {number} fee
* @return {number}
*/
var maxProfit = function(prices, fee) {
// 滚动数组
// have表示当天持有股票的最大收益
// notHave表示当天不持有股票的最大收益
// 把手续费算在买入价格中
let n = prices.length,
have = -prices[0]-fee, // 第0天持有股票的最大收益
notHave = 0; // 第0天不持有股票的最大收益
for (let i = 1; i < n; i++) {
// 第i天持有股票的最大收益由两种情况组成
// 1、第i-1天就已经持有股票，第i天什么也没做
// 2、第i-1天不持有股票，第i天刚买入
have = Math.max(have, notHave - prices[i] - fee);
// 第i天不持有股票的最大收益由两种情况组成
// 1、第i-1天就已经不持有股票，第i天什么也没做
// 2、第i-1天持有股票，第i天刚卖出
notHave = Math.max(notHave, have + prices[i]);
}
// 最后手中不持有股票，收益才能最大化
return notHave;
};