記事ディレクトリ
序文

ROS は、rviz や gazebo など、高度に統合された多くの開発ツールを開発者に提供します。rviz は画像、モデル、パスなどの情報を表示できる 3 次元可視化ツールですが、これらのデータはトピックやパラメータの形で公開されていることが前提です。このブロガーは主に rviz の 3D プラットフォームを利用して座標変換とロボットの 3D モデリングを学習しています
1. 空間座標変換の原理
1. ポーズの説明
ポーズの説明を学ぶ前に、まずマトリックスの性質を理解する必要があります。行列を関数に関連付けてマッピングの変更として理解すると、行列の本質は基底ベクトルの空間変換を記述することであり、行列式は基底ベクトルの変換によって囲まれる領域を正確に表現します。
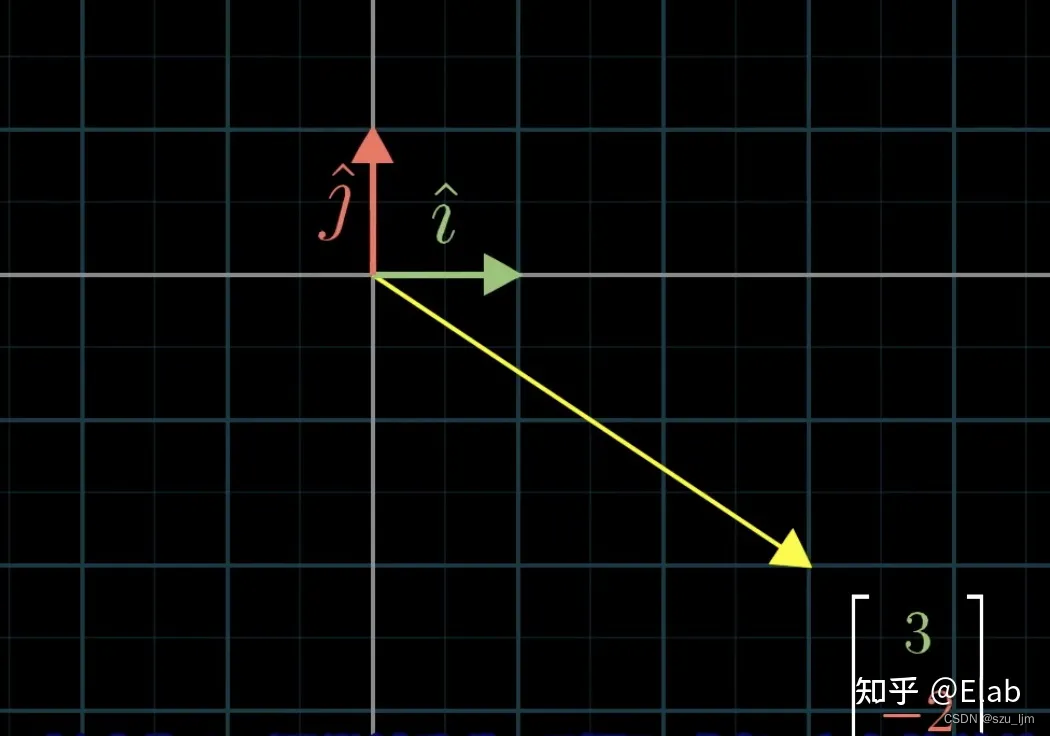
私 \boldsymbol{i}iとj \boldsymbol{j}j は2 次元平面を形成するための最も単純な基底のペアであり、行列はこれら 2 つの基底ベクトルのペアの線形変換、関数 a ⃗ = f ( b ⃗ ) \vec{a} に似た関数に焦点を当てています。
= f(\vec{b})ある=f (b)
比如,[ ij ] \left[ \begin{array}{ccc} i \\ j \end{array} \right ][私j]この基底は [ 3 2 − 2 1 ] \left[ \begin{array}{ccc} 3 & 2\\ -2 & 1 \end{array} \right ] を通過します。[3− 221]マッピング、iii は( 3 , − 2 ) (3,-2)になります( 3 、− 2 )この新しい基底ベクトルjjjは( 2 , 1 ) (2,1)になります。( 2 、1 )この新しい基底ベクトルにより、2 次元平面全体が次のように変わります。
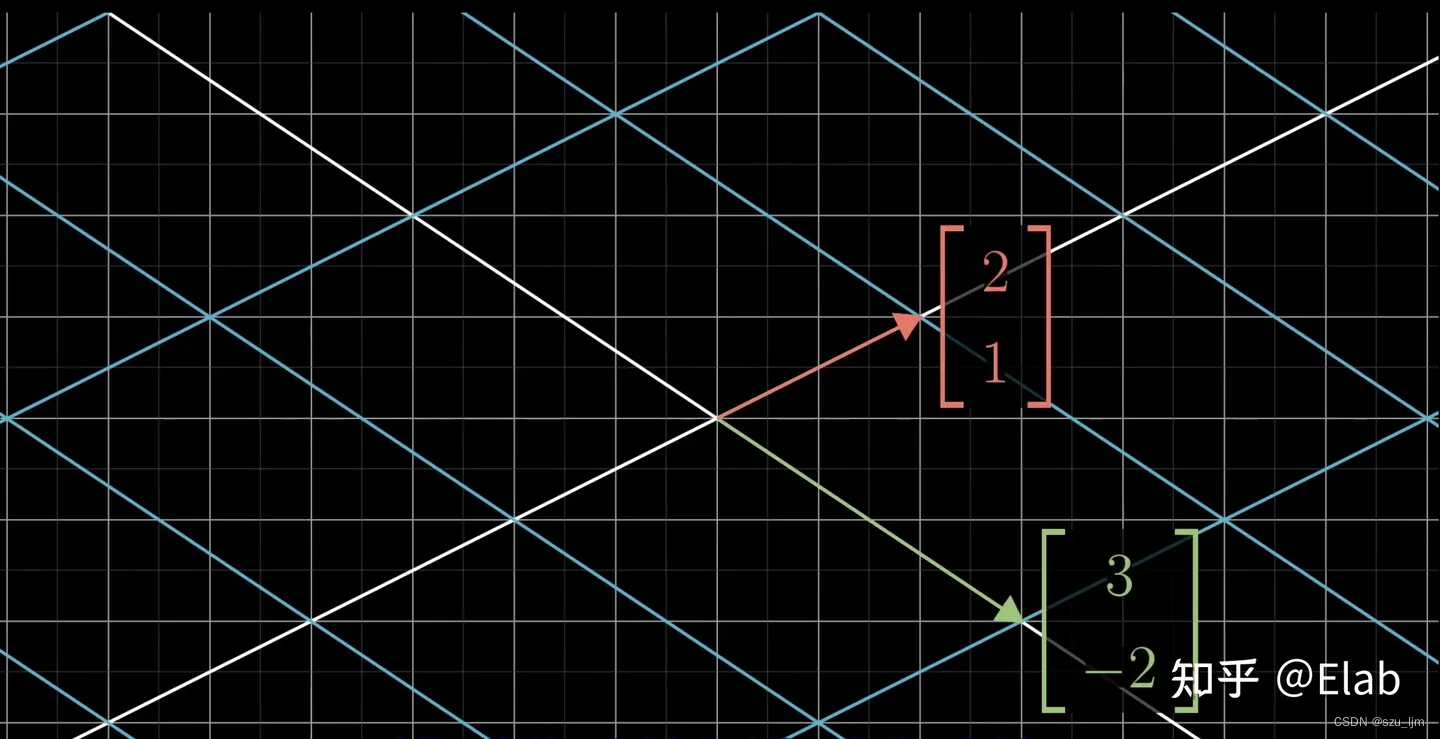
変更された 2 つの基底ベクトルを次のように行列に入れます。したがって、この行列は[ 3 2 − 2 1 ] \left[ \begin{ array} {ccc} 3 & 2\\ -2 & 1 \end{配列} \right ][3− 221] は2 次元空間への変換マッピングを表し、2 つの列は変換されたi \boldsymbol{i}iとj \boldsymbol{j}j。
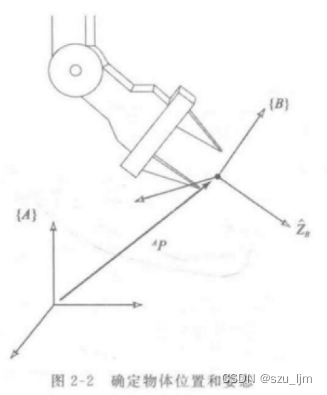
位置と姿勢を表すポーズについて話しましょう。空間座標系OXYZ OXYZ内の任意の剛体OX Y Zでは、位置と姿勢を使用して、その位置ステータスを正確かつ一意に表現できます。デカルト座標系 {A} の場合、空間内の任意の点pppの位置は 3x1 列ベクトルAP ^{A}Pとして使用できます。A P配列
AP = [ pxpypz ] ^{A}P = \left[ \begin{array}{ccc} p_{x}\\ p_{y}\\ p_{z} \end{array} \right ]AP _=
p×pはいpz
主な座標系がA{A}であると仮定します。A ,我们用 X B ˆ 、 Y B ˆ 、 Z B ˆ \^{X_{B}}、\^{Y_{B}}、\^{Z_{B}} バツB^、YB^、ZB^別の座標系B {B}を表すBの 3 つの軸の単位ベクトル、次に座標系B {B}Bは座標系A{A}定義されたバーを持つ境界サイクル= ( AXB ^ AYB ^ AZB ^ ) = [ XB ^ ∙ XA ^ YB ^ ∙ XA ^ ZB ^ ∙ XA ^ XB ^ ∙ YA ^ YB ^ ∙ YA ^ YB ^ ∙ OF ^ XB ^ ∙ ZA ^ YB ^ ∙ ZA ^ ZB ^ ∙ ZA ^ ] _{B}^{A}R = ( ^{A}\^{X_{B}} ^{A}\^{Y_{B}} ^ {A}\^{Z_{B}} ) = \left[\begin{array}{ccc}\^{X_{B}} ∙ \^{X_{A}} & \^{Y_{B} } ∙ \^{X_{A}} & \^{Z_{B}} ∙ \^{X_{A}}\\ \^{X_{B}} ∙ \^{Y_{A}} & \^ { Y_{B}} ∙ \^{Y_{A}}& \^{Y_{B}} ∙ \^{Y_{A}}\\ \^{X_{B}} ∙ \^{Z_{A } } & \^{Y_{B}} ∙ \^{Z_{A}} & \^{Z_{B}} ∙ \^{Z_{A}} \end{array} \rightBあR=(あバツB^あYB^あZB^)=
バツB^∙バツあ^バツB^∙Yあ^バツB^∙Zあ^YB^∙バツあ^YB^∙Yあ^YB^∙Zあ^ZB^∙バツあ^YB^∙Yあ^ZB^∙Zあ^
今理解した行列の本質によれば、XA ^ \^{X_{A}}バツあ^行列で写像された後、単位ベクトルXB ^ \^{X_{B}}になります。バツB^在XA ^, YA ^, ZA ^ \^{X_{A}}, \^{Y_{A}}, \^{Z_{A}}バツあ^、Yあ^、Zあ^3 つの基底ベクトルへの射影は、合成後は正確に XB になります ^ \^{X_{B}}バツB^;や ^ \^{Y_{A}}Yあ^行列で写像された後、単位ベクトルYB ^ \^{Y_{B}}になります。YB^在XA ^, YA ^, ZA ^ \^{X_{A}}, \^{Y_{A}}, \^{Z_{A}}バツあ^、Yあ^、Zあ^3 つの基底ベクトルへの射影は、合成後は正確に YB になります ^ \^{Y_{B}}YB^;ざ ^ \^{Z_{A}}Zあ^行列で写像された後、単位ベクトルZB ^ \^{Z_{B}}になります。ZB^在XA ^, YA ^, ZA ^ \^{X_{A}}, \^{Y_{A}}, \^{Z_{A}}バツあ^、Yあ^、Zあ^3 つの基底ベクトルへの射影は、合成後は正確に ZB になります ^ \^{Z_{B}}ZB^、この回転行列は実際には座標系A {A}ですAの空間変換により、座標系B {B}B
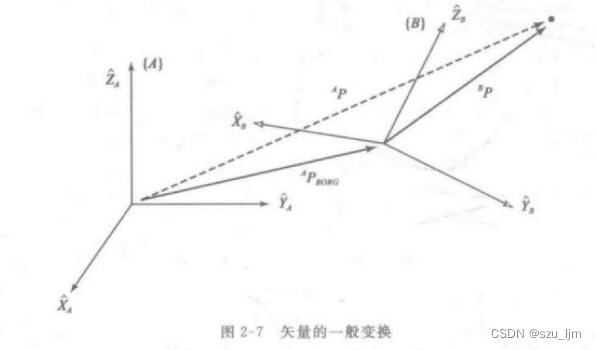
B{B}とB座標系の姿勢。位置ベクトルAPBORG ^{A}{P_{BORG}} が必要です。AP _ボーグB{B}を決定するA{A}を基準としたB座標系A座標系の相対位置は最終的にB{B}B座標系
B = BAR , APBORG {B} = {
{_{B}^{A}R, ^{A}{P_{BORG}}}} となります。B=BあR 、あPボーグ
3 次元空間における 2 つの座標系のポーズ表現を学習した後、座標系A {A}について説明します。AのベクトルはB{B}Bで表されるようにA {A}AにベクトルPPP、行列のマッピング原理によると、位置ベクトルPPPは座標系A{A}Aの式はPP座標系B{B}のP座標系B{B}からのBの式B は座標系A{A}A
AP = BPBAR ^{A}P = ^{B}P_ {B}^{A}RAP _=BPBあR

2 つの座標系の原点が一致しない場合は、2 つの座標系の原点の位置ベクトルAPBORG ^{A}{P_{BORG}}も考慮する必要があります。AP _ボーグ、APBORGより^{A}{P_{BORG}}AP _ボーグ座標系A {A}内にありますAは参照用に与えられているため、座標系マッピングの必要はなく、ベクトルを直接追加するだけです。
AP = BPBAR + APBORG ^{A}P = ^{B}P_{B}^{A}R + ^{A}{P_{BORG}}AP _=BPBあR+あPボーグ
次に紹介するのは4×4です同次変換行列上記の式を置き換えるこの式は、より明確かつ簡潔です
[ AP 1 ] = [ BARAPBORG [ 0 0 0 ] 1 ] [ BP 1 ] \left[ \begin{array}{ccc} ^{A}P\\ 1 \\ \end{array} \right ] = \left[ \begin{array}{ccc} _ {B}^{A}R & ^{A}{P_{BORG}}\\ \left[ \begin{配列{ccc} 0& 0 & 0\\ \end{配列} \right ] & 1\\ \end{配列} \right ]\left[ \begin{array}{ccc} ^{B}P \\ 1 \end{配列} \right ][AP _1]=[BあR[000]AP _ボーグ1][BP _1]
2. オイラー角と四元数
飛行機の質量中心に座標系B{B}を持つ飛行機を想像してみてください。B、座標系B{B}BのZZ付近Z軸回転α \alpha角度α 、その周りのYYY軸回転β \betaβ角、最後にその周りを○○するX軸回転γ \gammaγ角、この回転3つの角度の集合をオイラー角といいます。オイラー角にはヨー(ヨー角)、ピッチ(ピッチ角)、ロール(ロール角)の 3 つがあり、Z/Y/X 軸を中心とした回転角度を表します。
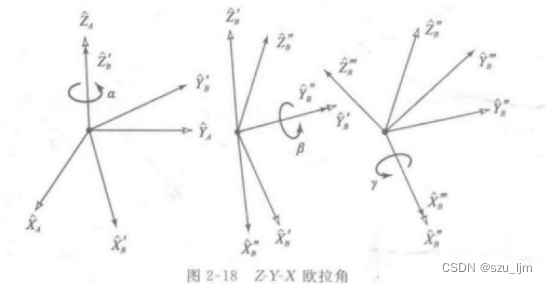
上記のオイラー角を形成するプロセスに従って、
回転の原理を組み合わせることで、各回転の数式 RZ ( α ) = [ cos ( α ) − sin ( α ) 0 sin ( α ) cos ( α ) 0 ] を与えることができます。行列 0 0 1 ] R_{Z}(\alpha) = \left[ \begin{array}{ccc} cos(\alpha) & -sin(\alpha) & 0\\ sin(\alpha) & cos(\アルファ )& 0\\ 0 &0 & 1 \end{配列} \right ]RZ( a )=
cos ( α )( a )の_0− ( a )内のscos ( α )0001
RY ( β ) = [ cos ( β ) 0 sin ( β ) 0 1 0 − sin ( β ) 0 cos ( β ) ] R_{Y}(\beta) = \left[ \begin{array}{ccc} cos (\beta) & 0 & sin(\beta)\\ 0 & 1& 0\\ -sin(\beta) &0 & cos(\beta) \end{array} \rightRや( b )=
cos ( b )0− ( b )のs010( b )の_0cos ( b )。
RX ( γ ) = [ 1 0 0 0 cos ( γ ) − sin ( γ ) 0 sin ( γ ) cos ( γ ) ] R_{X}(\gamma) = \left[ \begin{array}{ccc} & 0 & 0\\ 0 & cos(\gamma)& -sin(\gamma)\\ 0 &sin(\gamma) & cos(\gamma) \end{array} \rightR×( c )=
1000cos ( c )( c )の_0− ( c )のscos ( c )。
最後に、3 つの回転行列の積を積分して、座標系B {B}を取得します。一連の回転後にBによって形成される新しい座標系B ' {B^{'}}B'、回転行列B ' BR ^{B}_{B^{'}}R をB』B座標系B{B}を表すRBを座標系B ' {B^{'}}B'マップ関係
B ' BRZ − Y − X ( α , β , γ ) = [ cos ( α ) cos ( β ) cos ( α ) sin ( β ) sin ( γ ) − sin ( α ) cos ( γ ) cos ( α ) sin ( β ) cos ( γ ) + sin ( α ) sin ( γ ) sin ( α ) cos ( β ) sin ( α ) sin ( β ) sin ( γ ) + cos ( α ) cos ( γ ) sin ( α ) sin ( β ) cos ( γ ) − cos ( α ) sin ( γ ) − sin ( β ) cos ( β ) sin ( γ ) cos ( β ) cos ( γ ) ] ^{B}_{B^{'}} R_{ZYX} (\alpha,\beta,\gamma )= \left[ \begin{array}{ccc} cos(\alpha)cos(\beta) & cos(\alpha)sin(\beta)sin(\ gamma)-sin(\alpha)cos(\gamma) & cos(\alpha)sin(\beta)cos(\gamma)+sin(\alpha)sin(\gamma)\\ sin(\alpha)cos(\ beta) & sin(\alpha)sin(\beta)sin(\gamma)+cos(\alpha)cos(\gamma)& sin(\alpha)sin(\beta)cos(\gamma)-cos(\alpha )sin(\gamma)\\ -sin(\beta) &cos(\beta)sin(\gamma) & cos(\beta)cos(\gamma) \end{array} \rightB』BRZ − Y − X( 、_b 、c )=
cos ( a ) cos ( b )s in ( a ) cos ( b )− ( b )のscos ( a ) s in ( b ) s in ( c )−s in ( a ) cos ( c )( a )のs ( b )のs ( c ) _ _+cos ( a ) cos ( c )cos ( b ) s in ( c )cos ( a ) s in ( b ) cos ( c )+( a )のs ( c ) _ _s in ( a ) s in ( b ) cos ( c )−cos ( a ) s in ( c )cos ( b ) cos ( c )
クォータニオンは複素数に似ています。クォータニオンは実際には基底( a , i ⃗ , j ⃗ , k ⃗ ) {(a,\vec{i},\vec{j},\vec{k})} を表します。( 、_私、j、k)は、スカラーと 3x1 ベクトルの線形結合です。四元数のアナロジーとして複素数を使用します。四元数のスカラーは複素数の実数部であり、四元数のベクトルは複素数の虚数部です。の乗算は
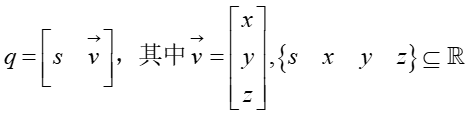
次のプロパティに従い、乗算自体は -1 であり、他の乗算および相互乗算のプロパティと同様に、右手の法則に従います。
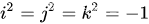
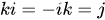
q \mathbf{q}を定義しますqは単位四元数で、 q = w + xi + yj + zk \mathbf{q} = w +xi +yj+zkとして表現できます。q=w+x i+y j+z k、q \mathbf{q}qは単位四元数です
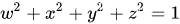
クォータニオンq \mathbf{q}qの回転行列 R\mathbf{R}_{\mathbf{q}}Rq次のように表現できます
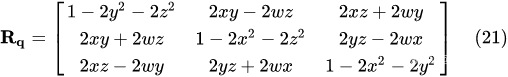
2. ROS の Python は座標変換を実装します
1. メッセージメッセージキャリアの調整
サブスクリプション公開モデルのデータ キャリア メッセージは重要な実装リンクです。座標変換の実現で一般的に使用される座標データ メッセージ キャリア メッセージには、geometry_msgs/TransformStamped および geometry_msgs/PointStamped が含まれます。
以下は geometry_msgs/TransformStamped メッセージによって返されたデータの一部であり、2 つの座標系間の姿勢関係を取得できます。通常、ここでは親座標系としてワールド座標系「world」を選択します。
std_msgs/Header header #头信息
uint32 seq #|-- 序列号
time stamp #|-- 时间戳
string frame_id #|-- 坐标 ID
string child_frame_id #子坐标系的 id
geometry_msgs/Transform transform #坐标信息
geometry_msgs/Vector3 translation #偏移量
float64 x #|-- X 方向的偏移量
float64 y #|-- Y 方向的偏移量
float64 z #|-- Z 方向上的偏移量
geometry_msgs/Quaternion rotation #四元数
float64 x
float64 y
float64 z
float64 w
以下は、geometry_msgs/PointStamped メッセージによって返されるデータの一部です。これが属する座標系内の点の位置を決定できます。
std_msgs/Header header #头信息
uint32 seq #|-- 序号
time stamp #|-- 时间戳
string frame_id #|-- 所属坐标系的 id
geometry_msgs/Point point #点坐标
float64 x #|-- x y z 坐标
float64 y
float64 z
これらのメッセージ データを使用すると、シミュレーション環境でタートルを追跡するなど、いくつかの楽しく強力な機能を実装できます。
2. カメが従うプログラムの実装
タートルの次の実装の中核は、タートル A と B の両方がワールド座標系を基準とした座標情報を公開し、その後この情報をサブスクライブして、B の座標系を基準とした A の情報を変換して取得する必要があることです。最後に線速度と角速度の情報を生成し、タートルBSportsを制御します。
まず、ワークスペースの src ディレクトリで、Catkin パッケージの作成オプションを選択して新しい関数パッケージを作成し、tf2、tf2_ros、tf2_geometry_msgs、roscpp rospy std_msgs依存パッケージを待ってから、Python ファイルを保存する新しいスクリプト フォルダーを作成し、起動ファイルを保存する起動フォルダーを作成します。
まず、ROS のサービスを呼び出して 2 番目の小さなタートルを生成します。2 番目のタートルを作成するには、rosservice を使用する必要があります。トピックは /spawn です。
#! /usr/bin/env python
#1.导包
import rospy
from turtlesim.srv import Spawn, SpawnRequest, SpawnResponse
if __name__ == "__main__":
# 2.初始化 ros 节点
rospy.init_node("turtle_spawn_p")
# 3.创建服务客户端
client = rospy.ServiceProxy("/spawn",Spawn)
# 4.等待服务启动
client.wait_for_service()
# 5.创建请求数据
req = SpawnRequest()
req.x = 1.0
req.y = 1.0
req.theta = 0
req.name = "turtle2"
# 6.发送请求并处理响应
try:
response = client.call(req)
rospy.loginfo("乌龟创建成功,名字是:%s",response.name)
except Exception as e:
rospy.loginfo("服务调用失败....")
次に、座標メッセージ トピック パブリッシング ノードを記述する必要があります。トピック/turtle name/pose/turtle name/poseを渡します。/タートル名/ポーズタートルのポーズを取得し、それを世界座標系を基準とした座標メッセージに解決して公開します。
#! /usr/bin/env python
# 1.导包
import rospy
import sys
from turtlesim.msg import Pose
from geometry_msgs.msg import TransformStamped
import tf2_ros
import tf_conversions
turtle_name = ""
def doPose(pose):
# rospy.loginfo("x = %.2f",pose.x)
#1.创建坐标系广播器
broadcaster = tf2_ros.TransformBroadcaster()
#2.将 pose 信息转换成 TransFormStamped
tfs = TransformStamped()
tfs.header.frame_id = "world"
tfs.header.stamp = rospy.Time.now()
tfs.child_frame_id = turtle_name
tfs.transform.translation.x = pose.x
tfs.transform.translation.y = pose.y
tfs.transform.translation.z = 0.0
qtn = tf_conversions.transformations.quaternion_from_euler(0, 0, pose.theta)
tfs.transform.rotation.x = qtn[0]
tfs.transform.rotation.y = qtn[1]
tfs.transform.rotation.z = qtn[2]
tfs.transform.rotation.w = qtn[3]
#3.广播器发布 tfs
broadcaster.sendTransform(tfs)
if __name__ == "__main__":
# 2.初始化 ros 节点
rospy.init_node("sub_tfs_p")
# 3.解析传入的命名空间
rospy.loginfo("-------------------------------%d",len(sys.argv))
if len(sys.argv) < 2:
rospy.loginfo("请传入参数:乌龟的命名空间")
else:
turtle_name = sys.argv[1]
rospy.loginfo("///乌龟:%s",turtle_name)
rospy.Subscriber(turtle_name + "/pose",Pose,doPose)
# 4.创建订阅对象
# 5.回调函数处理订阅的 pose 信息
# 5-1.创建 TF 广播器
# 5-2.将 pose 信息转换成 TransFormStamped
# 5-3.发布
# 6.spin
rospy.spin()
最後に、turtle1 と Turtle2 の TF 座標ブロードキャスト情報をサブスクライブすることによって、座標メッセージ トピック サブスクリプション ノードを作成する必要があります。最新の TF 座標情報を検索して変換し、turtle1 を Turtle2 を基準とした座標に変換し、線速度と角度を計算します。速度を取得してタートルの動作制御トピックに公開します
#! /usr/bin/env python
# 1.导包
import rospy
import tf2_ros
from geometry_msgs.msg import TransformStamped, Twist
import math
if __name__ == "__main__":
# 2.初始化 ros 节点
rospy.init_node("sub_tfs_p")
# 3.创建 TF 订阅对象
buffer = tf2_ros.Buffer()
listener = tf2_ros.TransformListener(buffer)
# 4.处理订阅到的 TF
rate = rospy.Rate(10)
# 创建速度发布对象
pub = rospy.Publisher("/turtle2/cmd_vel",Twist,queue_size=1000)
while not rospy.is_shutdown():
rate.sleep()
try:
#def lookup_transform(self, target_frame, source_frame, time, timeout=rospy.Duration(0.0)):
trans = buffer.lookup_transform("turtle2","turtle1",rospy.Time(0))
# rospy.loginfo("相对坐标:(%.2f,%.2f,%.2f)",
# trans.transform.translation.x,
# trans.transform.translation.y,
# trans.transform.translation.z
# )
# 根据转变后的坐标计算出速度和角速度信息
twist = Twist()
# 间距 = x^2 + y^2 然后开方
twist.linear.x = 0.5 * math.sqrt(math.pow(trans.transform.translation.x,2) + math.pow(trans.transform.translation.y,2))
twist.angular.z = 4 * math.atan2(trans.transform.translation.y, trans.transform.translation.x)
pub.publish(twist)
except Exception as e:
rospy.logwarn("警告:%s",e)
ターミナルのPythonファイルに実行権限を追加します。
chmod +777 *.py
前回のメモの方法に従って CMakeLists.txt ファイルを設定します。3 つの .py ファイルをコンパイルして宣言し、catkin_make:build を実行してコンパイル後にエラーがあるかどうかを確認します。エラーがない場合は、起動ファイル。
<launch>
<node pkg="turtlesim" type="turtlesim_node" name="turtle1" output="screen" />
<node pkg="turtlesim" type="turtle_teleop_key" name="key_control" output="screen"/>
<node pkg="xxx" type="xxx.py" name="turtle_spawn" output="screen"/>
<node pkg="xxx" type="xxx.py" name="tf_pub1" args="turtle1" output="screen"/>
<node pkg="xxx" type="xxx.py" name="tf_pub2" args="turtle2" output="screen"/>
<node pkg="xxx" type="xxx.py" name="tf_sub" output="screen"/>
</launch>
起動ファイルを作成した後、起動ファイルを右クリックしてターミナルを開き、起動ファイルを実行して次のタートルの効果を確認します。
roslaunch xxx(功能包) xxx.launch(launch文件)
要約する
以上はロボット座標変換の学習ノートであり、ロボット座標変換の理論的基礎と、ROS における TF 座標変換の実装プロセスを簡単に紹介します。ロボットの座標変換の重要性は、ロボットが異なる座標系でも一貫した動作精度を維持できることです。座標系が異なるとロボットの軌道や位置情報が変化するためです。例えば、ベース座標系におけるロボットの動作は直線運動であるが、ツール座標系における動作は回転運動である場合がある。座標変換を行わないとロボットの軌道や位置情報がずれてしまい、ロボットが正確に作業を完了できなくなります。