【VARモデル | 時系列】ヘルプドキュメント：VARモデルの紹介とPythonの実践（ソースコード含む）

ベクトル自己回帰 (VAR) は、複数の時系列間の線形相互依存性を把握するために使用される確率プロセス モデルです。VAR モデルは、複数の進化変数を考慮して、単変量自己回帰モデル (AR モデル) を一般化します。

VAR のすべての変数は、同じ方法でモデルに入力されます。各変数には、それ自身のラグ値、他のモデル変数のラグ値、および誤差項に関して進化を説明する方程式があります。

1.はじめに

まず、Vector AutoRegression (VAR) とは何ですか? また、いつ使用するのでしょうか?

ベクトル自己回帰 (VAR) は、2 つ以上の時系列が相互作用するときに使用される多変量予測アルゴリズムです。

つまり、VAR を使用するための基本的な要件は次のとおりです。

1. 少なくとも 2 つの時系列 (変数) が必要です。
2. 時系列は互いに影響を与えるはずです。

良い。では、なぜ「自己回帰」と呼ばれるのでしょうか。

各変数 (時系列) は過去の値の関数としてモデル化されるため、自己回帰モデルと見なされます。つまり、予測変数は系列のラグ (時間遅延値) にすぎません。

では、VAR は、AR、ARMA、ARIMA などの他の自己回帰モデルとどう違うのでしょうか?

主な違いは、これらのモデルが一方向であり、予測子が Y に影響を与え、その逆であることです。一方、Vector Auto-Regression (VAR) は双方向です。つまり、変数は相互に影響を及ぼします。

2. VAR モデル式の背後にある直感

自己回帰モデルでは、時系列はそれ自体のラグの線形結合としてモデル化されます。つまり、シリーズの過去の値を使用して、現在と未来を予測します。

一般的な AR(p) モデルの方程式は次のようになります。

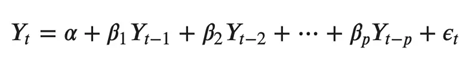
ここで、α は定数である切片であり、β1、β2 から βp は Y から次数 p までのラグの係数です。次数 "p" は、Y の最大 p ラグが使用されることを意味し、これが方程式の予測子です。ε_{t} は誤差で、ホワイト ノイズとして扱われます。

良い。では、VAR モデルの公式はどのようなものでしょうか?

VAR モデルでは、各変数は、それ自体の過去の値とシステム内の他の変数の過去の値の線形結合としてモデル化されます。相互に作用する複数の時系列があるため、変数 (時系列) ごとに 1 つの方程式の連立方程式としてモデル化されます。

つまり、相互に作用する 5 つの時系列がある場合、5 つの方程式のシステムができます。

では、方程式はどのように正確に構築されるのでしょうか。

2 つの変数 (時系列) Y1 と Y2 があり、時間 (t) でのこれらの変数の値を予測する必要があるとします。

Y1(t)を計算するために、VARはY1とY2の過去の値を使用します。同様に、Y2(t) を計算するには、Y1 と Y2 の過去の値を使用します。

たとえば、2 つの時系列 (変数 "Y1" と "Y1") を持つ VAR(2) モデルの方程式系は次のようになります。

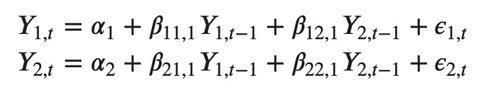
ここで、Y{1, t-1} と Y{2, t-1} は、それぞれ時系列 Y1 と Y2 の最初のラグです。

上記の方程式は VAR(1) モデルと呼ばれます。これは、各方程式が次数 1 であるためです。つまり、予測変数 (Y1 および Y2) の最大 1 つのラグが含まれます。

式の Y 項は相関しているため、Y は外生予測変数ではなく内生変数と見なされます。

同様に、2 変数の 2 次 VAR(2) モデルには、変数ごとに最大 2 つのラグ (Y1 と Y2) が含まれます。

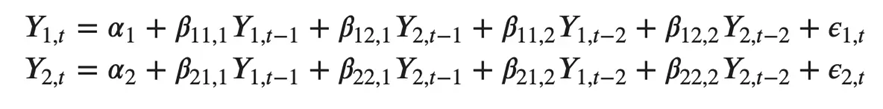
3 つの変数 (Y2、Y1、Y2) を持つ 2 次 VAR(3) モデルは次のようになると想像できます。

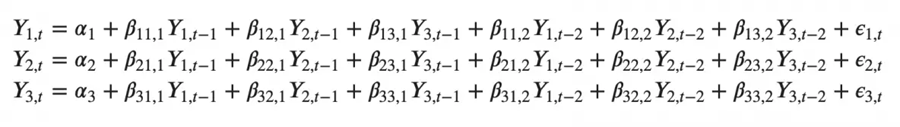
モデル内の時系列 (変数) の数が増えると、連立方程式は大きくなります。

3. Python で VAR モデルを構築する

VAR モデルを構築するプロセスには、次の手順が含まれます。

1. 時系列機能の分析
2. 時系列間の因果関係のテスト
3. 定常性試験
4. 必要に応じてシーケンスを変換して静止させます
5. 最良の次数を見つける (p)
6. トレーニング データセットとテスト データセットを準備する
7. トレーニング モデル
8. ロールバック変換 (ある場合)
9. テスト セットを使用してモデルを評価する
10. 将来の予測

3.1 パッケージのインポート

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Import Statsmodels
from statsmodels.tsa.api import VAR
from statsmodels.tsa.stattools import adfuller
from statsmodels.tools.eval_measures import rmse, aic

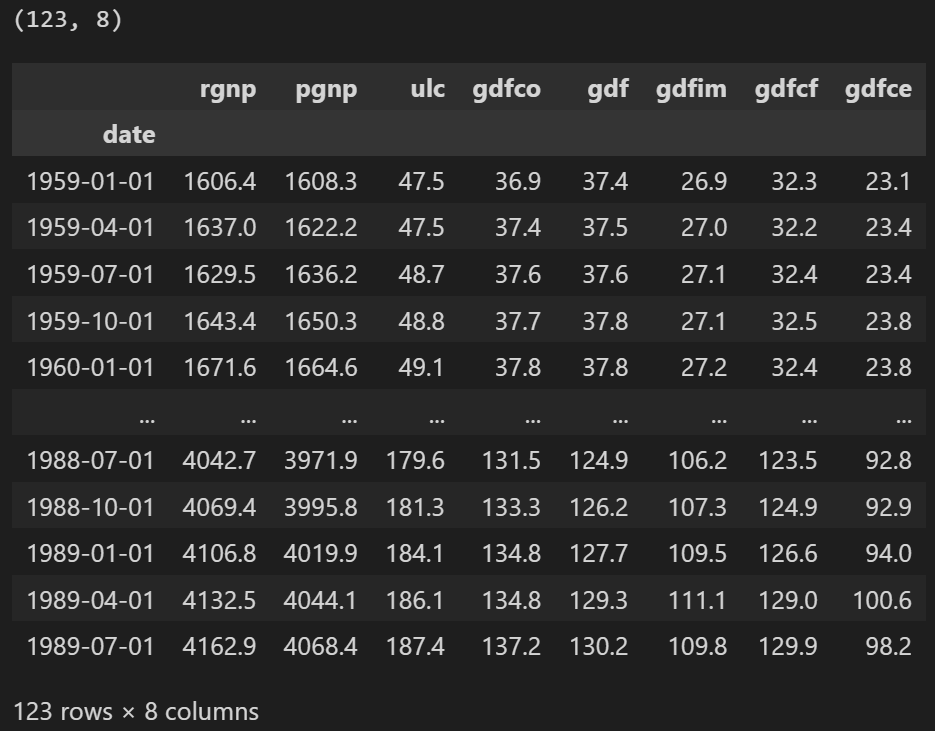
3.2 データセットのインポート

Yash P Mehra の 1994 年の記事 "The Wage Growth and Inflation Process: An Empirical Approach" で使用された時系列を使用します。

このデータセットには、次の 8 つの四半期時系列があります。

1. rgnp : 実質GNP. (実質国民総生産)
2. pgnp : 潜在実質GNP. (潜在実質国民総生産)
3. ulc : 単位労働コスト. (単位労働コスト)
4. gdfco ：食品・エネルギーを除く個人消費支出の固定加重デフレーター（食品・エネルギーを除く個人消費支出の固定加重デフレーター）
5. gdf : 固定加重 GNP デフレーター (固定加重国民総生産デフレーター)
6. gdfim : 固定重みインポート デフレーター (固定重みインポート デフレーター)
7. gdfcf : 個人消費支出における食品の固定重量デフレーター. (個人消費支出における食品の固定重量デフレーター)
8. gdfce : 個人消費支出におけるエネルギーの固定加重デフレーター. (個人消費支出におけるエネルギーの固定加重デフレーター)

filepath = 'https://raw.githubusercontent.com/selva86/datasets/master/Raotbl6.csv'
df = pd.read_csv(filepath, parse_dates = ['date'], index_col = 'date')
print(df.shape)
df

3.3 時系列の可視化

fig, axes = plt.subplots(nrows=4, ncols=2, dpi=120, figsize=(10,6))
for i, ax in enumerate(axes.flatten()):
    data = df[df.columns[i]]
    ax.plot(data, color='red', linewidth=1)
    # Decorations
    ax.set_title(df.columns[i])
    ax.xaxis.set_ticks_position('none')
    ax.yaxis.set_ticks_position('none')
    ax.spines["top"].set_alpha(0)
    ax.tick_params(labelsize=6)

plt.tight_layout()

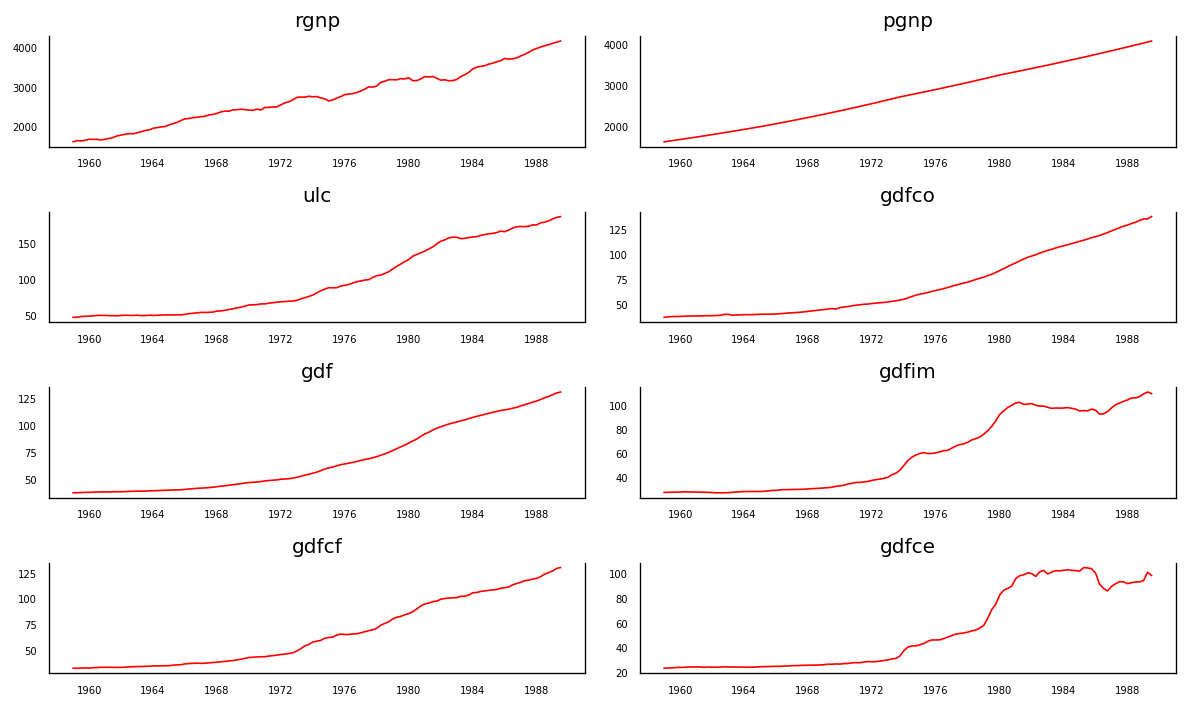
gdfim と gdfce を除いて、各シリーズは何年にもわたってかなり類似した傾向パターンを示しており、1980 年以降は異なるパターンが見られます。

OK、分析の次のステップは、これらのシーケンス間の因果関係を調べることです。グレンジャー因果関係検定と共和分検定は、この問題の解決に役立ちます。

3.4 グレンジャー因果性検定を用いた因果性の検定

ベクトル自己回帰の背後にある基礎は、システム内の各時系列が互いに影響を与えることです。つまり、シーケンスは、システム内の他のシーケンスと同様に、それ自体の過去の値を使用して予測できます。

グレンジャーの因果性テストを使用すると、モデルを構築する前にこの関係をテストすることもできます。

グレンジャーの因果関係は正確には何をテストしますか?

グレンジャー因果関係は、回帰式の過去の値の係数がゼロであるという帰無仮説を検定します。

簡単に言えば、時系列 (X) の過去の値は他の系列 (Y) にはつながりません。したがって、検定から得られた p 値が有意水準 0.05 未満の場合、帰無仮説を安全に棄却できます。

以下のコードは、特定のデータ フレーム内の時系列のすべての可能な組み合わせに対してグレンジャー因果関係テストを実装し、各組み合わせの p 値を出力行列に格納します。

from statsmodels.tsa.stattools import grangercausalitytests
maxlag = 12
test = 'ssr_chi2test'
def grangers_causation_matrix(data, variables, test='ssr_chi2test', verbose=False):    
    df = pd.DataFrame(np.zeros((len(variables), len(variables))), columns=variables, index=variables)
    for c in df.columns:
        for r in df.index:
            test_result = grangercausalitytests(data[[r, c]], maxlag=maxlag, verbose=False)
            p_values = [round(test_result[i+1][0][test][1],4) for i in range(maxlag)]
            if verbose: print(f'Y = {
      
      r}, X = {
      
      c}, P Values = {
      
      p_values}')
            min_p_value = np.min(p_values)
            df.loc[r, c] = min_p_value
    df.columns = [var + '_x' for var in variables]
    df.index = [var + '_y' for var in variables]
    return df

grangers_causation_matrix(df, variables = df.columns)   

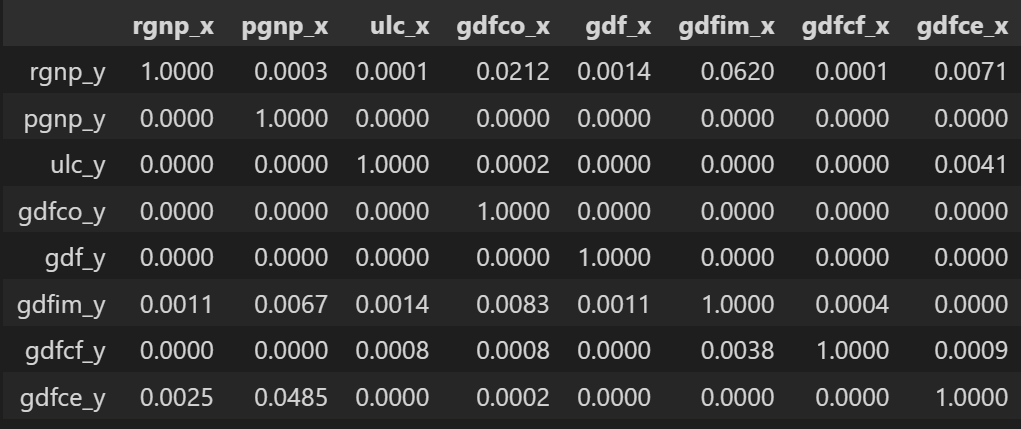
時系列のすべての可能な組み合わせについてグレンジャー因果関係をチェックします。行は応答変数で、列は予測変数です。

表中の値はP値です。有意水準 (0.05) 未満の P 値は、帰無仮説に対応する過去の値の係数がゼロであることを意味します。つまり、X は Y を引き起こさず、棄却することができます。

データ: 時系列変数を含む df データ フレーム

variables : 時系列変数の名前を含むリスト。

では、上記の出力をどのように読むのでしょうか? 行は応答 (Y)、列は予測変数 (X) のシーケンスです。

たとえば、(行 0、列 0003) の値 1.2 を取得すると、結果の p 値を参照します。また、(行 2、列 1) の 0.000 は、結果の p 値を指します。pgnp_x rgnp_y rgnp_y pgnp_x

では、p 値をどのように解釈すればよいでしょうか。

指定された p 値 < 有意水準 (0.05) の場合、対応する X シリーズ (列) は Y (行) になります。

たとえば、(行 1、列 2) の 0.0003 の p 値は、原因に対するグレンジャー因果関係検定の p 値を表し、有意水準 0.05 よりも小さいです。pgnp_x rgnp_y

したがって、帰無仮説を棄却し、その理由を結論付けることができます。pgnp_x rgnp_y

上の表の P 値を見ると、システム内のほぼすべての変数 (時系列) が交互に入れ替わっていることがわかります。

これにより、このような複数の時系列システムは、VAR モデルを使用した予測に適した候補になります。

次に、共和分検定を実行しましょう。

3.5 共和分検定

共和分検定は、2 つ以上の時系列間に統計的に有意な関係が存在するかどうかを判断するのに役立ちます。

しかし、共和分とはどういう意味ですか?

これを理解するには、まず「統合の順序」(d) とは何かを知る必要があります。

統合順序 (d) は、非定常時系列を静止させるために必要な差分の数に他なりません。

ここで、2 つ以上の時系列があり、それらの線形結合が存在し、その統合次数 (d) が単一の時系列の時系列よりも小さい場合、時系列のコレクションは共和分と呼ばれます。

良い？

2 つ以上の時系列が共和分している場合、長期的に統計的に有意な関係があることを意味します。

これは、ベクトル自己回帰 (VAR) モデルの基礎となる基本的な前提です。したがって、VAR モデルの構築を開始する前に、共和分検定を実装することは非常に一般的です。

わかりました、では、このテストをどのように行いますか?

参考文献：

https://www.jstor.org/stable/2938278?seq=1#page_scan_tab_contents

Python での実装は、次のように非常に簡単です。

from statsmodels.tsa.vector_ar.vecm import coint_johansen

def cointegration_test(df, alpha=0.05): 
    out = coint_johansen(df,-1,5)
    d = {
    
    '0.90':0, '0.95':1, '0.99':2}
    traces = out.lr1
    cvts = out.cvt[:, d[str(1 - alpha)]]
    def adjust(val, length = 6): return str(val).ljust(length)

    # Summary
    print('Name   ::  Test Stat > C(95%)    =>   Signif  \n', '--'*20)
    for col, trace, cvt in zip(df.columns, traces, cvts):
        print(adjust(col), ':: ', adjust(round(trace,2), 9), ">", adjust(cvt, 8), ' =>  ' , trace > cvt)

cointegration_test(df)

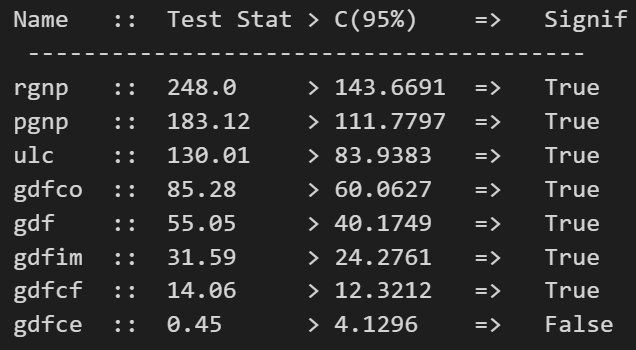
3.6 シーケンスをトレーニング データとテスト データに分割する

データセットをトレーニング データとテスト データに分割します。

VAR モデルが適合され、次の 4 つの観測値を予測するために使用されます。これらの予測は、テスト データの実際の値と比較されます。

比較のために、この記事で後述するように、いくつかの予測精度指標を使用します。

nobs = 4
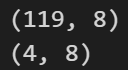
df_train, df_test = df[0:-nobs], df[-nobs:]

# Check size
print(df_train.shape)  # (119, 8)
print(df_test.shape)  # (4, 8)

3.7 定常性のチェックと時系列の定常性の維持

VAR モデルでは予測される時系列が定常的である必要があるため、システム内のすべての時系列の定常性をチェックするのが通例です。

繰り返しになりますが、定常時系列とは、時間の経過とともに特性 (平均や分散など) が変化しない時系列です。

では、どのように定常性をテストしますか?

ユニット ルート テストと呼ばれる一連のテストがあります。人気のあるものは次のとおりです。

1. 拡張ディッキー フラー テスト (ADF テスト)
2. KPSS テスト
3. フィリップ・ペレン検定

この目的のために ADF テストを使用してみましょう。

ちなみに、系列が非定常であることがわかった場合は、系列を一度微分し、定常になるまでテストを繰り返して定常にします。

差分は系列の長さを 1 減らし、すべての時系列は同じ長さでなければならないため、差分を選択する場合はシステム内のすべての系列を区別する必要があります。

理解しているようだ

ADF テストを実装してみましょう。

まず、任意の時系列の ADF テスト結果を書き出すナイス関数 ( ) を実装し、この関数を各系列に 1 つずつ実装します。adfuller_test()

def adfuller_test(series, signif=0.05, name='', verbose=False):
    """Perform ADFuller to test for Stationarity of given series and print report"""
    r = adfuller(series, autolag='AIC')
    output = {
    
    'test_statistic':round(r[0], 4), 'pvalue':round(r[1], 4), 'n_lags':round(r[2], 4), 'n_obs':r[3]}
    p_value = output['pvalue'] 
    def adjust(val, length= 6): return str(val).ljust(length)

    # Print Summary
    print(f'    Augmented Dickey-Fuller Test on "{
      
      name}"', "\n   ", '-'*47)
    print(f' Null Hypothesis: Data has unit root. Non-Stationary.')
    print(f' Significance Level    = {
      
      signif}')
    print(f' Test Statistic        = {
      
      output["test_statistic"]}')
    print(f' No. Lags Chosen       = {
      
      output["n_lags"]}')

    for key,val in r[4].items():
        print(f' Critical value {
      
      adjust(key)} = {
      
      round(val, 3)}')

    if p_value <= signif:
        print(f" => P-Value = {
      
      p_value}. Rejecting Null Hypothesis.")
        print(f" => Series is Stationary.")
    else:
        print(f" => P-Value = {
      
      p_value}. Weak evidence to reject the Null Hypothesis.")
        print(f" => Series is Non-Stationary.")

各シリーズを呼び出します。

# ADF Test on each column
for name, column in df_train.iteritems():
    adfuller_test(column, name=column.name)
    print('\n')

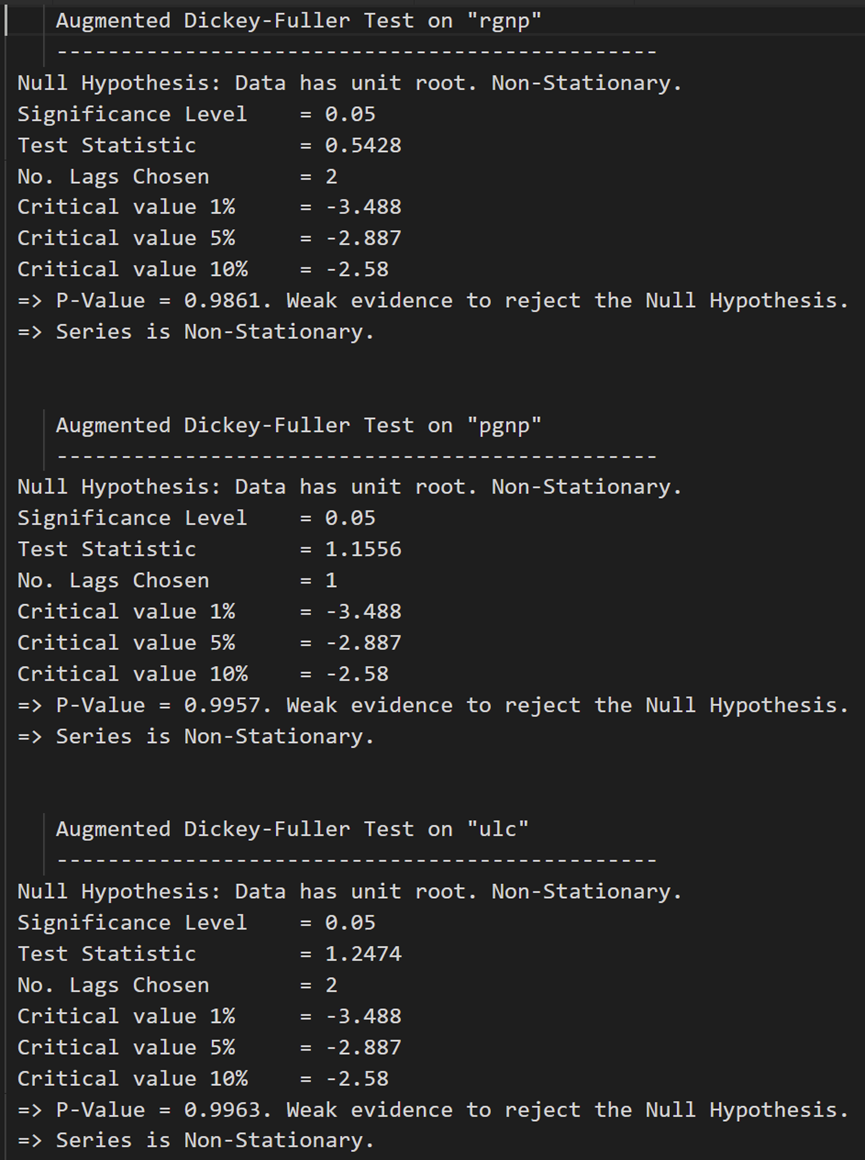
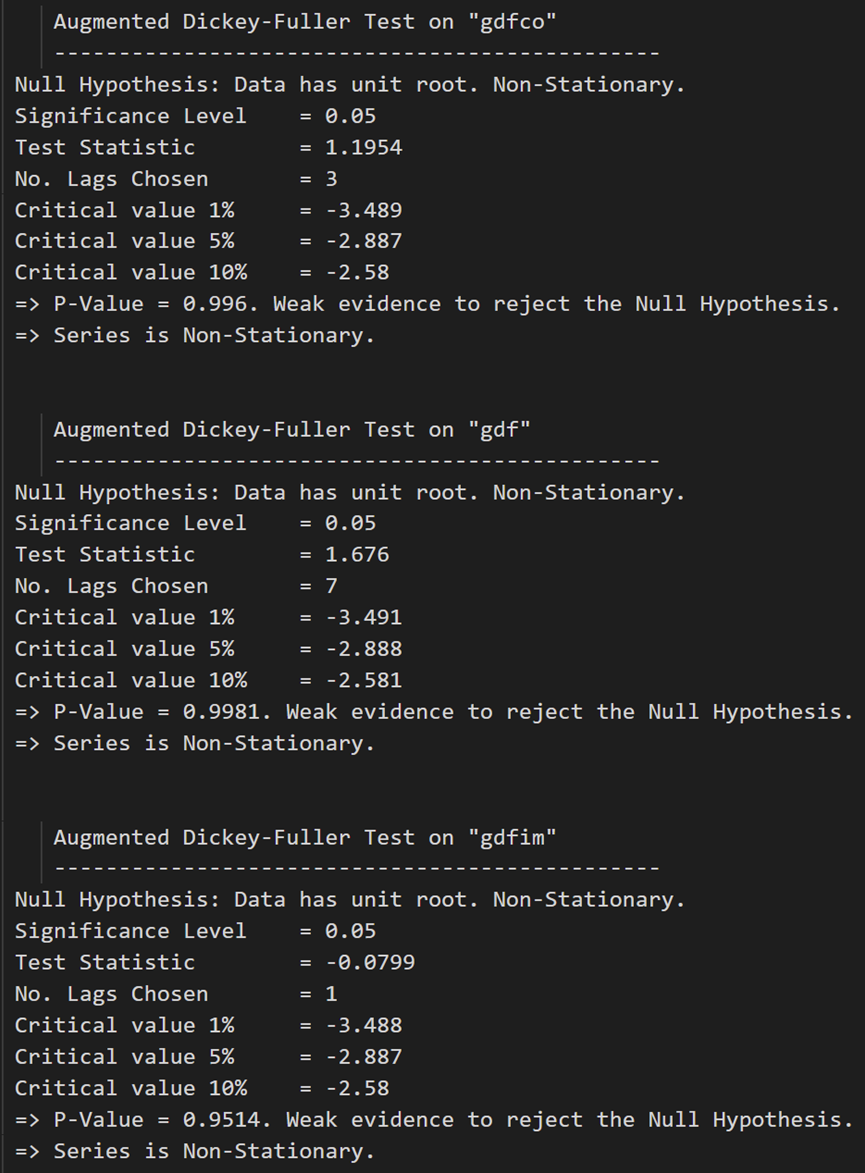
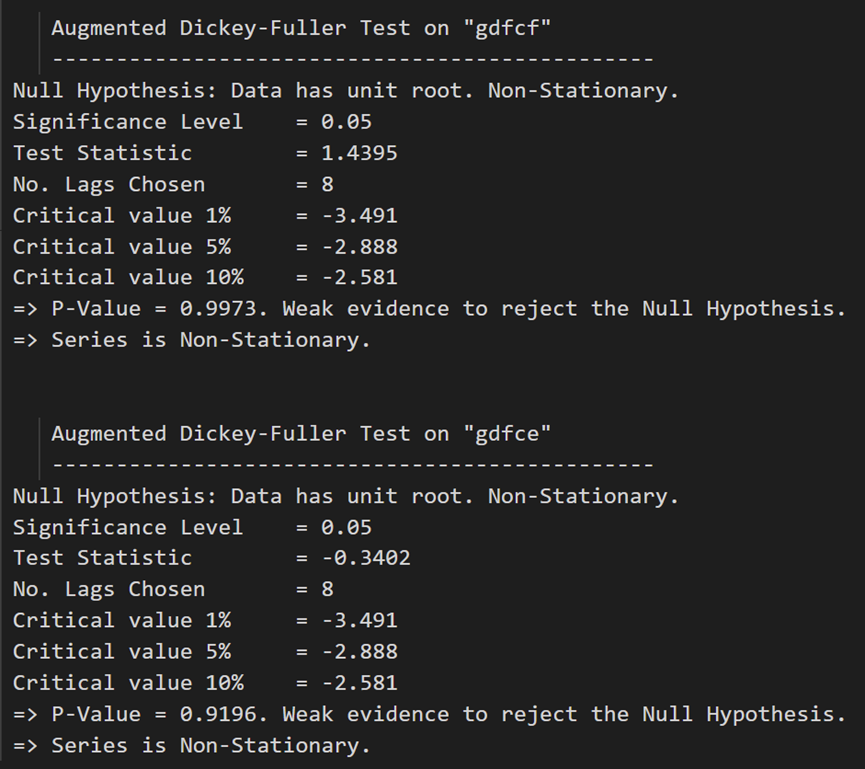
ADF テストは、どの時系列も定常でないことを確認します。それらすべてを一度差分して、もう一度確認しましょう。

# 1st difference
df_differenced = df_train.diff().dropna()

# ADF Test on each column of 1st Differences Dataframe
for name, column in df_differenced.iteritems():
    adfuller_test(column, name=column.name)
    print('\n')

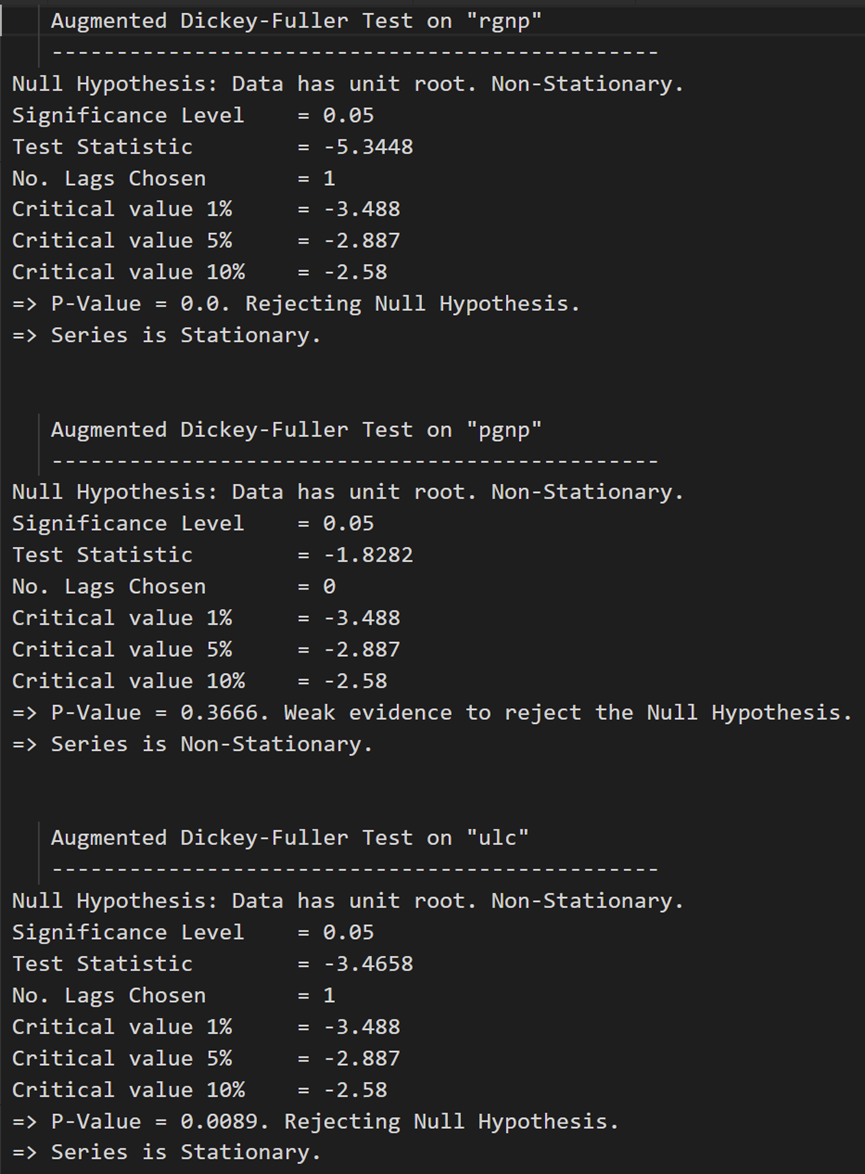
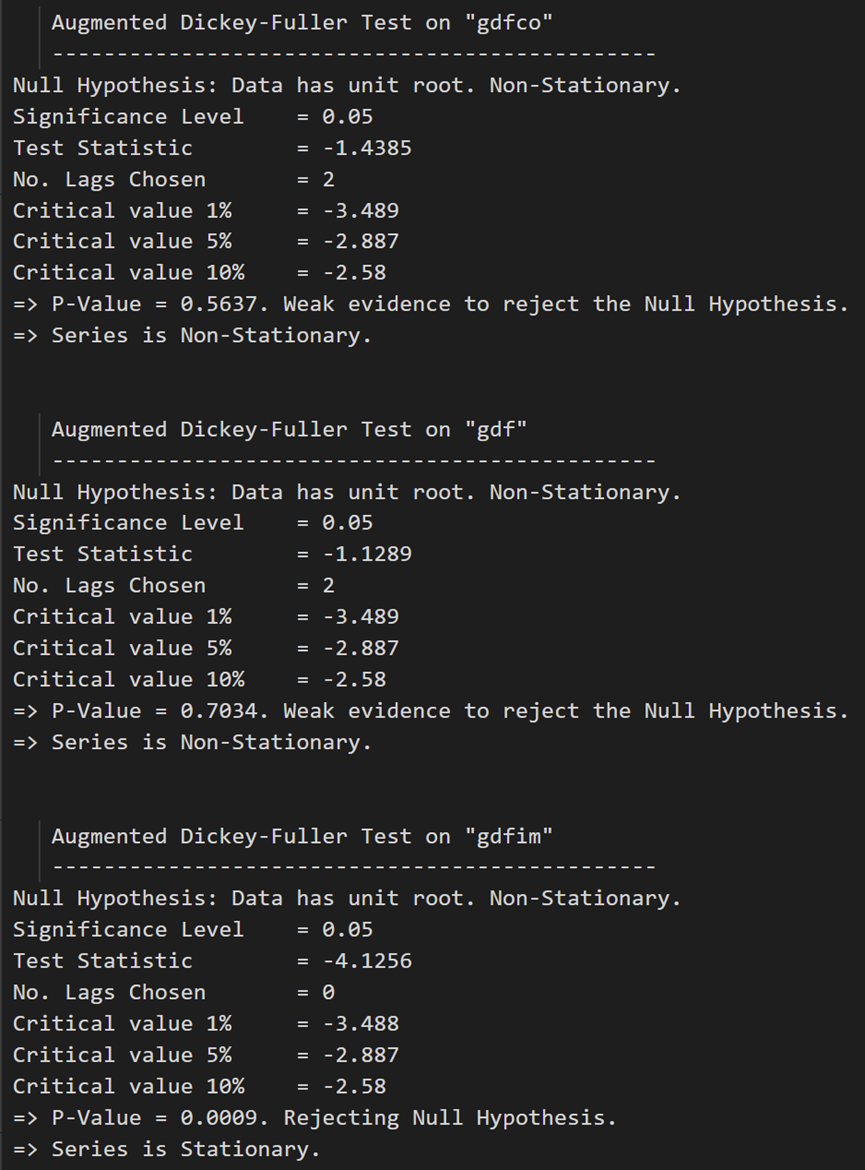
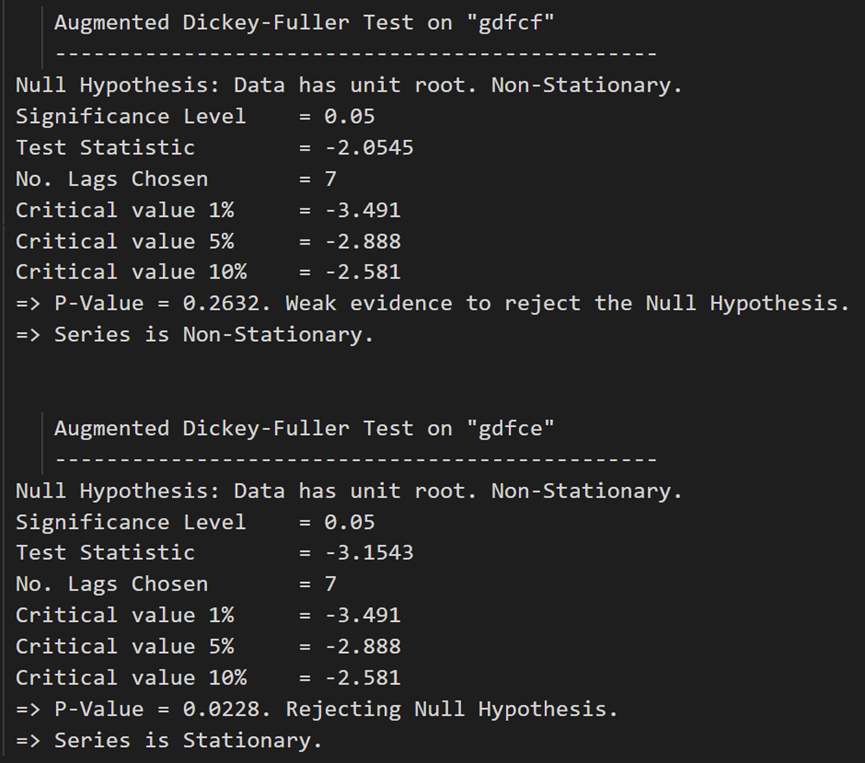
最初の差異の後、実質賃金 (製造業) は依然として静的ではありません。その臨界値は、5% から 10% の有意水準の間にあります。

VAR モデルのすべての系列は、同じ数の観測値を持つ必要があります。

したがって、2 つのオプションのうちの 1 つが残されています。

つまり、最初の差分シリーズを続行するか、すべてのシリーズを再度差分します。

# Second Differencing
df_differenced = df_differenced.diff().dropna()

ADF テストを再度実行します。

# ADF Test on each column of 2nd Differences Dataframe
for name, column in df_differenced.iteritems():
    adfuller_test(column, name=column.name)
    print('\n')

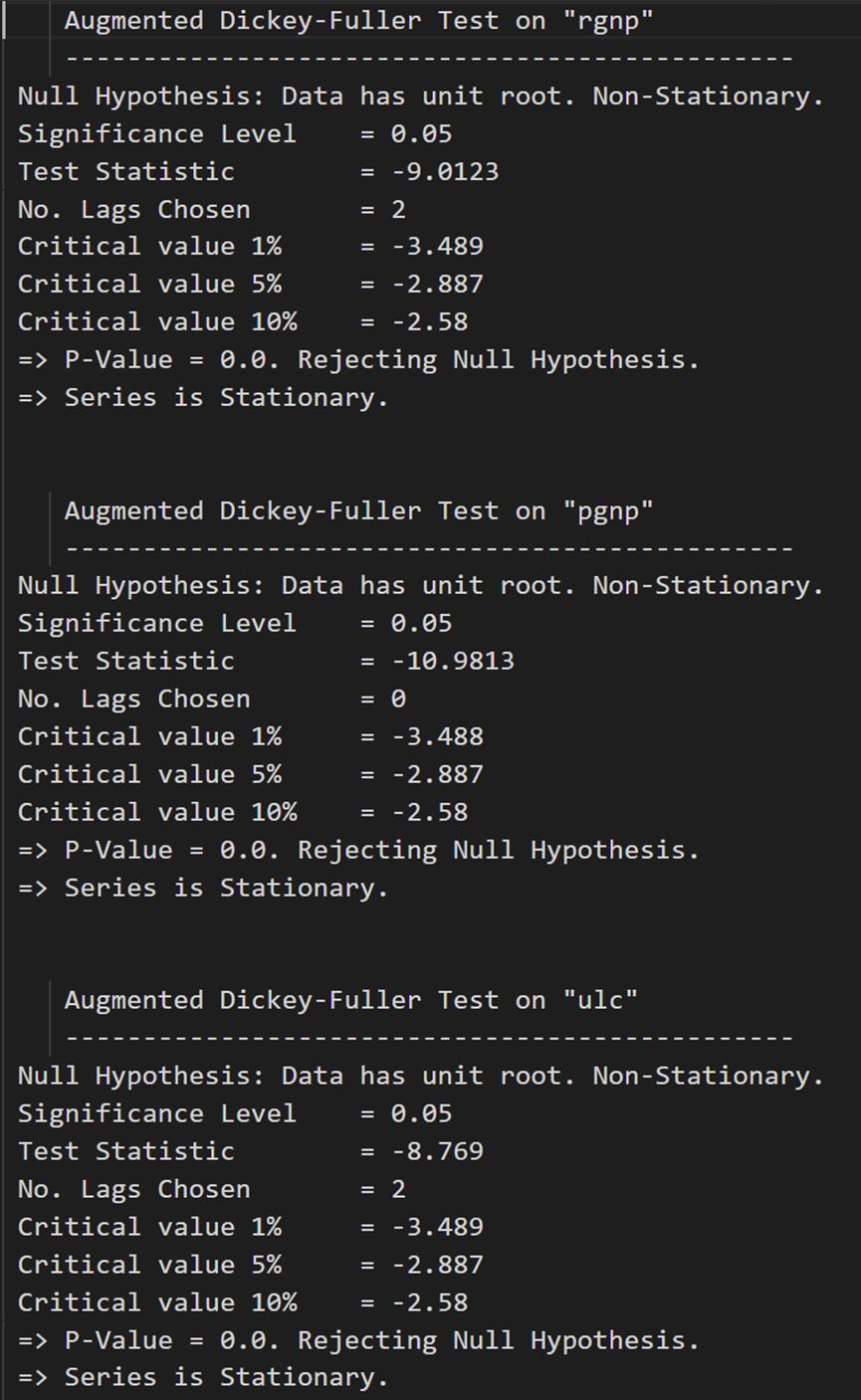
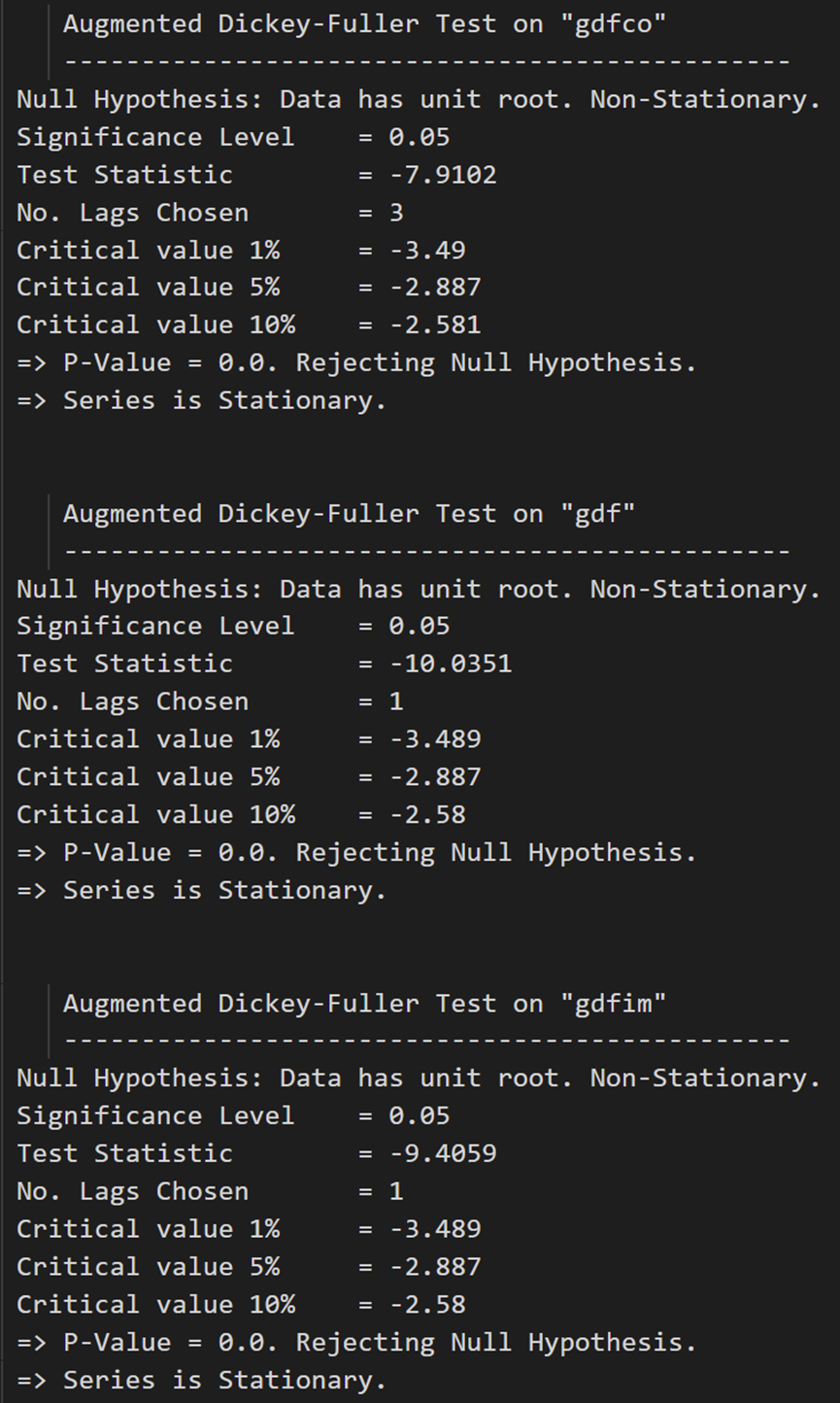
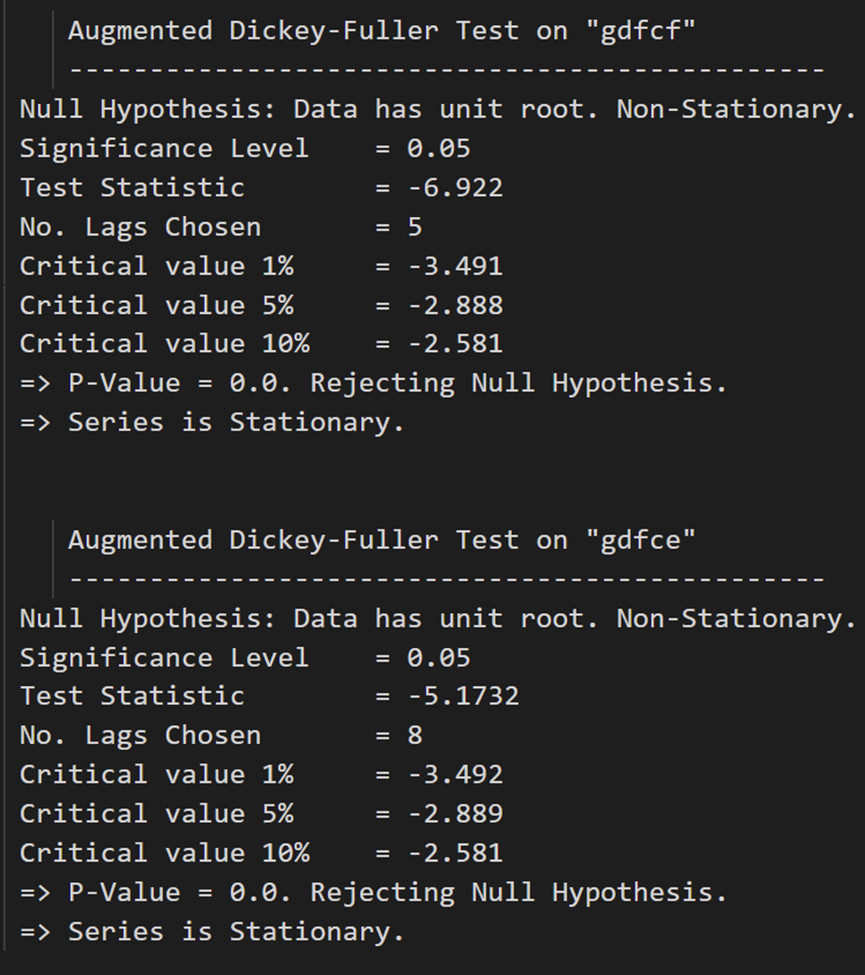
すべてのシリーズが静的になりました。

トレーニングとテストのデータセットを準備しましょう。

3.8 VAR モデルの次数の選び方 (P)

VAR モデルの正しい次数を選択するために、VAR モデルの次数を増やして繰り返し当てはめ、AIC モデルが最小になる次数を選択します。

AIC を見るのが一般的な方法ですが、BIC と FPE の他の最適な比較推定値を調べることもできます。

model = VAR(df_differenced)
for i in [1,2,3,4,5,6,7,8,9]:
    result = model.fit(i)
    print('Lag Order =', i)
    print('AIC : ', result.aic)
    print('BIC : ', result.bic)
    print('FPE : ', result.fpe)
    print('HQIC: ', result.hqic, '\n')

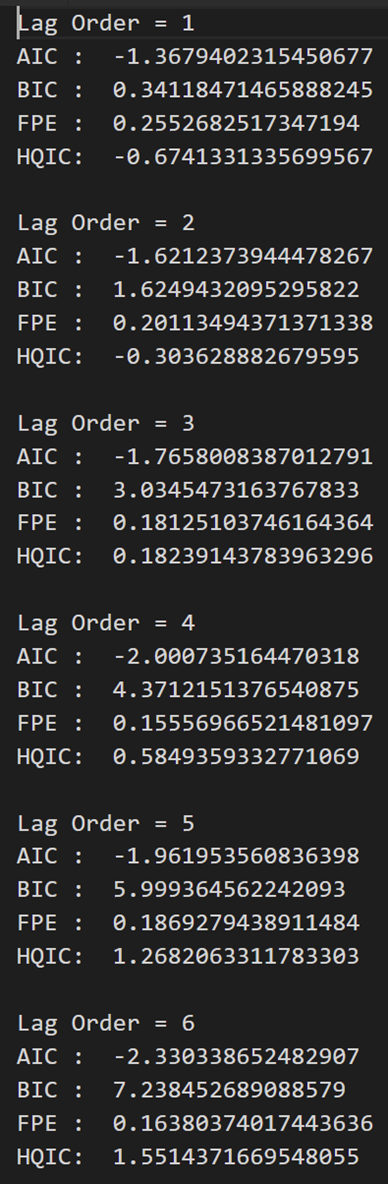
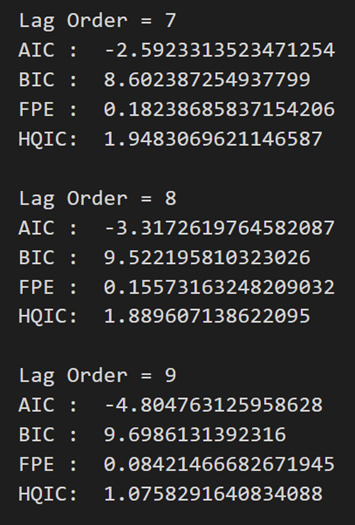
上記の出力では、AIC はラグ 4 で最小になり、ラグ 5 で増加し、さらに減少し続けます。

ラグ 4 モデルを使用してみましょう。

VAR モデルの次数 (p) を選択する別の方法は、この方法を使用することです。model.select_order(maxlags)

選択された順序 (p) は、「AIC」、「BIC」、「FPE」、および「HQIC」のスコアが最も低い順序です。

x = model.select_order(maxlags=12)
x.summary()

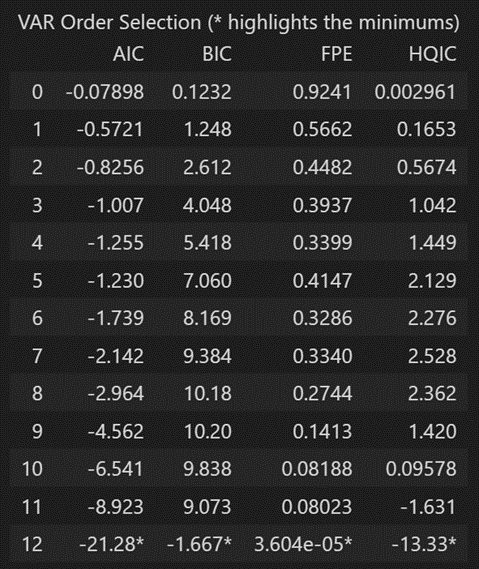
FPE および HQIC によると、ヒステリシスの大きさが 3 のときに最良のヒステリシスが観察されました。

ただし、観測された AIC と BIC の値が、使用したときに表示される値と異なる理由については説明がありません。

明示的に計算された AIC はラグ 4 で最も低いため、選択した次数を 4 に選択します。

3.9 選択した注文の VAR モデルのトレーニング (p)

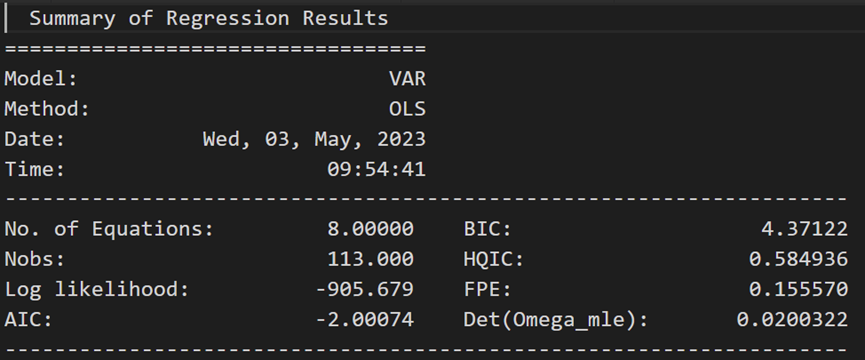
model_fitted = model.fit(4)
model_fitted.summary()

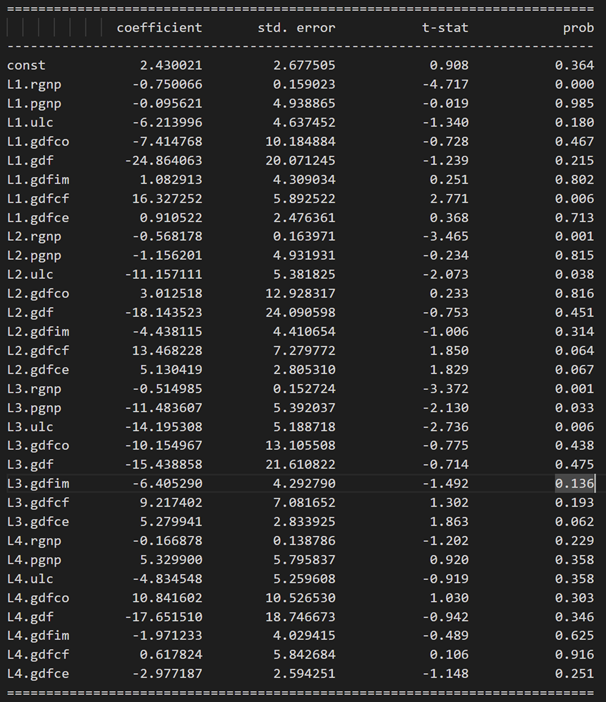
式 rgnp の結果：

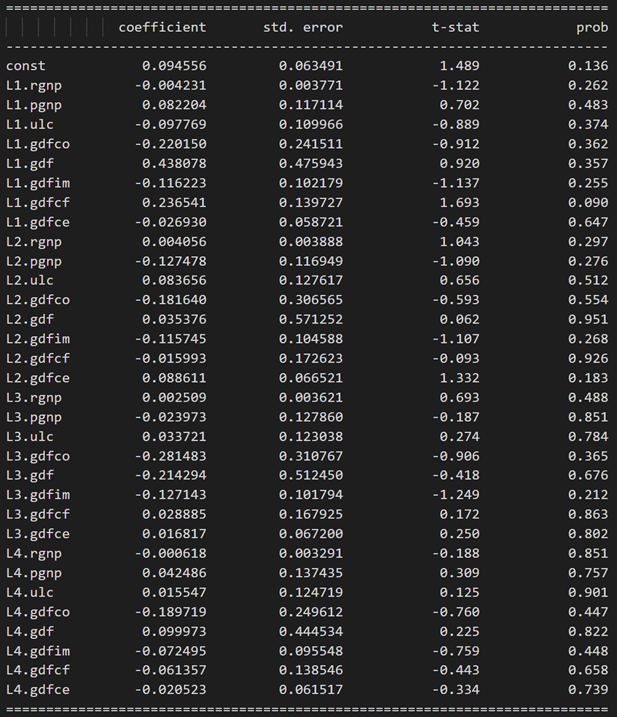
方程式 pgnp の結果：

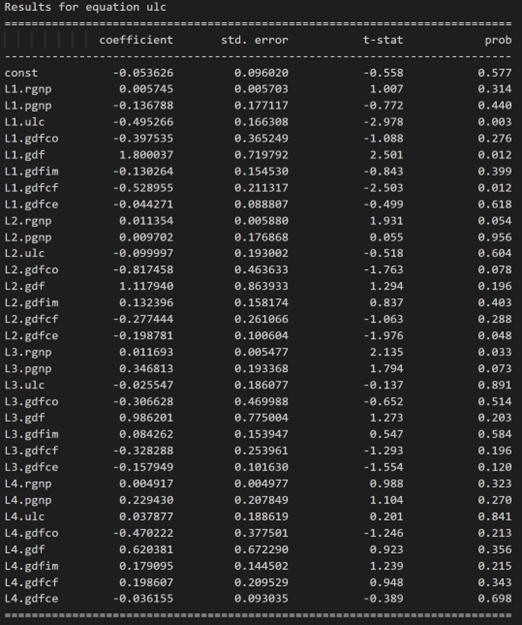
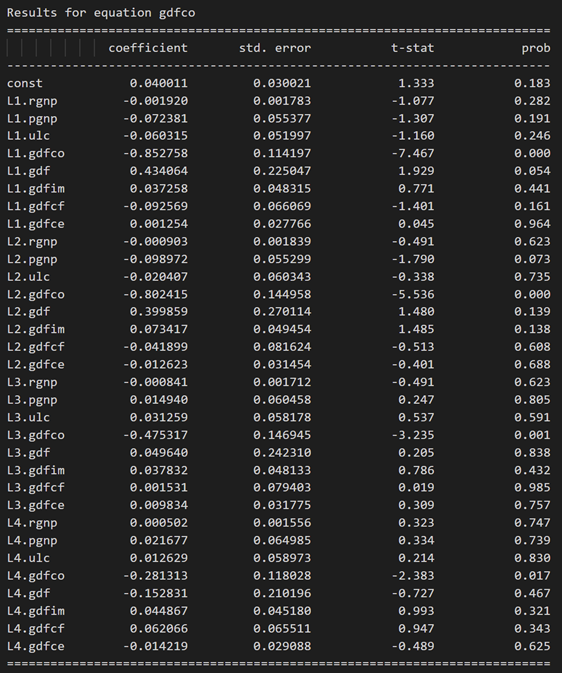
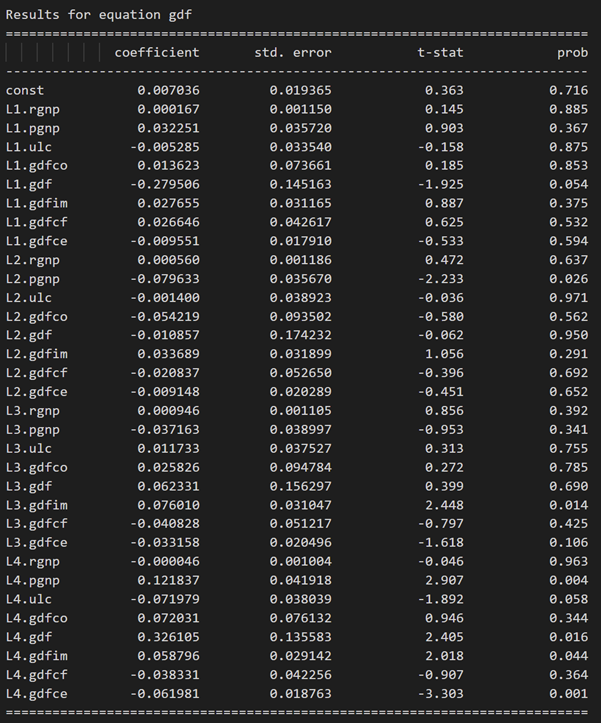
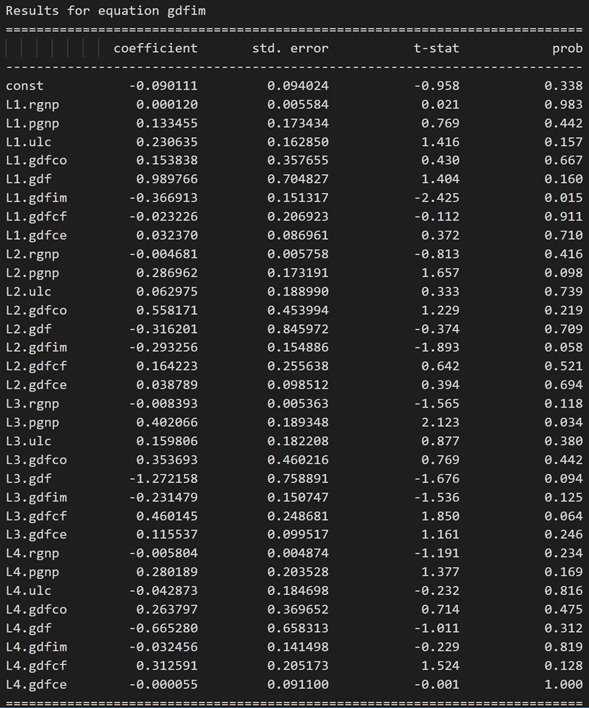
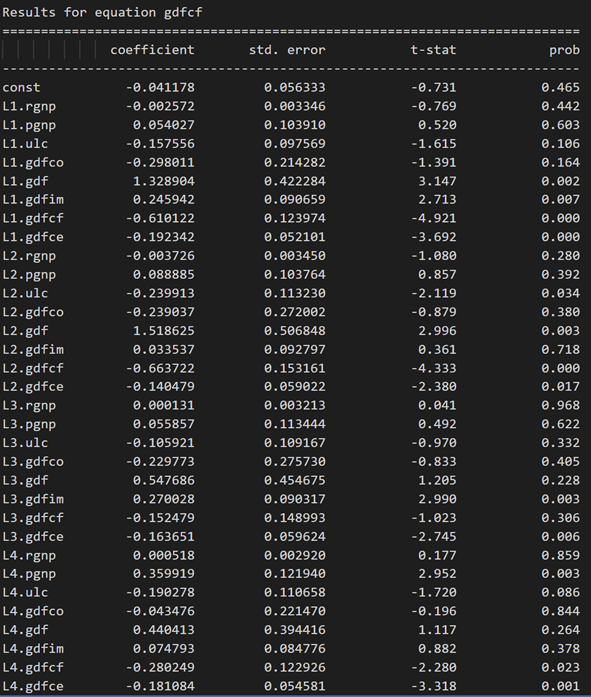
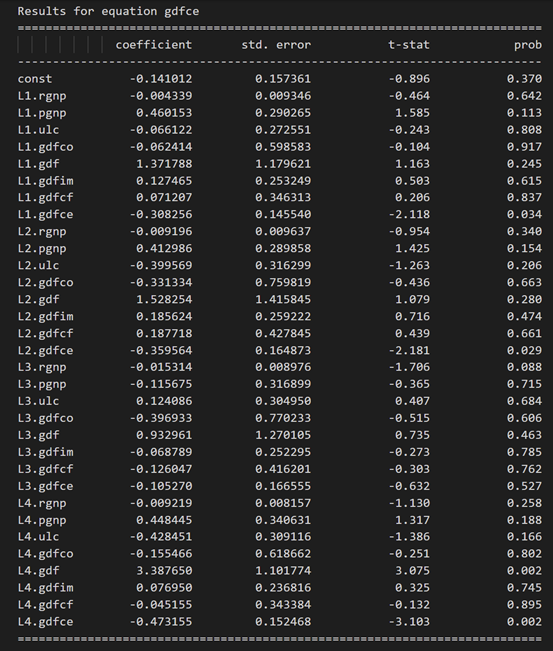
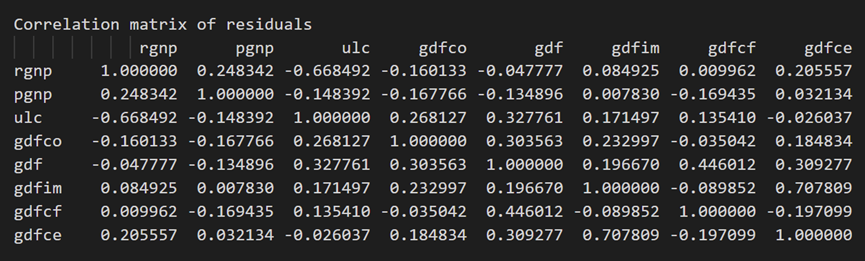
3.10 ダービン ワトソン統計を使用した残差 (誤差) の系列相関の調査

残差の系列相関は、残差に残っているパターン (エラー) をチェックするために使用されます。

これは私たちにとって何を意味するのでしょうか?

残差に相関関係がある場合でも、時系列にはモデルによって説明されるパターンがいくつかあります。この場合の典型的な行動方針は、モデルの次数を上げるか、システムにより多くの予測子を導入するか、時系列をモデル化する別のアルゴリズムを見つけることです。

したがって、系列相関を調べる目的は、モデルが時系列の分散とパターンを適切に説明していることを確認することです。

さて、本題に戻ります。

エラーの系列相関を調べる一般的な方法は、ダービン ワトソン統計を使用して測定することです。

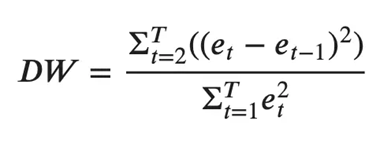
この統計の値は、0 から 4 の間で変動します。値が 2 に近づくほど、有意な系列相関はありません。0 に近いほど系列相関は正であり、4 に近いほど系列相関は負です。

from statsmodels.stats.stattools import durbin_watson
out = durbin_watson(model_fitted.resid)

for col, val in zip(df.columns, out):
    print((col), ':', round(val, 2))

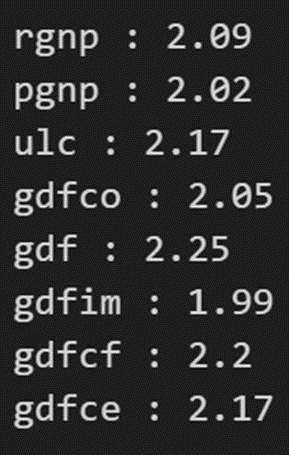
系列相関は良好のようです。予想に移りましょう。

3.11 統計モデルを使用して VAR モデルを予測する方法

予測を行うために、VAR モデルはラグ オーダー数までの過去のデータの観測を想定しています。

これは、VAR モデルの用語が基本的にデータセット内のさまざまな時系列のラグであるため、モデルで使用されるラグの順序で示される数の前の値を与える必要があるためです。

# Get the lag order
lag_order = model_fitted.k_ar
print(lag_order)  #> 4

# Input data for forecasting
forecast_input = df_differenced.values[-lag_order:]
forecast_input

予測してみましょう:

# Forecast
fc = model_fitted.forecast(y=forecast_input, steps=nobs)
df_forecast = pd.DataFrame(fc, index=df.index[-nobs:], columns=df.columns + '_2d')
df_forecast

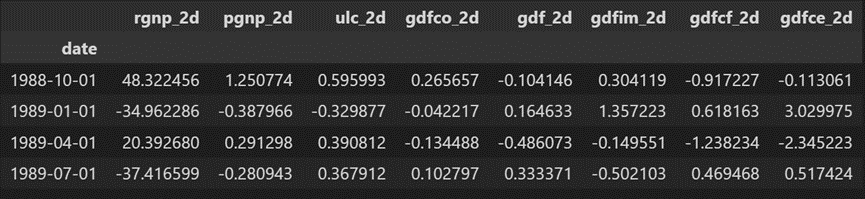
予測が生成されますが、それはモデルによって使用されるトレーニング データのスケールです。そのため、元のスケールに戻すには、元の入力データと同じ回数だけ差分を取る必要があります。

この場合は2回です。

3.12 真の予測を得るための変換の反転

def invert_transformation(df_train, df_forecast, second_diff=False):
    df_fc = df_forecast.copy()
    columns = df_train.columns
    for col in columns:        
        # Roll back 2nd Diff
        if second_diff:
            df_fc[str(col)+'_1d'] = (df_train[col].iloc[-1]-df_train[col].iloc[-2]) + df_fc[str(col)+'_2d'].cumsum()
        # Roll back 1st Diff
        df_fc[str(col)+'_forecast'] = df_train[col].iloc[-1] + df_fc[str(col)+'_1d'].cumsum()
    return df_fc

df_results = invert_transformation(df_train, df_forecast, second_diff=True)        
df_results.loc[:, ['rgnp_forecast', 'pgnp_forecast', 'ulc_forecast', 'gdfco_forecast',
                   'gdf_forecast', 'gdfim_forecast', 'gdfcf_forecast', 'gdfce_forecast']]

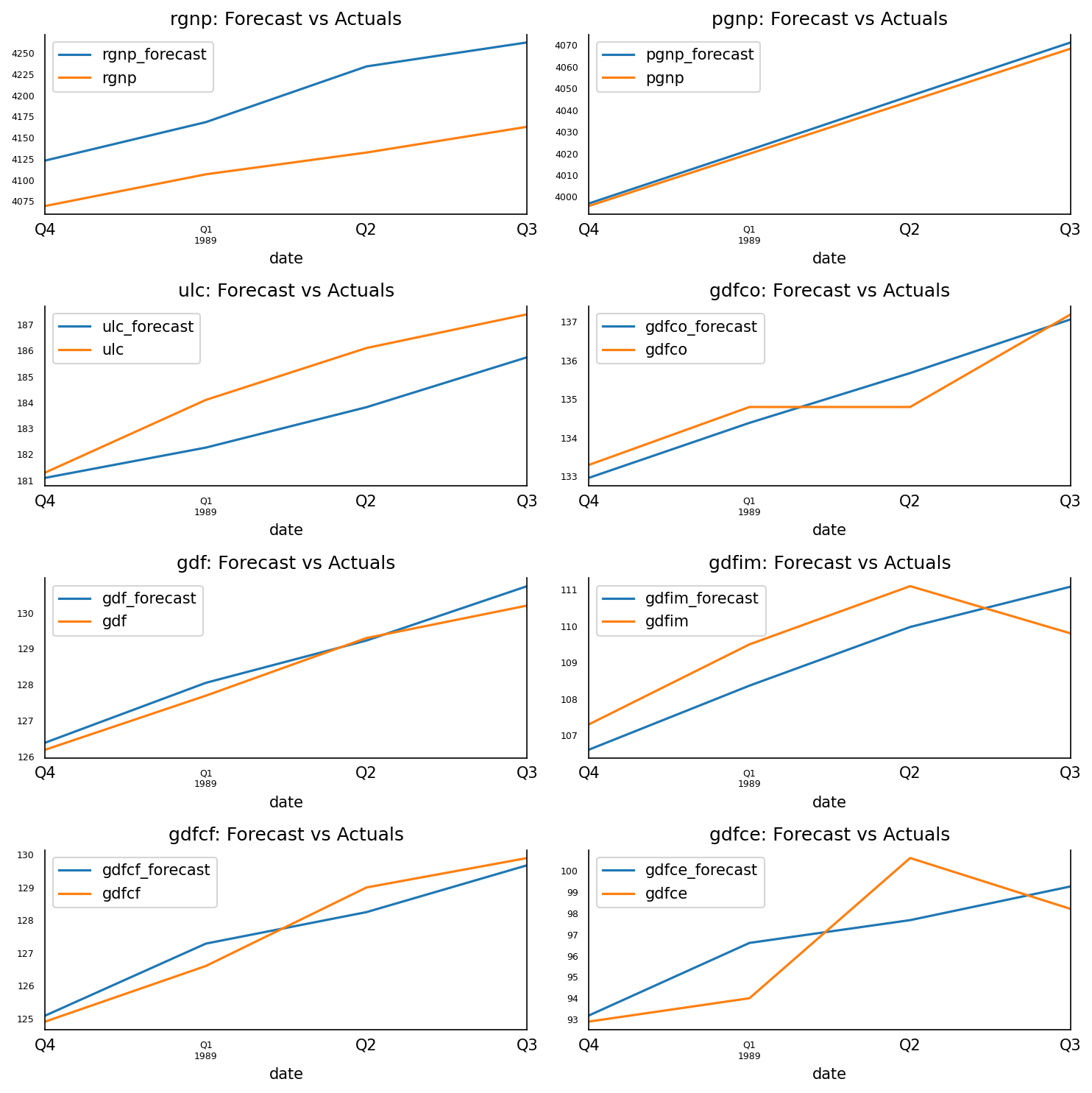
予測は元のサイズに戻ります。テストデータの実際の値に対して予測値をプロットしてみましょう。

3.13 予測対実際のグラフ

fig, axes = plt.subplots(nrows=int(len(df.columns)/2), ncols=2, dpi=150, figsize=(10,10))
for i, (col,ax) in enumerate(zip(df.columns, axes.flatten())):
    df_results[col+'_forecast'].plot(legend=True, ax=ax).autoscale(axis='x',tight=True)
    df_test[col][-nobs:].plot(legend=True, ax=ax);
    ax.set_title(col + ": Forecast vs Actuals")
    ax.xaxis.set_ticks_position('none')
    ax.yaxis.set_ticks_position('none')
    ax.spines["top"].set_alpha(0)
    ax.tick_params(labelsize=6)

plt.tight_layout()

3.14 予測の評価

予測を評価するために、MAPE、ME、MAE、MPE、RMSE、corr、および minmax という包括的なメトリック セットを計算してみましょう。

from statsmodels.tsa.stattools import acf
def forecast_accuracy(forecast, actual):
    mape = np.mean(np.abs(forecast - actual)/np.abs(actual))  # MAPE
    me = np.mean(forecast - actual)             # ME
    mae = np.mean(np.abs(forecast - actual))    # MAE
    mpe = np.mean((forecast - actual)/actual)   # MPE
    rmse = np.mean((forecast - actual)**2)**.5  # RMSE
    corr = np.corrcoef(forecast, actual)[0,1]   # corr
    mins = np.amin(np.hstack([forecast[:,None], 
                              actual[:,None]]), axis=1)
    maxs = np.amax(np.hstack([forecast[:,None], 
                              actual[:,None]]), axis=1)
    minmax = 1 - np.mean(mins/maxs)             # minmax
    return({
    
    'mape':mape, 'me':me, 'mae': mae, 
            'mpe': mpe, 'rmse':rmse, 'corr':corr, 'minmax':minmax})

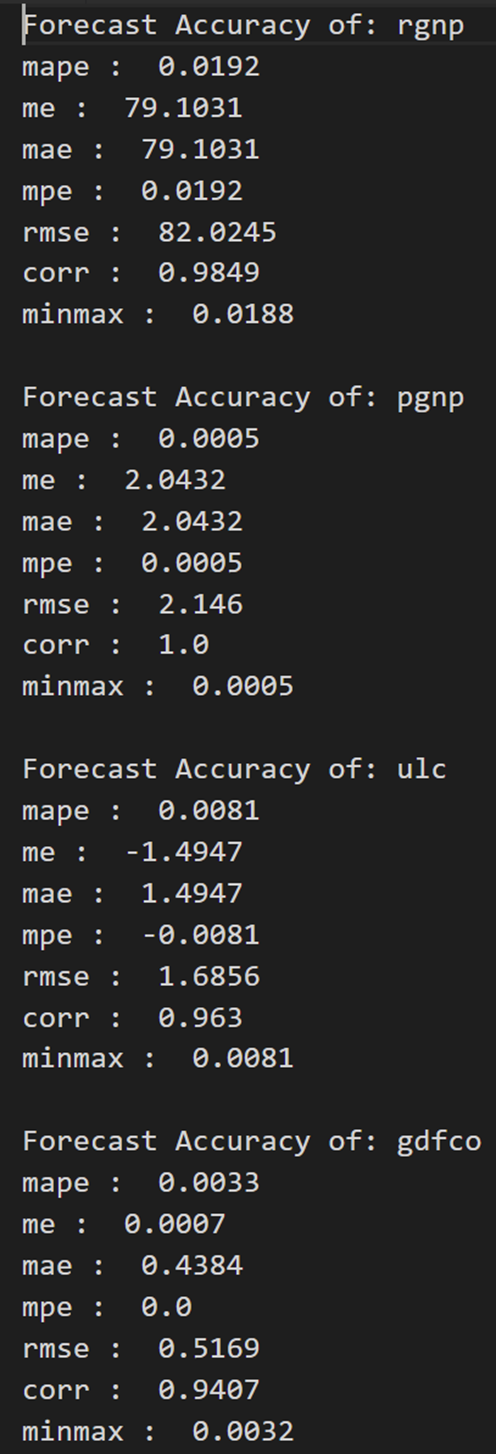
print('Forecast Accuracy of: rgnp')
accuracy_prod = forecast_accuracy(df_results['rgnp_forecast'].values, df_test['rgnp'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

print('\nForecast Accuracy of: pgnp')
accuracy_prod = forecast_accuracy(df_results['pgnp_forecast'].values, df_test['pgnp'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

print('\nForecast Accuracy of: ulc')
accuracy_prod = forecast_accuracy(df_results['ulc_forecast'].values, df_test['ulc'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

print('\nForecast Accuracy of: gdfco')
accuracy_prod = forecast_accuracy(df_results['gdfco_forecast'].values, df_test['gdfco'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

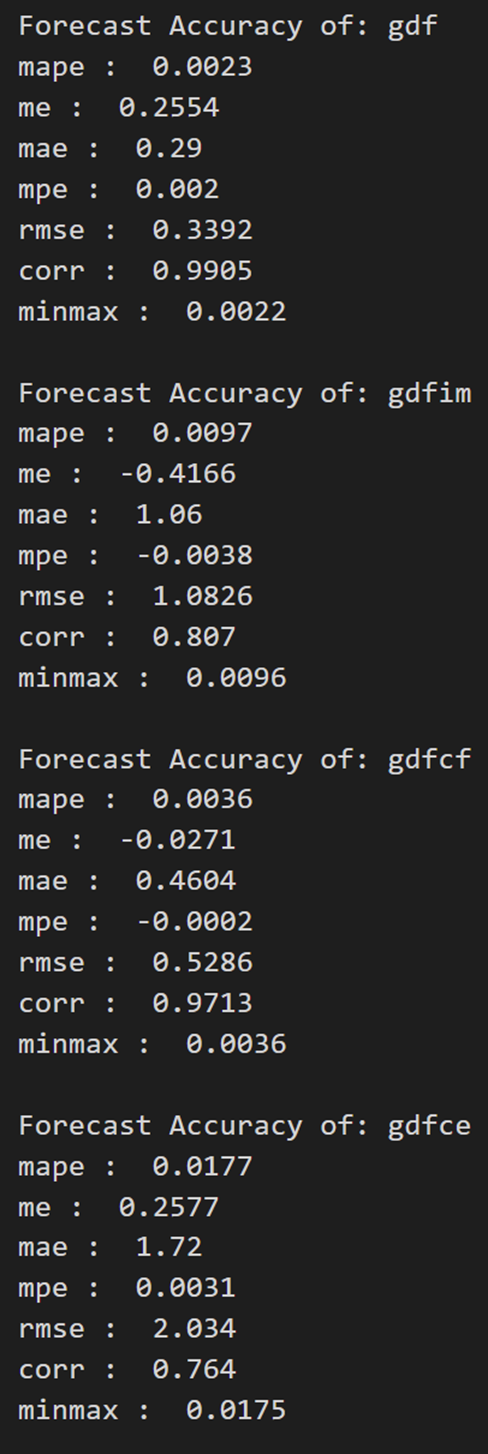
print('\nForecast Accuracy of: gdf')
accuracy_prod = forecast_accuracy(df_results['gdf_forecast'].values, df_test['gdf'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

print('\nForecast Accuracy of: gdfim')
accuracy_prod = forecast_accuracy(df_results['gdfim_forecast'].values, df_test['gdfim'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

print('\nForecast Accuracy of: gdfcf')
accuracy_prod = forecast_accuracy(df_results['gdfcf_forecast'].values, df_test['gdfcf'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))

print('\nForecast Accuracy of: gdfce')
accuracy_prod = forecast_accuracy(df_results['gdfce_forecast'].values, df_test['gdfce'])
for k, v in accuracy_prod.items():
    print(k, ': ', round(v,4))