マインド マッピング:
私の学習目標:
閉区間での連続関数のプロパティを学習したいので、次の手順に従います。
- 最大値、最小値、中間値定理など、閉区間の連続関数の基本的な定義と性質を理解する。
- 閉区間の連続関数には最大値と最小値が必要であることの証明など、閉区間の連続関数のプロパティに関連する基本的な問題を練習します。
- 閉区間上の連続関数の最大値と最小値の存在定理、零点定理、単調性定理などの重要な定理と証明方法をマスターします。
- 三角関数、指数関数、対数関数などの特殊な関数の場合、閉区間での特性をよりよく理解するために、定義域と値の範囲に注意を払う必要があります。
- 閉区間での連続関数の特性についてさらに考えて調べます. いくつかの複雑な問題については, 関連する数学的ツールとテクニックを使ってそれらを分析し解決することができます.
- 最後に、より多くの練習問題と模擬試験を行って、閉区間での連続関数の特性の習熟度と、複雑な問題を処理する能力をテストします。同時に、導関数や積分など、関連する他の数学の知識を組み合わせて学習することで、総合的な数学リテラシーを向上させることもできます。(練習は理論をテストするための最良の方法です)


私の理解
有界性と最大・最小定理は機能科学において比較的重要な概念・定理であり、主な内容は次のとおりです。
- 有界性: 区間内の値の範囲が有限である場合、関数は区間内で有界であると言われます。数学的には、上限と下限を定義することで、関数の有界性を説明できます。
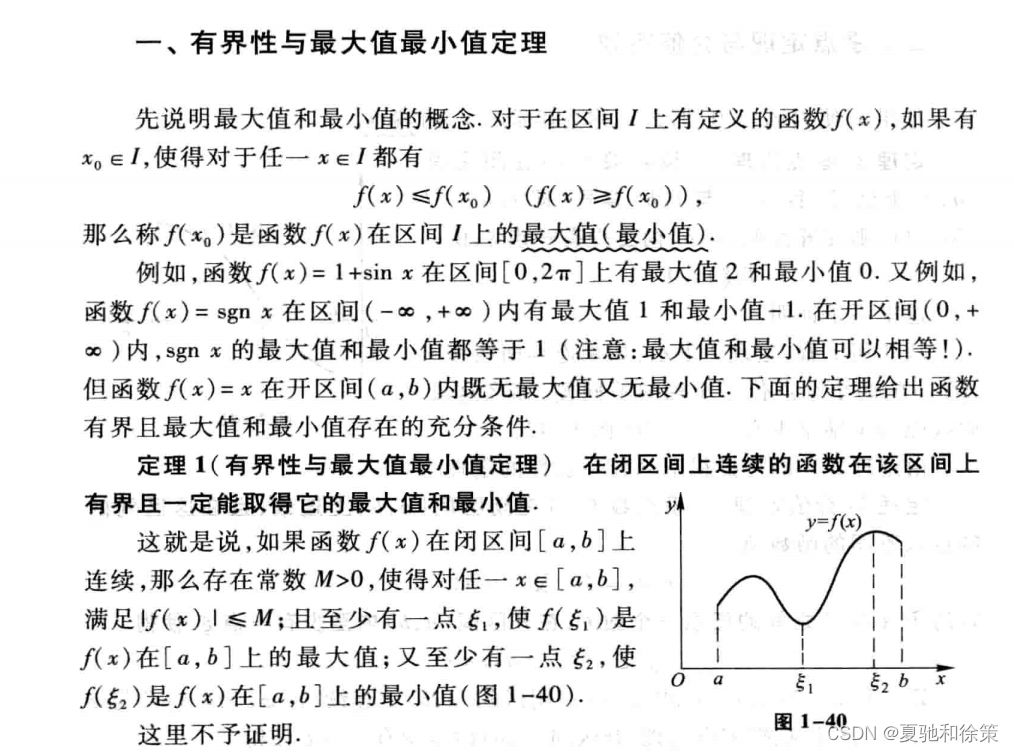
- 最大定理と最小定理: 関数が閉区間で連続である場合、関数は区間に最大値と最小値を持たなければなりません。具体的には、関数 f(x) が閉区間 [a, b] 上で連続である場合、f(x0) ≤ f(x) ≤ f(x1) となるような x0, x1 ∈ [a, b] が存在します。任意の x ∈ [a, b] が成立します。このうち、x0 と x1 を閉区間 [a, b] 上の関数 f(x) の最小点と最大点と呼びます。
- 有界性と最大最小定理を学ぶときは、次の点に注意する必要があります。
- 三角関数、指数関数などの一部の特殊関数については、関数の有界性と最大値と最小値の存在をよりよく理解するために、それらの定義領域と値の範囲の特性に注意を払う必要があります。
- 最大最小定理の証明には、通常、矛盾証明や平均値定理などの方法が用いられます。これらの証明方法を使用する場合、証明プロセスの詳細と論理的推論に注意を払う必要があります。
- 実際のアプリケーションでは、関数の最大点を見つけたり、関数が特定の区間で解を持つかどうかを判断したりするために、有界性と最大および最小定理がよく使用されます。したがって、これらの概念と定理を学ぶときは、理論と実際の応用の組み合わせに注意を払う必要があります。
 私の理解:
私の理解:
ゼロ点定理と中間値定理は、機能科学における 2 つの重要な定理であり、主に次の側面について説明します。
- ゼロ点定理: 連続関数 f(x) が区間 [a, b] に異なる符号の 2 つの実数 f(a) と f(b) を持つ場合、(a, b には少なくとも 1 つの点 x0 が存在します。 ) f (x0) = 0 となります。つまり、連続関数には、区間内の反対符号の端点の間に少なくとも 1 つのゼロがあります。
- 中間値定理: 連続関数 f(x) が区間 [a, b] で 2 つの異なる関数値 f(a) と f(b) を取得する場合、f(a) と f(b) の間の任意の値について) 実数 c の間に点 x0 ∈ [a, b] があり、f(x0) = c となります。つまり、連続関数には、区間内の任意の 2 つの関数値の間に少なくとも 1 つの関数値があります。
- 零点定理と中間値定理を学ぶときは、次の点に注意する必要があります。
- これら 2 つの定理の前提条件は、関数 f(x) が区間 [a, b] で連続であるため、これらの定理を使用する場合、関数が連続性を満たすかどうかを判断する必要があります。(エラーを起こしやすい)
- 零点定理や中間値定理を証明するときは、矛盾による証明や中間値定理(基本的な考え方)などの方法が使えます。証明の過程では、証明の詳細と論理的推論に注意を払う必要があります。
- ゼロ点定理と中間値定理は、方程式の根を見つける、存在を証明するなど、多くの実際的な問題に適用できます。適用する際には、問題の具体的な状況に応じて適切な定理を選択する必要があり、条件の制約や推論の厳密さに注意する必要があります。
- つまり、ゼロ点定理と中間値定理を学ぶことは、機能科学の比較的重要な部分であり、数学の問題を解決し理解する能力を向上させるのに非常に役立ちます。





私の理解:
- 均一連続性は、機能的連続性のより強力な形式です。関数 f(x) が定義域 D 上で連続であり、任意の正の実数 ε に対して正の実数 δ が存在し、x1、x2 ∈ D および |x1 - x2| < δ の場合、| が存在する場合f (x1) - f(x2)| < ε が成り立つ場合、関数 f(x) は D 上で無矛盾かつ連続的であると言われます。
- 通常の連続性と比較して、一貫した連続性にはより厳しい要件があります。つまり、関数の変化は、任意の点で連続性を満たすだけでなく、定義のドメイン全体で、突然の「ジャンプ」なしである程度の滑らかさを維持します。
- 一貫した連続性を学習するときは、次の点に注意する必要があります。
- 一貫した連続性は機能的連続性のより強力な形式ですが、すべての連続的な機能が一貫して連続しているわけではないため、機能の特定のプロパティに注意して、一貫した連続性があるかどうかを判断する必要があります。
- 関数が一貫した連続性を持つことを証明する場合、定義に従って修飾δを与えると同時に、推論プロセスの厳密さと合理性に注意を払う必要があります。
- 一貫した連続性は、数学的分析、微積分、常微分方程式などの分野など、実際の問題で非常に重要な用途があり、問題の理解と解決に非常に役立ちます。
応用:
閉区間の連続関数は、数学的分析で広く使用されています。これらのアプリケーションのいくつかを次に示します。
- 存在証明: 中間値定理、最大値定理、最小値定理などを通じて、数学や物理学で広く使用されている特定の物理量または関数値が特定の条件下で存在することを証明できます。
- 方程式と方程式を解く: ゼロ点定理を通じて、連続関数方程式または閉区間の方程式の解を得ることができます。
- 近似問題: 近似定理により、閉区間上の連続関数を点ごとに多項式に近似することができ、数値計算と解析が容易になります。
- 最適化問題: 最大値最小値定理を使用して、閉区間上の連続関数の最大値と最小値を取得して、さまざまな最適化問題を解くことができます。
- 物理的な問題: 多くの物理的な問題は、運動学の問題、波動の問題など、閉区間で連続関数モデルを確立することによって解決できます。

